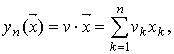УДК: 616.8/831.2-072

СТАТИСТИЧЕСКИЙ КРИТЕРИЙ ОБНАРУЖЕНИЯ ВЫЗВАННЫХ ПОТЕНЦИАЛОВ

Ф. Н. Григорьев, Н. А. Кузнецов

Институт радиотехники и электроники им. В.А. Котельникова РАН

Получена 25 марта 2013 г.

Аннотация. Для обнаружения вызванных потенциалов (ВП) в сигналах электроэнцефалограмм предложено использовать критерий Неймана-Пирсона. Синтезирован оптимальный алгоритм обнаружения ВП. Проведено моделирование, подтверждающее его работоспособность. [1]

Ключевые слова: вызванные потенциалы, электроэнцефалография, статистический критерий Неймана-Пирсона, корреляционные функции, моделирование.

Abstract: The criterion of von Neumann-Pearson is proposed for the detection of evoked potentials (EP) in the electroencephalogram (EEG) signals. The optimal algorithm for the detection of the EP was synthesized. The modeling confirmed its efficiency.

Key words: evoked potentials, electroencephalography, Neyman-Pearson statistical criterion, correlation functions, modeling.

 

Введение

Метод вызванных потенциалов, в дальнейшем ВП, давно внедрен в клиническую практику, и в последующем его роль будет только возрастать. Метод используется, преимущественно, в медицине для объективного тестирования различных сенсорных систем: зрения, слуха, соматической чувствительности, для получения данных о локализации органических церебральных поражений, для изучения состояния проводящих путей мозга и реактивности различных церебральных систем при патологических процессах, действия наркоза и лекарственных препаратов. Помимо медицинских целей метод ВП используется в близких дисциплинах – нейролингвистике, в психологических исследованиях восприятия, распознавания образов, уровней функциональной активности мозга [1-4].

Успехи экспериментальной и теоретической неврологии с использованием ВП давно привлекали внимание клинической нейрофизиологии, однако на пути стандартного использования метода стояли существенные трудности. При регистрации ВП от интактных покровов головы дополнительно регистрируется электрическая активность в виде электроэнцефалограмм (ЭЭГ), электромиограмм, аппаратурных шумов и любых артефактов, ее амплитуда в норме достигает 100 мкВ, а при патологии – 200, 500 и даже 1000 мкВ. На этом фоне сигнал ВП, не превышающий обычно 15мкВ, выделять затруднительно. Зрительные ВП имеют амплитуду до 10мкВ, соматосенсорные ВП при стимуляции нервов – около 2мкВ, некоторые компоненты стволовых ВП – до 0,5мкВ. Отношение сигнала ВП к спонтанной ЭЭГ для зрительных ВП составляет 1/5, для соматосенсорных - 1/25, а для стволовых компонентов менее 1/100 [1]. Поэтому практически ни один из сигналов ВП нельзя видеть на обычной записи ЭЭГ. Для того, чтобы их увидеть и зарегистрировать, нужно, чтобы это отношение составляло хотя бы 2/1.

Кроме того, ВП генерируется несколькими типами активности с различными временными и, возможно, пространственными характеристиками. В итоге образуется ВП сложной волновой конфигурации.

Выделение повторяющегося сигнала на фоне шума, в случаях, когда известны моменты появления самого сигнала или связанного с ним вспомогательного сигнала, содержит два аспекта: обнаружение сигнала и выделение сигнала с наименьшей ошибкой. Для решения этой задачи была предложена методика синхронного накопления. Суть ее заключается в том, что участки электрической активности фиксированной длительности, следующие за подачей стимула, так называемой эпохи анализа, последовательно суммируются. Начало анализируемых отрезков должно совпадать во времени с моментом подачи стимула. При этом колебания ВП, возникающие синхронно со стимулом, накапливаются синфазно и дают прирост амплитуды пропорционально  – числу суммирований. Спонтанная же активность суммируется несинхронно, в результате прирост ее амплитуды происходит пропорционально , и в результате ВП проявляется отчетливей.

Основным критерием качества выделения ВП является отношение сигнал/шум, который прямо пропорционален . Диапазон применяемого числа усреднений для выделения ответов мозга весьма разнообразен: для одних достаточно нескольких суммирований, чтобы обнаружить ответ, для других, например, стволовых и ряда коротколатентных соматосенсорных, порядка нескольких тысяч [1].

Несмотря на то, что синхронное усреднение – мощный метод, позволяющий выделить сигнал практически при любом соотношении уровня сигнал/шум, он обладает рядом серьезных недостатков, из которых главный – необходимость подачи большого числа стимулов. Это снижает физиологичность процедуры. При каждой подаче ВП мозг реагирует активно [5], изменяя свой ответ на один и тот же потенциал. В результате возникает эффект привыкания и другие связанные процессы в ЦНС. Кроме того, есть стимулы, которые по своей природе не могут подаваться многократно, например, болевые, обонятельные и вкусовые.

В этом случае актуальной становится задача определения наличия ВП у обследуемого пациента при возможно меньшем числе усреднений. Тогда, в случае отсутствия ВП у пациента, становится возможным отменить его дальнейшее обследование. Если же ВП обнаружен, то можно продолжить обследование для уточнения формы ВП. Решению этой задачи и посвящена данная работа.

Постановка задачи

В настоящее время имеются надежные данные для конкретных ВП как по продолжительности во времени, так и по изменению величины сигнала в течение эпохи анализа. Врач наблюдает или регистрирует на приборе реализацию случайного процесса, которая может представлять сумму сигналов ВП и помехи в виде сигнала ЭЭГ, либо только сигнал ЭЭГ. Его задача состоит в том, чтобы, используя заранее выработанное правило, вынести решение о наличии или отсутствии сигнала ВП в данной реализации. Подобные задачи обнаружения сигнала на фоне помех относятся к классу задач проверки статистических гипотез.

Обозначим через  реализацию случайного процесса , наблюдаемую на интервале эпохи анализа . Выдвигается гипотеза  о том, что  – случайная помеха, а именно, сигнал ЭЭГ без ВП, являющаяся коррелированным гауссовским процессом с нулевым средним, против альтернативной гипотезы , что , где  – полезный сигнал ВП.  предполагается детерминированным.

На основании определенного правила, оптимального по некоторому критерию, необходимо принять решение  о наличии ВП (гипотезу ) или решение  об отсутствии ВП (гипотезу ).

Наблюдения реализации  производятся в дискретные моменты времени с шагом временной дискретизации . Эпоха анализа равна  измерениям, что соответствует с реального времени.

В этом случае наблюдение можно представить выборкой заданного  размера

                        

Элементы выборки – гауссовские случайные величины, средние значения которых

             

По графикам ВП, взятым, например, из [1], получаем значения    с временным шагом  Значения , в отсутствие , получаем из записи соответствующей ЭЭГ вычитанием среднего значения

Корреляционная матрица K для выборки  заменяется ее оценкой и предполагается одинаковой при гипотезах  и

Функции правдоподобия выборки  записываются в виде

 

где  – вектор значений вынужденного потенциала в моменты дискретизации.

За критерий качества алгоритма принятия решения выбираем критерий Неймана-Пирсона. Как и в общей теории проверки гипотезы  против альтернативы , рассмотрим ошибки двух видов:

– первого рода, когда принимается решение о наличии ВП, а в действительности его нет, и

– второго рода, когда принимается решение, что ВП нет, а в действительности он присутствует.

Вероятности -ошибки первого рода и -ошибки второго рода удовлетворяют выражениям

   

Вероятность правильного обнаружения ВП составляет

Оптимальный по критерию Неймана-Пирсона алгоритм обнаружения обеспечивает максимум вероятности правильного обнаружения сигнала ВП при заданной вероятности -ошибки первого рода.

Синтез оптимального алгоритма обнаружения ВП

Как следует из общей теории проверки статистических гипотез, оптимальный по критерию Неймана-Пирсона алгоритм принятия решения предписывает сравнение с порогом достаточной статистики логарифма отношения правдоподобия.

В рассматриваемом случае логарифм отношения правдоподобия записывается в виде

или

Поскольку корреляционная матрица помехи и детерминированный сигнал ВП в рассматриваемом случае представляют известные данные, то достаточной статистикой является также

Введя вектор-строку  можно представить статистику в виде скалярного произведения

(1)                                     

 

т.е. линейной комбинацией гауссовских величин.

Когда сигнала ВП нет, то математическое ожидание и дисперсия статистики запишутся в виде

(2)                           

(3)         

Используя выражения (1) - (3), находим уравнение, определяющее порог критерия С при заданной вероятности ошибки первого рода α

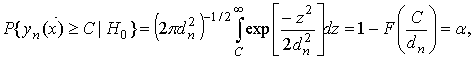         или

 

(4)                                                

где  – квантиль нормального распределения, удовлетворяющая условию  Например, для  

Заметим, что величина  которую можно назвать обобщенным отношением мощностей сигнал – помеха, всегда положительна, поскольку корреляционная матрица  положительно определенная.

Сформулируем оптимальный по критерию Неймана-Пирсона алгоритм обнаружения ВП: принимается решение  о наличии ВП, если

(5)                                  

 

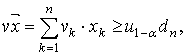
и, в противном случае, решение   о том, что ВП нет.

Найдем зависимость вероятности правильного обнаружения ВП от вероятности ошибки первого рода  для алгоритма (5). Поскольку статистика (1) при наличии ВП тоже представляет гауссовскую случайную величину, то для определения вероятности правильного обнаружения ВП достаточно найти математическое ожидание и дисперсию этой случайной величины при альтернативе  Из (1) следует

(6)                  

(7)                  

Используя (6), (7) и (4), находим вероятность правильного обнаружения ВП

 или

 

(8)                                            

Выражение (8) определяет вероятность  правильного обнаружения ВП при заданной  – вероятности ошибки первого рода без суммирования сигналов.

Возникает вопрос, как увеличить, если нужно, вероятность  до желаемого значения, не увеличивая при этом  – вероятность ошибки первого рода.

Для заданных вероятностей  и  ошибок первого и второго рода из выражения (8), с учетом свойства квантилей нормального распределения, следует, что значение  должно быть не меньше значения  удовлетворяющего условию

(9)                                            

Как показано ниже в разделе «Моделирование. Независимость выборок», время корреляции сигнала ЭЭГ меньше 50mc, что не превышает продолжительности эпохи анализа .

Отсюда следует, что при  суммирований сигналов для обнаружения ВП суммируются некоррелированные сигналы и , входящее в (3), изменяется пропорционально  Величина же  при этом пропорциональна  Поэтому число суммирований сигналов для обнаружения ВП с вероятностями ошибок первого и второго рода, не превышающими, соответственно, заданных значений  и , равно  где  – наименьшее целое число, удовлетворяющее неравенству  Здесь  соответствует

Таким образом, при числе суммирований сигналов  значение , а значение  определяет порог критерия при заданной вероятности ошибки первого рода . При выбранном пороге  вероятность правильного обнаружения ВП определяется из выражения

Также возможна альтернатива обеспечить равенство вероятностей ошибок первого и второго рода

В этом случае значение порога составит

Моделирование.  Правило обнаружения ВП

В качестве конкретного примера, иллюстрирующего полученные результаты, приведены результаты моделирования зрительных ВП здорового человека в ответ на вспышку света при бинокулярной стимуляции. Активным являлся электрод 02 согласно международной схеме 10-20%. В качестве референтного использовался ушной электрод А2. Шаг временной дискретизации сигнала составлял   

На рис. 1 представлены значения ВП в mkV в пятидесяти моментах времени, составивших эпоху анализа. Для сравнения на рис. 2 представлен один из отрезков ЭЭГ в mkV без наложения ВП. Оценка корреляционной функции представлена на рис. 3.

 

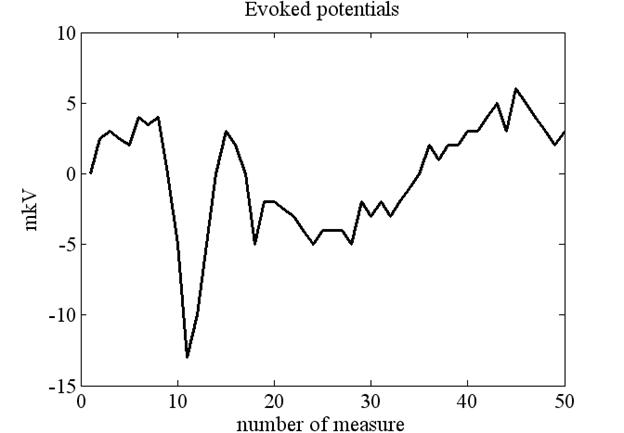
Рис. 1 Значения зрительных ВП, mkV, в пятидесяти моментах

времени эпохи анализа

 

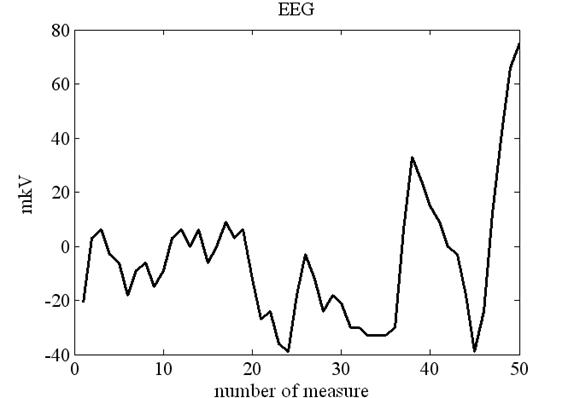
Рис. 2 Значения ЭЭГ, mkV, в пятидесяти моментах времени без наложения зрительных ВП

 

      

Рис. 3 Оценка корреляционной функции сигнала ЭЭГ

 

При использовании выражения (3) получено значение  соответствующее принятию решения по одной выборке без суммирования. Принимая значения вероятности ошибок первого и второго рода , в соответствии с (9) получено требуемое значение . Минимальное количество суммирований в этом случае составляет

.

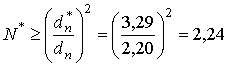Отсюда находится  – число суммирований выборок, удовлетворяющее заданным требованиям к ошибкам первого и второго рода.

Для случая суммирования трех выборок сигнала . Порог .

         По формуле (1) для ста различных участков ЭЭГ без ВП и ста сумм ЭЭГ и ВП найдены значения . Результаты представлены на рис. 4. Горизонтальная прямая соответствует порогу . Верхняя пунктирная кривая соединяет сто точек , соответствующих различным участкам ЭЭГ с наложением ВП. Нижняя сплошная кривая соединяет сто точек , соответствующих различным участкам ЭЭГ без ВП.

Из представленных данных видно, что рассмотренный критерий хорошо разделяет ЭЭГ с ВП и ЭЭГ без ВП.  Отсутствие ошибок первого и второго рода в данном случае связано с конечным набором вариантов (двести). Кроме того, , что соответствует меньшей вероятности ошибок , чем изначально заданное значение . 

   

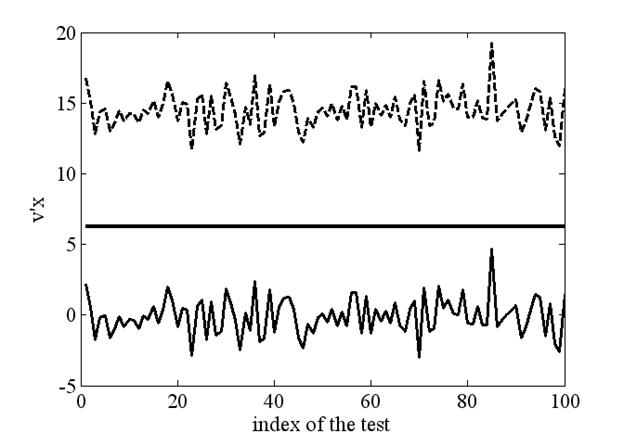
Рис. 4 Результаты моделирования: наличие  (---) и отсутствие ВП (–) по отношению к пороговому значению (прямая линия)

 

Моделирование.  Независимость выборок

Из графика оценки корреляционной функции (рис. 3) следует, что значение выборочного нормированного коэффициента корреляции , при ,   Определим значимость коэффициента корреляции  т.е. проверим гипотезу  На уровне значимости  критическая область этого критерия определяется неравенством [6]

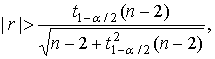
 – квантиль распределения Стьюдента от  степеней свободы. При  получаем критическую область  Поскольку 0,07<0,18, то нет оснований отвергать гипотезу  Исходя из вышеизложенного следует считать, что отсчеты ЭЭГ имеют значения коэффициента корреляции  при значениях корреляционной функции по модулю, меньших 160.

Использование полученных результатов практикующими специалистами

Поскольку для определения ВП используются разные приборы, измерения производятся в разных диапазонах и предъявляются разнящиеся требования к выделению конкретного ВП, то написать единую методику для использования разработанного метода с учетом всего многообразия требований не имеет смысла.

Укажем лишь последовательность стандартных шагов в общем пути решения задачи обнаружения ВП врачом-специалистом на конкретном примере выявления зрительных ВП в ответ на вспышку света при бинокулярной стимуляции.

Для определения наличия конкретного ВП у пациента по известным литературным данным определяется:

1)    Продолжительность эпохи анализа  и количество измерений сигналов ЭЭГ за эпоху с учетом шага временной дискретизации между измерениями . Например,   ;

2)    Определяется значение ВП  при каждом измерении сигнала ЭЭГ в течение эпохи анализа (в рассматриваемом примере в 51 значении времени анализа);

3)    По записи ЭЭГ, в которой необходимо определить наличие ВП, находим оценку корреляционной матрицы  размера  с временным шагом  в соответствии с пунктом 1;

4)    В соответствии с (3) определяется значение

5)    Для заданных вероятностей ошибок первого и второго рода –  и , определяется наименьшее допустимое значение

                   где  и  – квантили нормального распределения;    

6)    Определяется наименьшее число суммирований сигнала для обнаружения ВП как наименьшее целое число, удовлетворяющее неравенству

7)    Для найденного  определяется значение порога

8)    Определяется значение  где  является  раз суммированным сигналом в течение эпохи анализа;

9)    Если  то принимается решение о наличии ВП, и, в противном случае, решение о том, что ВП отсутствует;

10)                      Вероятность  правильного обнаружения ВП определяется из выражения

Выводы

Для обнаружения вызванных потенциалов в сигналах ЭЭГ предложено использовать статистический критерий Неймана-Пирсона.

Синтезирован оптимальный алгоритм обнаружения вызванных потенциалов на фоне сильных шумов.

Проведено моделирование, подтверждающее на конкретных примерах надежное обнаружение вызванных потенциалов с помощью синтезированного алгоритма.

Показано, что для обнаружения вызванных потенциалов в сигналах ЭЭГ требуется 3-5 суммирований выборок из ЭЭГ, что существенно меньше обычно используемых 50-100 [1].

Разработаны методики выявления вызванных потенциалов для практикующих в клиниках специалистов.

 

Литература

1.     Нейрофизиологические исследования в клинике. Ред.  Щекутьев Г.А. М.: Антидор, 2001. – 232 с.

2.     Иванов-Муромский К.А., Заславский С.Я Применение ЭВМ для анализа электрограмм мозга. Киев: Наукова Думка, 1968. – 144с.

3.     Гнездицкий В.В. Обратная задача ЭЭГ и клиническая электроэнцефалография (картирование и локализация источников электрической активности мозга). – М.: МЕДпресс-информ, 2004. – 624 с.

4.     И. А. Секерина Метод вызванных потенциалов мозга в американской психолингвистике и его использование при решении проблемы порядка слов в русском языке. Труды международной конференции Диалог'2002 "Компьютерная лингвистика и интеллектуальные технологии". М.: Наука, 2002, http://www.dialog-21.ru/digest/archive/2002/

5.     Кандель Э. В поисках памяти. Возникновение новой науки о человеческой психике. М.: Астрель: Corpus, 2012. – 736c.

6.     Крамер Г. Математические методы статистики. М.-Ижевск: НИЦ Регулярная и хаотическая динамика, 2003. – 648с.

---

[1] Работа выполнена при финансовой поддержке гранта РФФИ 13-01-00885