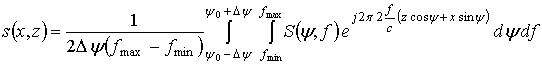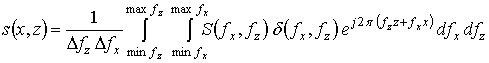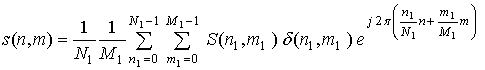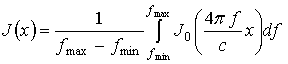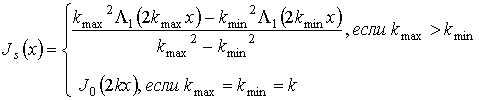УДК 621.396

К описанию функции неопределенности сигнала при инверсном синтезировании двумерных радиолокационных изображений объектов

 

О. Б. Гузенко, С. И. Моряков, С. М. Нестеров, И. А. Скородумов

Центральный научно-исследовательской институт Войск ВКО Минобороны России

Статья получена 12 марта 2015 г.

 

Аннотация.  В работе предложено описание функции неопределенности сигнала при инверсном синтезировании двумерных радиолокационных изображений объектов методами прямого интегрирования и «пространственных частот». Получены точная и приближенная оценки потенциального разрешения двумерных изображений объектов и уровня цифрового фона в некоторых практически интересных случаях, в том числе, при зондировании на фиксированной частоте, вкруговую и в условиях сверхширокополосной локации.

Ключевые слова: эффективная площадь рассеяния, инверсное синтезирование апертуры, радиолокационные изображения.

Abstract: The paper proposes a description of the ambiguity function of the signal by objects ISAR imaging using direct integration methods and techniques of Fourier transformations. In some cases an exact and approximate estimation of ISAR image resolution and level of digital background are obtained, including single-frequency and circular imaging.

Key words: radar cross section, inverse synthetic aperture, radar images.

 

Современные радиолокационные системы и средства, использующие широкополосные когерентные приемники и эффективные методы цифровой обработки сигналов [1-3], обеспечивают новое качество получаемой радиолокационной информации. В частности, позволяют формировать инверсно синтезируемые двумерные радиолокационные изображения (РЛИ) аэродинамических, баллистических и космических объектов с высоким разрешением (рис.1).

 

Рис.1. РЛИ Space Shuttle, полученное на РЛС TIRA [4]

Для эффективного использования РЛИ при решении практических задач необходимо получать изображения с потенциально лучшей разрешающей способностью и минимальным уровнем цифрового фона, для чего требуется обеспечить описание функции неопределенности радиолокационного сигнала при инверсном синтезировании для любых диапазонов изменения частот зондирующего сигнала и углов локации. Известные из литературы описания функции неопределенности радиолокационного сигнала при инверсном синтезировании двумерных РЛИ объектов [5-8] посвящены частным случаям зондирования на фиксированной частоте, в узкой полосе частот, узком секторе углов локации или, напротив, локации вкруговую. Кроме того, существуют неточности в описании функции неопределенности [8], вытекающие из не учтенной кривизны области определения сигнала при его свертке.

Цель работы – обеспечить возможность получения функции неопределенности радиолокационного сигнала при инверсном синтезировании двумерных РЛИ объектов для любых диапазонов изменения частот зондирующего сигнала и углов локации, а также оценить потенциальное разрешение получаемых изображений и уровень цифрового фона.

Рассмотрим зондирование вращающегося объекта импульсным периодическим сигналом с перестройкой частоты.

При выполнении условий дальней зоны оператор синтезирования двумерного РЛИ объекта под ракурсом , в декартовых координатах дальности и поперечной координаты плоскости локации, имеет вид [5]

, (1)

 

где     - комплексная амплитуда отраженного объектом сигнала в точке с координатами по дальности и  – поперек;

 - комплексная амплитуда отраженного объектом сигнала в координатах угла поворота , изменяющегося от  до , и частоты зондирования  в полосе перестройки от  до .

Вместо прямого интегрирования, трудоемкого в вычислительном отношении, свертку сигнала в область декартова пространства осуществляют с помощью обратного быстрого преобразования Фурье. Для исключения искажений метрики получаемых изображений (из-за имеющейся нелинейной зависимости фазы от угла), перед преобразованием Фурье выполняют интерполяцию сигнала из полярных координат «частота-угол» в прямоугольные координаты так называемых «пространственных частот» [5]  и , формируя билинейную связь исходных и результирующих координат.

Свертка сигнала из области «пространственных частот», с учетом симметрии по  и области определения в виде кругового сектора (рис.2), -

.   (2)

 

где

         ,

.

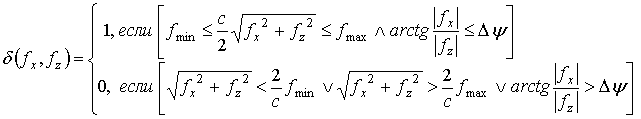
Дискретная форма оператора (2) c учетом выполненной интерполяции сигнала из полярных в прямоугольные координаты имеет вид

,   (3)

 

где    ,

, ,

, , ,

, , ,

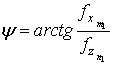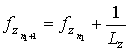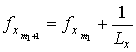,  - задаваемые размеры координатной области.

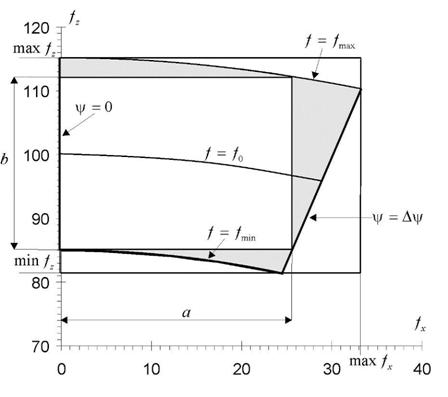
Размеры области определения «пространственных частот» при  (рис.2):

, ,

, .

При

, ,

, .

Рис. 2. Область определения сигнала

Необходимо отметить, что после дискретизации задачи численный результат свертки сигнала по выражениям (1) и (2) в общем случае будет отличаться, поскольку точки прямоугольной сетки не совпадают с точками полярной сетки, а шаги прямоугольной сетки ограничены снизу значениями  и , которыми приближенно оценивается разрешающая способность получаемых изображений в осевых направлениях. Отсюда возникает вопрос о величине различий функции неопределенности при инверсном синтезировании РЛИ объектов по исходному (1) и преобразованному (2) сигналу и о потенциальном разрешении изображений, ответ на который дан ниже.

Запишем функцию неопределенности синтезируемых РЛИ по исходному сигналу в полярных координатах:

,

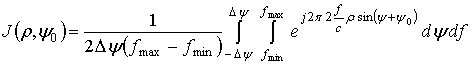где     – радиус-вектор точки,  - угол между радиус-вектором и осью .

Разрешающую способность в любом направлении  определяют в соответствующем сечении этой функции по значению ее модуля на фиксированном уровне – обычно на уровне 0,7 (или квадрата модуля на уровне -3 дБ) [5]. В данной работе значения разрешений будем определять по квадрату модуля функции на уровне -4 дБ, отталкиваясь от того, что известная оценка разрешения по Релею 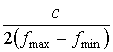 соответствует половине ширины главного лепестка функции  по «нулям» и равна ширине этого лепестка на уровне 0,637 [1], то есть на уровне -4 дБ по мощности.

Потенциально лучшее значение разрешения по поперечной координате (по «азимуту») получим при синтезировании сигнала в секторе углов размером в половину круга и более. Приближенная оценка этого разрешения не зависит от ширины полосы перестройки частоты и равна
,
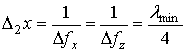где .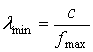

 

Точная оценка разрешения зависит от ширины полосы частот.

При зондировании по полукругу на фиксированной частоте  имеем
 ,

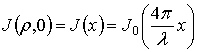где  - функция Бесселя порядка 0, и =0,2 на уровне -4 дБ (или 0,18 на уровне -3дБ, как получено в [6]).

Для секторов  при  получаем сечение функции неопределенности по «азимуту» в виде

                                  (4)

и следующую оценку разрешения РЛИ по «азимуту»: при перестройке частоты от 0 до 200% разрешение  изменяется от 0,2 до 0,37 (или от 0,2 до 0,18, где 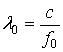, ), как показано на рис.3, где кривая 1 - 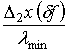, кривая 2 - .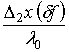

 

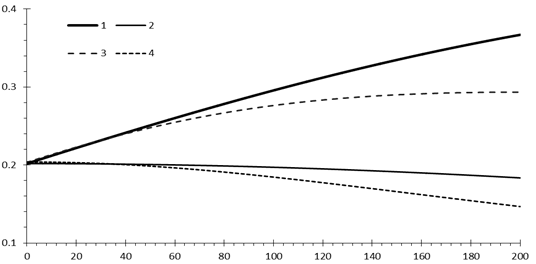
Рис. 3. Разрешение круговых РЛИ в зависимости от  (%)

(1 и 2 -  и , рассчитанные по ; 3 и 4 - по )

Заметим, что разрешение по дальности при интегрировании по полукругу примерно в два раза хуже указанного выше потенциального разрешения поперек [6] и приближается к нему при увеличении размера сектора синтезирования до полного круга. При синтезировании в полном круге получаем так называемые [9] круговые РЛИ, разрешение которых в любом направлении одинаково.

Для получения функции неопределенности инверсно синтезируемых РЛИ в общем случае (для любых значени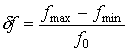й ,  и ) предлагается использовать процедуру преобразования функции неопределенности к виду

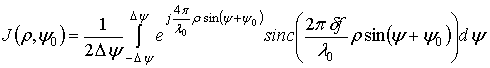
и вычислять ее значения путем однократного суммирования

,

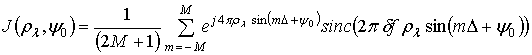где     .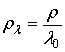

 

При этом в направлениях осей объем вычислений в два раза меньше:

,

, ,

,

, .

 

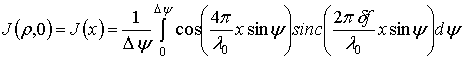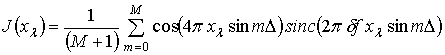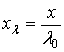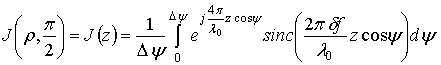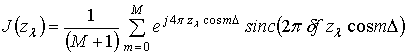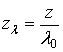Переходя к функции неопределенности  синтезируемых РЛИ по сигналу, преобразованному в область «пространственных частот», отметим, что она описывается выражениями (2) и (3), если в них положить , и оперативно рассчитывается с помощью двумерного обратного быстрого преобразования Фурье. При синтезировании круговых РЛИ объектов эта функция приобретает асимптотически строгое выражение вида [9]

      (5)

где    , ,

 - цилиндрическая лямбда-функция первого порядка,

 - функция Бесселя первого порядка.

Сравнение выражений (4) и (5) показывает, что при  функции  и  совпадают, а при  с увеличением полосы перестройки частоты основной лепесток функции  становится уже, а максимумы боковых лепестков - ниже, чем у функции . Соответственно улучшается и разрешение РЛИ: при перестройке частоты от 0 до 200% рассчитанное по  разрешение  изменяется от 0,2 до 0,29 (или от 0,2 до 0,15), как это показано на рис.3, где кривая 3 - 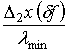, кривая 4 - .

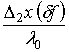Максимальные отличия функций неопределенности  и  имеют место при локации в полосе перестройки частоты, близкой к 200%, что иллюстрируют рис.4 – рис.7, на которых приведены зависимости  - кривые 1 и  - кривые 2 для условий кругового синтезирования () и =30%, 100%, 180% и 200%. Приведенные результаты показывают, что при перестройке частоты до 100% отличия значений функций неопределенности  и  незначительны. Практически значимыми эти отличия становятся для сверхширокополосной локации, - особенно, при приближении к 200% перестройке.

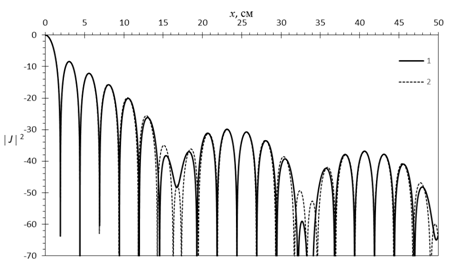
Рис.4.  (кривая 1) и  (кривая 2) при  и =30%

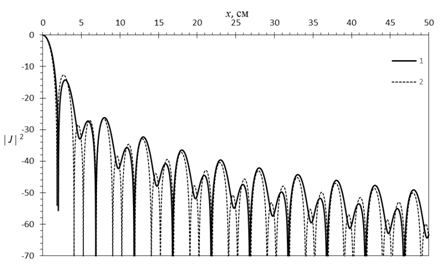
Рис.5.  (кривая 1) и  (кривая 2) при  и =100%

 

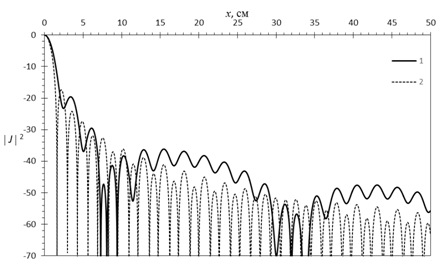
Рис.6.  (кривая 1) и  (кривая 2) при  и =180%

 

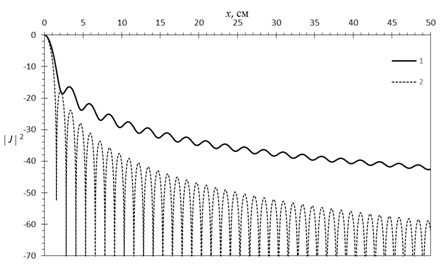
Рис.7.  (кривая 1) и  (кривая 2) при  и =200%

 

Подобным образом расширение полосы перестройки частоты влияет на вид функции неопределенности  в направлениях, отличных от направления «азимута», и для других секторов углов локации, что иллюстрируют рис.8-рис.11, на которых приведены зависимости в относительных единицах (в дБ) квадрата модуля функции неопределенности от расстояния, нормированного к , при =0; 0,1; 0,3; 1; 2: рис.8 –  для ; рис.9 –  для ; рис.10 –  для ; рис.11 –  для . Видно, что в малых секторах углов синтезирования при небольшой полосе перестройки частоты уровень первого бокового лепестка  в направлении дальности и «азимута» равен -13дБ. С увеличением полосы перестройки минимумы в направлении «азимута» «заплывают», а лепестковая структура «сглаживается». В то же время в направлении дальности лепестковая структура отклика сохраняется. При  и небольшой полосе перестройки частоты уровень первого бокового лепестка в обоих направлениях увеличивается до -8дБ. С увеличением полосы перестройки уровень боковых лепестков уменьшается, а лепестковая структура функции «сглаживается».

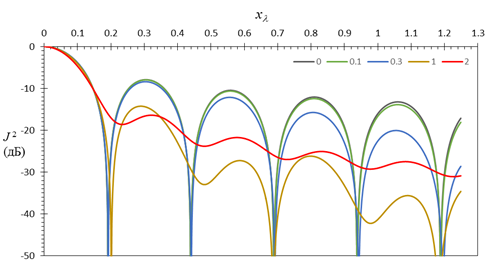
Рис.8.  в дБ при  и =0; 0,1; 0,3; 1; 2

 

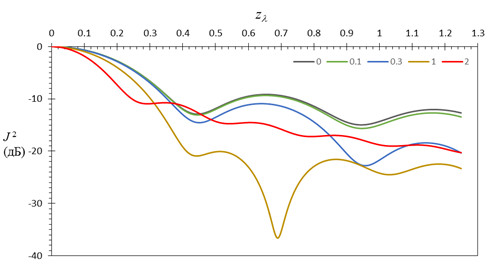
Рис.9.  в дБ при  и =0; 0,1; 0,3; 1; 2

 

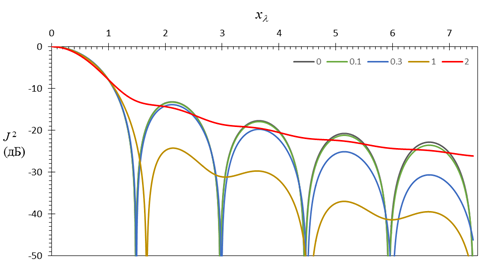
Рис.10.  в дБ при  и =0; 0,1; 0,3; 1; 2

 

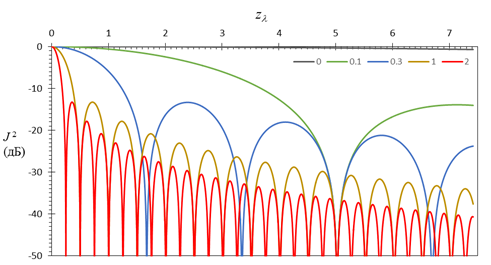
Рис.11.  в дБ при  и =0; 0,1; 0,3; 1; 2

 

Влияние кривизны области определения сигнала на уровень боковых лепестков откликов и их распространение во всех направлениях существенно сказывается при значительном увеличении сектора углов синтезирования РЛИ (±60° и более). В этих условиях оказывается малоэффективной обработка исходного сигнала в одномерных весовых окнах, применяемая для снижения уровня цифрового фона откликов за счет расширения основного лепестка отклика. Весовые окна продолжают эффективно работать в ортогональных направлениях дальность – «азимут», но все хуже с увеличением размера сектора углов интегрирования давят цифровой фон в других направлениях, практически не влияя на уровень цифрового фона круговых РЛИ.

В этой связи возникает вопрос развития теории весовой обработки при инверсном синтезировании РЛИ объектов в больших секторах углов локации. Известны отдельные работы в этом направлении с привлечением метода обратных проекций [10], частично отвечающие на этот вопрос.

В некоторых случаях можно также уйти от этого вопроса ценой незначительного ухудшения разрешающей способности изображения, ограничивая область определения сигнала прямоугольником, интегрируя по которому получаем [8] функцию неопределенности сигнала вида , с уровнем максимума первого бокового лепестка по мощности -13дБ, который (как и уровни прочих «боковиков») эффективно снижается путем обработки сигнала одномерными весовыми окнами.

Так, при синтезировании в полном круге и с учетом обеспечения максимальной перестройки частоты, размер вписанного квадрата будет всего в  раз меньше диаметра круга, а разрешение в такое же количество раз хуже. При синтезировании изображения в секторах углов небольшого размера (рис.2) функции неопределенности по области кругового сектора и по вписанному в нее прямоугольнику с размерами  и , где  и , практически совпадают.

Отметим, что в случае синтезирования сигнала по вписанному в область определения прямоугольнику в секторе углов ±9,7° при =0,3 разрешения по дальности и «азимуту» одинаковы и равны
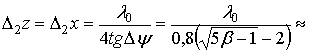1,72, где

,
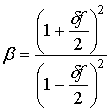что всего на 3% хуже разрешения по Релею 1,67.

Потенциальные разрешения по дальности и «азимуту» в этом случае равны, соответственно, 1,67 и 1,48 (см. рис.12 и рис.13 с рассчитанными для практически важного случая зондирования с перестройкой частоты 30% зависимостями от размера сектора углов синтезирования (в градусах) точных относительных значений (утолщенные линии) разрешений по «азимуту»  и дальности , а также их приближенных значений, оцененных по размеру области «пространственных частот» ). Приближенная оценка разрешений РЛИ по размеру области определения «пространственных частот» в этих условиях - 1,6 и 1,7.

 

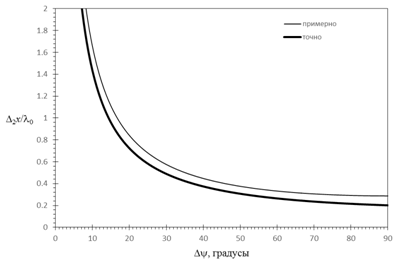
Рис. 12. Разрешение двумерного РЛИ по «азимуту» от  при =0,3

 

 

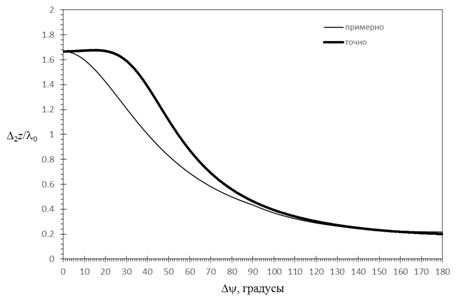
Рис. 13. Разрешение двумерного РЛИ по дальности от  при =0,3

 

Определенный интерес представляет исследование вопроса обеспечения высокого разрешения РЛИ по дальности на фиксированной частоте зондирования за счет увеличения размера сектора углов синтезирования.

Приемлемое разрешение по дальности в этом случае обеспечивается при синтезировании сигнала в секторе углов ±30° и более.

Форма функции неопределенности во всех направлениях при зондировании на фиксированной частоте при увеличении размера сектора углов синтезирования показана на рис.14, где приведены зависимости  в дБ для секторов углов синтезирования ±90° и ±180°.

Интересна оценка влияния на инверсно синтезируемые круговые РЛИ объекта разных методов интегрирования отраженного сигнала, полученного с контролируемой погрешностью. В настоящей работе такая оценка проведена с помощью асимптотически строгих расчетов методом собственных функций сигнала, отраженного металлической сферой диаметром 40 см в полосе перестройки частоты от 0 до 200%: относительно средней частоты 3 ГГц (длина волны 10 см). Рассчитанные РЛИ сферы приведены на рис.15 – рис.20.

 

 

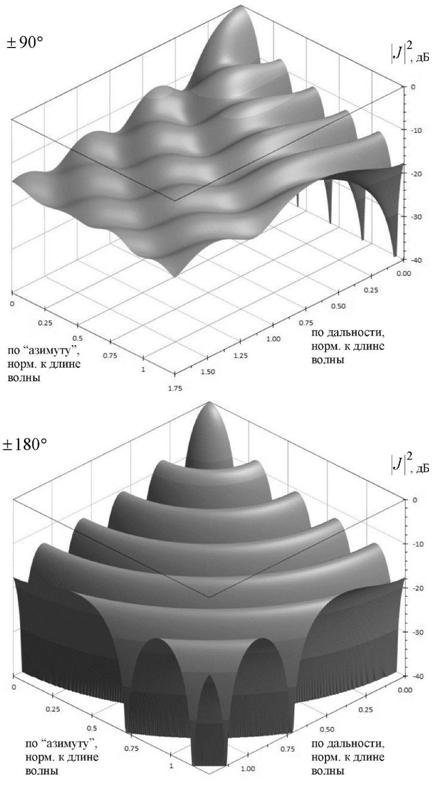
Рис.14. Квадрат модуля функции неопределенности на фиксированной частоте при синтезировании в секторах ±90° и ±180°

 

 

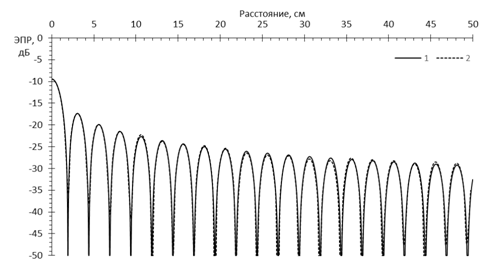
Рис.15. Сечение РЛИ сферы диаметром 40 см в секторе углов синтезирования ±180° на фиксированной частоте 3 ГГц

 

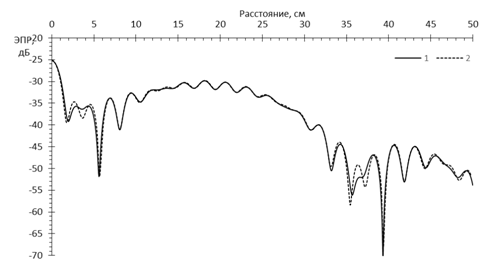
Рис.16. Сечение РЛИ сферы диаметром 40 см в секторе углов синтезирования ±180° и полосе перестройки частоты 30% от 3 ГГц

 

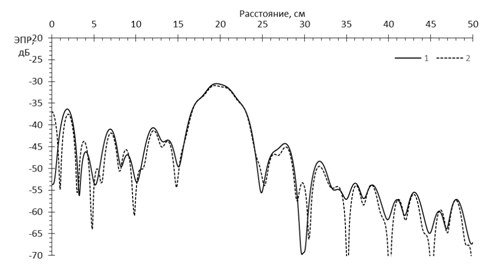
Рис.17. Сечение РЛИ сферы диаметром 40 см в секторе углов синтезирования ±180° и полосе перестройки частоты 100% от 3 ГГц

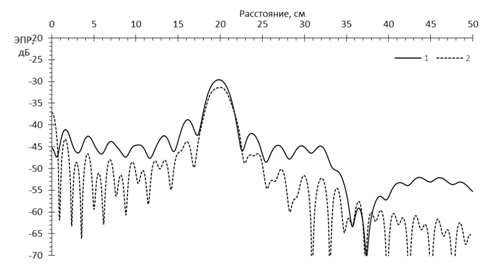
Рис.18. Сечение РЛИ сферы диаметром 40 см в секторе углов синтезирования ±180° и полосе перестройки частоты 180% от 3 ГГц

 

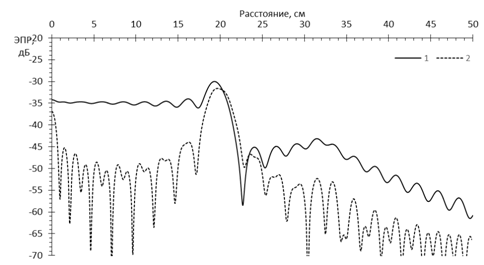
Рис.19. Сечение РЛИ сферы диаметром 40 см в секторе углов синтезирования ±180° и полосе перестройки частоты 200% от 3 ГГц

 

Сплошные кривые 1 на рис.15 – рис. 19 иллюстрируют форму отклика от сферы в единицах ЭПР в любом направлении для сигнала с функцией неопределенности , пунктирные кривые 2 - . По оси значений отложены относительные единицы (дБ), по оси абсцисс – расстояние в см.

Из рис.15 следует, что при зондировании на фиксированной частоте отклик от сферы локализуется в точке, совпадающей с ее центром, а максимум отклика равен ЭПР сферы. Форма отклика от метода интегрирования не зависит.

При ненулевой перестройке частоты (рис.16 – рис. 19) на изображениях в области пространства, занятого сферой, формируется ряд дифракционных максимумов, причем с увеличением полосы перестройки формируется стабильный по уровню мощности отклик от передней кромки сферы, а внутренние максимумы претерпевают динамические изменения уровня мощности с тенденцией к снижению.

При сверхширокополосной локации (в полосе перестройки частоты больше 100% от несущей – рис.18, рис.19) форма откликов зависит от метода синтезирования. При интегрировании по «пространственным частотам», помимо отклика от передней кромки, присутствует постоянный отклик в центре сферы, уровень которого на 4 дБ ниже, а уровни промежуточных откликов резко снижаются, особенно при приближении к 200% перестройке частоты. Прямое интегрирование по частоте и углу дает плавающие по уровню дифракционные максимумы в пространстве внутри сферы, выстраивающие «плато» на уровне -4дБ от максимума отклика передней кромки при приближении к 200% перестройке частоты. Необходимо также отметить, что, в отличие от результатов прямого интегрирования, максимум отклика от передней кромки сферы при интегрировании по «пространственным частотам» на 1,5…2 дБ меньше, а его месторасположение почти строго соответствует координате кромки сферы и практически не испытывает колебаний относительно этой точки при изменении полосы перестройки частоты.

Отмеченные отличия в уровне и местоположении основных откликов от сферы при использовании метода «пространственных частот» незначительны и проявляются в трудно реализуемых на практике условиях сверхширокополосной локации, поэтому не могут служить достаточным основанием для отказа от синтезирования изображений этим методом, имеющим к тому же преимущества в вычислительном отношении и в получаемом разрешении изображений.

Наглядно инверсно формируемые круговые РЛИ сферы, полученные методом «пространственных частот» при 30% и 100% перестройке частоты, в виде цветовой интерпретации ЭПР элементов разрешения на плоскости локации приведены на рис. 20.

 

  

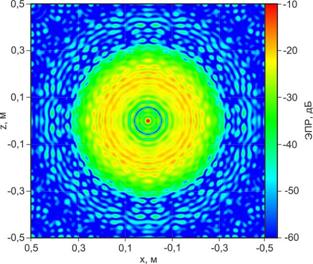
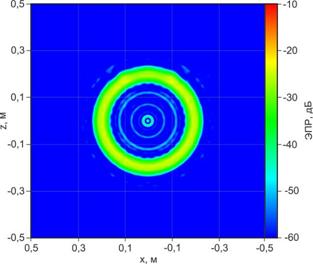
(а)                                                                      (б)

Рис.20. Инверсно синтезированные методом «пространственных частот» круговые РЛИ сферы диаметром 40 см при 30% (а) и 100% (б) перестройке частоты

 

Выводы.

1. В общем случае инверсного синтезирования двумерных РЛИ прибегают к интегрированию по имеющейся круговой области определения отраженного сигнала методом «пространственных частот», что позволяет оперативно получать изображения с потенциально возможным минимальным разрешением. При этом для практики приемлема приближенная оценка разрешения изображений по размеру области «пространственных частот».

Потенциально лучшее и одинаковое во всех направлениях разрешение обеспечивается при синтезировании круговых двумерных РЛИ.

2. Влияние кривизны области определения сигнала на уровень боковых лепестков откликов и их распространение во всех направлениях существенно сказывается при значительном увеличении сектора углов синтезирования РЛИ (±60° и более). В этих условиях обработка сигнала в одномерных весовых окнах, применяемая для резкого снижения уровня цифрового фона за счет расширения основного лепестка отклика, малоэффективна.

3. В частных случаях малых секторов углов или при круговом синтезировании с близкой к 200% перестройкой частоты, ограничение области определения сигнала вписанным прямоугольником позволяет получить изображения с минимальными уровнями цифрового фона при незначительном, с практической точки зрения, ухудшении разрешения.

4. Двумерное РЛИ объекта с приемлемым для практики разрешением по дальности может быть получено и при зондировании на фиксированной частоте, если обеспечиваются условия наблюдения в секторе углов ±30° и более. Такие изображения, однако, не выявляют внутренние особенности и внешний облик отражающих элементов конструкции объекта.

5. Конкретные значения потенциального разрешения и уровней цифрового фона изображений для любых значений полосы перестройки частоты и размера сектора углов синтезирования могут быть получены путем анализа функций неопределенности, рассчитываемых по предложенным процедурам одномерного численного интегрирования.

 

Литература

1. Donald R. Wehner. High-Resolution Radar / Donald R. Wehner. - 2^nd ed. – Boston, London: Artech House, 1995.

2. Chen Victor C. Time-frequency transforms for radar imaging and signal analysis / Victor C. Chen, Hao Ling. – Boston, London: Artech House, 2002.

3.  Ozdemir Caner. Inverse synthetic aperture radar imaging with MATLAB. – Hoboken, NJ, John Wiley & Sons, 2012.

4. A Sourcebook for the Use of the FGAN Tracking and Imaging Radar for Satellite Imaging. // [Электронный ресурс]. URL: http://fas.org/spp/military/program/track/fgan.pdf

5. Методы исследования радиолокационных характеристик объектов. Монография / Под ред. С.В. Ягольникова. – М.: «Радиотехника», 2012.

6. Кондратенков Г.С., Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли. Учебное пособие для вузов / Под ред. Г.С. Кондратенкова. – М.: «Радиотехника», 2005. - 368с.

7. Моряков С.И., Нестеров С.М., Скородумов И.А. Алгоритм формирования двумерных радиолокационных изображений объекта на основе синтезирования апертуры и согласованной обработки по пространственным частотам // Труды XXVIII Всероссийского симпозиума «Радиолокационное исследование природных сред». -  СПб: ВКА им. А.Ф. Можайского, 2013.

8. С.И. Моряков, С.М. Нестеров, И.А. Скородумов. Функция неопределенности радиолокационного сигнала при синтезировании двумерного радиолокационного изображения летательного аппарата // «Радиотехника и электроника», 2012, том 57, № 8.

9. Wei Yan, Nai-Zhi Wang, Amna Ajaz, and Jia-Dong Xu. A Novel Imaging Method for Inverse Scattering Problem Using Stepped-frequency Waveforms // Progress In Electromagnetics Research Symposium Proceedings, Suzhou, China, Sept. 12-16, 2011.

10. Allen J. Bric. Imaging a BQM-74E Target Drone Using Coherent Radar Cross Section Measurements // Johns Hopkins APL technical digest, vol.18, November 3, 1997.