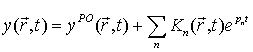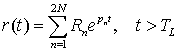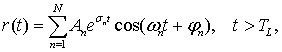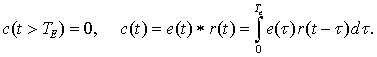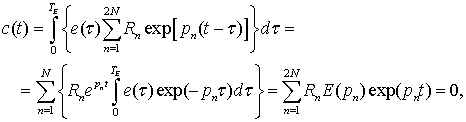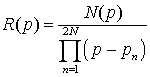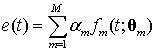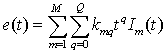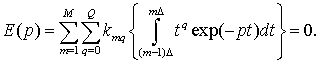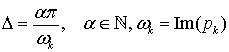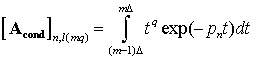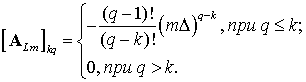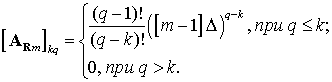УДК: 621.396.96

СИНТЕЗ И ОПТИМИЗАЦИЯ ПОСЕКЦИОННОГО ПОЛИНОМИАЛЬНОГО Е-ИМПУЛЬСА ПРИ РЕШЕНИИ ЗАДАЧИ РАЗЛИЧЕНИЯ ОБЪЕКТОВ ПО СОБСТВЕННЫМ РЕЗОНАНСАМ

 

Д. В. Филимонова, Т. Я. Шевгунов

Московский авиационный институт (национальный исследовательский университет)

 

Статья получена 22 марта 2015 г.

 

Аннотация. В статье рассмотрены теоретические основы метода Е‑импульса (гасящего импульса), позволяющего построить систему распознавания объектов на основе обработки поздневременной части их отклика на широкополосное электромагнитное воздействие. Показано, что проведение процедуры синтеза максимально гладкого Е‑импульса, состоящего из последовательных секций, базисными функциями которых являются полиномы, накладывает строгое соотношение между числом секций, числом идентифицируемых резонансов и порядком полинома. В рамках структурной схемы системы распознавания объектов на основе метода Е-импульса исследована зависимость дискриминационного числа Е‑импульса, скалярного критерия, от длительности его секции и используемого порядка базисного полинома. Результаты статистического моделирования различения откликов от двух масштабных моделей самолётов показали, что использование Е‑импульса с оптимальными параметрами способно обеспечить различение объектов при малых отношениях сигнал-шум.

Ключевые слова: Е-импульс, гасящий импульс, метод сингулярного разложения, собственные резонансы, распознавание радиолокационных целей, цифровая обработка сигналов.

Abstract: In this paper, the foundation of E-pulse (extinction pulse) method is considered as a possible way to design a target discrimination scheme using reflected responses for wideband electromagnetic incident pulse. The synthesis procedure of subsectional maximally smooth polynomial E-pulse appears to assume the equation taken for the number of sections, the number of natural resonances and the used polynomial order. In accordance with discrimination system structure, the E-pulse discrimination number dependency on section width and polynomial order is investigated. The results of statistical simulation for the two target problem show that E-pulse built for optimal parameters preserves enough discriminating potential for low signal-to-noise ratio.

Key words: E-pulse, extinction pulse, SEM, natural resonances, radar target discrimination, digital signal processing.

1. Введение

На протяжении последних десятилетий остаётся актуальной задача различения технических объектов на основе обработки электромагнитного поля, рассеянного ими при облучении радиосигналами с широкими спектрами. Решение электродинамической задачи отыскания математической формы отклика цели конечных размеров на возбуждающее широкополосное электромагнитное колебание, представляющее собой плоскую электромагнитную волну, было найдено К. Баумом и представлено в ставшей классической работе [1] как метод сингулярного разложения.

Согласно методу сингулярного разложения, отраженный от объекта радиолокационный сигнал, порождаемый наводимым в цели электромагнитным полем вследствие ее облучения, во временной области может быть разделен на два интервала: ранневременной, когда возбуждающая электромагнитная волна отражается от “блестящих точек” цели, и поздневременной, наступающий после прохождения волной всей цели. В течение поздневременного интервала времени наблюдаются свободные колебания поля, порожденные токами, индуцированными на поверхности проводящего объекта.

В работе М. Моргана [2] приводится детальное объяснение процесса формирования отраженной волны телом геометрически сложной формы с проводящей поверхностью. Так сформированный отклик объекта может быть представлен моделью:

                                        ,                                (1)

где  – часть отклика, описываемая моделями физической оптики,  – коэффициенты, зависящие от ракурса и времени, p_n – полюса, характеризующие собственные моды объекта. Согласно методу сингулярного разложения значения полюсов определяются структурой облучаемой цели и остаются постоянными при изменении ракурса цели относительно источника её облучения.

Поздневременной интервал t > T_L начинается после наступления двух событий. Первое состоит в том, что завершается конечный во времени отклик , а второе – в том, что коэффициенты  становятся постоянными во времени . Тогда модель поздневременной части принятого отклика имеет следующую запись в комплексной (2) и действительной (3) форме:

                                                ,                                        (2)

                                   ,                                (3)

 

где p_n = σ_n + jω_n – собственные частоты, или полюса на комплексной плоскости, характеризующие доминирующие собственные моды. Полюса p_n, формирующие действительный отклик, образуют N комплексно-сопряженных пар. A_n и φ_n – соответственно амплитуда и начальная фаза затухающей гармоники, зависящие от ракурса цели и составляющие вычеты в комплексной форме: R_n = A_n∙exp(jφ_n). T_L –момент начала поздневременного интервала.

Таким образом, каждая цель может быть описана уникальным инвариантным к ракурсу признаком – набором полюсов, соответствующих комплексным резонансам облученного объекта. Один из способов построения системы различения целей состоит в извлечении набора полюсов из поздневременной части отклика с использованием таких методов как параметрический метод Прони [3], генетические алгоритмы [4] или метод матричных пучков [5]. Главным недостатком указанных методов является их высокая вычислительная сложность: так, в основе метода Прони лежит решение нелинейного уравнения высокого порядка, метод матричных пучков построен на основе сингулярного разложения матриц, а генетические алгоритмы представляют собой итеративные процедуры, имитирующие процессы естественного отбора.

Альтернативным подходом к решению задачи различения является рассматриваемый в настоящей работе метод Е‑импульса. Данный метод состоит в построении по набору полюсов цели сигнала конечной длительности, который может быть использован как широкополосный облучающий импульс. Результатом взаимодействия такого импульса с объектом, для полюсов которого он построен, будет отклик, в поздневременном интервале которого не будет наблюдаться свободных колебаний. В связи с техническими сложностями при построении приемо-передающих трактов, сохраняющих форму широкополосного сигнала, более продуктивная схема предполагает использование Е‑импульса в качестве импульсной характеристики фильтра, на вход которой подаётся отклик цели на сверхширокополосное воздействие сравнительно простой формы. В этом случае анализу подвергается сигнал на выходе фильтра.

Во второй части настоящей статьи представлены теоретические основы метода Е‑импульса и сформулированы необходимые условия его существования во временной области и в области комплексной частоты. Также рассмотрена процедура синтеза гладких посекционных полиномиальных Е‑импульсов с учётом граничных условий и представлены примеры сигналов для многорезонансных объектов. В третьей части статьи описан интегральный критерий оценки отклика в пределах поздневременного интервала и рассмотрена схема различения откликов объектов, построенная на основе фильтров с конечными импульсными характеристиками, в качестве которых используются Е‑импульсы, синтезированные по наборам полюсов из библиотеки целей. В четвертой части представлены результаты исследования по оптимизации параметров Е‑импульса, направленной на повышение его дискриминационной характеристики. В заключении приведены выводы и рассмотрены перспективы дальнейшего развития метода.

 

              

           а)                                                           б)

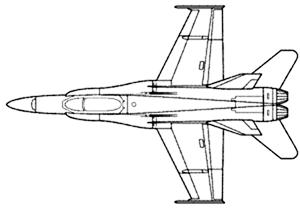
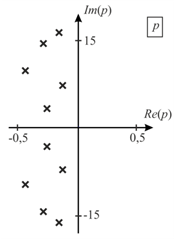
Рис. 1. Модель самолёта McDonnel Douglas F-18 (а) и соответствующая ей диаграмма полюсов на комплексной плоскости (б).

 

              

       а)                                                           б)

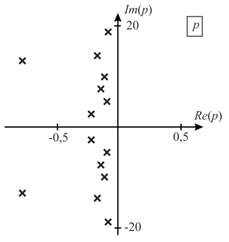
Рис. 2. Модель самолёта Boeing 707 (B-707) (а) и соответствующая ей диаграмма полюсов на комплексной плоскости (б)

При проведении имитационного моделирования с использованием алгоритмов, основанных на методе Е‑импульса, в настоящей работе используются масштабные модели двух самолетов: Boeing 707 (B-707) и McDonnel Douglas F-18 размерами 33 и 38,5 см, значения собственных резонансов которых были получены на основе экспериментальных измерений и впервые опубликованы в статье [6]. Эскизы моделей самолетов F-18 и B-707, а также соответствующие им диаграммы полюсов представлены соответственно на рис. 1 и рис. 2.

2. Теоретические основы метода Е-импульса

Е-импульс (от англ. extinction-pulse, “гасящий импульс”) – это сигнал e(t) конечной длительности T_E, подбираемый к сигналу r(t), имеющему начало, так, что свёртка с(t) сигналов e(t) и r(t) равна нулю, начиная с момента времени t ≥ T_E.

Формально, без потери общности, можно положить, что сигналы e(t) и r(t) начинаются не раньше нуля. Тогда Е-импульс может быть представлен в виде аналитической записи, включающей в себя два условия:

                                                                                              (4)

                                                 (5)

 

Первое условие является условием конечной длительности Е-импульса, а второе – необходимым условием во временной области. Подстановка отклика r(t) в комплексной форме (2) в определяющую формулу (5) позволяет сформулировать условие в частотной области. Так при t >T_E выражение для c(t) имеет вид:

                               (6)

где

 –

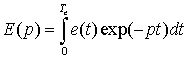изображение (преобразование Лапласа) гасящего импульса e(t).

Из последнего преобразования следует, что в силу линейной независимости слагаемых R_nexp(p_nt) при различных значениях полюсов p_n для выполнения условия (5) должно быть выполнено следующее условие в частотной области:

.                                                                                                  (7)

Таким образом, изображение E(p) должно обращаться в нуль при подстановке в него каждого из полюсов R(p), что является необходимым условием существования Е-импульса, сформулированным в частотной области.

Изображение R(p) для сигнала r(t), заданного согласно (2), принимает вид правильной рациональной дроби:

,                                                                                             (8)

где N(p) –полином степени не выше 2N–1.

Поскольку сигналы e(t) и c(t) представляют собой финитные сигналы, то изображения E(p) и C(p) должны быть целыми функциями комплексной частоты p. Математическое доказательство этого утверждения применительно к решению подобного класса задач приводится в статье [8].

Переход к изображениям сигналов R(p), E(p) и C(p) позволяет составить системное соотношение, эквивалентное (5):

.                                                                                              (9)

Тогда для обеспечения условия конечной длительности c(t) при условии конечной длительности e(t) необходимо, чтобы знаменатель дроби R(p) был сокращен множителями, содержащимися в E(p), т.е. чтобы полюса R(p) совпадали с нулями E(p). Изображение E(p) может иметь дополнительные нули, и будет иметь вид:

,                                                                                  (10)

 

где D(p) – некоторая целая функция.

2.1 Синтез Е-импульса

Среди известных подходов к синтезу сигнала e(t), обладающего свойствами (4) и (5), наиболее простым с точки зрения аналитических преобразований и практической реализации является предложенный авторами оригинального метода параметрический подход [7, 9], при котором Е‑импульс рассматривается как линейная комбинация конечного числа базисных функций f_m(t; θ_m):

,                                                                                          (11)

 

где θ_m представляет собой вектор параметров для m-ой базисной функции f_m(t; θ_m). Тогда для того чтобы синтезировать Е-импульс будет достаточным решить задачу определения всех векторов параметров {θ_m}, удовлетворяющих необходимому условию Е-импульса, сформулированному во временной области (5) или равносильному ему в частотной (7).

Если функции f_m(t; θ_m) не перекрываются во времени, то говорят, что они образуют секции, а сформированный ими Е-импульс называют посекционным и состоящим из M секций. В этом случае гарантируется, что слагаемые f_m(t; θ_m) будут линейно независимыми базисными функциями, для которых выбирается общая структура, заданная некоторым аналитическим выражением. При синтезе сигнала Е-импульса в качестве базисных функций f_m(t; θ_m) могут быть использованы полиномы различного типа (Чебышева, Эрмита, и т.д.), β‑сплайны [10], экспоненциальные импульсы, затухающие гармоники, и др.

Наиболее простым случаем является выбор такого базиса f_m(t; θ_m), элементы которого зависят от параметров вектора θ_m линейно. В этом случае решение задачи можно получить путём составления и решения системы линейных алгебраических уравнений вида

                                                            ,                                                  (12)

где A и b – соответственно матрица системы и вектор правой части, а x – вектор решений, составленный из всех элементов векторов θ_m.

Рассмотрим построение посекционного полиномиального Е-импульса – сигнала, базисными функциями которого являются полиномы, ограниченные в пределах секций одинаковой длительности. Аналитическое выражение такого Е‑импульса является частным случаем общей модели (11) и задается следующим выражением:

,                                                                                        (13)

где Q – выбранный порядок полиномов, M – количество секций, Δ – длительность секции, которая, как правило, выбирается разбиением длительности Е-импульса T_E на равные интервалы: Δ = T_E/M, k_mq – M×(Q+1) неизвестных коэффициентов полиномов Е-импульса. Индикаторная функция I_m(t) обеспечивает существование m-ого полинома строго в пределах m-ой секции:

,                                                                        (14)

где u(t) – функция Хевисайда (единичная ступенчатая функция).

Необходимое условие в частотной области (7) позволяет записать 2N уравнений, по одному для каждого из полюсов p_n и сопряженного ему  вида:

                                                          (15)

Для однозначного вычисления всех коэффициентов k_mq, общее число которых M×(Q+1), необходимо добавить к составленным по формуле (15) еще M×(Q+1) – 2N уравнений. В работе [11] было предложено составить эти уравнения так, что обеспечить непрерывность полиномов и их производных на границах секций. Авторами данной работы предложенный подход был обобщён, что позволило сформулировать условия непрерывности и гладкости сигнала Е-импульса не только между секциями, но и на границах сигнала. Соблюдение указанных условий позволяет синтезировать максимально гладкий сигнал, который обладает двумя отличительными свойствами:

1) сигнал и его производные, вплоть до Q – 1, являются гладкими, что обеспечивает возможность физической генерации и излучения;

2) сигнал имеет компактный спектр в частотной области, сосредоточенный в области низких частот, что позволяет исключить высокочастотный шум за счёт уменьшения рабочей полосы приёмника.

Авторами настоящей статьи получено соотношение, определяющее количество секций M Е-импульса для синтеза сигнала (13), в форме равенства:

,                                                                                              (16)

где S – число, зависящее от количества полюсов объекта, к которому подбирается Е-импульс, и длительности секции, Q – порядок полинома, R – число дополнительных условий.

Добавление единицы в правой части (16) необходимо для подсчета уравнения, порожденного свойством линейности: если некоторый сигнал e(t) является Е-импульсом, то и сигнал Ke(t), где , тоже будет Е-импульсом.

В общем случае число S равно полному количеству полюсов объекта S = 2N, что соответствует числу уравнений, составленных согласно (15). Однако если длительность секции Δ будет такой, что для k-го полюса выполняется соотношение

                                                                             (17)

 

то это приведет к образованию двух линейно-зависимых (в частном случае, одинаковых) уравнений типа (15). Следствием этого является уменьшение числа S в соотношении (16) на единицу: S = 2N – 1, что влечет уменьшение количества секций Е-импульса M на одну. Такой Е-импульс получил название собственного (natural) и подробно рассмотрен в статье [9]. Если данное замечание не учесть, то матрица A в (12) окажется с дефицитом ранга, а система (12), оставаясь совместной, будет иметь бесконечное число решений. В случае, когда длительность секции Е-импульса не удовлетворяет условию (17) ни для одного из полюсов, матрица A имеет полный ранг, система уравнений сохраняет (12) единственное решение, а Е-импульс именуется вынужденным (forced).

С учетом выше представленных условий матрицу A можно сформировать в виде блочной матрицы, структура которой представлена на рис. 3. В уравнениях слагаемые, содержащие коэффициенты, записываются слева направо по возрастанию номера секции m, а затем по возрастанию степени q слагаемых, составляющих полином в пределах каждой секции: от нулевой до Q.

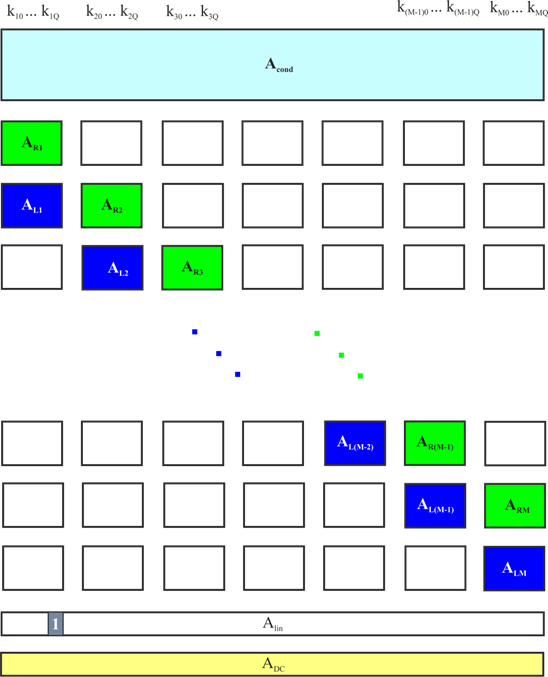
Рис. 3. Матрица A в блочном представлении.
Белыми прямоугольниками обозначены полностью нулевые подматрицы.

Таким образом, система уравнений (12) решается относительно коэффициентов полиномов Е‑импульса k_mq, размещенных в столбце x в следующем порядке: элемент k_mq занимает позицию x_l, номер которой l вычисляется по формуле:

 l =l(m,q)= (m – 1)(Q + 1) +q+ 1.                                                                         (18)

Элементы матрицы A_cond размером S×M(Q+1) представляют собой коэффициенты при неизвестных k_mq, полученные путём интегрирования при соответствующих значениях номера секции m, порядка полинома q и номера полюса в соответствии с уравнениями (15):

.                                                                       (19)

 

Матрицы A_Rm, A_Lm содержат коэффициенты при степенях переменной t полученные из уравнений, задающих непрерывность и гладкость на границах сигнала и между секциями. Элементы этих матриц вычисляются по формулам:

                                                             (20)

                                                        (21)

Условие линейности позволяет задать значение одного из коэффициентов произвольно. Положим, что коэффициент при старшей степени t^Q первой секции k_1Q равен единице, добавив для этого соответствующую строку в матрицу A.

Также матрица может быть дополнена R строками, отражающими дополнительные условия. Примером такого условия служит условия Е‑импульса нулевой площади, или DC E-pulse [7].

Длина вектор-столбца b, стоящего в правой части (12), равна числу неизвестных. Все элементы вектора b нулевые за исключением единицы, стоящей в позиции с номером S+(M+1)×(Q+1)+1, соответствующим номеру строки, записанной с использованием свойства линейности.

2.2 Пример синтеза

Для демонстрации работы алгоритма синтеза Е-импульса и проявления характерных свойств метода во временной области, описанных выражениями (4) и (5), в настоящем разделе приведен пример синтеза Е‑импульсов различного порядка для модели самолёта F-18.

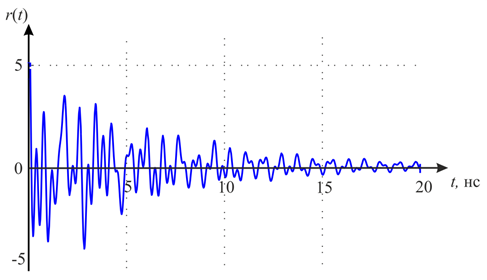
По известному набору полюсов самолета (рис. 1) был аналитически восстановлен отклик объекта r(t) продолжительностью порядка 20 нс, соответствующий модели поздневременной части (2). Во временной области отклик цели F-18 имеет вид, представленный на рис. 4.

 

Рис. 4. Временной отклик модели F-18

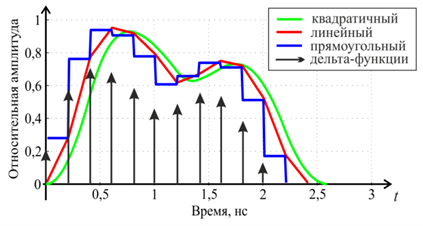
Для выбранной радиолокационной цели были синтезированы посекционные Е‑импульсы типа “forced” с нормированной энергией, составленные из полиномов разного порядка Q: нулевого (прямоугольный Е‑импульс), первого (линейный) и второго (квадратичный). Длительность секции Δ была выбрана равной 0,2 нс. На рис. 4 приведен результат синтеза Е‑импульсов, с учётом нормировки их энергии. Также для сравнения на том же рисунке представлен Е-импульс, составленный из дельта-функций (формально его порядок Q = –1).

Анализ графиков на рис. 5 позволяет отметить, в первую очередь, что при увеличении порядка полиномов (Q = –1; 0; 1; 2) увеличивается количество секций, составляющих Е-импульс соответствующего порядка. Это изменение полностью согласуется с формулой (16). Кроме этого, форма Е‑импульсов позволяет убедиться, что выполняются предложенные условия непрерывности для полиномов порядка Q ≥ 1 и гладкости для Q ≥ 2. Для всех порядков также выполняется требование конечной длительности Е-импульса (4).

 

Рис. 5. Е-импульсы типа “forced” различного порядка для модели F-18

 

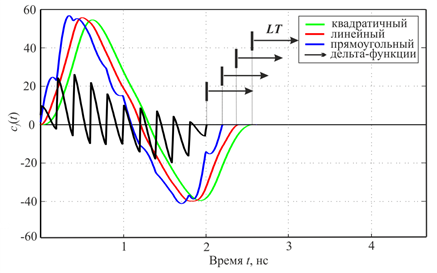
Рис. 6. Результат свертки отклика с Е-импульсами

Отображенные на рис. 6 графики результатов свёртки дают наглядное представление о проявлении основного действия Е-импульса во временной области (5). Свертка отклика с Е-импульсом, так же как и сам Е-импульс, является конечной, и длительность свёртки равна длительности Е-импульса, несмотря на то, что эффективная длительность отклика составляет 20 нс, в то время как длительности Е-импульсов составляют величины 2–2,5 нс.

3. Применение Е-импульса для идентификации объектов

Свойство Е-импульса обнулять (5) при свертке сигнал, соответствующий резонансной модели (2), позволяет синтезировать структуру системы для различения целей, использующую для принятия решений критерий минимума интегрального признака – дискриминационного числа Е-импульса.

3.1 Дискриминационное число

Детальный анализ свёртки с(t) показывает, что границей её раздела на две характерные части служит момент времени T_LT, равный сумме длительности Е‑импульса T_E и T_L – длительности ранневременной части отклика. Далее в этом разделе, а также при моделировании полагается, что соответствие импульсной характеристики модели (3) начинается c нулевого момента, т.е. T_L = 0, а T_LT = T_E.

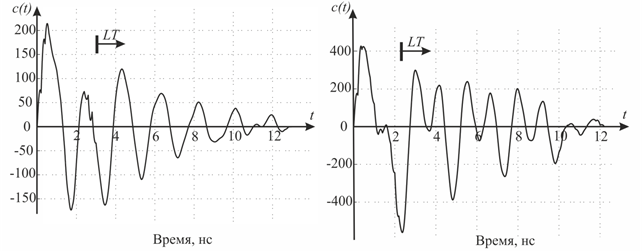
Ключевая идея, лежащая в основе способа распознавания, основанного на методе Е‑импульса, состоит в том, что свертка Е-импульса e_X(t), подобранного к полюсам некоторой цели X, с откликом этой цели r_X(t) стремится к нулю на протяжении поздневременного периода (late-time, LT): с_XX(t > T_LT) ≡ 0. Но свертка этого же Е-импульса с сигналом другой цели Y r_Y(t) в поздневременной период будет существенно ненулевой: с_XY(t > T_LT) ≠ 0. На рис. 7 приведены случаи перекрестных сверток: отклика модели F-18 с E-импульсом, подобранным для B-707, на рис. 7 (а) и отклика модели B-707 с E-импульсом, подобранным для F-18, на рис. 7 (б).

Для количественной оценки качества идентификации в [13] было предложено дискриминационное число Е-импульса (E‑pulse discrimination number), обозначаемое через EDN и вычисляемое для свертки Е-импульса, построенного для цели X с откликом цели Y:

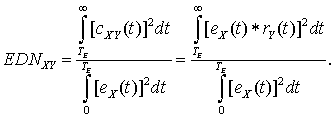                                                        (22)

Параметр EDN может быть вычислен экспериментально; он имеет физический смысл отношения энергии свертки c_XY(t) в поздневременной период (t > T_LT) к энергии Е-импульса e_X(t). Очевидно, что если цели совпадают, т.е. Y = X, дискриминационное число будет равно нулю EDN_XX = 0.

 

а) Отклик от F-18, Е-импульс к B-707  б) Отклик от B-707, Е-импульс к F-18

Рис. 7. Перекрестные свертки откликов и Е-импульсов для двух целей

3.2 Система распознавания на основе фильтра Е-импульса

В первых опубликованных работах [6, 9] по методу Е-импульса предполагалось, что непосредственно синтезированный сигнал e(t) будет излучен в направлении цели, а отклик цели на него будет принят и обработан аналоговыми или цифровыми системами. Однако непосредственное применение такого подхода на практике оказывается неэффективным.

Одной из главных причин этого является то, что спектр Е-импульса широкий и сконцентрирован в области низких частот: для гладких Е‑импульсов (второго порядка и выше) ширина спектра может быть оценена как величина, обратная длительности одной секции. Е‑импульс является сверхширокополосным импульсным сигналом, форма которого определяет его действие. Для минимизации искажения формы сигнала при передаче и приёме необходимо использовать устройства с равномерной передаточной характеристикой в сверхширокой полосе частот, а дальность распространения такого сигнала оказывается ограниченной в силу дисперсионных свойств среды распространения.

Поэтому в работе [12] было предложено рассмотреть системное соотношение (9) так, чтобы в нём роль системной функции фильтра выполняло изображение Е-импульса E(p), а входным сигналом был отклик цели на импульсное воздействие простой формы, обладающее достаточной шириной спектра, чтобы возбудить собственные резонансы, необходимые для достоверного различения целей. В том случае, когда E(p) играет роль системной функции, сигнал e(t) является импульсной характеристикой фильтра, который называют фильтром Е-импульса. Заметим, что в силу определения (4) такой фильтр будет относиться к классу фильтров с конечной импульсной характеристикой (КИХ-фильтров).

В условиях реальных измерений при возбуждении цели достаточно широкополосным воздействием принимаемый от цели отклик z(t) при t > T_L может быть представлен моделью суммы полезного сигнала и шума:

z(t) = S·r(t) + n(t),                                                                                               (23)

где S – площадь широкополосного возбуждающего импульса, r(t) – информационный сигнал, представляющий собой модель (2), n(t) – аддитивный белый гауссовский шум (АБГШ).

Поскольку при формировании свёртки на основе принятого сигнала вместо сигнала r_X(t) будет использоваться зашумленный z_X(t), свертка последнего с Е‑импульсом e_X(t) окажется ненулевой при t > T_LT. Таким образом, появляется задача различения зашумленного сигнала z_X(t) и всех прочих сигналов z_Y(t) (X ≠ Y), сформированных в соответствии с моделью (23).

Распознавание неизвестной цели, т.е. отнесение её к известному классу по результатам обработки её отклика, предполагает последовательное сравнение признаков цели, выделенными из отклика с признаками известных классов целей, называемых эталонами. Метод Е-импульса предполагает использование интегральной меры сравнения, которой служит скалярная оценка EDN принимаемого отклика при использовании Е-импульса, подобранного к набору полюсов каждой из ожидаемых N целей.

На рис. 8 представлена структурная схема системы различения объектов по собственным резонансам, построенная на основе метода Е‑импульса [14].

 

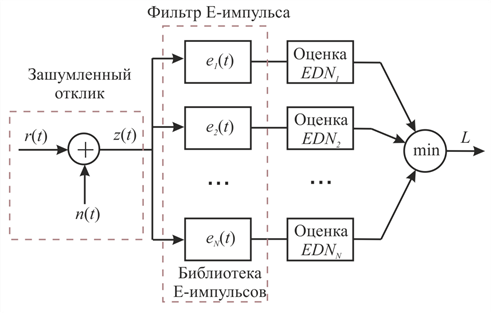
Рис. 8. Структурная схема распознавания объектов

На вход системы распознавания поступает зашумленный отклик z(t) от объекта, который проходит одновременно через N фильтров Е-импульсов e_i(t), i = 1,…,N, соответствующих каждой из целей, содержащейся в библиотеке эталонов. Для каждого из выходных сигналов с_i(t) фильтров производится оценка параметров EDN_i, (i = 1,…,N) путём измерения энергии поздневременной части (t > T_LT). Среди вычисленных {EDN_i,} выбирается наименьшая из оценок EDN_min = min{EDN_i}, соответствующая эталону цели с некоторым номером L: EDN_min = EDN_L, и наблюдаемая цель классифицируется как цель с номером L из библиотеки целей.

Дискриминационное число EDN является интегральной скалярной мерой свертки Е‑импульса с приходящим от неизвестной цели откликом. В случае если цель окажется именно той, по набору полюсов которой построен фильтр Е‑импульса, значение EDN будет стремиться к нулю при возрастании отношения сигнал/шум. В противном случае, когда на вход фильтра подаётся отклик другой цели, значение EDN будет существенно отлично от нуля, как при малом уровне шума, так и при значительном.

Для оценки качества метода различения целей с использованием Е‑импульса было проведено статистическое моделирование в присутствии АБГШ различного уровня. Было рассмотрено 2 сценария моделирования: в первом из них Е-импульс подбирался к цели B-707, а во втором – к F-18. Принимаемыми откликами являются отклики обеих целей. Таким образом, в каждом из случаев Е-импульс сворачивался с ожидаемым и альтернативным откликом. Ниже представлены зависимости дискриминационного числа от величины отношения сигнал-шум (в дБ) для соответствующих случаев подбора Е-импульса.

 

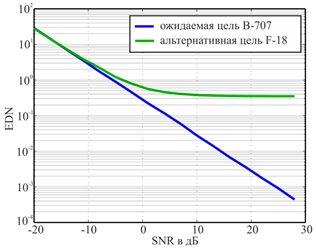
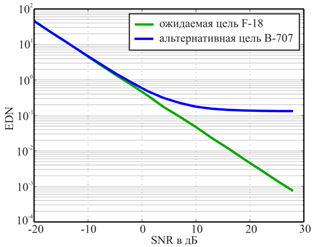
         а) B-707 - ожидаемая цель                     б) F-18 - ожидаемая цель

Рис. 9. Зависимость качества идентификации от отношения сигнал-шум

При данном способе построения графика в логарифмическом масштабе зависимость EDN от отношения сигнал-шум для ожидаемого отклика представляет прямую линию. Это объясняется тем, что в поздневременной части свертки c(t>T_E) Е‑импульса с зашумленным откликом подобранной к нему цели будет присутствовать только шум. Разность между EDN для своей и альтернативной цели непосредственно влияет на качество алгоритма различения целей: чем эта разность больше, тем выше будет вероятность правильного различения целей. Таким образом, достоверную идентификацию представляется возможным произвести для отношений сигнал-шум, выше некоторого уровня. Из графиков видно, что для верного различения цели B-707 минимально допустимое отношение сигнал-шум 0 дБ, а для различения F-18 – 5 дБ.

4. Повышение качества идентификации: оптимизация параметров Е‑импульса

В научных публикациях по тематике Е-импульса большое внимание традиционно уделяется описанию феномена обнуления свертки, процедуре синтеза и структуре системы; при этом авторами не приводятся какие-либо рекомендации по выбору формы и длительности Е‑импульса.

Авторы настоящей работы выявили [15], что эффективность использования метода Е-импульса для различения целей может быть существенно повышена, если значения параметров – длительность секции Δ и порядок полиномов Q – будут выбраны оптимальными. Аналитическое решение этой задачи оптимизации требует привлечения сложного математического аппарата в силу структурной и нелинейной зависимости показателя EDN от указанных параметров, а также необходимости априорных знаний о собственных резонансах модели (2). Поэтому на текущем этапе для решения задачи оптимизации предложено использовать численное моделирование.

Таблица 1. Зависимость качества идентификации от параметров Е-импульса

EDN		Длительность секции Δ, нс
		0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5
Порядок Q	0	0,06	0,33	12871	1231	408	566	1651	503	4065	2974
	1	0,07	0,47	15651	1187	346	484	1008	188	3795	1795
	2	0,08	0,54	14276	1118	295	433	798	90	3211	1308
	3	0,08	0,66	11300	1025	263	397	687	43	2418	1082

 

В результате проведенного моделирования была построена двумерная функция зависимости дискриминационного числа от параметров посекционного полиномиального Е-импульса. Значение EDN вычислялось для сверток отклика цели F-18 и Е-импульсов, подобранных к полюсам цели B-707, составленных из секций длительностью от 0,02 до 0,5 нс и содержащих полиномы от нулевого до пятого порядка. Полученные результаты для значений секций кратных 0,05 нс и порядков от нулевого до третьего представлены в табл. 1.

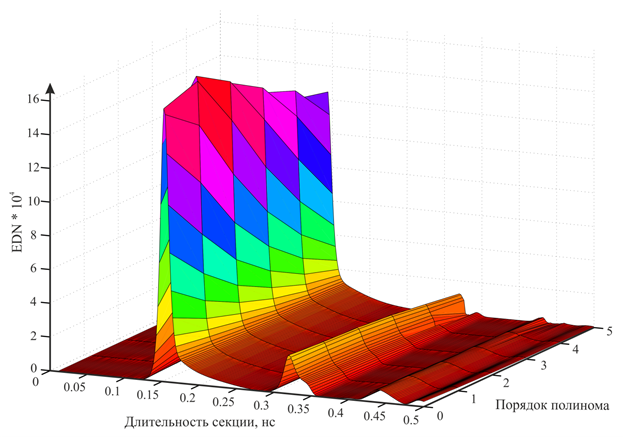
Анализ таблицы 1 показывает, что для различения цели B-707 от цели F-18 можно построить Е‑импульс с оптимальными параметрами в соответствии с максимальной величиной дискриминационного числа. Общий характер зависимости EDN от длительности секции и порядка представлен на рис. 10 посредством трехмерной поверхности. Для данного примера максимум достигается при длительности секции 0,15 нс и секциях, заданных в виде линейных базисных функций. Необходимо отметить, что влияние порядка на величину EDN незначительно, в то время как зависимость от длительности секции имеет сложный характер: наблюдаются локальные максимумы в окрестностях некоторых значений.

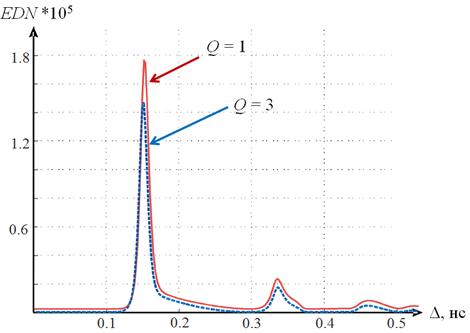
На рис. 11 представлены два сечения трехмерной поверхности (рис. 10), соответствующие первому и третьему порядку полиномов. Сечения, полученные при моделировании с меньшим шагом разбиения диапазона значений длительности секции, позволяют выявить достаточно острый пик в окрестности значения 0,15 нс, характерный как для линейного, так и кубического полиномов.

Для иллюстрации повышения дискриминационных свойств Е-импульса при оптимизации его параметров представим зависимость среднего значения дискриминационного числа Е‑импульса (EDN) от отношения сигнал-шум. На рис. 12 приведены результаты статистического моделирования оценки среднего значения EDN для ожидаемой цели (B-707), к которой подобран Е‑импульс, и другой цели (F-18) при произвольно выбранных и при оптимальных параметрах Е-импульса.

Рис. 10. Зависимость качества идентификации от параметров Е-импульса

 

Рис. 11. Зависимость дискриминационного числа Е-импульса от длительности секции при первом и третьем порядке полиномов.

Анализ графика зависимости EDN от отношения сигнал/шум (SNR) на рис. 12 позволяет утверждать, что достоверное различение ожидаемой цели и альтернативной возможна лишь при тех значениях уровня шума, где разность значений EDN для своей и альтернативной цели существенна. Положение кривых на графике рис. 12 позволяет утверждать, что при оптимальных параметрах метод Е-импульса сохраняет возможность различения двух целей вплоть до отношений сигнал-шум порядка 0 дБ, что является наилучшим результатом по сравнению со всеми прочими возможными длительностями секций Δ и порядками полиномов Q. Из этого следует, что выбор оптимальной длительности секции Е-импульса способен существенно увеличить различающую способность в присутствии шума.

 

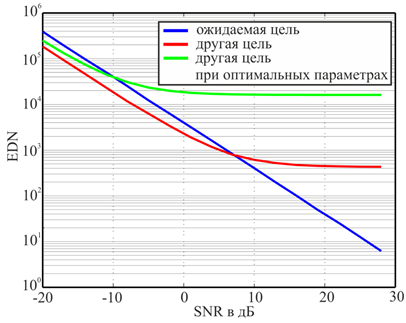
Рис. 12. Зависимость качества идентификации от отношения сигнал-шум

5. Заключение

В настоящей работе были рассмотрены теоретические основы метода Е‑импульса, использующего в качестве признака для распознавания радиолокационных объектов наборы полюсов – комплексных частот, описывающих резонансы облучаемых объектов. Процедура синтеза сигнала Е‑импульса, имеющего полиномиальную секционную структуру, состоит в формировании системы линейных уравнений, имеющей единственное решение, на основе необходимых условий, формулируемых относительно набора полюсов, и условий гладкости и непрерывности. Было показано, что совокупность таких условий накладывает жесткую связь на количество секций при известном количестве полюсов и желаемом порядке полиномов.

В работе также рассмотрена структурная схема системы распознавания целей на основе интегрального скалярного параметра – дискриминационного числа Е-импульса. В качестве примера на её основе было проведено моделирование распознавания двух целей с известными наборами полюсов. Была оценена различимость целей в зависимости от отношения сигнал-шум в предположении о присутствии аддитивного гауссовского шума в принятом сигнале.

Проведенное моделирование показало, что дискриминационные свойства посекционного Е‑импульса существенно зависят от длительности секции и слабо зависят от порядка полиномиальной функции. Так, существуют  оптимальные значения этих параметров, использование которых обеспечивает максимум дискриминационного числа, что позволяет добиться распознавания при меньших отношениях сигнал-шум и, таким образом, расширить границы практической применимости метода.

Литература

1. C.E. Baum, The singularity expansion method // Transient Electromagnetic Fields, 129-179, L.B.Felsen (ed.), New York, 1976.

2. M.A. Morgan, Singularity expansion representations of fields and currents in transient scattering // IEEE Trans. Antennas Propagat., vol. 32, no.5, pp. 466-473, May 1984.

3. M. Hurst and R. Mittra, Scattering center analysis via Prony's method // IEEE Trans. on Antennas Propagat., vol. 35 (8), pp. 986-988, Aug. 1987.

4. P. Ilavarasan, E. Rothwell, K.M. Chen, and D.P. Nyquist, Natural resonance extraction from multiple data sets using a genetic algorithm // IEEE Trans. Antennas Propagat., vol. 43, no.8, pp. 900-904, Aug. 1995.

5. T.K. Sarkar, O. Pereira, Using the matrix pencil method to estimate the parameters of a sum of complex exponentials // IEEE Antennas Propagat. Magazine, vol. 37 (1), pp. 48-55, Jan. 1995.

6. E.J. Rothwell, D.P. Nyquist, K.M. Chen, and B. Drachman, Radar target discrimination using the extinction-pulse technique // IEEE Trans. Antennas Propag., vol. 33, no. 9, pp. 929-936, Sep. 1985.

7. E.J. Rothwell, Radar target discrimination using the extinction-pulse technique, Ph.D. dissertation, Michigan State University, 1985.

8. I. Gerst and J. Diamond, The elimination of intersymbol interference by input signal shaping  // Proceedings of the IRE, pp. 1195-1203, July, 1961.

9. E. Rothwell, K.M. Chen, and D.P. Nyquist, Frequency domain E-pulse synthesis and target discrimination // IEEE Trans. Antennas Propagat., vol. AP-33, pp. 445-450, Apr. 1985.

10. D. Blanco, D.P. Ruiz, E. Alameda-Hernández, and M.C. Carrión, Extinction pulses synthesis for radar target discrimination using β-splines, new E-pulse conditions // IEEE Trans. Antennas Propag., vol. 54, no. 5, May 2006.

11. M.C. Carrión, A. Gallego, J. Portí, and D.P. Ruiz, Subsectional-polynominal E-pulse synthesis and application to radar target discrimination // IEEE Trans. Antennas Propagation, vol. AP-41, no. 9, September 1993.

12. D.P. Nyquist, E.J. Rothwell, L. Webb, B. Drachman, Radar target discrimination by convolution of radar return with extinction-pulses and single-mode extraction signals // IEEE Trans. Antennas Propagation, vol. 34, no. 7, July 1986.

13. E. Rothwell, P. Ilavarasan, and J. Ross, Perfomance of an automated radar target discrimination scheme using E-pulses and S-pulses // IEEE Trans. Antennas Propagation, vol. 41, no. 5, May 1993.

14. D. Blanco, D.P. Ruiz, E. Alameda-Hernández, and M.C. Carrión, An asymptotically unbiased E-pulse-based scheme for radar target discrimination // IEEE Trans. Antennas Propagation, vol. 52, no. 5, May 2004.

15. Филимонова Д.В., Шевгунов Т.Я., Оптимизация параметров посекционного полиномиального е-импульса при решении задачи различения целей в сверхширокополосной радиолокации // VIII Всероссийская конференция научно-техническая конференция «Радиолокация и радиосвязь», ИРЭ РАН, 24-26 ноября 2014, стр. 52–56.