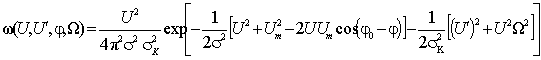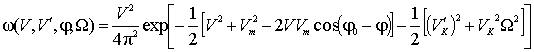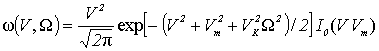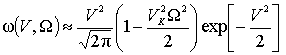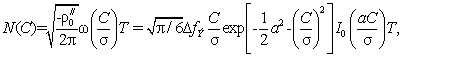УДК 621.391.82.016.35

ОЦЕНКА ОТНОШЕНИЯ СИГНАЛ/ШУМ В СПУТНИКОВЫХ СИСТЕМАХ СВЯЗИ

 

А. А. Силантьев ^1,2, В. Г. Патюков ², Е. В. Патюков ², В. А. Шатров ^1,2

¹ ОАО «Информационные спутниковые системы» им. М.Ф. Решетнева

² Институт инженерной физики и радиоэлектроники, Сибирского Федерального Университета

Статья получена 27 февраля 2015 г.

 

Аннотация. Рассмотрена возможность использования нового метода оценки отношения сигнал/шум, основанного на анализе статистических характеристик выбросов случайных процессов аддитивной смеси сигнала и шума, для повышения точности и помехоустойчивости работы канала связи, а так же для оптимизации командно-измерительной системы спутниковой связи.

Ключевые слова: Командно-измерительная система, отношение сигнал/шум, характеристики выбросов случайных процессов.

Abstract: Considered the problems of research of a new method for estimating signal / noise ratio, based on the analysis of the statistical characteristics of the peaks of random processes used to improve the accuracy and noise immunity of the channel of communication, as well as to optimize the hardware command-measuring satellite communications systems.

Key words: command-measuring system, the ratio signal/noise, characteristics of random processes.

 

Введение

При решении текущих задач в космической связи используются космические аппараты (КА), в системе командного управления которых выделяют бортовой (БС) и наземный (НС) сегменты управления. Обмен информацией между которыми обеспечивает командно-измерительная система (КИС), используя командную радиолинию. КИС решает задачи приёма командно-программной информации от наземной станции, передачи телеметрической информации с КА на наземные станции и измерение текущих навигационных параметров.

КИС имеют ряд особенностей, влияющих на построение систем спутниковой связи, к которым следует отнести [1]:

1. КИС должны обеспечивать надёжное управление искусственными спутниками земли в различных режимах его полёта.

2. Источники передаваемой по радиолиниям КИС информации находятся как на борту искусственного спутника земли, так и на НС.        

3. КИС должны обеспечивать повышенную достоверность передаваемой на искусственный спутник земли информации с обязательным квитированием факта её прохождения.

Радиолиния КИС состоит из двух участков: НС – КА и КА – НС. На этих участках сигнал подвергается воздействию различных помех, что в результате влияет на отношении сигнал/шум и качество работы устройств КИС [2]. Если требуемое отношение сигнал/шум не обеспечено, то нарушаются энергетические характеристики и уменьшается надёжность работы командной радиолинии. Поэтому одной из важнейших задач работы КИС является оценка её помехоустойчивости, так как от этого зависит качество обмена информацией между БС и НС.

2. Метод оценки отношения сигнал/шум на основе статистических характеристик выбросов случайных процессов

Для определения особенностей изменения параметров аддитивной смеси обратимся к простейшей частной модели суммирования двух гармонических колебаний с близкими частотами, которую представим в виде х(t)=s₁(t)+s₂(t)=U₁ cosω₀t+U₂ cosω₁t. Рассматриваемую модель для удобства оценки степени взаимосвязи между исследуемыми параметрами преобразуем к виду

х(t)=U₁ cosω₀t+U₂ cos[(ω₀+∆ω)t]=(U₁ +U₂ cos∆ωt)cosω₀t – U₂ sin∆ωt sinω₀t.

Такое представление позволяет рассматривать аддитивную смесь двух гармонических колебаний с близкими частотами в виде суммы двух квадратурных колебаний, амплитуды которых изменяются также по гармоническому закону с частотой расстройки ∆ω= ω₁–ω₀. Эту простейшую модель аддитивной смеси представим в виде компактной записи суммарного процесса

х(t)=U(t)cos(ω₀t+φ(t)), где  – огибающая исследуемой аддитивной смеси, а фаза равна φ(t)=arctg(U₂₁sin∆ωt/(1+ U₂₁cos∆ωt));  – нормированная амплитуда сигнала  относительно амплитуды сигнала . Следует отметить, что такое значение фаза будет иметь при . В других случаях при , с учётом ограничения реального значения фазы интервалом [0, 2π], в выражении для фазы следует добавлять π при  и –π при .

Результирующий сигнал в таком представлении является сигналом с амплитудной и угловой модуляцией и может иметь широкий спектр. Характер развития результирующего сигнала во временной области существенно зависит от параметра . Так, на рис. 1 приведён график поверхности изменения огибающей суммарного процесса  при различных , а на рис. 2 даны сечения графика поверхности в зависимости от нормированного времени.

Из анализа графиков, представленных на рисунках, следует, что резкие изменения огибающей соответствуют значению . При этом значении  на рис. 3 приведён график развития процесса  в пределах периода изменения огибающей с характерной для этих условий фазовой манипуляцией.

Особенности метода оценки отношения сигнал/шум предварительно рассмотрим на примере анализа аддитивной смеси манипулированного сигнала и узкополосного дифференцируемого стационарного нормального случайного процесса

,

где , , - амплитуда, угловая частота и начальная фаза сигнала ,  - манипулирующая последовательность,  и  - огибающая и фаза случайного процесса .

 

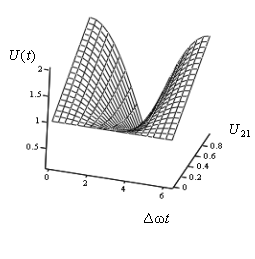
Рис. 1. Зависимость огибающей суммарного процесса

от исследуемых параметров. 

В общем случае анализа рассматриваемой аддитивной смеси достаточно полное вероятностное описание характера изменения случайных параметров может быть получено на основе известной информации о совместной многомерной плотности распределения огибающей аддитивной смеси, фазы и их производных. В часто встречающемся на практике случае отсутствия расстройки между частотой сигнала  и центральной частотой энергетического спектра квазигармонического дифференцируемого гауссовского шума ξ(t), такая плотность распределения получена в [3]:

      ,          (1)

где  и  - дисперсии процесса ξ(t) и его квадратурных составляющих производных, Ω(t)=φ^'(t) – случайная частота, определяемая через производную фазы аддитивной смеси и характеризующая скорость её изменения.

Выполнив нормировки в (1) относительно дисперсий, получим

         ,      (2)

где ; ; ; .

Проинтегрировав (2) по «лишним» переменным, получим другие совместные распределения, которые можно использовать для исследования особенностей исследуемых параметров и оценки их влияния на работу систем связи. Так, совместную плотность распределения огибающей аддитивной смеси и случайной частоты, получим в результате интегрирования

,

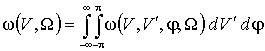тогда совместное распределение огибающей и случайной частоты будет равно:

            ,                        (3)

где  - модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

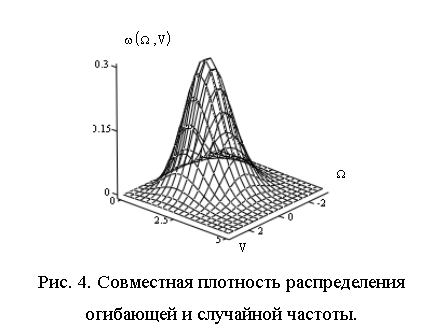
Результаты расчётов, выполненных по (3), приведены на рис. 4, где представлен график совместной плотности распределения , при значениях нормированных параметров  и , то есть когда амплитудные значения гармонического сигнала соизмеримы со среднеквадратическим значением случайного процесса ξ(t) и квадратурной составляющей производной этого процесса. Из анализа графика можно сделать выводы о статистической зависимости между переменными  и .

 Совместное распределение (3) допускает аппроксимацию при малых (<<1) и больших (>>1) аргументах, если воспользоваться асимптотическими представлениями функций Бесселя мнимого аргумента [5]. Так при <<1, ограничиваясь двумя слагаемыми разложений экспоненты и функции Бесселя при малых аргументах, получим:

,

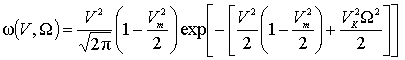а, учитывая наложенные условия на параметры распределения, придём к более простому выражению

,

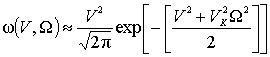которое с учётом того, что и <<1, можно привести к виду

                                  .                                (4)

Анализ (4) показывает, что в формировании совместного распределения  при <<1 участвуют различные функции, образуя в итоге модифицированную функцию Рэлея.

При >>1 для функции Бесселя допустимо приближённое равенство [5]

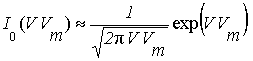
и совместное распределение (3) приводится к виду:

,

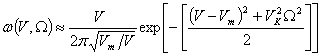которое в области значений  можно представить выражением:

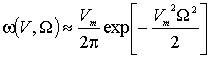                                                 .                                              (5)

Эта зависимость при фиксированных значениях  представляет собой функцию, аппроксимирующую совместное распределение (4). При фиксированных W, выражение (5) аппроксимирует совместное распределение функцией Рэлея в зависимости от .

Полученные результаты иллюстрируются графиком поверхности, представленным на рис. 5 и позволяют – исследовать динамику преобразования плотности распределения Рэлея в Гауссово распределение, охарактеризовать наиболее вероятные значения огибающей и оценить интенсивность разброса.

 

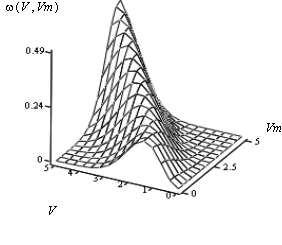
Рис. 5. Динамика преобразования плотности распределения

Рэлея в Гауссово распределение.

Одним из методов нахождения отношения сигнал/шум в системах связи является оценка вероятностных характеристик выбросов случайных процессов, основанном на использовании статистического аппарата анализа, позволяющего получить высокоточные результаты измерений в условиях интенсивного воздействия помех, так как определение среднего числа положительных выбросов в единицу времени, позволяет найти отношение сигнал/шум [3, 4].

Для оценки отношения сигнал/шум, необходимо использовать информацию о числе выбросов аддитивной смеси , превышающих определённый уровень. Достаточно полное вероятностное описание характера изменения выбросов может быть получено на основе известной информации о совместной плотности распределения (2), исследуемой аддитивной смеси. При некоррелированных отсчётах исследуемого случайного процесса среднее число положительных выбросов N в единицу времени, можно найти по совместной плотности распределения, а полученный результат представить в виде [4]:

                               (6)

где – вторая производная от функции корреляции аддитивной смеси гармонического сигнала и узкополосного случайного процесса, С – уровень ограничения, T – время анализа,  – ширина энергетического спектра шума в рассматриваемой системе  и  – отношение сигнал/шум.

Из (6) следует, что интенсивность и характер зависимости среднего числа выбросов огибающей узкополосного случайного процесса от уровня ограничения С определяется по результатам изменения соответствующей плотности вероятности огибающей ω(С/σ), зависящей от отношения сигнал/шум.

Значение уровня ограничения С, обеспечивающее минимальную дисперсию числа превышений, находиться по известным правилам:

     , 

 

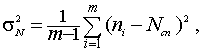
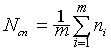где m – количество реализаций аддитивной смеси x(t),  – количество превышений уровня ограничения в каждой реализации,  – среднее число пересечений.

В таблице 1 приведены результаты расчётов значений дисперсии числа пересечений аддитивной смеси x(t) (исследования проводились для сигнала с амплитудой равной 1 В), при трех значениях уровня ограничения С (0, 0.5 и 1) и времени наблюдения T, равном 2, 1 и 0.5 мс. Данные получены на основе анализа результатов 10 реализаций для каждого времени наблюдения.

Как следует из таблицы 1, минимальная дисперсия числа пересечений достигается при значении порога, равном 1 В. Следует отметить, что выполнив исследования для сигналов с амплитудами от 2 до 10 В, установлено, что минимальная дисперсия числа пересечений достигается при пороге, равном амплитуде исследуемого сигнала и характеризуется графиком на рис. 6.

 Таблица 1.

С	T = 2 мс		С	T = 1 мс		С	T = 0.5 мс
0 В	24.5	6.84	0 В	12.4	3.21	0 В	6.36	1.31
0.5 В	13.8	4.86	0.5 В	7	2.9	0.5 В	3.64	1.71
1 В	0.28	0.281	1 В	0.12	0.16	1 В	0.08	0.074

 

На рисунке приведён график поверхности среднего числа положительных выбросов, в зависимости от отношения сигнал/шум при ширине энергетического спектра шума, равной 1 МГц.

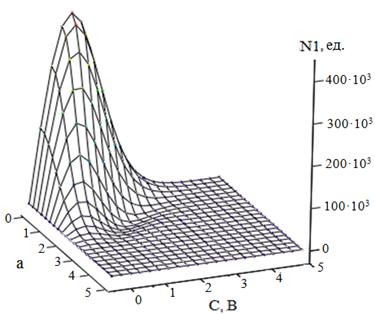
Рис. 6. График поверхности, характеризующей зависимость среднего числа

положительных выбросов от отношения сигнал/шум.

Анализируя график можно отметить, что при отношении сигнал/шум, равному нулю (а=0, то есть при отсутствии сигнала и соответствующем значении порога), среднее количество выбросов принимает максимальное значение. При увеличении отношения сигнал/шум среднее количество выбросов уменьшается, и достигает минимума при a ≈ 3.

3. Реализация устройств оценки отношения сигнал/шум на основе анализа характеристик выбросов случайных процессов

Из проведённых исследований анализа характера изменения огибающей рассматриваемой аддитивной смеси и оценки её вероятностных характеристик следует, что определив среднее количество выбросов огибающей можно выполнить аппаратную оценку отношения сигнал/шум.

Упрощённая структура устройства измерения отношения сигнал/шум на основе анализа статистических характеристик выбросов случайных процессов  приведена на рис. 7.

Рис. 7. Вариант реализации устройства оценки отношения сигнал/шум по выбросам случайных процессов.

В соответствии со структурной схемой, в приёмнике КИС формируется аддитивная смесь x(t), которая поступает на анализатор огибающей, где устанавливается требуемый уровень ограничения. Сформированные импульсы, пропорциональные числу выбросов, подсчитываются счётчиком. Конечный результат формируется в блоке обработки и индикации, где с учётом (6), вычисляется реальное отношение сигнал/шум.

4. Выводы

Рассмотренные особенности изменения огибающей аддитивной смеси и метод оценки отношения сигнал/шум, основанный на анализе числа выбросов, превышающих заданный уровень, позволяют вести оперативный контроль измеряемых параметров сигналов КИС. Результаты полученных оценок можно использовать для повышения надёжности работы и помехоустойчивости КИС – управляя мощностью передающего устройства, оптимизируя методы обработки используемых сигналов, а также регулируя характеристики антенных систем.

Литература

1.     Патюков В.Г., Рябушкин С.А., Шатров В.А. Командно-измерительная система космического аппарата на геостационарной орбите //XVII всероссийская НТК «Современные проблемы радиоэлектроники» – г. Красноярск, СФУ, 2014 г. – С. 273.

2.     Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М., Теория передачи сигналов. – М.: Радио и связь, 2001 г. – 368 с.

3.     Тихонов, В.И. Нелинейные преобразования случайных процессов /В.И. Тихонов. – М.: Радио и связь, 1986. – 259 с.

4.     Тихонов В.И. Выбросы случайных процессов. – М.: Наука, 1970 г. – 392 с.

5.     Корн, Г. Справочник по математике для научных работников и инженеров /Г. Корн, Т. Корн. - М.: Наука, 1978. - 831 с.