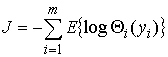УДК 681.513.6                                                                             

ПРИМЕНЕНИЕ АЛГОРИТМА СЛЕПОГО РАЗДЕЛЕНИЯ ПОМЕХ НА ОСНОВЕ МИНИМИЗАЦИИ ВЗАИМНОЙ ИНФОРМАЦИИ В ОПОРНЫХ КАНАЛАХ МНОГОКАНАЛЬНОГО АДАПТИВНОГО КОМПЕНСАТОРА

 

А. Е. Манохин

Институт радиоэлектроники и информационных технологий-РТФ УрФУ им. первого Президента РФ Б.Н.Ельцина,
кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург

Статья поступила в редакцию 3 декабря 2015 г., после доработки – 7 марта 2016 г.

 

Аннотация. В работе решается задача предварительного разделения помех в опорных каналах адаптивного многоканального компенсатора на основе алгоритма минимизации взаимной информации. В результате этого, во-первых, увеличивается скорость сходимости адаптивного алгоритма наименьших квадратов, а во-вторых, разделяются помехи, имеющие не только разные задержки и уровни, но и подвергнутые различным линейным преобразованиям в канале распространения. При этом выигрыш в скорости сходимости при использовании алгоритма слепого разделения на основе минимизации взаимной информации  составляет не менее 28 раз.

Ключевые слова: слепое разделение сигналов, многоканальный адаптивный компенсатор, алгоритм слепого разделения на основе минимизации взаимной информации, скорость сходимости.

Abstract. In the work the problem of multichannel adaptive cancelling disturbances with their preliminary separation in reference channels is decided. A kind of the canceller is an application of blind separation algorithm by minimizing mutual information. As a result, first, convergence rate is increased, and second, disturbances separate even if to be exposed by different linear transformations in a channel. The gain of convergence rate equals not less than 28 times.

Key words: blind sources separation, multichannel adaptive canceller, algorithm by minimizing mutual information, convergence rate.

 

Введение

В [1,2] решалась задача повышения скорости сходимости адаптивного алгоритма наименьших квадратов (МНК) при многоканальной адаптивной компенсации помех с использованием предварительного слепого разделения помех в опорных каналах с помощью алгоритмов Жуттена-Эро и DUET.

Эти алгоритмы имеют следующие особенности: алгоритм Жуттена-Эро работоспособен при когерентности однотипных помех в опорном канале приема, алгоритм DUET — если помехи, приходящие в опорный канал, имеют различные задержки, но претерпевают одинаковые линейные преобразования в канале распространения (т.е. сворачиваются с одной и той же импульсной характеристикой). Если помехи в каналах проходят различные пути распространения до прихода в точку приема, то указанные алгоритмы неработоспособны.

Постановка задачи                                                                                              

Необходимо найти тип нейронной сети и синтезировать «слепой» алгоритм, учитывающий при разделении импульсные характеристики каналов, по которым распространяются разделяемые помехи в опорном канале многоканального адаптивного компенсатора.

 

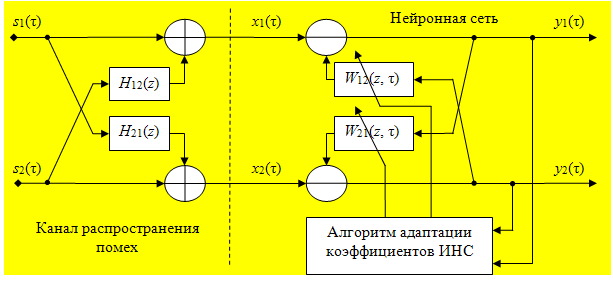
Рис. 1. Рекуррентная нейронная сеть с обратными связями в виде фильтров.

 

Представим коэффициенты смешивания фильтрами с коэффициентами передачи H_i(z) (рис. 1), которые моделируют канальные импульсные характеристики. Тогда в искусственной нейронной сети (ИНС) в цепях обратной связи коэффициенты необходимо заменить фильтрами с коэффициентами передачи W_i(z) (рис. 1).

В качестве критерия разделения в [3,4,5] предлагается использовать меру Кульбака-Лейблера. Эта мера показывает близость двух распределений. Если распределения полностью совпадают, то мера Кульбака-Лейблера принимает нулевое значение. Частным случаем этой меры является критерий минимума взаимной информации — самым простой в реализации и обладающий хорошими свойствами сходимости [3].

Взаимная информация выходов нейронной сети может быть выражена:

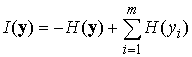                                                                                    (1)

где H(y_i) — энтропии оцениваемых после разделения сигналов с выходов y_i;

      H(y) — взаимная энтропия процессов на выходах нейронной сети;

       m — число выходов нейронной сети (количество разделяемых процессов).

Внимательно анализируя (1) и учитывая суть слепого разделения сигналов, можно заметить, что при полном их разделении на соответствующих выходах нейронной сети будут присутствовать только процессы с искомыми распределениями, а взаимная информация по всем выходам будет равна нулю и соответственно сумма их энтропий будет минимальна, что эквивалентно минимизации функционала  [5]:

                                               ,                                         (2)

где Θ_i(y_i) — функции плотности вероятности разделяемых процессов;

      E — оператор усреднения.

Запишем сигналы выходов рекуррентной нейронной сети (рис. 1) в векторно-матричной форме следующим образом:

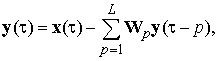                                                                            (3)

где W_p — p-ая разделяющая матрица W, имеющая нулевые диагональные элементы (w_ii=0) и зависящая от сдвига на p отсчетов суммируемых сигналов в цепи обратной связи ИНС; L — число весовых коэффициентов фильтров в цепи обратной связи нейронной сети; τ — время, измеряемое в отсчетах.

Дифференциал функционала (2):

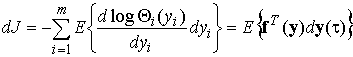                            ,                      (4)

где f(y) — вектор-столбец производных от функций логарифмической плотности вероятности 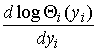 (функций активации).

 

Из выражения (3) найдем дифференциал вектора выходных сигналов по разделяющей матрице:

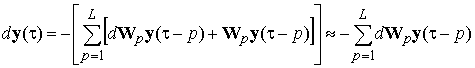                .          (5)

Упрощение выражения (5) связано с тем, что на малые изменения выходных сигналов влияют только малые изменения элементов матриц W_p.

Обычный градиентный поиск элементов разделяющих матриц приводит к следующему выражению:

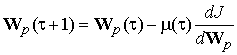                                        ,                                  (6)

где μ(τ) — коэффициент адаптации алгоритма, который также может зависеть от времени.

Градиент функционала (2) с учетом выражений (4) и (5) равен:

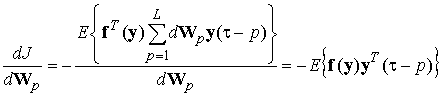                    .             (7)

Усреднение заменим на скользящее среднее и получаем алгоритм градиентного поиска коэффициентов p-разделяющих матриц:

                                       ,                                (8)

где  — матрица взаимной корреляции функции активации от выходных сигналов и выходных сигналов ИНС; μ₀ — произвольно выбираемый коэффициент меньше единицы.

Расчет скорости сходимости без предварительного разделения помех

Время сходимости без предварительного разделения помех (для смеси из двух процессов) определяется по постоянной времени обучающей кривой для многоканального адаптивного фильтра через отношение собственных значений корреляционной матрицы помех [2]:

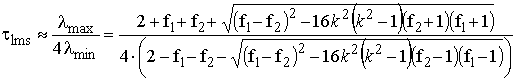                   (9)

где f₁ и f₂ — значения первых отсчетов нормированных автокорреляционных функций разделяемых процессов; k — СКО помех в каналах (k<1).

Необходимо отметить, что значение первого отчета нормированных автокорреляционных (по крайней мере, монотонно убывающих) функций  процессов f₁ и f₂ влияют на их эффективную ширину полосы: чем оно меньше, тем шире полоса процесса.

На рис. 2 изображены зависимости скорости адаптации фильтров от соотношения помех на опорных входах компенсатора при разных значениях первых отсчетов нормированных автокорреляционных функций, которые показывают, что наихудший случай для сходимости — два процесса с более узкой полосой, наилучший — два процесса с более широкой полосой.  

 

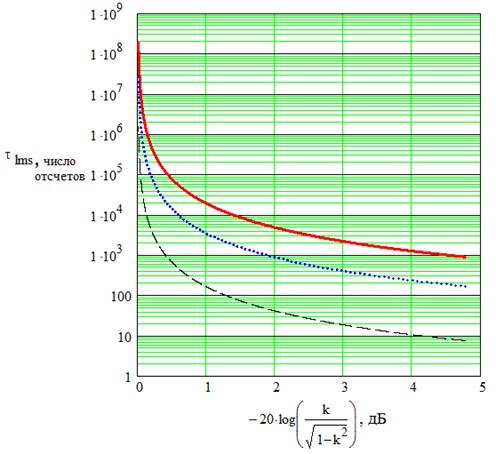
Рис. 2. Зависимости скорости адаптации фильтров от соотношения помех на опорных
входах компенсатора при разных значениях автокорреляционных функций:
f₁=0.995, f₂=0.981 (сплошная), f₁=0.981, f₂=0.368 (точечная), f₁=0.368, f₂=0.36 (штриховая)

Компьютерное моделирование алгоритма слепого разделения помех на основе минимизации взаимной информации

Алгоритм (8) представлен в среде Mathcad на рис. 3 (N — объем выборки, L — размеры фильтров в цепях обратной связи ИНС). В качестве функции активации в [6] рекомендовано для процессов с отрицательным эксцессом использовать функцию f(y)=y³_, для положительного эксцесса — функцию f(y)=tanh(y).

 

Рис. 3. Программная реализация алгоритма (8)
 

Для разделения моделируется аддитивная смесь из двух процессов с параметрами, отображенными в таблице 1.
 

Таблица 1. Параметры помех, действующих в опорном канале

№ смеси	Условное обозначе-ние процессов в смеси	Название (объем выборки)	Тип процесса	Выражение для формирования помехи
1	ФМн1	Фазоманипулированный  меандром гармонический процесс (65536 отсчетов)	Детермини-рованный	Imp1(τ) — меандр с периодом 1024 отсчета
	ФМн2			Imp2(τ) — меандр с периодом 512 отсчетов
2	ФМ (БГШ)	Фазомодулированный белым гауссовым шумом гармонический процесс (65536 отсчетов)	Случайный	n(τ) — белый  гауссов шум
	ФМн	Фазоманипулированный  меандром  гармонический процесс (65536 отсчетов)	Детермини-рованный	Imp2(τ) — меандр с периодом 512 отсчетов
3	ФМ1 (БГШ)	Фазомодулированный  белым гауссовым шумом гармонический процесс (65536 отсчетов)	Случайный	n1(τ) — белый  гауссов шум
	ФМ2 (БГШ)			n2(τ) — белый  гауссов шум

 

Соотношение мощностей помех в смеси q_in=0.5 дБ. В качестве передаточных функций канала использовался КИХ-фильтр с 32 весовыми коэффициентами и с экспоненциальными импульсными характеристиками:

                                  ; .                         (10)

Результаты компьютерного моделирования алгоритма (8) отображены на рисунках 4–6 и в таблице 2.

 

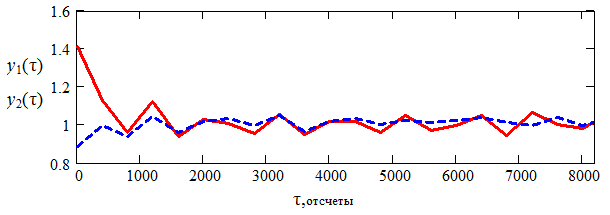
Рис. 4. Зависимость дисперсии выходных сигналов нейронной сети от времени (для смеси №1)
 

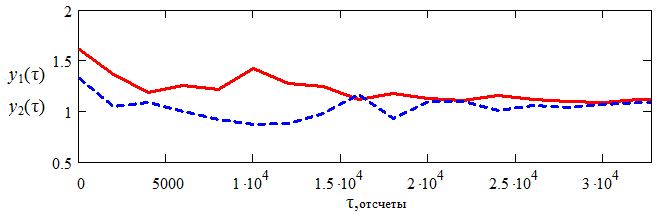
Рис. 5. Зависимость дисперсии выходных сигналов нейронной сети от времени (для смеси №2)
 

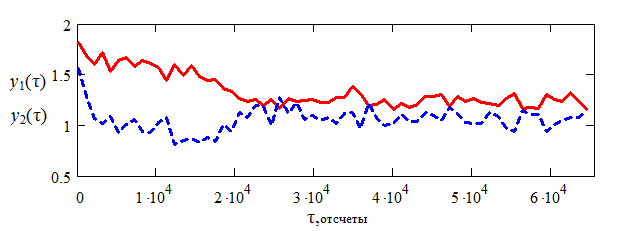
Рис. 6. Зависимость дисперсии выходных сигналов нейронной сети от времени (для смеси №3)

 

Таблица 2. Результаты моделирования алгоритма слепого разделения на основе минимизации взаимной информации

№ смеси	Процессы в смеси/ значение первого отсчета АКФ	Отношение мощностей процессов после разделения qout, дБ	Время сходимости алгоритма слепого разделения τbss, отсчет
1	ФМн1/f1=0.995; ФМн2/f2=0.981	ФМн1: qout =17.1 дБ; ФМн2: qout =17.0 дБ	2500
2	ФМн/f1=0.981; ФМ (БГШ)/f2=0.368	ФМн:   qout = 7.8 дБ; ФМ:     qout = 10.2 дБ	>20000
3	ФМ1 (БГШ)/f1=0.368; ФМ2 (БГШ)/f2=0.36	ФМ1:   qout = 4.7 дБ; ФМ2:   qout = 5.6 дБ;	>35000

 

Анализ результатов разделения в таблице 2 показывает, что наилучшее разделение алгоритмом на основе минимизации взаимной информации выполняется для аддитивной смеси фазоманипулированных меандром сигналов.

При этом, в ходе эксперимента установлено, что чем более узкополосными являются сигналы в смеси, тем быстрее сходимость алгоритма слепого разделения и тем эффективнее разделение сигналов.

В таблице 3 отображены результаты расчета выигрыша в скорости сходимости многоканального компенсатора при использовании предварительного разделения помех алгоритмом на основе минимизации взаимной информации. Выигрыш вычисляется по формуле:

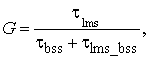                                                                                          (11)

где  τ_lms — время сходимости алгоритма наименьших квадратов без  предварительного разделения помех в опорных каналах (определяется по рис. 2 или ф. 9, подставляя q_in= 0.5 дБ);

         τ_bss — время сходимости алгоритма слепого разделения сигналов на основе минимизации взаимной информации (берется из таблицы 2);

         τ_{lms_bss} — время сходимости алгоритма наименьших квадратов c предварительным разделением помех в опорных каналах (определяется по рис. 2 или ф. 9, подставляя q_out из таблицы 2).
 

Таблица 3. Расчет выигрыша в скорости адаптации фильтров трехканального адаптивного компенсатора
при использовании предварительного разделения помех в опорных каналах

Смесь процессов	Значение первого отсчета АКФ	τlms (ф.9)	τbss (табл.2)	τlms_bss	G (ф.11)
ФМн1 ФМн2	0.995 0.981	75845	2500	141	28.7
ФМн ФМ (БГШ)	0.981 0.368	13716	20000	32	0.68
ФМ1 (БГШ) ФМ2 (БГШ)	0.368 0.36	647	35000	7	0.018

 

Таким образом, выигрыш в скорости сходимости приходится на смесь из двух фазоманипулированных сигналов и составляет почти 29 раз, что демонстрирует преимущество предварительного разделения. Если хотя бы один сигнал более широкополосный по сравнению с другим, то целесообразность применения предварительного разделения помех (при соотношении их мощностей в опорных каналах q_in=0.5 дБ) отсутствует.

Покажем, в каком диапазоне значений должно находиться соотношение мощностей помех в опорных каналах q_in, чтобы выигрыш от предварительного разделения широкополосных помех, по крайней мере, существовал, т.е. был больше единицы. Предположим, что отношение мощностей помех после разделения и скорость сходимости алгоритма разделения останутся на том же уровне, как и в предыдущих расчетах. Построим зависимости выигрыша G от отношения мощностей помех до их разделения q_in (рис. 7), используя формулы (9) и (11).

Анализируя рисунок 7 можно отметить, что выигрыш от предварительного разделения фазоманипулированного меандром и фазомодулированного белым гауссовым шумом сигналов получается при отношении их мощностей в опорных каналах до разделения менее 0.42 дБ, а фазомодулированных белым гауссовым шумом сигналов с разными несущими частотами — менее 0.07 дБ.

 

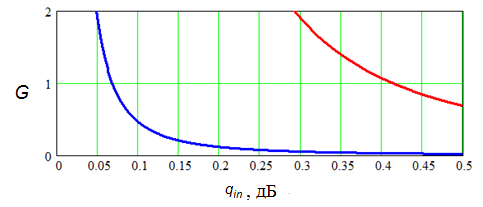
Рис. 7. Зависимости выигрыша в скорости сходимости при использовании предварительного разделения помех
(смесь №2 — красная линия; смесь №3 — синяя линяя) в опорных каналах от отношения их мощностей до разделения

 

Выводы

1.     Использование алгоритма слепого разделения на основе минимизации взаимной информации позволяет увеличить скорость сходимости алгоритма адаптации наименьших средних квадратов в многоканальном адаптивном компенсаторе не менее чем в 28 раз, что значительно превосходит модифицированный алгоритм Жуттена-Эро и алгоритм DUET (при том же соотношении мощностей помех в опорных каналах 0.5 дБ).

2.     Установлено, что выигрыш в предварительном разделении помех тем больше, чем меньше ширина полосы помех, действующих в опорных каналах.

3.  Дополнительное преимущество алгоритма слепого разделения на основе минимизации взаимной информации перед алгоритмами DUET и Жуттена-Еро состоит в том, что разделяются помехи, имеющие не только разные задержки и уровни, но и подвергнутые различным линейным преобразованиям в канале распространения.

 

Литература

1. Манохин А.Е. Многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах // Журнал радиоэлектроники [электронный журнал].  2014. №10. Режим доступа: http://jre.cplire.ru/jre/oct14/4/text.pdf.

2. Манохин А.Е. Многоканальная адаптивная компенсация узкополосных помех с их предварительным слепым разделением в опорных каналах // Журнал радиоэлектроники [электронный журнал]. 2015. №11. Режим доступа: http://jre.cplire.ru/jre/nov15/7/text.pdf.

3. J.F. Cardoso, “Blind signal separation: statistical principles,” Proceeding of the IEEE, vol. 10, no. 9, pp.2009–2025, 1998.

4. Цифровая обработка сигналов и изображений в радиофизических приложениях. / Под ред. В.Ф. Кравченко. — М. : ФИЗМАТЛИТ, 2007. — 544 с.  

5. A.Cichoki and S.Amari, Adaptive Blind Signal and Image Processing: Learning Algorithms and Applications, John Wiley & Sons, 2002.

6. S. Amari, S. Douglas, A. Cichocki, H. Yang, “Multichannel blind deconvolution and equalization using the natural gradient,” Proc. 1st IEEE Workshop Signal Processing Adv. Wireless Commun., Paris, France, pp. 101–104, Apr. 1997.