| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5 , 2000 |
ЭФФЕКТИВНОСТЬ
ПОЛЯРИЗАЦИОННЫХ РАДИОЛОКАТОРОВ В ЗАДАЧЕ
ОБНАРУЖЕНИЯ СТАБИЛЬНЫХ ЦЕЛЕЙ НА ФОНЕ
ПАССИВНЫХ ПОМЕХ
Сибирский Физико-технический институт, г. Томск
Получена 12 мая 2000 г.
Исследуются вопросы статистического моделирования радиолокационного канала перспективных РЛС, использующих сигналы со сложной поляризационной структурой для задач селекции стабильных целей на фоне пассивных помех. Наиболее эффективным показателем работы систем являются её рабочие характеристики. Использование параметров, полученных в результате измерения матрицы рассеяния или её инвариантов, обеспечивает более устойчивые к условиям радиолокационного наблюдения алгоритмы обнаружения, чем при использовании лишь измерений ЭПР объектов.
Предложена вероятностная модель радиолокационного канала, имеющего одноканальную структуру приёмо-передающего тракта и позволяющего формировать инвариантный - степень анизотропии (m ) и динамический – угол ориентации собственного базиса цели относительно измерительного (a ) поляризационные параметры. На примере предложенных вероятностных моделей исследуются вопросы повышения эффективности поляризационных РЛС.Введение.
В перспективных радиолокационных системах (ПРЛС), использующих сигналы с поляризационной структурой (ПС), селекция стабильных целей на фоне пассивных помех представляет собой достаточно сложную задачу. Для решения задач обнаружения и оценки эффективности ПРЛС используются статистические методы, основанные на применении вероятностных моделей суммарного поля, обусловленных наличием отражений от цели и фона. Вероятностные модели некоторых поляризационных параметров радиолокационных сигналов достаточно хорошо изучены в работах [1, 2]. Однако в силу того, что может быть предложено большое количество конкретных систем обработки сигнала, использующих различные поляризационные параметры, то имеется необходимость анализа характеристик конкретной системы, наилучшей в отношении определенного критерия. Наиболее эффективным показателем работы систем являются её рабочие характеристики, которые могут быть получены на основе использования вероятностных моделей используемых параметров. Использование параметров, полученных в результате измерения матрицы рассеяния (МР) или её инвариантов, обеспечивает более устойчивые к условиям радиолокационного наблюдения алгоритмы обнаружения, чем при использовании лишь измерений ЭПР объектов. Упомянутые характеристики можно использовать при решении всех видов задач: обнаружения, различения, распознавания образов, селекции и т.д. Использование инвариантных и динамических параметров МР в задачах повышения эффективности ПРЛС связано с применением сигналов с поляризационной структурой, позволяющих производить измерения этих параметров. В данной ситуации необходимо переходить от статистической модели рассеянного целью радиолокационного сигнала к модели поляризационных параметров цели.Одно из перспективных направлений повышения эффективности алгоритмов обнаружения целей и распознавания образов связано с использованием таких параметров МР, как поляризационной степени анизотропии (m ) и угла ориентации собственного базиса цели относительно измерительного (a
). Интерес к этим параметрам обусловлен ещё и тем, что известны алгоритмы функционирования одноканальных РЛС на излучение и приём, позволяющие формировать m и a [3, 4]. Это даёт возможность легко модернизировать существующий класс одноканальных бортовых РЛС и РЛС управления воздушным движением с целью повышения их эффективности для решения задач обнаружения и распознавания объектов. В данном случае модернизации подвергается СВЧ-тракт путём включения в него совмещенного преобразователя поляризации (СПП) сигнала. Такие РЛС относятся к классу одноканальных с модуляцией или манипуляцией сигнала на излучение и приём. Так в рамках работы [3] рассматривался алгоритм обработки радиолокационного сигнала, позволяющий производить оценку m и a при использовании сигналов с фиксированными круговыми поляризациями. Принцип работы такой РЛС заключается в излучении сигнала с круговой поляризацией, приёме отраженного сигнала на эту же антенну, разделении сигнала на ортогонально поляризованные круговые компоненты и нахождении отношения этих компонент в следующем виде [3] Когда отсутствуют фоновые отражения и собственные числа МР цели являютсядействительными величинами, то в этом случае на выходе амплитудного канала устройства деления получаем оценку степени анизотропии цели в виде [3] а на выходе измерителя разности фаз несущих ортогональных компонент сигнала имеем оценку (a *) угла ориентации собственного базиса цели относительно измерительного. При наличии фоновых отражений собственные числа МР (фон + объект локации) будут комплексными величинами и функциями времени. В этом случае получаем оценки m * и a * совокупной цели в виде - фон + объект локации. Эти параметры являются случайными функциями времени и условий радиолокационного наблюдения, поэтому необходимо исследовать эффективность их практического применения для задач обнаружения и распознавания объектов.Задачей исследований является построение вероятностной модели радиолока- ционного канала, позволяющего формировать параметры m и a , и получение качественных оценок эффективности их использования.
Обоснование выбора базовой вероятностной модели радиолокационного сигнала
.Используя результаты исследований [1, 2, 3] можно легко найти связь между (1) параметрами m и a и параметрами поляризационного отношения эллиптически поляризованной волны в линейно-ортогональном базисе, связанном с поляризационным разделителем, в случае излучения сигналов с круговой поляризацией
Такое положение справедливо только при локации стабильной цели, которая имеет действительные собственные числа МР, и отсутствии фона. В реальной обстановке рассеянный сигнал представляет собой сумму детерминированной и флюктуирующей составляющих, причём первая обусловлена наличием стабильного радиолокационного объекта наблюдения. Флюктуирующая составляющая сигнала определяется
наличием фона, который можно представить в виде большого числа независимых элементарных отражателей. Отраженный сигнал является в общем случае суммой сигналов, соответствующих элементарным отражателям и объектам, находящимся в пределах разрешаемого элемента зондируемого пространства ПРЛС. Изменение фазы и амплитуды элементарных сигналов, определяемых флюктуациями взаимного положения отражателей, приводит к амплитудным и фазовым флюктуациям результирующего отраженного сигнала. Если объекты локации малоразмерные, то интенсивность отражений от фона подстилающей поверхности может быть соизмерима и даже превышать мощность сигналов, отраженных от объектов локации. Поэтому обнаружение малоразмерных объектов представляется наиболее сложной и актуальной задачей при наблюдении реальных подстилающих сред.Поскольку обнаружение стабильного объекта производится на фоне мешающих отражений, то оценка степени анизотропии будет случайной функцией времени, определяемой огибающими и фазами ортогонально поляризованных компонент волны. При этом возникает необходимость использования статистической модели радиолокационного сигнала, за основу которой может принята модель, рассмотренная в работах
[1, 2]. Данная вероятностная модель была получена для квадратурных составляющих радиолокационного сигнала в раскрыве антенны, которые можно представить в следующем видеПри фиксированной поляризации излучения свойства квадратур полностью определяются статистической МР [1]
где первая матрица определяет свойства стабильного радиолокационного объекта, а вторая - свойства флюктуирующего фона. Если поляризация облучающей волны задана вектором Джонса
то общая форма записи мгновенного вектора электрического поля отраженного от объекта в произвольном базисе аналогична выражению (4)
Выражение для квадратур xm флюктуирующей части, а также анализ их свойств, приведены в работе [2]. Величины значений Zm можно получить при известной поляризации облучающей волны и значениях стабильных слагаемых Smnц в элементах матрицы (4). Используя известное правило функционального преобразования [5], можно совершить переход от совместной плотности вероятности квадратурных составляющих (3) к совместной плотности вероятности огибающих и разности фаз ортогонально-поляризованных компонент волны
В выражениях (8) и (9) использованы следующие обозначения:
![]() -
-
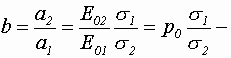
а
s 1 / s 2 – поляризационные свойства фоновой (флюктуирующей) составляющей рассеянного поля;d 0= ( j 02-j 01 ) - разность фаз между детерминированными ортогонально поляризованными составляющими сигнала;
![]()
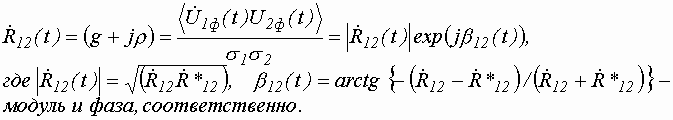
![]()
Согласно методике, подробно изложенной в работах [2, 5], найдена совместная плотность вероятности модуля и аргумента поляризационого коэффициента суммарной поляризованной волны для произвольного базиса
[e1, e2]: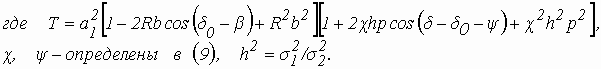
Построение вероятностной модели рассматриваемого РЛ канала.
Используя известное распределение плотности вероятности поляризационного коэффициента (11), полученное для произвольного базиса [e1, e2], проанализируем модель радиолокационного канала, выходными параметрами которого являются инвариантные и динамические параметры (m , a ) объектов локации на фоне помеховых отражений. Как было показано в [3, 4], радиолокационный канал подобного типа можно представить, используя формализм матриц Джонса, в следующем виде
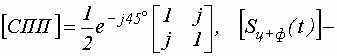
Подставляя оператор преобразователя поляризации в (13), найдем эквивалентную МР канала, предполагая при этом, что канал распространения сигнала туда и обратно не вносит никаких потерь и искажений
Очевидно, что при известной поляризации падающей волны, поляризация рас-сеянного сигнала полностью определяется свойствами объекта локации. Это утверждение справедливо и для поляризации сигнала, определяемого выражением (12), поскольку ортогонально поляризованные компоненты волны являются линейной комбинацией элементов МР.
Рассмотрим статистические характеристики поляризационных параметров
сигнала от цели (12) с учётом мешающих фоновых отражений от элемента разрешения ПРЛС.Пусть нам известны [1] статистические характеристики
(s 211, s 212, s 222) МР зондируемой местности, на которой находится объект. Будем также полагать, что детерминированная составляющая сигнала Еанал.(t) определяется стабильным радиолокационным объектом и описывается МР вида [3, 4]где
l 1, l 2 – собственные действительные числа МР стабильного объекта.Найдем параметры совместной плотности вероятности модуля и фазы поляризационного коэффициента, которые в случае разложения волны на линейные ортогональные компоненты в собственном базисе поляризационного разделителя (15) являются параметрами m * и a * объекта.
Детерминированные составляющие сигнала (15) определяются математическим ожиданием компонент Еx и Еyа флюктуирующие составляющие - дисперсией компонент сигнала
Тогда параметр a 2i ( i=1, 2) с учётом (17) и (18) определяется следующими соотношениями:
При этом обобщенный параметр суммарной волны b = a2 /a1
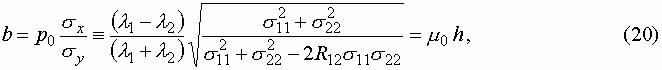
где m
0 - определяет степень анизотропии стабильного объекта, h = s x /s y - учитывает флюктуации m (t) за счёт мешающего действия помехи. Разность фаз между детерминированными составляющими сигнала, с учётом выражения (1), будет определять параметр a для стабильного радиолокационного объекта С учётом введённых обозначений перепишем совместную плотность вероятности для р и d, определяемую выражением (11)В качестве примера рассмотрим числовые характеристики и характер изменения вида совместной плотности вероятности инвариантного и динамического параметров m* и a* объекта локации для некоторых частных случаев. Так характер изменения совместной плотности вероятности W(m , a ) в зависимости от величины параметров a1, b, R, h при b = 0, a = 0 иллюстрируют рис. 1 и 2.
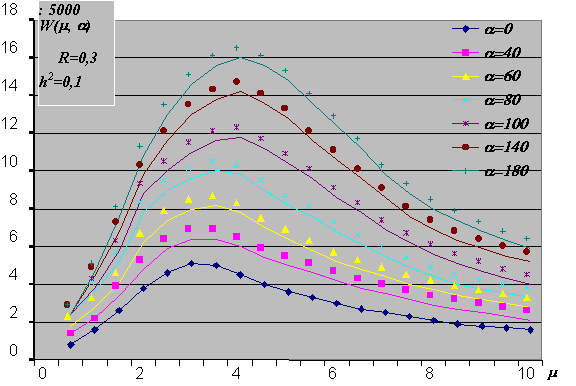
Совместная плотность вероятности поляризационных параметров m и a при различных параметрах a и фиксированных параметрах R, h и a=0 (i=1,2)
Рис. 1.
Вероятностная модель РЛ канала формирующего параметр m
.Одномерная плотность вероятности параметра m может быть найдена в результате функционального преобразования W(m , a ) следующим образом [5]
Используя данные работы [2] и результаты анализа, приведенные выше, получаем плотность вероятности
W(m)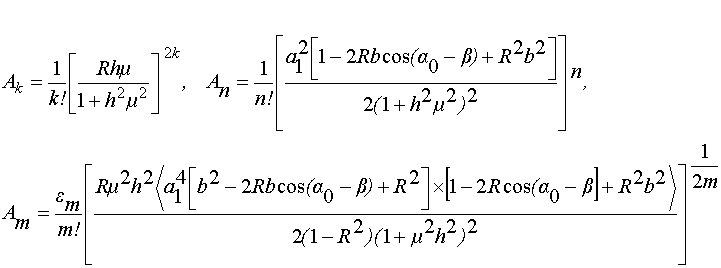
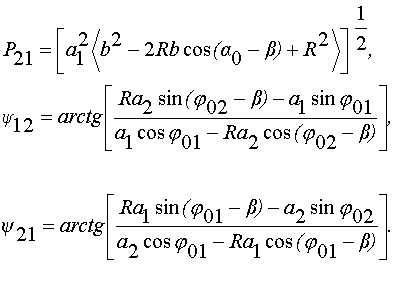
Графики плотности вероятности инвариантного параметра m обьекта локации представлены на рис. 3.
Из графиков видно, что при изменении параметров
a1, b, h вид плотности вероятности W(m ; a1, b, R, b , D m ) существенно изменяется. В случае отсутствия детерминированных составляющих (т.е. при отсутствии стабильного объекта локации) выражение для плотности вероятности W(m ; a1, b, h, R,b ) (24) значительно упрощается и приобретает следующий видХарактер изменение вида плотности вероятности инвариантного параметра m (25) в зависимости от величины R и h иллюстрирует рис. 4.
Для определения начальных моментов преобразованной случайной величины используем выражение [5]
и для определения центральных моментов следующее
Среднее значение и дисперсию инвариантного параметра m , плотность вероятности которого выражается (25), можно представить с учётом (26, 27) в виде следующих выражений [2]
По формулам (28), (29) построены графики в зависимости от параметра
R для различных значений h и представлены на Рис.5.Анализ приведенных формул и представленных на Рис.
(1-5) графиков показывает следующее:Из изложенного следует, что дисперсия оценки степени анизотропии цели, определяемая как "поляризационное отношение" в рассмотренной выше методике определения инвариантного параметра, резко уменьшается в случае, если на фоне местности появляется стабильная цель. Это уменьшение, в основном, обусловленно значительной корреляцией ортогональных компонент суммарной волны, появляющейся при наличии в этой волне детерминированной составляющей, обусловленной наличием сигнала от цели.
Вероятностная модель РЛ канала формирующего параметр a
.Найдем теперь одномерную плотность вероятности
W(a ) динамического параметра. Для этого достаточно проинтегрировать выражение (22) по исключающей переменной m [5]. В результате интегрирования (22) получается громоздкое выражение плотности вероятности суммарной волны, которое трудно поддается анализу. В случае равенства нулю модуля и аргумента коэффициента взаимной корреляции выражение значительно упрощается и его можно использовать для выяснения зависимости W(a ) от параметров a1, b, a 0 и h [2]. Выражение плотности вероятности W(a ) динамического параметра a в зависимости от параметров a1, b, a 0 и h имеет следующий вид Зависимость плотности вероятности W(a ) от параметра R получим для случая отсутствия детерминированных составляющих в принимаемом сигнале. Выражение плотности вероятности W(a ) динамического параметра a в этом случае значительно упрощается На рис.6 приведены семейства графиков плотности вероятности W(a ) поляризационного параметра a , расчитанных по формуле (30).Рис.6
Плотность вероятности
W(a ) поляризационного параметра "угол ориентации - a" в зависимости от параметров a1, b, и a0 .Анализ выражения (30) и рис.6 показывает, что плотность W(a ) определяется тремя параметрами: a1, b, a 0 , и в отличие от плотности вероятности W(m ) не зависит от отношения дисперсий параметра h2. Плотность вероятности W(a ) является одномодальной функцией, при этом мода функции совпадает со значением a = p + a0 (при изменении a в пределах 0¸p ). При a0=0 функция W(a ) симметрична относительно p и с увеличением параметров a1, b группируются вокруг среднего значения. На границах интервала (0, 2p ) плотность вероятности меньше, чем 1/ 2p , и по мере роста параметров a1 и b стремится к нулю. При равенстве нулю параметров a1 и b плотность вероятности W(a ) становится равномерной. При больших значениях параметров a1 и b, как показано в работе [2], уже при a1, b> 2¸ 3 точная формула (30) для W(a ) может быть апроксимирована нормальным законом
Среднее значение параметра a при увеличении параметров a1, a2 (a 0 ¹ 0) стремится к значению a = p +a 0 . Дисперсия s 2a с увеличением параметров a1, a2 уменьшается. Анализ выражений (30) - (32) позволяет выявить зависимость функции W(a ) от основных параметров a1, b, a 0 и R, а следовательно, и от поляризационных свойств источника излучения (отражения, рассеяния) частично поляризованных волн.
При решении многих практических задач требуется знание статистических характеристик параметра a
, если динамический параметр a0 является случайным и может быть аппроксимирован нормальным законом распределения. В этом случае плотность вероятности параметра a может быть представлена в виде [2]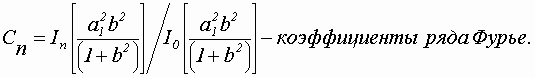
Для рассматриваемого случая среднее значение и дисперсия равны (2)
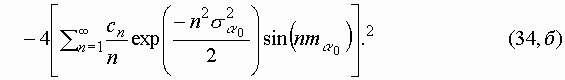
Заключение.
Результаты проведённых исследований эффективности использования таких параметров, как поляризационной степени анизотропии m и угла ориентации a собственного базиса цели относительно измерительного, для задач обнаружения, различения, распознавания образов и т.д. позволяют сделать следующие выводы.Результаты проведенных исследований автор предполагает использовать для изучения помехоустойчивости ПРЛС, использующих алгоритмы формирования поляризационных параметров m и a , и получения количественных оценок эффективности подавления пассивных помех. Наиболее эффективным показателем работы систем подавления являются её рабочие характеристики, которые могут быть получены на основе использования вероятностных моделей используемых параметров. В качестве таких рабочие характеристик будут использованы - коэффициент подавления помехи и коэффициент подпомеховой видимости.
Литература
Автор: С.П. Лукьянов, e-mail: Lukjanov.rff@elefot.tsu.ru