Трехпараметрическая модель фазовых переходов в ферромагнитном сплаве Ni-Mn-Ga

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5 , 2000
оглавление

дискуссия

ТРЕХПАРАМЕТРИЧЕСКАЯ МОДЕЛЬ ФАЗОВЫХ ПЕРЕХОДОВ
В ФЕРРОМАГНИТНОМ СПЛАВЕ Ni-Mn-Ga

В.Д. Бучельников^*, Д.Л. Далидович^**, А.Т. Заяк^*, В.Г. Шавров^**

^*Челябинский государственный университет^**Институт радиотехники и электроники РАН

Получена 15 мая 2000 г.

В рамках феноменологической теории фазовых переходов Ландау теоретически исследованы фазовые диаграммы структурных и магнитных фазовых переходов в ферромагнитном сплаве Ni-Mn-Ga с эффектом памяти формы при учете модуляционного параметра порядка. Показано, что в этом случае наравне с мартенситными превращениями могут иметь место так называемые предмартенситные и послемартенситные фазовые переходы, связанные с появлением модулированной структуры. Деформационный и модуляционный параметры порядка через взаимодействие с магнитным параметром порядка оказывают существенное влияние на магнитные фазовые переходы.

Введение

В последнее время структурные фазовые переходы являются объектами интенсивного исследования из-за их определяющей роли в таких эффектах, как сверхупругость и память формы. Особый интерес вызывают так называемые "мартенситные превращения" - структурные фазовые переходы первого рода из исходной высокосимметричной структуры в низкосимметричную искаженную структуру, существующую при низкой температуре [1]. При описании мартенситных превращений в рамках феноменологической теории Ландау главными параметрами порядка являются компоненты тензора деформаций. В этом случае мартенситные фазовые переходы могут быть описаны с помощью плотности свободной упругой энергии с учетом ангармонизма (собственный фазовый переход) [2]. Если мартенситные превращения происходят в ферромагнитной матрице, то благодаря существующему в ферромагнетиках магнитоупругому взаимодействию, они могут сопровождаться изменениями в магнитной подсистеме. В результате мартенситные превращения вызывают в ферромагнетике магнитные фазовые переходы.

Ферромагнитный сплав Гейслера Ni-Mn-Ga имеет кубическую структуру точечной группы симметрии O_h. В нем при понижении температуры происходит фазовый переход в тетрагональную структуру [3,4]. Мартенситные фазовые превращения и связанные с ними магнитные фазовые переходы в Ni-Mn-Ga в рамках теории Ландау подробно исследованы в работах [5-12].

В настоящее время надежно установлено, что мартенситные переходы могут сопровождаться появлением промежуточной модулированной фазы, характеризующейся набором волновых векторов q_i [13]. На эксперименте наличие промежуточной фазы проявляется в виде частичного смягчения соответствующих фононных мод [13,14]. Эксперименты показывают, что в Ni-Mn-Ga переход из исходной структуры в модулированную фазу является фазовым переходом 1-го рода [15], но с существенно меньшим скачком параметров порядка и теплоемкости, чем у самого мартенситного превращения. В работах [14,16] было показано, что структурный фазовый переход в модулированную фазу можно описывать в рамках теории Ландау с помощью свободной энергии, включающей в себя упругую энергию с учетом ангармонизма, членов, описывающих модулированную структуру, а также слагаемых, ответственных за взаимодействие тетрагональных деформаций с модуляционным параметром порядка. В этом случае тетрагональные деформации являются вторичными параметрами порядка, связанными с главными параметрами порядка, описывающими модулированную структуру. Деформации появляются одновременно с модуляцией в точке структурного перехода в модулированную фазу. Величина этих деформаций определяется величиной их коэффициента связи с модуляционным параметром порядка.

Среди большого количества твердых тел, в которых наблюдаются как мартенситные фазовые переходы без появления модулированной структуры, так и переходы с образованием промежуточной модулированной структуры, сплав Ni-Mn-Ga занимает особое место. Рентгеновские эксперименты показывают, что низкотемпературная мартенситная фаза этого сплава содержит как сильные тетрагональные искажения решетки (c/a~0.94), так и модуляцию тетрагональной структуры с вектором поляризации, параллельным оси , и волновым вектором, направленным вдоль оси [110] [17,18]. Первые исследования, проведенные в работе [17], обнаружили только одну точку (T=202 K) перехода в мартенситную фазу с модуляцией и тетрагональными искажениями. В более поздних экспериментах [19] были найдены две различные точки фазовых переходов. Первый переход, наблюдаемый при более высокой температуре, является переходом из симметричной кубической структуры в модулированную структуру с упомянутыми выше волновым вектором и вектором поляризации. Эта промежуточная фаза, названная в работе [19] "предмартенситной", имеет величину вектора модуляции, равную 1/3. Она представляет собой приблизительно кубическую структуру и сопровождается появлением малых тетрагональных деформаций. Второй фазовый переход - это переход из промежуточной модулированной структуры в действительно мартенситную фазу, имеющую большие тетрагональные искажения так же, как и модуляцию. Таким образом, необходимо обобщить феноменологический подход [2,5-12,14,16] так, чтобы он мог описывать два следующих друг за другом фазовых перехода.

Другая причина, по которой Ni-Mn-Ga привлекает большое внимание, состоит в том, что структурные фазовые переходы в нем происходят в ферромагнитной матрице. Оказывается, структурные изменения влияют не только на направление вектора намагниченности, но и на его модуль [5,9,11,12]. Имеются эксперименты, показывающие рост величины намагниченности при переходе в модулированную фазу [20]. Необходимо учесть и этот факт при феноменологическом описании.

Реальная магнитная структура деформированной фазы в Ni-Mn-Ga до сих пор в полной мере экспериментально не исследована. Известно только из измерений магнитной восприимчивости, что структурный переход в тетрагональную фазу сопровождается появлением сильной магнитной анизотропии [4]. В [21] построена феноменологическая модель неоднородной мартенситной структуры, которая появляется в сплаве Ni₂MnGa ниже температуры мартенситного перехода, и получены выражения для оценки статической магнитной восприимчивости и намагниченности мартенсита.

Недавно появилась теоретическая работа [22], посвященная моделированию предмартенситного фазового перехода в Ni₂MnGa методом Монте-Карло. Авторы [22] делают вывод о том, что предмартенситные эффекты являются результатом магнитоупругой связи между магнитной подсистемой и фононной модой, испытывающей смягчение при образовании модуляционного упорядочения. Предмартенситный переход происходит в том случае, когда данное магнитоупругое взаимодействие достаточно велико. Этот результат, говорит о том, что при построении феноменологической теории следует учитывать указанное взаимодействие. Полученная в [22] предмартенситная фаза не содержит тетрагональных деформаций. Тетрагональные деформации действительно не наблюдались в предмартенситной фазе [13], но это может быть связано с их очень малой величиной. Поэтому теоретическое рассмотрение тетрагональных деформаций, вызванных модуляционным упорядочением, становится необходимым. Эффекты, возникающие, например, в магнитной подсистеме, сопутствующие этим малым тетрагональным искажениям в предмартенситной фазе, позволили бы выявить наличие самих деформаций, если они имеют место.

В настоящей работе предложена феноменологическая теория фазовых переходов Ландау в кубическом ферромагнетике Ni-Mn-Ga, наиболее полно учитывающая все виды взаимодействий между параметрами порядка (магнитным, деформационным и модуляционным). Анализируется влияние данных взаимодействий на фазовую диаграмму. Показано, что в Ni-Mn-Ga наравне с мартенситными превращениями могут иметь место так называемые предмартенситные и послемартенситные фазовые переходы, связанные с появлением модулированной структуры. Деформационный и модуляционный параметры порядка через взаимодействие с магнитным параметром порядка вызывают в ферромагнетике магнитные фазовые переходы. Последний факт приводит к существенному разнообразию возможных магнитных состояний в кристалле.

Теория Ландау

В этой части статьи представлена теория Ландау для структурных фазовых переходов в кубическом кристалле, в котором при низкой температуре может осуществляться как модулированное, так и тетрагональное состояние, имеющее значительные тетрагональные искажения. Искажения кубической решетки при структурных переходах описываются однородными деформациями, записанными в виде линейных комбинаций компонент тензора деформаций e_ii (i=1,2,3) [2]

. (1)

Деформация e₁, соответствующая изменению объема, не нарушает симметрию решетки. Нарушение симметрии имеет место благодаря деформациям e₂ и e₃, ответственным за переход решетки из кубической фазы в тетрагональную. Данный переход сопровождается смягчением упругого модуля C₁₁-C₁₂. Полное выражение для плотности свободной энергии должно также содержать деформации e₄=e_xy, e₅=e_yz, e₆=e_zx, которые приводят к искажению элементарной ячейки до более низкой симметрии, чем тетрагональная.

Для описания в кристалле акустических фононных мод типа (1/3,1/3,0), необходимо отметить, что существует шесть различных направлений волнового вектора модуляции. Они могут быть записаны как: k₁=V (1,1,0), k₂=V (0,1,1), k₃=V (1,0,1), k₄=V (1,,0), k₅=V (0,1,) и k₆=V (,1,0), где V =1/3. В связи с этим, как правило, должен существовать параметр порядка, который содержит двенадцать компонент (шесть амплитуд и шесть фаз): y ₁ … y _6, j ₁ … j _6, где y _j=|y _j|exp(ij _j). Смещения атомов, соответствующие каждому из этих параметров порядка, имеют вид u_j(r)=|y _j|p_jsin(k_jr+j _j), где p₁,…,p₆ - единичные векторы поляризации, направленные соответственно вдоль осей [,1,0], [0,,1], [1,0,], [1,1,0], [0,1,1], [1,0,1]. Полное выражение плотности свободной энергии должно быть инвариантно по отношению к пространственным преобразованиям точечной группы симметрии O_h. Оно состоит из слагаемых трех типов:

F = F_e(e_j) + F_ψ(ψ_i) + F_eψ(e_j ,ψ_i ). (2)

Здесь F_e(e_j) - плотность упругой энергии, содержащая члены, ответственные за ангармонизм упругой подсистемы по отношению к параметру порядка (e₂, e₃). Ее выражение имеет вид [2]

(3)

где коэффициенты a, b, c являются линейными комбинациями компонент модулей упругости 2-го, 3-го и 4-го порядков соответственно

(4)

Поскольку выражение (3) содержит слагаемые третьего порядка, то фазовый переход по параметру порядка (e₂, e₃) является переходом 1-го рода. При подходе к точке структурного перехода в тетрагональную фазу упругий модуль a=C₁₁-C₁₂ стремится к нулю, и вблизи точки перехода (T ® T_M) его можно записать в виде a=a₀(T-T_M), где T_M - температура мартенситного перехода.

Полное выражение для Fy (y _i) приведено и детально разобрано в приложениях работ [16,23]. В работе [23] приведено более сложное выражение. В этой статье рассмотрим наиболее простой вариант модуляции. Будем учитывать только одну фононную моду 1/3(1,1,0), описываемую параметром порядка y =|y |exp(ij ) (индекс опущен для простоты записи), и использовать следующее сокращенное выражение для плотности модуляционной части свободной энергии:

(5)

Член этого выражения, с коэффициентом C₁, минимизируется по отношению к фазе:
(y ⁶+(y ^*)⁶) = |y |⁶(exp(-i6j )+exp(i6j )) = 2|y |²cos(6j ). Минимум энергии (5) реализуется при j =± p /6, ± p /2, ± 5p /6, если C₁>0, и j =0, ± p /3, ± 2p /3, p , если C₁<0. С учетом минимизации по фазе φ, находим, что все полученные ниже результаты от нее не зависят. В выражении (5) переобозначим C'=C₀-|C₁| и для устойчивости положим, что C'>0. Параметр A зависит от температуры и вблизи температуры перехода в модулированное состояние (T® Ty ) может быть представлен в виде A=A₀(T-Ty ).

Часть плотности свободной энергии F_ey, которая связывает деформации e_i с параметром порядка, описывающим модуляцию, должна иметь форму, инвариантную относительно всех операций симметрии, связанных с e_i и y _j. С учетом всех требований эта форма имеет вид

(6)

где - линейные комбинации квадратов амплитуд модуляционного параметра порядка |y |²:

(7)

Каждая имеет такие же симметрийные свойства по отношению к преобразованиям точечной группы симметрии O_h, как и соответствующие e_i. Выражение (6) отличается от плотности свободной энергии взаимодействия деформационного и модуляционного параметров порядка, приведенной в работе [16]. Во-первых, (6) не содержит фазу j , и, таким образом, деформации от нее не зависят. Во-вторых, (6) содержит меньшую степень |y _i|, как более важную для описания в рамках теории Ландау. Упрощенная форма энергии взаимодействия деформационного и модуляционного параметров порядка (при учете только фононной моды 1/3(1,1,0)) имеет вид

(8)

Объединение выражений (3), (5) и (6) дает искомое выражение для плотности свободной энергии в простейшем виде, которое позволяет описать фазовые переходы из высокосимметричной фазы в модулированную и низкотемпературную мартенситную фазу с большими тетрагональными искажениями.

Влияние ферромагнетизма на структурные фазовые переходы

Как уже упоминалось выше, сплав Ni-Mn-Ga занимает особое положение, поскольку структурные превращения в этом сплаве происходят в ферромагнитной матрице. Если в ранних работах по исследованию данного сплава делался акцент на то, что его точка Кюри существенно выше точек структурных переходов [6-8], то в работе [12] экспериментально и теоретически показано, что вариации в составе сплава могут приводить к сближению температуры Кюри и температур структурных переходов, в результате чего роль магнитоупругого взаимодействия резко возрастает. Так как в данной статье речь идет именно о Ni-Mn-Ga, то необходимо учесть в модели влияние магнитной подсистемы на структурные превращения. Как известно из эксперимента, магнитный момент сплава Ni-Mn-Ga определяется главным образом атомами марганца как в кубической, так и в деформированной фазе [17]. Таким образом, можно использовать простой способ описания ферромагнетика Ni-Mn-Ga с помощью одноподрешеточной магнитной подсистемы с вектором макроскопической намагниченности M. Свободная энергия должна также содержать члены, которые связывают компоненты намагниченности M с другими параметрами порядка системы. Для удобства описания введем в рассмотрение безразмерный вектор намагниченности m=M/M₀, где M₀ - намагниченность насыщения.

Вклад членов плотности свободной энергии, содержащих m_i, состоит из четырех частей. Первая из них связывает деформации e_i с компонентами намагниченности m_i и имеет вид

(9)

Это выражение представляет собой простейшую форму магнитоупругой энергии с феноменологическими магнитоупругими постоянными B₁, B₂ и B₃, которые считаются не зависящими от температуры. Вторая часть - это энергия магнитной анизотропии, которая описывает влияние абсолютно недеформированной кубической решетки на магнитную систему. Ее можно записать в виде

(10)

Здесь K₁ - это первая константа кубической анизотропии. Она также считается не зависящей от температуры. Третья часть описывает взаимодействие компонент вектора намагниченности m_i с модуляционным параметром порядка y _i. Инвариантная форма этого выражения, содержащая только низшие степени разложения по y _i и m_i, строится по аналогии с выражением (9), и имеет вид

(11)

где определяются формулами (7). Выражению для плотности свободной энергии (11) соответствует эффективная магнитная анизотропия, которая появляется при ненулевых |y_i|, т.е. только в модулированной фазе. Как и ранее, будем использовать только часть энергии (11), связанную с |y₁|² (индекс далее опускаем),

(12)

Постоянные N₁, N₂, N₃ также считаются не зависящими от температуры. Конкретные значения констант N_i будут подбираться путем сопоставления результатов теоретического анализа с экспериментальными данными. Наконец, четвертая часть плотности свободной энергии имеет обменное происхождение. Ее необходимо записать, чтобы учесть зависимость модуля вектора намагниченности m от температуры. В самом простом виде она имеет форму

(13)

Здесь a и d ₁ - обменные постоянные. Параметр обменного взаимодействия зависит от температуры и вблизи точки Кюри может быть представлен как a =a₀(T-T_c), где T_c - температура Кюри.

В итоге получаем выражение для плотности свободной энергии, состоящее из семи слагаемых

(14)

Это выражение описывает три фазовых перехода: точку Кюри, переход в модулированное состояние и переход в тетрагональную фазу.

Применение модели

Полное выражение для плотности свободной энергии системы (14) содержит переменные не ответственные за фазовые переходы, т.е. являющиеся косвенными параметрами порядка: e₁, e₄, e₅, e₆. После минимизации энергии по этим переменным происходит перенормировка ряда констант, входящих в (14): 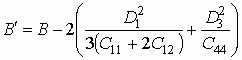, , 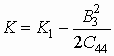, , 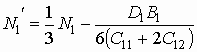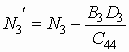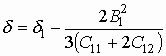. Выражение для плотности свободной энергии принимает вид

(15)

Для того, чтобы найти все равновесные состояния в рамках нашей модели, необходимо проминимизировать выражение (15) по всем оставшимся параметрам порядка: e₂, e₃, |y |, m₁, m₂, m₃. Анализ получающейся системы нелинейных алгебраических уравнений показывает, что ее точное аналитическое решение невозможно. Поэтому имеет смысл обращение к подходу, основанному на применении численных методов. Для упрощения расчетов там, где это возможно, следует перейти к безразмерным переменным. Проведем следующее переопределение параметров:

, , , , ,

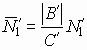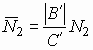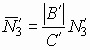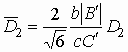, , , . (16)

Обозначив и 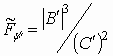, получаем соответствующие изменения во всех членах свободной энергии, содержащих e₂, e₃ и |y |. Параметр выбирается отрицательным, поскольку в данной модели переход в модулированную структуру является переходом 1-го рода. Ниже переобозначенные постоянные приводятся без черточек над ними. Обновленное выражение для плотности энергии имеет вид:

(17)

Проведенное преобразование позволило исключить из выражения для энергии постоянные c, b, C' и B'. Они продолжают косвенно входить в энергию через величины и , которые имеют размерность энергии. Количественное соотношение между и определено из сравнения расчетных скачков теплоемкости при переходах в модулированную и мартенситную структуры с экспериментальной зависимостью теплоемкости из работы [15]. Сравнение приводит к следующим значениям этих величин: » 1× 10¹⁰ эрг/см³, а » 1× 10⁶ эрг/см³. В работе [11] были проведены оценки многих параметров для Ni-Mn-Ga, в том числе и параметров b и c. Согласно этим оценкам b=1× 10¹² эрг/см³ и c=1× 10¹³ эрг/см³. Величина постоянной кубической анизотропии взята, как для Ni-содержащего ферромагнетика, K=-1× 10⁵ эрг/см³ [21]. Постоянная обменной магнитострикции принята, как в работе [11], B₂=1× 10⁷ эрг/см³. Намагниченность насыщения M₀=630 Э взята из работы [21]. Параметры, входящие в выражение для обменной энергии, приняты, исходя из анализа результатов работы [11]. На фазовой диаграмме из [11], построенной в координатах (a,a ), следует, что a =-1× 10⁹ эрг/см³ соответствует случаю, когда мартенситное превращение происходит из исходной кубической ферромагнитной фазы в тетрагональную симметричную фазу без промежуточной угловой тетрагональной фазы. Второй обменный параметр d подобран так, чтобы учесть близость к точке Кюри: d =5×10⁹ эрг/см³. Данные значения параметров должны соответствовать случаю, когда сплав находится в ферромагнитном состоянии, немного ниже точки Кюри (на 10-20 K). Эта ситуация отвечает нестехиометрическому составу сплава Ni-Mn-Ga [11].

Особую группу составляют параметры D₂, N₁`, N₂, N₃`, которые отвечают за взаимодействие модуляционного параметра порядка с другими параметрами. В литературе отсутствуют конкретные данные для их оценки. Вклад энергии F_eyнельзя определить из тех же соображений, что и и . Учет этого слагаемого означает, что появление модулированной структуры обязательно сопровождается малым тетрагональным искажением кристалла. Этот факт можно считать предположением модели, поскольку на эксперименте малые тетрагональные искажения такого типа не наблюдались. В частности, их безуспешно пытались обнаружить авторы работы [13]. Возможно эти деформации не наблюдаются именно из-за их малости. В теоретической работе [22] модель построена таким образом, что предмартенситная модулированная фаза не имеет тетрагональных искажений, что соответствует в нашей модели случаю D₂=0. Поэтому для получения более общего результата полагаем, что модуляция может сопровождаться появлением тетрагональных искажений, а их отсутствие является частным случаем.

Слагаемое, содержащее N₁`, является первым членом разложения обменной энергии по степеням параметра |y |. Будем считать, что наблюдаемое в [20] увеличение модуля намагниченности на ее температурной зависимости в предмартенситной фазе целиком обусловлено вкладом слагаемого с N₁`. Эта зависимость показывает, что вклад данного члена составляет » 1% от обменной энергии. Поэтому принимаем N₁`=-1× 10⁵ эрг/см³. Знак постоянной N₁` выбран отрицательным. Перенормированная обменная постоянная может быть записана в виде a `=(1/2)a +N₁`|y |². В [20] показано, что намагниченность в предмартенситной фазе увеличивается, а это возможно только в случае N₁`<0. Слагаемое в энергии с коэффициентом N₂ аналогично энергии магнитострикции. В зависимости от знака N₂ становится выгодным либо состояние с намагниченностью вдоль оси [001] (при N₂<0), либо состояние с M//[110] (при N₂>0). Параметр N₃` в выражении энергии также определяет магнитные состояния. При N₃`<0 выгодны состояния, в которых вектор намагниченности имеет компоненты m_x и m_y одного знака. Соответственно при N₃`>0 выгодны состояния с разнознаковыми m_x и m_y. Величины параметров N₂ и N₃` выбраны так, чтобы вклад от энергии был сопоставим с вкладом энергии F_ey: |N₂|=|N₃`| = 1× 10³ эрг/см³.

Для нахождения всех возможных состояний Ni-Mn-Ga, описываемых выражением для энергии (17), используется метод минимизации. Программа поиска минимума состоит из двух этапов. На первом этапе осуществляется нахождение начальных приближений всех возможных состояний вещества. На втором - находятся уточненные решения состояний одним из стандартных методов многомерного спуска [24]. Нахождение начальных приближений в задачах подобного типа является наиболее сложной проблемой. В данном случае для этого был использован подход, основанный на простом и эффективном методе генерации направлений в кристаллической решетке, предложенный в [25]. Этот подход удобен тем, что в сам метод генерации направлений заложена симметрия решетки. Метод дает равномерное распределение узлов сетки и является очень быстрым, т.к. не использует медленные функции, такие, как sin или cos. На этапе построения сетки все решения уже распределены по строго определенным областям, которые между собой не перекрываются. Это исключает возможность потери решения, что является слабым местом всех методов минимизации. На этапе уточнения решений остается методом многомерного спуска добиться требуемой точности и затем отобрать устойчивые решения. В качестве условия проверки на устойчивость использовано требование неотрицательности всех собственных значений. Фазовые диаграммы построены методом простого сканирования плоскости в заданных параметрах.

Рис. 1. Фазовая диаграмма сплава Ni-Mn-Ga в координатах a-A при b>0, D₂>0, N₁`, N₂, N₃`<0. Сплошные линии – линии фазовых переходов 1-го рода, штрих-пунктирная линия – линия фазового перехода 2-го рода, пунктирные линии – границы устойчивости фаз. F – ферромагнитная фаза, M – фаза с модуляцией, C – фаза с кубической решеткой, T – фаза с тетрагональной решеткой, ss’ и rr’ – термодинамические пути. В квадратных скобках показано направление вектора намагниченности в фазах.

На рис. 1 показана фазовая диаграмма Ni-Mn-Ga в координатах a и A при b>0, D₂>0, N₁<0, N₂<0, N₃<0. Сплошными линиями показаны линии фазовых переходов 1-го рода, пунктирными - границы областей устойчивости фаз, штрих-пунктирная линия отвечает линии фазового перехода 2-го рода. Из диаграммы видно, что в данном случае вещество может находиться в одном из пяти состояний. Буква F означает, что состояние является магнитоупорядоченным; C показывает, что структура решетки является кубической (аустенит); M показывает наличие модуляции; T означает структуру с большими тетрагональными искажениями (мартенсит). Индексы в обозначениях фаз показывают направление вектора намагниченности в фазах. На фазовой диаграмме линия OC является линией структурного и магнитного ориентационного фазовых переходов 1-го рода из высокотемпературной кубической (аустенитной) фазы FC_[111] в низкотемпературную (мартенситную) фазу FT_[001], которая имеет сильные тетрагональные искажения и не имеет модуляции. Фаза FC_[111] устойчива выше линии GH, а фаза FT_[001] - ниже линии MI. По зоне их перекрытия можно видеть, что этот переход сопровождается большим гистерезисом. Следует также отметить, что он идентичен мартенситному переходу между подобными фазами в работе [11]. На линии OB происходят структурный и магнитный ориентационный фазовые переходы 1-го рода из симметричной фазы FC_[111] в модулированную угловую фазу FCM_[uuw]. Исходная кубическая фаза устойчива правее линии JG, а модулированная - левее линии QF. Заметим, что фаза FCM_[uuw] не является строго кубической. В ней имеются малые тетрагональные искажения, которые появляются вместе с модуляцией. Величину тетрагональных деформаций определяет в данной фазе параметр D₂. Если принять D₂=0, то тетрагональных деформаций не будет, как это имеет место в промежуточной модулированной фазе, полученной в работе [22]. Экспериментальные данные не подтверждают наличие тетрагональных деформаций в фазе FCM_[uuw], но и не говорят об обратном [19]. Как и в [19], будем называть фазу FCM_[uuw] предмартенситной, имеющей квазикубическую решетку. На линии RX происходит магнитный ориентационный фазовый переход 2-го рода из угловой фазы FCM_[uuw] в симметричную фазу FCM_[001]. Подобный фазовый переход (без учета модуляционного параметра порядка) был аналитически описан в работах[7,8,10] на диаграмме в координатах (a, b). Там его существование было связано с взаимодействием намагниченности с деформационным параметром порядка (магнитоупругое взаимодействие). В данном случае указанный фазовый переход обусловлен взаимодействием модуляционного параметра порядка с деформационным (слагаемое в (17), пропорциональное постоянной D₂) или магнитным (слагаемое в (17), пропорциональное постоянной N₂) параметрами порядка. Существование рассматриваемого фазового перехода зависит от величины указанных взаимодействий и, следовательно, от величины малых тетрагональных искажений в квазикубических фазах. Линия RO является линией мартенситного и одновременно магнитного ориентационного фазовых переходов 1-го рода из угловой квазикубической фазы FCM_[uuw] в симметричную тетрагональную фазу FTM_[001], имеющую большие тетрагональные искажения. Существование данного фазового перехода также определяется взаимодействием модуляционного параметра порядка с деформационным или магнитным параметрами порядка. Он не имеет аналога на фазовой диаграмме в координатах (a, b) в [7,8,10], полученной без учета модуляционного параметра порядка. На линии RD имеет место мартенситный фазовый переход из симметричной квазикубичеcкой модулированной фазы FСM_[001] в тетрагональную симметричную модулированную фазу FTM_[001],, который сопровождается большим скачком тетрагональных деформаций. На этой линии не происходит переориентации вектора намагниченности и, следовательно, магнитного фазового перехода.

Анализ уравнений, описывающих минимум энергии (17), показывает, что положение точки R на линии OD, фазы FCM_[001] и линии ориентационного фазового перехода 2-го рода RX на фазовой диаграмме сильно зависят от величины параметров D₂ иN₂. Поскольку мы рассматриваем случай D₂ >>N₂, то их положение на фазовой диаграмме в основном определяется взаимодействием модуляционного и деформационного параметров порядка. Оказывается, что в зависимости от величины данного взаимодействия (а значит и от величины тетрагональных искажений, которые определяются этим взаимодействием в модулированных фазах), фаза FCM_[001] может либо присутствовать на фазовой диаграмме, либо нет.

Соответственно мартенситный переход на линии RD может либо сопровождаться магнитным ориентационным фазовым переходом, либо нет. На рис.1 представлена ситуация, когда параметр D₂ больше некоторой критической величины, при которой еще существует фаза FCM_[001]. Если параметр D₂ меньше этого критического значения, то фаза FCM_[001] и переход на линии RX на фазовой диаграмме отсутствуют, поскольку тетрагональные искажения в предмартенситной фазе не достигают необходимой величины. В этом случае на линии OD имеет место мартенситный фазовый переход 1-го рода из угловой квазикубической фазы FCM_[uuw] в симметричную тетрагональную фазу FTM_[001], имеющую большие тетрагональные искажения. Этот фазовый переход сопровождается магнитным ориентационным фазовым переходом 1-го рода, при котором происходит переориентация намагниченности от направления [uuw] на направление [001]. В зависимости от величины параметра D₂ линия QX меняет свое положение на диаграмме между линиями QL и QF. При увеличении D₂ происходит смещение линии QX в сторону линии QF (по часовой стрелке), но даже при очень больших значениях параметра D₂ они не совпадают, а имеет место асимптотическая сходимость. При уменьшении параметра D₂ ситуация другая. В этом случае линия QX приближается к линии QL (против часовой стрелки), а при некоторой величине параметра D₂ они сливаются. До их слияния на линии RX происходит ориентационный фазовый переход 2-го рода, а на линии RD – мартенситный переход, сопровождающийся скачками модуля намагниченности и тетрагональных деформаций, но не сопровождающийся переориентациенй намагниченности. При совпадении линий QX и QL мартенситный переход на линии OD сопровождается скачком ориентации и модуля намагниченности, а также тетрагональных деформаций одновременно. Таким образом, на линии OD в зависимости от параметров задачи происходит структурный фазовый переход 1-го рода либо из фазы FCM_[uuw], либо из фазы FCM_[001] в фазу FTM_[001]. Фаза FTM_[001] имеет как большие тетрагональные искажения, так и модуляционное упорядочение. На рис. 1 фаза FCM_[uuw] устойчива выше линии QX, фаза FCM_[001] – выше линии QL и ниже линии QX, а фаза FTM_[001] ниже линии KM.

Наконец, линия OE – это структурный фазовый переход 1-го рода между мартенситными тетрагональной фазой FT_[001] и модулированной тетрагональной фазой FTM_[001]. Данный переход не сопровождается магнитным фазовым переходом. Фаза FT_[001] устойчива правее линии NM, а фаза FTM_[001] устойчива левее линии PM. Следует отметить, что в фазе FT существуют равноценные по энергии состояния FT_[001], FT_[010], FT_[100] и т.д. Все эти решения, кроме FT_[001], которое связано с переходом в модулированное состояние FTM_[001], устойчивы правее линии MZ и становятся метастабильными на линии OE. Таким образом, в модулированной фазе снимается вырождение решений, связанное с кристаллической симметрией.

О том, как соотносятся тетрагональные деформации в предмартенситных фазах FCM_[uuw], FCM_[001] и в мартенситной фазе типа T, можно судить по рис. 2.

Рис. 2. Зависимость a) тетрагональных деформаций e₃, b) полярного угла вектора намагниченности q , c) модуляционного параметра порядка |y | и d) модуля вектора намагниченности M от величины модуля упругости второго порядка a на термодинамическом пути ss ’ (A) и rr ’ (B) (рис.1). На вставках показано изменение указанных величин в большем масштабе.

На рис. 2A показана эволюция параметров порядка на термодинамическом пути, соответствующем линии ss’ на рис. 1. Этот путь соответствует случаю понижения температуры. Из рис. 1 видно, что путь ss’ пересекает два фазовых перехода 1-го рода и один фазовый переход 2-го рода. По порядку следования первый из них - это структурный переход (сопровождающийся переориентацией намагниченности) из кубической решетки в модулированную, второй – это магнитный ориентационный переход, третий - отвечает мартенситному превращению без переориентации намагниченности. На рис. 2Aа показано изменение деформаций e₃, которое соответствует тетрагональному искажению решетки. На вставке приведен участок пути ss’ от его начала до точки мартенситного перехода, не включая последнюю. Здесь тетрагональные искажения обусловлены появлением модуляционных деформаций из-за взаимодействия магнитного и модуляционного параметров порядка. В масштабе тетрагональных деформаций в мартенситной фазе наличие слабых тетрагональных искажений в предмартенситной фазе незаметно из-за их малости. В связи с этим можно утверждать, что фаза типа CM является квазикубической. На рис. 2Ab представлено изменение полярного угла вектора намагниченности. Азимутальный угол j постоянен и равен p /4. Изменение полярного угла на рис. 2Ab показывает, как происходит переориентация вектора намагниченности в фазе FCM_[uuw] с направления [111] на направление [001]. На рис. 2Ac приведен модуляционный параметр |y |; на вставке показан его скачок при мартенситном переходе. Рис. 2Ad показывает изменение модуля намагниченности m=|M|/M₀ в монодоменном образце. Рост модуля намагниченности в предмартенситных фазах FCM_[uuw] и FCM_[001] обусловлен увеличением модуляционного параметра порядка |y | из-за перенормировки обменной постоянной слагаемым в энергии (17) при коэффициенте N₁: a `=(1/2)a +N₁`|y|².

Рассмотрим термодинамический путь rr’ на рис. 1. Он также соответствует понижению температуры, но при других условиях, нежели путь ss’. Эволюция параметров порядка в данном случае показана на рис. 2B. Следует отметить, что последовательность структурных переходов на пути rr’ иная, чем на пути ss’. При понижении температуры исходная фаза FC_[111] путем структурного перехода 1-го рода, сопровождающегося переориентацией намагниченности, превращается в немодулированную тетрагональную фазу FT_[001] (мартенситный переход), а она, в свою очередь, также посредством перехода 1-го рода без переориентации вектора намагниченности превращается в модулированную фазу FTM_[001]. Переход из фазы FT_[001] в фазу FTM_[001] сопровождается появлением модуляции (рис. 2Bс) с незначительным скачком величины тетрагональной деформации, который в масштабе рис. 2Bа не виден (он показан на вставке). Напомним, что в фазе FT существуют эквивалентные по энергии и симметрийным свойствам решения типа FT_[001], FT_[100] и FT_[010], чему отвечает верхняя часть кривой на рис. 2Bа. Появление модуляции в фазе FTM снимает вырождение решений и остается только одно из них - FTM_[001]. Модуляция также приводит к увеличению намагниченности (рис. 2Bd), но не изменяет ее ориентации. Данный переход можно назвать послемартенситным. Таким образом, можно сделать вывод о том, что предмартенситный переход имеет место только при определенных условиях (путь ss’). В других случаях модуляция может появляться в результате послемартенситного перехода (путь rr’). По-видимому, определяющее значение здесь может иметь концентрация сплава [11].

Если показанную на рис. 1 фазовую диаграмму построить при b<0 и D₂<0, то общая картина структурных и магнитных фазовых переходов не будет отличаться от рис. 1, однако с точки зрения направления намагниченности и типа тетрагональных деформаций фазы будут другими. В работах [7,8,10] было показано, что знак b определяет знак тетрагональных искажений. Так, в случае b>0 (рис. 1) деформация e₃<0. При b<0 деформация e₃ имеет противоположный знак. В соответствии с тетрагональными искажениями устанавливаются и равновесные магнитные состояния. В симметричных квазикубических модулированных и тетрагональных фазах при b>0 M параллельна оси типа [001], а при b<0 M параллельна оси типа [110]. В угловых квазикубических модулированных фазах намагниченность при b>0 вращается от оси [111] к оси [001], а при b<0 – к оси [110]. Соответствия между структурными и магнитными состояниями в Ni₂MnGa при b<0 и b>0 подробно разобраны в работах [7,8,10].

Характер взаимодействия модуляционного параметра порядка |y | и параметра тетрагональных искажений e₃ зависит от знака слагаемого в (8). В случае диаграммы на рис. 1 знаки деформаций e₃ и коэффициента D₂ таковы (b>0, D₂>0), что тетрагональные деформации в промежуточных фазах FCM_[uuw] и FCM_[001] того же типа, что и в низкотемпературной мартенситной фазе. Аналогично ведут себя деформации и при b<0, D₂<0. Но возможен другой вариант. Например, при b>0, D₂<0, N_2,3£ 0, слагаемое делает невыгодными тетрагональные деформации, которые должны быть в мартенситной фазе. Модуляция приводит к появлению в предмартенситной фазе тетрагональных искажений противоположного знака – тех, которые существовали бы при b<0. В этом случае имеет место ситуация, показанная на фазовой диаграмме на рис. 3.

Рис.3. Фазовая диаграмма сплава Ni-Mn-Ga в координатах a-A при b>0, D₂<0, N₁`, N₂, N₃`<0. Обозначение такие же, как и на рис. 1.

Видно, что в здесь имеется также 5 равновесных состояний того же типа, что и на рис. 1. Однако переориентация намагниченности в угловой модулированной фазе на линии RX происходит не на ось [001], а на ось [110]. Кроме того, на линиях мартенситного фазового перехода OR и RD всегда происходит и ориентационный фазовый переход 1-го рода.

Рассмотрим термодинамический путь ll` на рис. 3 и соответствующие ему изменения параметров порядка на рис. 4 для сравнения с их изменением на термодинамическом пути ss` (рис. 1).

Рис.4. Зависимость тех же величин, что и на рис.2, от модуля упругости a на термодинамическом пути ll` (рис.3). На вставках дан больший масштаб.

Если следовать по линии ll`, то сначала происходит структурный фазовый переход 1-го рода, сопровождающийся переориентацией вектора намагниченности, из исходной кубической фазой FC_[111] в квазикубическую модулированную фазу FCM_[uuw], в которой направление намагниченности изменяется сложным образом (рис. 4b). В фазе FCM_[uuw] сначала вектор намагниченности отклоняется от направления [111] к направлению [001], а затем - в обратном направлении, т.е. к оси [110]. Такое поведение вектора намагниченности связано с конкуренцией двух слагаемых в выражении энергии (17). Первое из них – обычная энергия магнитоупругого взаимодействия пропорциональная постоянной магнитострикции B₂, а второе – энергия взаимодействия модуляционного и магнитного параметров порядка пропорциональная постоянной N₂. Эти слагаемые можно записать в виде B₂^’ e₃ (3m_z²-m²), где B₂^’=B₂+6^1/2N₂|y |²/(3e₃). Из [8] известно, что знак коэффициента B₂^’ определяет направление вектора намагниченности в мартенситной тетрагональной фазе. При b>0 и B₂^’>0 в тетрагональной фазе намагниченность направлена вдоль оси [001], а при B₂^’<0 – вдоль оси [110]. Фаза FCM_[uuw] имеет малые тетрагональные искажения (рис. 4a) e₃>0, свойственные по знаку случаю b<0, но мы имеем b>0. Знак этих деформаций определяется в данном случае параметром D₂. Знак же коэффициента B₂^’ в фазе FCM_[uuw] определяется конкуренцией магнитоупругого взаимодействия и взаимодействия модуляционного и магнитного параметров порядка. Вначале на пути l l ` основной вклад в B₂^’ дает магнитоупругое взаимодействиие, поэтому B₂^’>0 и намагниченность в фазе FCM_[uuw] вращается к оси [001]. Затем становится преобладающим вклад от взаимодействия модуляционного и магнитного параметров порядка, знак B₂^’ изменяется на противоположный и намагниченность начинает переориентироваться на ось [110]. Далее при понижении температуры на линии RX происходит магнитный ориентационный фазовый переход 2-го рода, при котором намагниченность переходит из угловой фазы FCM_[uuw] в симметричное состояние FCM_[110]. Существование данного магнитного фазового перехода связано с взаимодействием деформационного и модуляционного параметров порядка. Затем на линии RD имеет место мартенситное превращение. При этом изменяется знак тетрагональных деформаций e₃ параметр B₂^’ снова становится положительным, что и приводит к переориентации вектора намагниченности с оси [110] на ось [001] при данном структурном переходе. Сравнение рис. 2A и рис. 4 показывает, что изменение знака параметра D₂ в значительной степени определяет характер предмартенситных фаз, а значит, и самого мартенситного превращения.

Рис.5. Фазовая диаграмма сплава Ni-Mn-Ga в координатах D₂ - ss’ (при изменении параметров a и A, соответствующим термодинамическому пути ss’) в случае b>0, N₁`, N₂, N₃`<0. При D₂ < 0 путь ss’ (рис. 1) трансформируется в путь ll’ (рис. 3).

На рис.5 приведена фазовая диаграмма в координатах D₂ - ss` (рис. 1) при b>0, N₂<0, N₃<0. Отметим, что на термодинамическом пути ss` переменные a и A связаны между собой линейной зависимостью. При D₂<0 путь ss` соответствует пути ll` на рис. 3. Здесь линия TL есть линия структурного и ориентационного фазовых переходов 1-го рода из кубической фазы FC_[111] в квазикубическую угловую модулированную фазу FCM_[uuw]. Линии GV и GN являются линиями ориентационных фазовых переходов 2-го рода из фазы FCM_[uuw] в квазикубические симметричные модулированные фазы FCM_[001] и FCM_[110] соответственно. Наконец, на линии XQ происходит мартенситное превращение. Этот переход либо сопровождается спиновой переориентацией (линия GQ), либо нет (линия GX).

По данной диаграмме можно проследить также влияние параметра N₂ на состояния ферромагнетика. При отрицательном N₂ точка G смещается вниз по координате D₂, т.е. отрицательный параметр N₂ способствует увеличению области существования фазы FCM_[001] с намагниченностью, направленной вдоль оси [001]. В случае N₂=0 реализуется ситуация, когда фазовая диаграмма в координатах D₂ - ss` (рис. 5) симметрична относительно горизонтальной оси, т.е. точка G лежит на оси ss`. При N₂>0 точка G смещается верх по оси координат D₂. В этом случае увеличивается область существования фазы FCM_[110] с намагниченностью вдоль оси [110]. Таким образом, в зависимости от знаков D₂ и N₂ на пути ss` могут развиваться различные сценарии фазовых превращений. Из рис. 5 следует, что изменение знака D₂ может не приводить к замене фазовой диаграммы, приведенной на рис. 1, к диаграмме, которая показана на рис. 3 и наоборот. Видно, что необходимо учитывать величину и знак параметра N₂, влияние которого на фазовую диаграмму может быть существенным. В предмартенситной фазе FCM_[uuw] при изменении D₂ (рис. 5) параметры порядка изменяются сложным образом. При переходе от линии GV к линии GN намагниченность вращается от оси [001] к оси [110]. При этом слабые тетрагональные деформации изменяют знак. Мартенситный переход на линии GQ из фазы FCM_[110] в фазу FTM_[001] сопровождается существенно более широким гистерезисом, чем выше точки G, где мартенситный переход имеет место на линии GX. Это связано с различными типами тетрагональных искажений в предмартенситных фазах. Следует отметить, что данная ситуация изменится, если поменять знак модуля упругости третьего порядка b. В этом случае изменяется знак тетрагональных деформаций в мартенситной фазе и направление намагниченности в ней соответственно с оси [001] на ось [110], что приводит к появлению большого гистерезиса выше точки G.

Помимо структурных и магнитных ориентационных фазовых переходов предложенная модель позволяет описать магнитный фазовый переход типа беспорядок-порядок (точка Кюри).

Рис. 6а

Рис. 6b.

Рис. 6с.

Рис.6. Фазовая диаграмма сплава Ni-Mn-Ga в координатах a -A при разных значениях величины модуля упругости второго порядка a>0 и при b>0, D₂>0, N₁`, N₂, N₃`<0. Сплошные линии – линии фазовых переходов 1-го рода, штрих-пунктирные линии – линии фазовых переходов 2-го рода, пунктирные линии – границы устойчивости фаз. P – парамагнитная фаза, F – ферромагнитная фаза, M – фаза с модуляцией, C – фаза с кубической решеткой. В квадратных скобках показано направление вектора намагниченности в фазах. Рис. 6а отвечает случаю, когда на диаграмме a -a без учета модуляционного параметра порядка (см. [5,9,11,12]) при изменении обменного параметра a имеет место фазовый переход 2-го рода из парамагнитной кубической фазы в ферромагнитную кубическую фазу, рис. 6b - случаю, когда сначала происходит фазовый переход 2-го рода из парамагнитной кубической фазы в ферромагнитную кубическую фазу, а затем мартенситный и ориентационный фазовые переходы 1-го рода из кубической ферромагнитной фазы в тетрагональную ферромагнитную фазу и, наконец, рис. 6с – случаю, когда фазовый переход из парамагнитной кубической фазы в тетрагональную ферромагнитную фазу является структурным и одновременно магнитным (типа беспорядок-порядок) фазовым переходом 1-го рода.

На рис. 6 приведена фазовая диаграмма в координатах a -A при разных значениях величины модуля упругости второго порядка a. Рис. 6а соответствует случаю, когда на диаграмме a -a без учета модуляционного параметра порядка (см. [5,9,11,12]) при изменении обменного параметра a имеет место фазовый переход 2-го рода из парамагнитной кубической фазы в ферромагнитную кубическую фазу, рис. 6b - случаю, когда сначала происходит фазовый переход 2-го рода из парамагнитной кубической фазы в ферромагнитную кубическую фазу, а затем мартенситный и ориентационный фазовые переходы 1-го рода из кубической ферромагнитной фазы в тетрагональную ферромагнитную фазу и, наконец, рис. 6с – случаю, когда фазовый переход из парамагнитной кубической фазы в тетрагональную ферромагнитную фазу является структурным и одновременно магнитным (типа беспорядок-порядок) фазовым переходом 1-го рода.

Рассмотрим фазовую диаграмму на рис. 6а. Видно, что при выбранном значении параметра a на диаграмме может осуществляться 7 равновесных состояний. Фаза PC является парамагнитной кубической фазой. На линии OB происходит структурный фазовый переход 1-го рода в модулированную квазикубическую парамагнитную фазу PCM, в которой появляются малые тетрагональные искажения за счет взаимодействия модуляционного и деформационного параметров порядка. Затем на линии ML имеет место мартенситный переход 1-го рода из фазы PCM в тетрагональную модулированную фазу PTM с большими тетрагональными деформациями. Линия OM является линией магнитного фазового перехода 2-го рода между модулированными квазикубическими парамагнитной (PCM) и ферромагнитной (FCM_[001]) фазами. На линии MQ происходит аналогичный переход между тетрагональными модулированными фазами PTM и FTM_[001]. Линия ON является линией ориентационного фазового перехода 2-го рода между квазикубическими модулированными симметричной (FCM_[001]) и угловой (FCM_[uuw]) фазами. На линиях MN и NP происходит мартенситный переход из этих фаз в тетрагональную ферромагнитную фазу FTM_[001]. Линия OD является линией структурного и ориентационного фазовых переходов из ферромагнитной кубической фазы FC_[111] в модулированную квазикубическую угловую фазу FCM_[uuw]. Наконец, на линии OC имеет место магнитный фазовый переход 2-го рода между парамагнитной PC и ферромагнитной FC кубическими фазами. Область устойчивости фазы PC ограничена линиями OC и OI, фазы FC – OC и OH, фазы PCM – OK, OQ и QR, фазы PTM – OF и OU, фазы FTM_[uuw] – OE, ES и OG, фазы FCM_[001] – OQ, QE и EO, фазы FTM_[001] – OF и OT.

Из диаграммы следует, что при выбранном значении параметра a фазовые переходы между парамагнитными и ферромагнитными фазами при всех значениях параметров a и A являются фазовыми переходами 2-го рода. Фазовая диаграмма, представленная на рис. 6b, отличается от рассмотренной выше тем, что здесь появляется магнитный фазовый переход 1-го рода между парамагнитной модулированной квазикубической фазой PCM и тетрагональной ферромагнитной фазой FTM_[001]. Этот переход происходит на линии XM и он сопровождается появлением больших тетрагональных искажений (мартенситный переход). На линии VX по-прежнему имеет место магнитный фазовый переход 2-го рода между мартенситными модулированными фазами PTM и FTM_[001]. Фаза PTM теперь устойчива в области выше линии VXWV’, а фаза FTM_[001] – ниже этой линии.

На фазовой диаграмме, приведенной на рис. 6c, остается лишь один магнитный фазовый переход 2-го рода – между фазами PTM и FTM_[001] на линии FR. Остальные переходы являются переходами 1-го рода. В отличие от рассмотренных выше случаев, здесь имеется всего 4 равновесных состояния – PC, FT_[001], PTM и FTM_[001]. Фаза PC устойчива в области правее линии IND, фаза FT_[001] – ниже линии VMH, фаза PTM – выше линии FMU, а фаза FTM_[001] – левее линии FMG. На линии RB происходит структурный переход между парамагнитной кубической фазой PC и парамагнитной модулированной квазикубической фазой PTM. Линия RO является линией магнитного и структурного фазового перехода между парамагнитной кубической фазой PC и мартенситной модулированной ферромагнитной фазой FTM_[001], а линия OD есть линия структурного фазового перехода между ферромагнитными фазами FT_[001] и FTM_[001]. Магнитный и мартенситный фазовые переходы между кубической парамагнитной фазой PC и тетрагональной ферромагнитной фазой FT_[001] происходит на линии OC.

Из сравнения фазовых диаграмм, приведенных на рис. 6, следует, что на первых двух диаграммах (рис. 6a и 6b) переход из кубической фазы в тетрагональную фазу всегда должен сопровождаться предмартенситным фазовым переходом. В третьем случае (рис. 6c) это переход либо вообще не сопровождается предмартенситными явлениями, либо он может сопровождаться лишь послемартенситным фазовым переходом.

Заключение

Построенная в данной работе феноменологическая теория фазовых переходов сплава Ni-Mn-Ga позволяет описать последовательное осуществление двух структурных переходов: из кубической решетки в модулированную фазу со слабыми тетрагональными искажениями (предмартенситный переход), а затем из модулированной квазикубической структуры в мартенситную с большими тетрагональными искажениями и модуляцией. Модель также позволяет описывать случай, когда сначала происходит фазовый переход из кубической фазы в немодулированную тетрагональную фазу (мартенсит), а затем из мартенситной фазы в модулированную мартенситную фазу (послемартенситный переход). Эти переходы могут сопровождаться магнитными фазовыми переходами. Получено, что модуляция решетки может иметь место и в парамагнитных фазах. Магнитный фазовый переход в точке Кюри может быть как 2-го, так и 1-го рода. Переход из парамагнитной фазы в тетрагональную фазу может происходить и без дополнительного перехода в модулированную квазикубическую фазу Показано, что взаимодействия между деформационным и модуляционным параметрами порядка, а также между модуляционным и магнитным параметрами порядка может существенно влиять на картину магнитных и структурных фазовых переходов сплава. Сделан вывод о том, что наличие в предмартенситной модулированной структуре малых тетрагональных искажений (не наблюдавшихся пока на эксперименте) может вызывать в этой фазе переориентацию вектора намагниченности и приводить к дополнительному магнитному ориентационному фазовому переходу 2-го рода. Проведен анализ влияния параметров феноменологического разложения на состояния, описываемые моделью. Особое внимание уделено параметрам, определяющим взаимодействие модуляционного упорядочения с другими параметрами порядка. Показано, что величина параметров этих взаимодействий оказывает существенное влияние на фазовую диаграмму сплава Ni-Mn-Ga. Это говорит о необходимости проведения дальнейших экспериментальных исследований с целью их определения.

Работа выполнена при поддержке грантов РФФИ 99-02-18247 и Минобразования 97-0-7.0-11.

Литература

1. Бойко В.С., Гарбер Р.И., Косевич А.М. Обратимая пластичность кристаллов. - М.: Наука, 1991.

2. Fradkin M.A. Phys. Rev. B, 1994, 50, p.16326-16339.

3. Васильев А. Н., Кокорин В. В., Савченко Ю. И. и др. ЖЭТФ, 1990, 98, с.1437-1440.

4. Vasil`ev A. N., Keiper A.R., Kokorin V.V. et al. Int. J. of Applied Electromagnetics in Materials, 1994, 5, p.163-169.

5. Божко А.Д., Бучельников В.Д., Васильев А.Н. и др. Письма в ЖЭТФ, 1998, 67, с.212-216.

6. Бучельников В.Д., Васильев А.Н., Дикштейн И.Е., Шавров В.Г. ФММ, 1998, 85, №.1, с.5-11.

7. Бучельников В.Д., Васильев А.Н., Дикштейн И.Е. и др. ФММ, 1998, 85, №.3, с.54-63.

8. Бучельников В.Д., Васильев А.Н., Заяк А.Т. и др. Вестник Челябинского университета, серия 6 "Физика", 1998, №1, с.20-32.

9. Бучельников В.Д., Васильев А.Н., Дикштейн И.Е. и др. Вестник Челябинского университета, серия 6 "Физика", 1998, №1, с.5-15.

10. Buchelnikov V.D., Romanov V.S., Zayak A.T. JMMM, 1999, 191/1-2, p.203-206.

11. Vasil`ev A.N, Bozhko A.D., Khovailo V.V. et al. Phys. Rev. B, 1999, 59, p.1113-1120

12. Божко А. Д., Васильев А.Н., Ховайло В.В. и др. ЖЭТФ, 1999, 115, с.1740-1755.

13. Zheludev A., Shapiro S.M., Wocher P. Phys. Rev. B, 1996, 54, p.15045-15050.

14. Krumhansl J.A., Gooding R.J. Phys. Rev. B, 1989, 39, p.3047-3056.

15. Planes A., Obrado E., Gonzales-Comas A. et al. Phys. Rev. Lett., 1997, 79, p.3926-3933.

16. Gooding R.J., Krumhansl J.A. Phys. Rev. B, 1988, 38, p.1695-1703.

17. Webster P.J., Ziebeck K.P.A., Town S.L. et al. Philos. Mag., 1984, 49, p.295-310.

18. Кокорин В.В., Мартынов В.В., Черненко В.А. ФТТ, 1991, 33, c.1250-1252.

19. Zheludev A., Shapiro S.M., Wochner P., et al. Phys. Rev. B, 1995, 51, p.11310-11314.

20. F. Zuo, X. Su, K.H. Wu. Phys. Rev. B, 1998, 58, p.11127-11130.

21. L`vov V.A., Gomonaj E.V., Chernenko V.A. J. Phys.: Condens. Matter, 1998, 10, p.4587-4596.

22. Castan T., Vives E., Lindgard P.-A. Phys. Rev. B, 1999, 60, p.7071-7084.

23. Folkins I.A., Walker M.B. Phys. Rev. B, 1989, 40, p.255-262.

24. Шуп Т. Решение инженерных задач на ЭВМ. - М.: Мир, 1982.

25. Шереметьев И.А., Изергин Д.Б., Игнатов Д.А. Вестник Челябинского университета, серия 6 "Физика", 1998, № 1, с.64-69.

Авторы:
Бучельников Василий Дмитриевич
Далидович Денис Леонидович
Заяк Алексей Тимурович
Шавров Владимир Григорьевич, e-mail: shavrov@mail.cplire.ru

оглавление

дискуссия