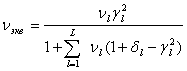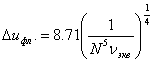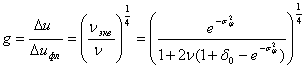"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 5, 2002

оглавление

дискуссия

 

Разрешающая способность адаптивных антенных решеток

при наличии флуктуаций параметров

 

Серебряков Г.В., e-mail: gserebryakov@mail.ru

 

Институт Прикладной Математики и Кибернетики, Нижний Новгород.

 

 

 

Получено 19.05.2003 г.

 

        Проанализирована потенциальная разрешающая способность адаптивных антенных решеток при наличии быстрых по сравнению со временем адаптации фазовых и амплитудных ошибок. Для простого случая двух внешних сигналов получены аналитические выражения предельного углового расстояния в зависимости от интенсивности ошибок и мощности входного сигнала.  

 

1. Введение

2. Модель сигнала

3. Быстрые фазовые и амплитудные ошибки

4. Разрешение источников излучения

5. Список литературы

 

 

1. Введение.

 

        Хорошо известно, что использование адаптивных антенных решеток для задач углового разрешения источников позволяет разрешать близко локализованные сигналы, если входное отношение сигнал-шум (ОСШ) достаточно велико [1-4]. В тоже время, применение адаптивных методов для задач локализации требует априорного знания геометрии антенной решетки и амплитудно-фазовых соотношений в приемных элементах. Фактически же благодаря различным причинам (это могут быть, например, деформации антенной решетки или искажения вносимые каналом распространения)  как местоположение сенсоров, так и амплитудно-фазовые характеристики приемных элементов могут существенно отличаться от номинальных. Более того, эти параметры могут быть флуктуирующими во времени, если параметры среды распространения флуктуируют. Влияние статических ошибок на характеристики  адаптивных методов  пространственного разрешения изучалось во многих работах (см., например, [5-8]). В настоящей работе аналитически и численно  изучается потенциальная разрешающая способность адаптивной антенной решетки при наличии быстрых по сравнению со временем адаптации амплитудных и фазовых флуктуаций. Мы будем полагать, что эти флуктуации являются стационарными и независимыми от элемента к элементу, с одинаковым статистическим распределением.  Конечно, ошибки, наблюдаемые при относительном движении приемных сенсоров в некоторых реальных приложениях (например, при использовании  буксировочных гидроакустических  антенн) должны считаться зависимыми в различных элементах и иметь различное статистическое распределение. Однако в настоящей работе мы рассматриваем подход к анализу проблемы лишь  в первом приближении.

 

 

2. Модель сигнала.

 

        Рассмотрим линейную эквидистантную антенную решетку из N равнонаправленных элементов. Предположим, что на антенну падают L (L < N) узкополосных некоррелированных между собой сигналов, размещенных в дальней зоне и представимых в виде плоских волн. Определим углы прихода этих сигналов по отношению к нормали антенны как  . Выходной сигнал с  k-ого приемного элемента может быть записан в виде

(1)                                           

где   означает сигнал излученный l-ым источником с мощностью , и  - пространственно некоррелированный стационарный белый шум с нулевым средним и интенсивностью   в каждом приемном элементе. Фазовый сдвиг  между элементами дается выражением  , где d - расстояние между элементами и l - длина волны узкополосных сигналов. Пространственная ковариационная матрица принимаемых  сигналов  при отсутствии ошибок запишется в виде

(2)                                          

где - пространственная ковариационная матрица l-ого сигнала,  – вектор размерности N , описывающий сигнал приходящий с направления ,  I - единичная матрица, x(t) -  вектор входного сигнала, индексы   (T) и (+) означают транспонирование и эрмитово транспонирование, соответственно. Известно, что оценка направления на L источников внешнего излучения при  использовании адаптивных антенных решеток сводится к нахождению L максимумов следующего функционала

(3)                                                   

где S(f) - вектор фокусировки антенной решетки. Заметим, что использование  функционала  (3) для задач локализации источников известно в литературе также под наименованием метода Кейпона [1,2,4]. 

 

 

3. Быстрые фазовые и амплитудные ошибки.

 

        Предположим,  что l-ый сигнал в k-ом приемном элементе имеет быстрые фазовые и амплитудные сдвиги в первоначальном отклике. Обозначим эти ошибки как  и  . Возмущенный отклик k-ого сенсора может быть записан в виде

 

 

Предположим, что случайные амплитудные и фазовые ошибки имеют нулевое среднее, стационарны и независимы от элемента к элементу, так что дополнительное усреднение по ним даст нам следующее выражение для пространственной ковариационной матрицы

(4)                                                     

где элементы матрицы  равны

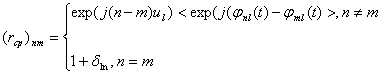
Здесь  - интенсивность амплитудных флуктуаций l-ого сигнала в n-ом приемном элементе. Введем вектор , имеющий компоненты  и перепишем ковариационную матрицу в следующем виде

где  - диагональная матрица. Тогда  может быть представлена в виде

(5)                                                        

где  и . Положим, что амплитудные и фазовые ошибки имеют идентичное статистическое распределение во всех сенсорах. Тогда и вектор  может быть записан в виде. Например, если фазовые ошибки имеют гауссово и независимое от элемента к элементу распределение, то , где  - интенсивность фазовых флуктуаций с l-ого направления. Окончательно, для  пространственной ковариационной матрицы дополнительно усредненной по амплитудным и фазовым флуктуациям  имеем

 

(6)                                       

 

Перепишем выражение (6) в форме аналогичной (2)

(7)                                              

где - мощность эквивалентного собственного шума системы, и

(8)                                                  

- это эквивалентная мощность l-ого внешнего сигнала. Из сравнения (7) и (2) можно видеть, что: 1) фазовые и амплитудные флуктуации эквивалентны увеличению мощности собственного шума и уменьшению мощности внешнего сигнала и ведут к перекачке внешней мощности в мощность собственного шума;

2) для одинаковой интенсивности флуктуаций такая перекачка тем сильнее, чем выше интенсивность падающего сигнала.

Необходимо заметить, что эти качественные выводы справедливы для антенной решетки произвольной геометрии и применимы для анализа любого метода сверхразрешения.  

 

 

  4. Разрешение источников излучения.

 

        Для простоты рассмотрим случай двух внешних источников. Общепринятым критерием разрешающей способности антенной решетки является критерий Релэя, в соответствии с которым два источника одинаковой интенсивности считаются разрешимыми при разнесении в пространстве, если в отклике антенны появляется провал. Т.е. отклик антенны в направлении на любой источник должен быть больше, чем отклик антенны в направлении между источниками. Тогда математически критерий разрешения запишется в виде

(9)                                               

 

Где  – вектор фокусировки антенной решетки между источниками. Для получения аналитических оценок предельной разрешающей способности адаптивной антенны сделаем следующие предположения: а) угловое расстояние между источниками мало по сравнению с шириной главного лепестка; б) источники имеют одинаковую мощность (); с) фазовые и амплитудные ошибки имеют одинаковую интенсивность для обоих сигналов () (это предположение достаточно резонно, если угловое расстояние между источниками мало, и сигналы в процессе распространения проходят по одинаковым неоднородностям среды с одинаковым статистическим распределением).

        Используя эти предположения, на основе подхода, рассмотренного в [9], можно получить, что адаптивная антенная решетка может разрешить два некоррелированных равномощных сигнала, если угловое расстояние между ними не превосходит величину

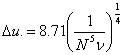
где . Тогда минимальное угловое расстояние в присутствии идентичных фазовых и амплитудных ошибок может быть записано в виде

(10)                                                        

где  определяется аналогично (8). Потери в разрешающей способности из-за наличия флуктуаций запишутся как

(11)                                    

 

Из анализа выражения (11) можно сделать следующие выводы:

1. потери в разрешающей способности адаптивного алгоритма возрастают при увеличении мощности принимаемых сигналов;

2. влияние фазовых флуктуаций на разрешающую способность гораздо существеннее, чем влияние амплитудных флуктуаций.

 

         Таким образом, в настоящей работе изучена потенциальная разрешающая способность адаптивных антенных решеток при наличии случайных и быстрых по сравнению с временем адаптации амплитудных и фазовых ошибок. Показано, что влияние таких флуктуации носит двоякий характер: они приводят к увеличению мощности собственного (пространственно некогерентного) шума, и  одновременно к уменьшению эффективной мощности принимаемых сигналов. При этом влияние фазовых ошибок на разрешающую способность гораздо существеннее, чем амплитудных, особенно для мощных внешних сигналов.

 

Настоящая работа была частично поддержана грантом РФФИ (#02-02-17056).

 

 

5. Список литературы.

 

1.      Гейбриел У. //ТИИЭР, 1980, т.68, №6, с.19-32.

2.      Джонсон  Д. //ТИИЭР, 1982, т.70, №9, с.126-138.

3.      Мюнье Ж., Делиль Ж.Ю. //ТИИЭР, 1987, т.75, №11, с.21-37.

4.       Леховицкий Д.И., Флексер П.М., Атаманский Д.В., Кириллов И.Г. // Антенны, 2000, №2, с. 23-39.

5.      Friedlander B. // IEEE Transactions, November 1990, AES-26, pp.953-968.

6.      Viberg M., Swindlehurst A. // IEEE Transactions, November 1994, SP-42, pp.3073-3083.

7.      Kangas A., Stoica P., Soderstrom T.  // IEE Proc. Radar, Sonar and Navig.,1994, 141, pp.249-255.

8.      Хачатуров В.Р., Федоркин Ю.А., Коновальчик А.С. // Антенны, 2000, №2, с. 55-59.

9.      Серебряков Г.В. // РЭ, 1999, Т.44, №7, С.1041.