"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 5, 2004

оглавление

дискуссия

ДЕКАМЕТРОВЫЕ ИОНОСФЕРНЫЕ ЛИНИИ РАДИОСВЯЗИ С ВЫСОКОЙ ПРОПУСКНОЙ СПОСОБНОСТЬЮ

DECK-METER IONOSPHERIC LINES OF THE RADIO COMMUNICATION WITH HIGH THROUGHPUT

 

Березин Ю.В., Вылегжанин И.С.

Berezin U.V., Vilegzhanin I.S.

(e-mails: berezin@rad564.phys.msu.su, isv1980@yandex.ru)

Московский государственный университет им. М.В.Ломоносова

Получено 17 мая 2004 г.

 

АННОТАЦИЯ

При передаче информации по ионосферному каналу связи (ИКС) с помощью двухлучевого сигнала, вероятность ошибки на приемном конце радиолинии возрастает в десятки раз, а пропускная способность уменьшается на порядок, по сравнению со случаем приема однолучевого сигнала, что является следствием интерференции двух ХВ. Радикально улучшить качество передачи информации по анизотропному ИКС можно, применяя особый метод возбуждения электромагнитных волн на односкачковых линиях радиосвязи. При использовании этого метода на данной радиолинии в ионосфере избирательно возбуждается только одна характеристическая волна, что превращает двухлучевой ИКС в однолучевой и устраняет интерференционные замирания на приемном конце.

Результаты выполненных исследований свидетельствуют, что возможности ионосферного канала связи далеко не исчерпаны – существует большой резерв в его помехоустойчивости и пропускной способности.

 

Актуальность исследования пропускной способности ионосферного канала связи при селективном возбуждении электромагнитных волн в ионосфере Земли обусловлена необходимостью создания новых систем коротковолновой радиосвязи, существенно превосходящих все существующие в настоящее время по скорости и помехоустойчивости передачи информации и обеспечивающих устойчивую радиосвязь с любыми мобильными и стационарными объектами.

Коротковолновая связь с помощью ионосферного канала широко используется в течение многих лет и она обладает целым рядом несомненных достоинств. Но есть у нее и серьезные недостатки, снижающие её значимость – а именно низкая скорость и помехоустойчивость передачи информации. Этот недостаток обусловлен физическими свойствами канала связи – анизотропией ионосферы. Именно структура ионосферы Земли и сложность законов распространения в ней электромагнитных волн не позволяет пока найти научно-технические решения, обеспечивающие достижение потенциальных возможностей в скорости и помехоустойчивости передачи информации по ионосферному каналу связи.

Повышение пропускной способности, помехоустойчивости и скрытности передачи информации по коротковолновым (КВ) линиям радиосвязи может быть достигнуто при использовании:

– параллельных каналов передачи информации;

– широкополосных сигналов;

– пространственно-временного и частотного разноса радиосигналов;

– оптимальных видов модуляции радиоволн при передаче информации.

Все перечисленные направления не обеспечивают радикального решения задачи создания коротковолновых линий радиосвязи, обладающих потенциальными возможностями, которыми располагает ионосферный канал, поэтому поиск оптимальных решений, безусловно, целесообразен.

В последние годы наметилась возможность создания коротковолновых ионосферных линий радиосвязи с высокой помехоустойчивостью и пропускной способностью, которые приближаются к потенциальным.

Ионосферный канал используется для передачи информации на многие тысячи километров и не требует для своего поддержания материальных затрат. Его характерная особенность – это многолучевость, т.е. возможность распространения радиоволны из пункта передачи информации в предполагаемый пункт её приема по нескольким, не совпадающим траекториям, что и ведет, в конечном итоге, к низкой пропускной способности этого канала.

Если найти способ возбуждения радиоволны, обеспечивающий её распространение в ионосфере между пунктами передачи и приема только по одной траектории, то проблема создания оптимальных коротковолновых ионосферных линий радиосвязи будет радикально решена и это откроет новые возможности в использовании ионосферного канала. Такой способ найден, обоснован теоретически, алгоритмически разработан и проверен экспериментально – это метод селективного возбуждения характеристических волн в ионосфере (СВХВ) [1].

Возможности его использования в научных и практических целях пока ещё мало изучены и поэтому все исследования в этой области, безусловно, целесообразны. Данная работа посвящена одной из частных задач, связанных с применением метода СВХВ в ионосфере, а именно с исследованием пропускной способности однолучевой линии декаметровой радиосвязи – самой помехоустойчивой и скоростной из числа тех, которые могут быть реализованы с помощью ионосферного канала.

Реализация метода СВХВ позволяет избавиться от интерференции, обусловленной присутствием двух характеристических (ХВ) в точке приема, на любой радиотрассе (вертикальной или наклонной). При этом на поверхности Земли наименьшее отношение невозбуждаемой ХВ к возбуждаемой достигается в точке приема, для которой осуществляется СВХВ. Этот пункт, в котором отсутствует вторая ХВ, назовем точкой оптимального приема сигнала (ОПС).

При удалении от точки ОПС на приемном конце радиолинии будет увеличиваться отношение невозбуждаемой ХВ к возбуждаемой. В некоторой области вокруг точки оптимального приема мощность одной из волн будет меньше мощности другой волны. Определим границу этой области как линию, на которой отношение мощностей двух ХВ принимает некоторое фиксированное заранее заданное значение Q = Р₁/Р₂, где Р₁ ≤ Р₂ – мощности двух ХВ. Такую область назовем зоной помехоустойчивого приема сигнала (ЗППС).

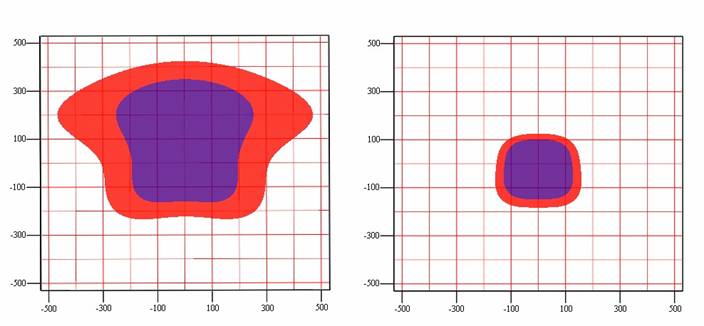
Рис. 1. ЗППС при подавлении необыкновенной (справа) и обыкновенной (слева) характеристических волн. f/fcr = 0,8; геомагнитная широта 55⁰. По осям отложено расстояние от передатчика (координаты (0, 0) км) до приемника – (X, Y) км. Внешние контуры соответствуют значению Q = 1/10, внутренние – 1/20.

 

При разработке сети коротковолновой (КВ) радиосвязи возникает, в частности, задача исследования пропускной способности однолучевых радиолиний, возникающих при использовании метода СВХВ внутри одной ЗППС.

На рисунке 1 представлена ЗППС, полученная для случая вертикального падения электромагнитной волны с частотой f на ионосферу при значении f/f_cr = 0,8, где f_cr – критическая частота.

Видно, что конфигурация, размеры и площади ЗППС при возбуждении в ионосфере обыкновенной или необыкновенной волн заметно различаются.

Важно отметить, что площади ЗППС оцениваются величиной S ~ 100÷200 тыс. кв. км с размером L ~ 350 х 350 км (рассмотрен случай расположения ЗППС на 55⁰ южной геомагнитной широты).

Цель работы: исследовать выигрыш в пропускной способности и помехоустойчивости передачи информации по ионосферной линии связи, приемный пункт которой расположен внутри ЗППС при использовании метода СВХВ.

Для достижения поставленной цели необходимо решить следующие задачи:

1) определить вероятность ошибки при приеме двоичной информации, передаваемой по ионосферной линии связи внутри ЗППС;

2) определить пропускную способность ионосферной линии связи внутри ЗППС;

3) оценить выигрыш в помехоустойчивости и пропускной способности линий связи внутри ЗППС при использовании метода СВХВ в ионосфере.

При вычислении отношения мощностей двух ХВ в ЗППС будем считать, что:

– передача информации осуществляется узкополосным сигналом и свойства радиоволны, пришедшей в точку приема, описываются моделью частично рассеянного поля (ЧРП) [2].

Вероятность ошибки служит количественной мерой помехоустойчивости приема информации. При флуктуациях амплитуды A сигнала средняя вероятность ошибки равна:

,                                                                                                 (1)

где W(A) ‑ функция распределения амплитуды сигнала; h²(A) ‑ отношение сигнал/шум; f(h²) ‑ функция, зависящая от способа передачи информации.

В частном случае некогерентного приема сигналов методом относительной фазовой телеграфии функция f(h²) имеет вид:

,                                                                                                              (2)

где ,  ‑ отношение сигнал/шум: , P_ср - средняя мощность и T - длительность элемента сигнала, - спектральная плотность шума [3].

Чтобы вычислить вероятность ошибки по формуле (1) необходимо знать функцию распределения амплитуды сигнала. Представим электромагнитное поле в пункте приема  в виде суммы произвольного числа ЧРП , причем каждое поле E_i(t) описывается моделью ЧРП; статистическую функцию распределения амплитуды поля W(A) можно вычислить в явном виде для любого числа составляющих E_i(t) [4]. Подставляя функцию W(A) в формулу (1) и интегрируя полученное выражение, приходим к формуле для вероятности ошибки P_err при приеме многолучевого сигнала.

В частности, при приеме двухлучевого сигнала:

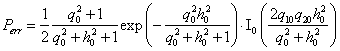,                                                      (3)

где , , , , A_i0 - амплитуда детерминированной составляющей ЧРП,  - дисперсия квадратурной компоненты парциальной волны, - параметр ее рассеяния, I₀ - функция Бесселя нулевого порядка.

При приеме однолучевого сигнала:

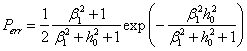,                                                                             (4)

что следует из формулы (3) при отсутствии второй волны.

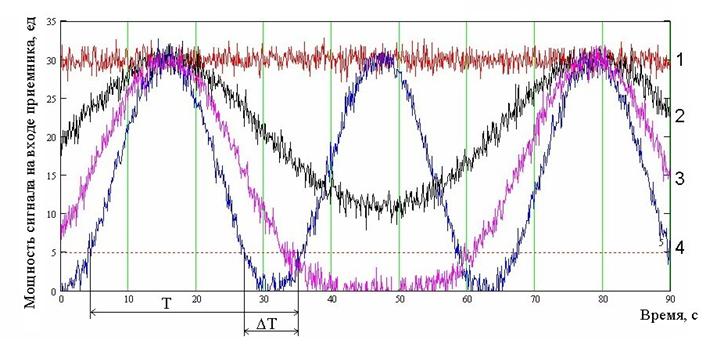
Рис. 2. Мощность суммарного сигнала на входе приемника при приеме двухлучевого поля

1 – на входе приемника присутствует только одна ХВ,

2 – одна ХВ меньше другой в 10 раз (метод СВХВ),

3 – одна ХВ меньше другой в 2 раза,

4 – мощности двух ХВ равны.

 

На рисунке 2 представлен типичный график интерференционных флуктуаций мощности суммы двух ЧРП, доплеровские частотные спектры смещены друг относительно друга на некоторую величину.

В канале связи в полосе приема полезного сигнала всегда присутствует аддитивный шум. Пусть его значение составляет 5 условных единиц, т.е. отношение сигнал/шум (ОСШ) равно 6 (рис. 2, пунктир). Пользуясь графиками рисунка 2 можно наглядно пояснить негативную роль интерференционных замираний суммы двух ХВ в ионосферном канале связи при передаче по нему информации.

Действительно, если мощности двух ХВ равны (кривая 4, рис. 2), то относительное время τ = ΔT/T, где ΔT – время пребывания сигнала ниже уровня шума, Т – период интерференционных замираний суммарного поля, равно приблизительно 30 %. Если мощность одной ХВ в два раза меньше мощности другой, то значение τ также близко к 30 %, и лишь в случае, когда мощность одной ХВ в десять раз меньше другой, суммарная мощность поля (при данном ОСШ) не опускается ниже аддитивного шума (кривая 2, рис. 2).

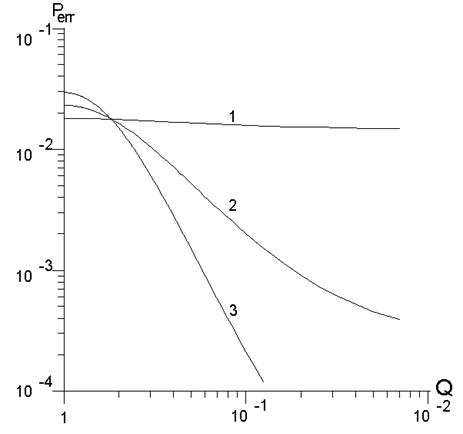
Рис. 3 Зависимость вероятности ошибки от отношения мощностей двух ХВ

(= 1; 10; 25; кривые 1; 2; 3)

Кроме аддитивного шума и значения Q на помехоустойчивость приема информации в ионосферном канале связи (ИКС) влияет также и степень рассеяния сигнала в ионосфере [4]. Негативная роль рассеяния иллюстрируется графиками рисунка 3, на котором изображена зависимость вероятности ошибки Р_err(Q) в функции отношения мощностей двух ХВ при различной степени рассеяния сигнала (параметр = А₀²/< А_P²>, где А₀ и А_P – амплитуды нерассеянной и рассеянной частей принимаемого поля). При вычислении Р_err по формуле (3) было принято значение ОСШ, равное 25.

При сильном рассеянии соотношение мощностей двух ХВ слабо сказывается на вероятности ошибки, которая остается на уровне ~ 10^-2. При большом параметре  (малом рассеянии) с уменьшением величины Q внутри ЗППС вероятность ошибки резко убывает от значения ~ 10^-2 до значения ~ 10^-5 – 10^-6.

Полученные результаты свидетельствуют, что интерференция двух ХВ приводит к резкому снижению помехоустойчивости приема информации (вероятность ошибки при приеме однолучевого и многолучевого сигналов отличаются на несколько порядков).

Значительное уменьшение вероятности ошибки имеет место при значениях Q << 1 и при отношении сигнал/шум  ³ 9. Так, например, значению Q = 1/20 ( = 10,  = 25) соответствует P_err = 10^-3, значению Q = 1/10 – P_err = 2×10^-3. Для сравнения укажем, что при стандартном (неселективном) возбуждении волн в ионосферном канале связи и, например, при Q = 0,5 помехоустойчивость приема оценивается величиной   P_err = 1.6×10^-2. Видно (рис. 1), что с приближением к центру ЗППС уменьшается величина Q (Q для внутреннего контура меньше, чем для внешнего) и, как следствие, вероятность ошибки при передаче информации по ионосферной линии связи приближается к потенциально возможной в данных физических условиях.

Приведенные цифры показывают, что метод селективного возбуждения характеристических волн позволяет уменьшить вероятность ошибки в ионосферном канале связи, как минимум, на порядок.

Ионосферный канал связи, как и любой другой природный канал, является “открытым”, то есть доступным для воздействия со стороны различных помех.

В теории информации базовой “моделью” канала связи является идеальный «гауссовский» канал. В рамках этой модели предполагается, что в канале, кроме полезного сигнала, характеризуемого средней мощностью P_c, присутствует аддитивный шум, являющийся источником искажений передаваемой информации.

Канал связи характеризуется “пропускной способностью”, то есть способностью передавать определенный объем двоичной информации в единицу времени. Пропускная способность идеального гауссовского канала определяется формулой Шеннона [5]:

 бит/с,                                                                                            (5)

где с - пропускная способность канала,  - ширина полосы частот, занимаемая передаваемым сигналом, P_с - средняя мощность сигнала, P_ш - средняя мощность шума в полосе частот .

Формула (5) характеризует предельную скорость передачи информации по каналу связи при заданных параметрах , P_с, P_ш, которая может быть реализована со сколь угодно малыми ошибками на приемном конце канала связи. Формула (5) относится к идеализированному стационарному однолучевому каналу связи и в теории информации не рассматривается возможность ее применения для оценки пропускной способности многолучевого канала.

Для многолучевого канала типичны флуктуации мгновенной мощности принимаемого суммарного поля  и поэтому его пропускная способность также будет зависеть от времени: c = c(t). Для определения пропускной способности многолучевого канала связи решим следующую задачу:

Пусть задан двухлучевой ионосферный канал с определенными свойствами лучей и мощность аддитивного шума N в полосе частот приема .

Необходимо:

1. Найти статистические оценки пропускной способности c = c(t) этого канала.

2. Сравнить пропускную способность двухлучевого канала связи с соответствующей величиной однолучевого канала и оценить выигрыш, который может быть достигнут в результате превращения двухлучевого ионосферного канала связи в однолучевой.

В соответствии с принятой моделью запишем частично рассеянные поля двух ХВ в точке приема:

,     ,                                                                            (6)
где A_1, 2 = const,  = const - амплитуды и доплеровские частоты двух ХВ.

Мгновенная мощность суммарного поля E = E₁ + E₂ , будет равна

,                                                                                         (7)

.

Введем нормированное отношение сигнал/шум по мощности:

.                              (8)

Из формулы (8) следует, что в двухлучевом ионосферном канале связи мгновенное значение отношения сигнал/шум h² = h²(t) есть периодическая функция времени. Используя формулу (8) можно найти интегральную функцию распределения вероятности того, что мгновенное значение h²(t) будет превосходить любое, наперед заданное значение  (рис. 4):

, выразив  из формулы (8) и учитывая, что , получаем:

.                                                                                           (9)

 

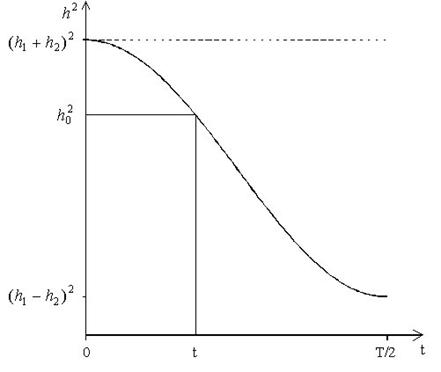
Рис. 4. Зависимость отношения сигнал/шум от времени t для
двухлучевого сигнала (представлена половина периода)

 

Для нахождения статистической характеристики пропускной способности периодически нестационарного двухлучевого ионосферного канала связи необходимо перейти от функции распределения величины  - отношения сигнал/шум в канале связи к функции распределения c(t) - пропускной способности канала связи, что можно сделать по известным правилам [5].

Преобразовав формулу (5) к виду

                                                                                                        (10)
и выполнив преобразование функции , найдем:

,                                                                                         (11)
где , что является следствием перехода от переменной h(t) к переменной c(t) по формуле (9).

Функция (11) зависит от трех параметров - , ,  и характеризует вероятность реализации значения пропускной способности канала c(t) не меньше заданного значения c₀.

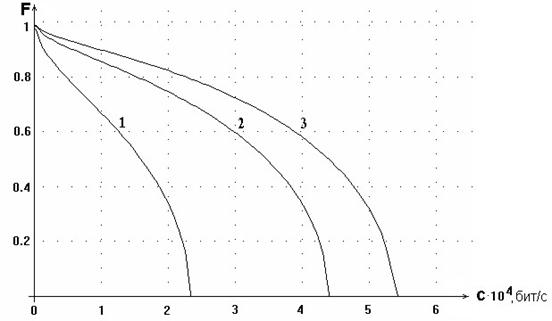
Рис. 5. Интегральная функция распределения пропускной способности двухлучевого канала связи F(c) по параметру . Кривые 1, 2, 3 соответствуют значениям  = 1, 5, 10, ширина полосы частот  = 10 кГц.

 

Анализ формулы (11) и рис. 5 свидетельствуют, что в двухлучевом ионосферном канале связи с вероятностью 90% не может быть реализована скорость передачи информации c₀, превышающая c = 10⁴ бит/с для сигналов с полосой  = 10 кГц даже при соотношении сигнал/шум  = 10.

При  = 1 эти цифры снижаются до значений c = 2×10³ бит/с (для  = 10 кГц).

 

 

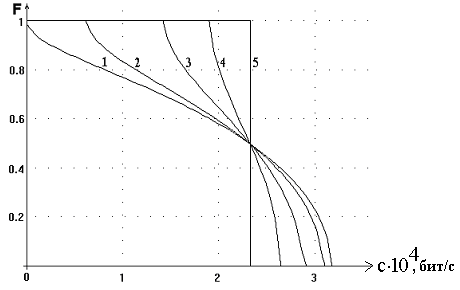
Рис. 6. Интегральная функция распределения пропускной способности двухлучевого канала связи F(c) в зависимости от различного соотношения мощностей двух ХВ при условии , ширина полосы частот  = 10 кГц (параметры кривых 1-5 см. в таблице 1).

 

Семейство графиков (рис. 6) построено для значения  = 10 кГц при различном сочетании мощностей двух ХВ в канале связи и соблюдении условия . Сочетание параметров и номера графиков представлены в таблице 1:

Таблица 1

 

Рис. 6 и таблица 1 показывают, что уменьшение мощности подавляемой ХВ в двухлучевом ионосферном канале связи при помощи СВХВ существенно увеличивает его пропускную способность. Так, например, при равенстве мощностей двух ХВ ( и сигналов с полосой = 10 кГц) с 90% вероятностью можно утверждать, что пропускная способность канала будет меньше значения c = 2×10³ бит/с, а при  и , что соответствует значению Q = 1/10, с той же вероятностью значение c не будет превышать величину 1,4×10⁴ бит/с (кривая 3, рис. 6). Уменьшение Q до 1/40 ( и ) приводит к увеличению c до значения 1.9×10⁴ бит/с, которое приближается к пропускной способности однолучевого канала, в данном случае оценивается величиной c = 2,3×10⁴ бит/с.

Таким образом, в результате выполненных исследований показано, что при передаче информации по реальному односкачковому ионосферному каналу связи помехоустойчивость передачи информации очень сильно зависит от соотношения мощностей двух характеристических волн, неизбежно возникающих в анизотропной ионосфере Земли.

Оценки показывают, что при передаче информации с помощью двухлучевого сигнала, вероятность ошибки на приемном конце радиолинии возрастает в десятки раз, по сравнению со случаем приема однолучевого сигнала, что является следствием интерференции двух ХВ.

Радикально улучшить качество передачи информации по анизотропному ионосферному каналу связи (ИКС) можно, применяя особый метод возбуждения электромагнитных волн на односкачковых линиях радиосвязи. При использовании этого метода на данной радиолинии в ионосфере избирательно (селективно) возбуждается только одна характеристическая волна, что естественно превращает изначально двухлучевой ИКС в однолучевой – со всеми вытекающими из этого обстоятельства следствиями для работы односкачковой линии радиосвязи.

При использовании метода селективного возбуждения характеристических волн (ХВ) для данной радиолинии на поверхности Земли вблизи оптимального пункта приема сигнала возникает значительная зона, внутри которой отношение Q мощностей двух ХВ лежит в пределах значение 0 ≤ Q ≤ 1. Эту зону естественно назвать зоной помехоустойчивого приема сигнала (ЗППС). Очевидно, что пропускная способность всех декаметровых линий  радиосвязи, приемные пункты которых расположены внутри ЗППС, будет зависеть от соотношения мощностей двух ХВ, т.е. от числа Q.

Решение этой задачи привело к следующим выводам:

1)        При традиционном – неселективном – способе возбуждения электромагнитных волн в анизотропном ионосферном канале на односкачковой декаметровой линии радиосвязи ее пропускная способность с вероятностью 90 % не превышает значения c ≤  2×10³ бит/с при отношении сигнал/шум, равном 4 и ширине полосы канала связи , равной 10 кГц.

2)        Использование на односкачковой ионосферной радиолинии нетрадиционного – селективного – способа возбуждения характеристических волн позволяет внутри ЗППС, площадь которых составляет величину ~ 200 тыс. кв. км (средние размеры ЗППС 600 км х 600 км или 300 км х 300 км – в зависимости от типа ХВ), обеспечить пропускную способность всех радиолиний в ЗППС, равной c ≈  20×10³ бит/с при отношении сигнал/шум, равном 4 и ширине полосы канала связи, равной 10 кГц.

3)        Зоны помехоустойчивого приема сигнала для обыкновенной и необыкновенной ХВ имеют различные конфигурацию и площадь, причем ЗППС при возбуждении необыкновенной волны имеет существенно большую площадь, чем ЗППС при возбуждении обыкновенной ХВ.

4)        Конфигурация и площадь ЗППС существенно зависят от геомагнитных координат пункта передачи информации.

Результаты выполненных исследований свидетельствуют, что возможности ионосферного канала связи далеко не исчерпаны – существует большой резерв в его пропускной способности и помехоустойчивости.

 

ЛИТЕРАТУРА:

1.         Березин Ю. В., Балинов В. В., Рыжов Д. Е. Способ возбуждения характеристических электромагнитных волн в ионосфере. Патент РФ № 2002276.

2.    Балинов В.В., Березин Ю.В., Виноградов Ю.Е., Смирнов В.И. Модель частично рассеянного поля с полностью смещенным спектром и помехоустойчивость приема в ионосферном канале связи, Техника средств связи, Сер. СС, 1981, № 2, с. 10-22.

3.    Финк Л.М. Теория передачи дискретных сообщений. М.: Сов. радио, 1970.

4.         Арефьева Л.Н., Березин Ю.В. Функция распределения огибающей и помехоустойчивость приема многолучевых сигналов. Вестник Московского университета. Сер. 3. Физика, Астрономия, 1990, т. 31, № 4, с. 34-37.

4.    Шеннон К. Работы по теории информации и кибернетике: пер. с англ. под ред. Добрушина Р. Л. и Лупанова О. Б. М.: ИЛ. 1963. 829 с.

5.    Левин Б. Р. Теоретические основы статистической радиотехники. М.: Радио и связь, 1989, 653 с.

 

оглавление

дискуссия