УДК 621.372.542
Вероятностно-временные
характеристики процесса
перестройки цифрового синтезатора частоты
М.Ю. Баланов
Московский институт радиотехники, электроники и автоматики
(технический университет)
Получена 4 мая 2008 г.
В статье определяются вероятностно-временные характеристики процесса перестройки цифрового синтезатора частоты на соседнюю частоту. Методом машинного моделирования получены характеристики времени перестройки для некоторых значений частоты генерируемого сигнала. Найдены оценки времени перестройки синтезатора частоты в общем случае.
Цифровой М-ичный синтезатор частоты
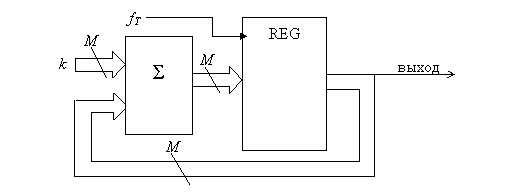
В цифровой обработке сигналов находят применение цифровые синтезаторы частоты, основанные на М-разрядном двоичном счетчике [1]. Структурная схема такого цифрового синтезатора приведена на рис. 1. Состояние Ai регистра REG счетчика меняется с частотой тактового сигнала fТ = 1/T и отображается числом, представленным в двоичной форме с M разрядами. Следующее состояние Ai+1 двоичного счетчика в момент времени (i +1)T определяется его текущим состоянием Ai в момент времени iT и величиной скачка k:
Рис. 1. Структурная схема цифрового синтезатора частоты
Постоянное число k, а также частота тактового сигнала счетчика fТ и разрядность счетчика M определяют частоту сигнала, выдаваемого синтезатором:
Выходной сигнал синтезатора частоты выводится через старший М-й разряд регистра счетчика. Для того, чтобы синтезатор генерировал заданную частоту f, необходимо определить M, fT и k. При фиксированной тактовой частоте fT и разрядности счетчика величина k должна выбираться такой, чтобы частота, выдаваемая синтезатором, была ближайшей к заданной величине. При необходимости перестройки синтезатора на другую частоту достаточно изменить величину скачка k на такую величину, чтобы частота сигнала синтезатора, определяемая (2), снова оказалась ближайшей к необходимому значению.
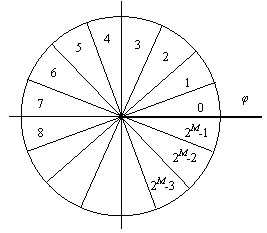
Работа цифрового синтезатора частоты может быть описана с помощью следующего геометрического представления. Круговая фазовая диаграмма (рис.2) делится на 2M равных частей. Каждой части сопоставляется определенное возможное состояние регистра счетчика Ai, последовательно, начиная с 0. Текущее значение фазы генерируемого сигнала соответствует текущей активной части на круговой фазовой диаграмме. Это означает, что значение фазы генерируемого сигнала попадает в отрезок, занимаемый активной частью. На следующем тактовом интервале времени T положение активной части изменяется на k значений против часовой стрелки относительно текущей активной части. Такое изменение активной части соответствует увеличению фазы генерируемого сигнала на 2πk/2M радиан за интервал времени T. Величину k будем называть величиной скачка.
Использование подобного рода цифровых синтезаторов в цифровой обработке сигналов систем связи позволяет существенно упростить блок синхронизации демодулятора, управляя перестройкой синтезатора в соответствии с изменением тактовых и несущих частот принимаемого сигнала.
Рис. 2. Геометрическое представление работы цифрового синтезатора
Анализ процесса перестройки цифрового синтезатора во времени
Процесс перестройки цифрового синтезатора начинается с момента изменения величины скачка k на другое значение, соответствующее новому значению тактовой или несущей частоты принимаемого сигнала, оценка которого получена на выходе частотного детектора или дискриминатора. В условиях большого отношения сигнал/шум принимаемого сигнала и хорошей стабильности частоты наиболее вероятно изменение величины скачка на единичное значение с k до k + 1 или k - 1. Для простоты анализа примем в дальнейшем, что процесс перестройки цифрового синтезатора начинается с момента изменения величины скачка со значения k на значение k+1. Определим, через какой дискретный отрезок времени t скорректированный сигнал на выходе синтезатора будет отличаться от нескорректированного, то есть через какой промежуток времени действительно совершится факт перестройки синтезатора.
Рассмотрим работу двух вспомогательных синтезаторов частот А и Б с одинаковыми начальными состояниями A0 в момент времени t = 0 и величинами скачка k и k+1, соответственно. Сигнал на выходе одного синтезатора А будет соответствовать работе основного синтезатора без перестройки, в то время как ход работы синтезатора Б будет соответствовать перестроенному основному синтезатору. Состояния регистров синтезаторов меняются в соответствии с алгоритмом (1) и величинами скачков k и k+1. Установление факта начала перестройки синтезатора соответствует тому, что в определенный момент времени t количество полных циклов с учетом начального состояния A0, пройденных синтезатором Б превышает на единицу количества полных пройденных циклов синтезатором А, причем в предыдущие моменты t1 < t времени такого отличия не наблюдалось:
где
- целая часть числа х.
Перебор всех возможных начальных состояний A0 позволяет определить характеристики распределения необходимого количества тактов до идентификации факта перестройки синтезатора на новую частоту. Поскольку на практике начало процесса перестройки синтезаторов частоты происходит случайным образом, то можно считать, что начальное состояние регистров A0 является случайным и распределено равновероятно для всех 2М возможных состояний регистра синтезатора частоты.
Аналитического решения системы (3) для заданных A0, M и k найти не удалось, поэтому была построена программно-математическая модель работы двух синтезаторов частоты, в которой определялись вероятностные характеристики времени обнаружения факта перестройки синтезатора частоты на новую частоту.
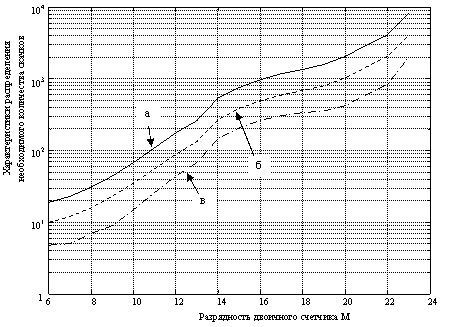
На рис.3 показаны характеристики времени обнаружения факта перестройки синтезатора частоты: математическое ожидание, среднее квадратичное отклонение (СКО) и максимальное значение необходимого числа скачков. Указанные характеристики определены для различных разрядностей M счетчика и таких значений k, которые позволяют получить наиболее близкое значение отношения тактовой и генерируемой частоты к величине fT/f = 18,984375. Время перестройки t измеряется в количестве тактов частоты fT. Из рис.3 следует, что с увеличением разрядности счетчика синтезатора M время обнаружения факта перестройки синтезатора частоты возрастает, причем наблюдается неравномерная скорость роста времени обнаружения на различных участках значений M.
Рис. 3. Характеристики распределения необходимого количества скачков до обнаружения факта перестройки цифрового синтезатора. (а) – максимальное количество скачков, (б) – среднее количество скачков, (в) – СКО необходимого количества скачков. fT/f = 18,984375.
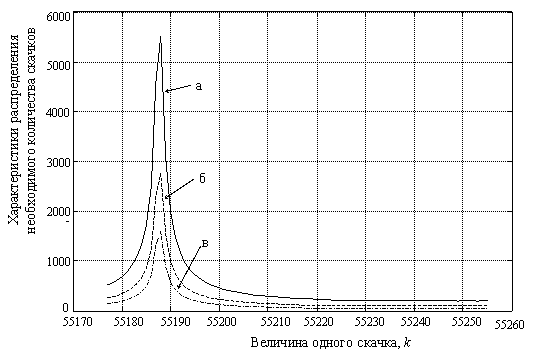
На рис.4 показана зависимость указанных характеристик от величины скачка k при фиксированной разрядности регистра синтезатора M = 20. Указанная разрядность является достаточной для выявления свойств синтезаторов частоты с большой разрядностью. Хотя в целом результаты рис.4 совпадают с результатами рис.3, но для некоторых значений величины скачка k время обнаружения факта перестройки существенно превышает аналогичные показатели для большинства других значений k. В результате проведенных исследований выявлено, что такое аномально высокое увеличение времени обнаружения связано с тем, что отношение тактовой и генерируемой частоты приближается к какому-либо целому значению. Так на рис.4 максимум характеристик времени обнаружения t наблюдается при соотношении fT/f = 19,00007248. Такое явления можно назвать “резонансом” между тактовой и генерируемой частотами. Чем ближе отношение частот к целому числу, тем большим будет время обнаружения факта перестройки синтезатора частоты.
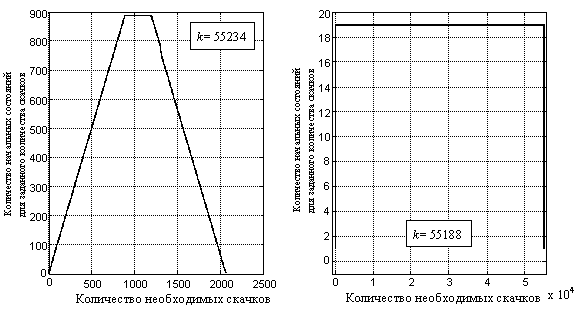
На рис. 5 показано количество начальных состояний регистра синтезатора частоты с заданным временем обнаружения факта перестройки для всевозможных значений t для двух значений величины скачка k = 55234 и k = 55188. Первое значение величины скачка соответствует области значений k со стандартными, “нерезонансными” значениями характеристик времени перестройки синтезатора частоты, второе значение соответствует “резонансному” значению величины скачка k. Заметно значительное отличие двух распределений друг от друга.
Рис.4. Характеристики распределения необходимого количества скачков до обнаружения факта перестройки цифрового синтезатора. (а) – максимальное количество скачков, (б) – среднее количество скачков, (в) – СКО необходимого количества скачков. M = 220.
Рис. 5. Гистограмма распределения необходимого количества скачков до обнаружения факта перестройки генератора при любом равновероятном начальном состоянии регистра генератора. M = 220.
Для малых значений времени обнаружения наблюдается линейная зависимость количества начальных состояний от времени обнаружения. Действительно, для обнаружения факта перестройки уже на следующем тактовом интервале t =1 подходит только одно начальное состояние:
Для определения факта перестройки через интервал времени t =2 существуют уже два начальных состояния:
и
.
Для больших M количество возможных начальных состояний является большой величиной, поэтому вероятность совпадения начальных состояний для t = 1 и t = 2 оказывается малой, а значит, для заданного времени t количество возможных начальных состояний будет с большой долей вероятности равно t. При достижении некоторого порогового значения tпор количество начальных состояний перестает увеличиваться из-за того, что некоторые начальные состояния A0 повторяются снова, так как увеличилась вероятность совпадения начальных состояний для различных t. На рис. 5 для “резонансного” значения k = 55188 пороговое значение tпор оказывается маленьким, а максимальное количество начальных значений на длительном отрезке t соответствует округленному значению отношения fT/f =19.
Определить время, прошедшее с момента перестройки синтезатора до установления факта его перестройки можно другим способом, путем учета разного хода времени для двух синтезаторов. Обозначим N как необходимое количество циклов частоты f до выполнения условия распознавания факта перестройки. Тогда, с учетом (2), время с момента перестройки синтезатора до установления этого факта в структуре сигнала для обоих синтезаторов будет определяться следующими выражениями:
и
. (4)
Минимальная разница во времени Δ между двумя генераторами, которая может быть обнаружена, соответствует периоду тактового сигнала счетчика:
(5)
Максимальное количество скачков частоты f до установления факта перестройки синтезатора равно:
(6)
С учетом связи генерируемой частоты f и тактовой частоты fТ по формуле (2) максимально возможное количество скачков t частоты fT до установления факта перестройки:
Истинное значение необходимого количества скачков до обнаружения факта перестройки может превышать оценку (7) для некоторых значений начального состояния регистра счетчика А0 и некоторых значений величины скачка. На рис. 4 максимальное значение количества скачков до обнаружения факта перестройки равно 55206 для k = 55188, что превышает оценку (7). Количество начальных положений А0, для которых время обнаружения превышает оценку (7), мало, поэтому в большинстве случаев времени по формуле (7) оказывается достаточно для обнаружения факта перестройки.
Если начальным состоянием регистра будет величина А0 = 0, и величина скачка зависит от разрядности счетчика k = 2M-1, то указанное явление “резонанса” будет проявляться максимально, а значит время обнаружения факта перестройки синтезатора частоты достигнет своего максимального значения по формуле (7)
Следует отметить, что для указанного выше случая обнаружение факта перестройки синтезатора частоты возможно через меньшее количество скачков, прежде чем выполняется условие (3). Для примера рассмотрим случай А0 = 0, M = 4, k = 8. Для определенности будем считать, что сигнал на выходе синтезатора принимает единичное значение, если текущее состояние меньше 2M-1, и нулевое значение, если текущее состояние больше или равно 2M-1. В табл.1 показан во времени процесс перестройки синтезатора частоты в рассматриваемом случае.
Таблица 1
Номер скачка
Значение регистра k счетчика
Значение регистра k+1 счетчика
Количество полных циклов k счетчика
Количество полных циклов k+1 счетчика
Состояние на выходе k синтезатора
Состояние на выходе k+1 синтезатора
0
0
0
0
0
1
1
1
8
9
0
0
0
0
2
0
2
1
1
1
1
3
8
11
1
1
0
0
4
0
4
2
2
1
1
5
8
13
2
2
0
0
6
0
6
3
3
1
1
7
8
15
3
3
0
0
8
0
8
4
4
1
0
9
8
1
4
5
0
1
Из табл. 1 следует, что хотя условие (3) выполняется только на девятом такте, сигналы на выходе синтезаторов отличаются уже на восьмом такте. Это связано с тем, что формальное количество полных циклов для двух генераторов совпадает, но для второго синтезатора полный цикл на восьмом шаге оказывается виртуальным, и выходной сигнал повторяет предыдущее нулевое значение, поскольку шаг перестройки для этого синтезатора оказывается больше половины числа возможных состояний счетчика.
Рассмотренный выше анализ хода перестройки цифрового синтезатора частоты справедлив в случае, если генерируемая частота k синтезатора и k+1 синтезатора не превышает половины тактовой частоты и появление “виртуальных” полных циклов счетчика оказывается невозможным. Обычно при цифровой обработке сигналов данное соотношение выполняется как следствие теоремы Котельников.
Заключение
Исследование процесса перестройки цифрового синтезатора частоты позволило оценить время обнаружения факта перестройки. В большинстве случаев оно будет намного меньше его верхней оценки. При приближении к целому значению отношения тактовой частоты к частоте генерации наблюдается существенное увеличение времени обнаружения факта перестройки синтезатора частоты. Процесс перестройки синтезатора частоты на новую частоту носит дискретный характер.
Литература
1. Goldberg B.-G. Digital frequency synthesis demystified. – Eagle Rock, Virginia: LLH Technology Publishing, 1999. – 336 p.
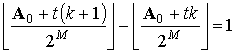 и
и 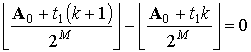
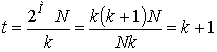 (7)
(7)