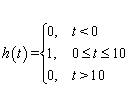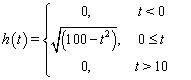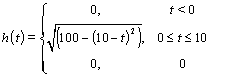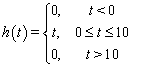Об использовании сверхширокополосных сигналов для идентификации радиолокационных объектов
Н.
П. Чубинский, В. В. Кирьяшкин, Н. К. Хи
Московский физико-технический институт (государственный университет)
Получена 30 апреля 2010 г.
Аннотация. Рассмотрены подходы к задаче
распознавания радиолокационных целей. Показано, что использование для
радиолокации сверхширокополосных (СШП) сигналов представляется в этом смысле
достаточно перспективным. Сформулированы приближённые способы решения
поставленной задачи для плоских и осесимметричных объектов, опирающиеся на
использование короткого СШП радиосигнала в виде производной ![]() -функции. Кроме того, для определения формы
осесимметричных объектов предложено развитие метода профильных функций
Кенно-Моффата.
-функции. Кроме того, для определения формы
осесимметричных объектов предложено развитие метода профильных функций
Кенно-Моффата.
Ключевые слова: радиолокация
широкополосных сигналов, функции Кенно-Моффата.
1. Введение
В классической
относительно узкополосной радиолокации пространственная длительность
излучаемого цуга электромагнитных волн, как правило, заметно больше
геометрических размеров наблюдаемых объектов, а угловые размеры объектов –
существенно меньше эффективной ширины диаграммы направленности антенн. В этом
случае объект отображается в виде точки, а его геометрическая конфигурация
никак не влияет на параметры отражённого сигнала. Идентификация объектов может
быть осуществлена очень грубо по вторичным признакам: средней величине
эффективной поверхности рассеяния ![]() (ЭПР), радиальной относительной скорости
(ЭПР), радиальной относительной скорости![]() и т. п. Для повышения
информативности радиолокационного обнаружения и идентификации объектов (с
близкими величинами ЭПР) активно используют сверхширокополосные (СШП) сигналы
[1]. Например, излучённый СШП радиоимпульс
и т. п. Для повышения
информативности радиолокационного обнаружения и идентификации объектов (с
близкими величинами ЭПР) активно используют сверхширокополосные (СШП) сигналы
[1]. Например, излучённый СШП радиоимпульс ![]() минимальной длительности имеет
относительную ширину спектра около октавы
минимальной длительности имеет
относительную ширину спектра около октавы![]() , где,
, где, ![]()
![]() – верхняя и нижняя частоты спектра. Во
временной области этому соответствует сигнал с эффективной длительностью
– верхняя и нижняя частоты спектра. Во
временной области этому соответствует сигнал с эффективной длительностью ![]() , 90% энергии которого
сосредоточено в двух полупериодах (полуволнах) разной полярности.
Пространственную длительность СШП сигнала
, 90% энергии которого
сосредоточено в двух полупериодах (полуволнах) разной полярности.
Пространственную длительность СШП сигнала ![]() будем предполагать гораздо меньшей по
сравнению с характерными размерами исследуемого радиолокационного объекта
будем предполагать гораздо меньшей по
сравнению с характерными размерами исследуемого радиолокационного объекта ![]() . В этом случае,
возможно резко повысить информативность рассеянного объектом сигнала, выделив в
отражённом сигнале отдельные компоненты с разным запаздыванием. Они обусловлены
так называемыми «блестящими» точками, краевыми и угловыми волнами [2].
. В этом случае,
возможно резко повысить информативность рассеянного объектом сигнала, выделив в
отражённом сигнале отдельные компоненты с разным запаздыванием. Они обусловлены
так называемыми «блестящими» точками, краевыми и угловыми волнами [2].
Как известно, регистрируемый сигнал в классической относительно узкополосной радиолокации представляет собой свертку зондирующего сигнала с импульсной характеристикой радиолокационного объекта:
где![]() – зондирующий (излучаемый) сигнал,
– зондирующий (излучаемый) сигнал, ![]() -- импульсная характеристика
объекта, которые считаются финитными функциями. Влиянием среды распространения
в этом случае можно пренебречь. При использовании СШП сигналов нельзя
пренебрегать в общем случае дисперсионными свойствами среды распространения.
Аналогично должны быть учтены частотные свойства антенны (антенн)
радиолокатора. Тогда соотношение (1) следует представить в виде цепочки
свёрток:
-- импульсная характеристика
объекта, которые считаются финитными функциями. Влиянием среды распространения
в этом случае можно пренебречь. При использовании СШП сигналов нельзя
пренебрегать в общем случае дисперсионными свойствами среды распространения.
Аналогично должны быть учтены частотные свойства антенны (антенн)
радиолокатора. Тогда соотношение (1) следует представить в виде цепочки
свёрток:
где ![]() – сигнал возбуждения излучающей антенны,
– сигнал возбуждения излучающей антенны, ![]() – импульсная
характеристика излучающей антенны,
– импульсная
характеристика излучающей антенны,![]() – импульсная характеристика среды
распространения,
– импульсная характеристика среды
распространения, ![]() –
импульсная характеристика объекта и
–
импульсная характеристика объекта и ![]() – импульсная характеристика приёмной
антенны и приёмника [3] (в наиболее распространённой однопозиционной
радиолокации
– импульсная характеристика приёмной
антенны и приёмника [3] (в наиболее распространённой однопозиционной
радиолокации ![]() ).
В частотной области это эквивалентно произведению соответствующих частотных
характеристик.
).
В частотной области это эквивалентно произведению соответствующих частотных
характеристик.
Однако в работе [3] и многих других
не всегда учитывается тот важный факт, что импульсная характеристика объекта и
связанная с ней частотная характеристика зависят от ракурса его облучения и
наблюдения. Она имеет очень сложную пространственную структуру, содержащую
сотни и тысячи локальных экстремумов. Это определяется сложностью угловых
зависимостей ЭПР объектов больших электрических размеров, как при обратном и
тем более двухпозиционном обнаружении. Тогда для полноценной идентификации
радиолокационного объекта только при однопозиционной регистрации необходимо
найти ![]() во всём
угловом пространстве и в диапазоне времён задержки
во всём
угловом пространстве и в диапазоне времён задержки ![]() по измеренному массиву сигналов
по измеренному массиву сигналов ![]() в ограниченном
диапазоне ракурсов облучения, зная форму излучённого сигнала
в ограниченном
диапазоне ракурсов облучения, зная форму излучённого сигнала ![]() и ракурсы, под которыми
зарегистрированы сигналы. Здесь
и ракурсы, под которыми
зарегистрированы сигналы. Здесь ![]() – максимальная протяжённость объекта
(группы объектов) в направлении зондирования. Возможность полного решения такой
задачи в настоящее время является весьма сомнительной.
– максимальная протяжённость объекта
(группы объектов) в направлении зондирования. Возможность полного решения такой
задачи в настоящее время является весьма сомнительной.
Более продуктивным представляется приближённый подход, суть которого заключается в следующем. Проводится моделирование обратного отражения максимально упрощённых СШП радиосигналов, удовлетворяющих принципу Рэлея, от объектов простейшей формы: плоских (прямоугольная, трапецеидальная, круглая, эллиптическая и треугольная пластины) и объёмных (шар, эллипсоид, конус, пирамида, призма, параллелепипед). Анализируется динамика изменения импульсной характеристики в широком диапазоне ракурсов и устанавливаются основные закономерности их изменений в ограниченных диапазонах углов наблюдения. Строятся алгоритмы идентификации, связанные с определением максимального числа геометрических параметров простейших целей и предельные возможности для различных случаев обнаружения. Только потом можно обратиться к более сложным объектам, близким по геометрии к интересующим целям.
Эта работа является
началом решения поставленной выше задачи. Под СШП сигналом будем понимать
сигнал с относительной шириной спектра ![]() около октавы
около октавы ![]() , где
, где![]() ,
, ![]() – верхняя и нижняя частоты спектра.
Сигналы будем исследовать во временной области. Рассмотрим сигнал, состоящий из
двух полуволн разной полярности, удовлетворяющий критерию Рэлея.
Пространственную длительность СШП сигнала будем предполагать гораздо меньшей по
сравнению с характерными размерами исследуемого радиолокационного объекта.
Пространственное расстояние между значениями времени, соответствующими
максимуму и минимуму сигнала будем называть полупериодом сигнала
– верхняя и нижняя частоты спектра.
Сигналы будем исследовать во временной области. Рассмотрим сигнал, состоящий из
двух полуволн разной полярности, удовлетворяющий критерию Рэлея.
Пространственную длительность СШП сигнала будем предполагать гораздо меньшей по
сравнению с характерными размерами исследуемого радиолокационного объекта.
Пространственное расстояние между значениями времени, соответствующими
максимуму и минимуму сигнала будем называть полупериодом сигнала ![]() .
.
2. Суть метода
Как известно, принимаемый сигнал представляет собой свертку зондирующего сигнала с импульсной характеристикой радиолокационного объекта:
![]() ,
,
где ![]() – зондирующий (излучаемый) сигнал,
– зондирующий (излучаемый) сигнал, ![]() – импульсная
характеристика объекта. Влиянием трассы распространения на результирующий
сигнал пренебрегаем. Функции
– импульсная
характеристика объекта. Влиянием трассы распространения на результирующий
сигнал пренебрегаем. Функции ![]() и
и ![]() – финитные.
– финитные.
Как правило, для
идентификации радиолокационных объектов необходимо определить![]() по известным
по известным ![]() и
и ![]() . Суть предлагаемого в настоящей
работе метода заключается в следующем. Заметим, что очень короткий, состоящий
из двух полупериодов сигнал, имеет сходство с производной
. Суть предлагаемого в настоящей
работе метода заключается в следующем. Заметим, что очень короткий, состоящий
из двух полупериодов сигнал, имеет сходство с производной ![]() -функции. Таким образом,
принимаемый сигнал
-функции. Таким образом,
принимаемый сигнал ![]() можно
интерпретировать как разность функций
можно
интерпретировать как разность функций ![]() сдвинутых на полупериод сигнала
сдвинутых на полупериод сигнала ![]() , или приближенно как
производную функции
, или приближенно как
производную функции ![]() .
Тогда:
.
Тогда:
Сделаем еще одно
замечание: как следует из свойств свертки, для финитных функций длительность
результирующего сигнала ![]() равна сумме длительностей
равна сумме длительностей ![]() и
и ![]() .
.
Чтобы можно было рассматривать ![]() как производную
как производную ![]() -функции необходимо
выполнение некоторых условий. В частности, длительность
-функции необходимо
выполнение некоторых условий. В частности, длительность ![]() должна быть такова, чтобы
изменение функции
должна быть такова, чтобы
изменение функции ![]() на
протяжении каждой из полуволн функции
на
протяжении каждой из полуволн функции ![]() было достаточно малым.
было достаточно малым.
3. Иллюстрирующие расчеты
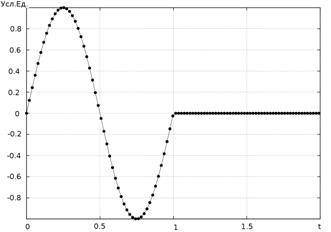
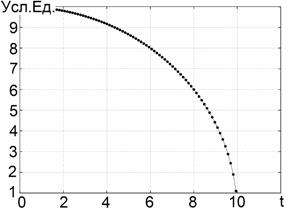
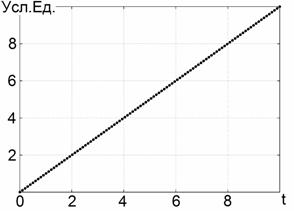
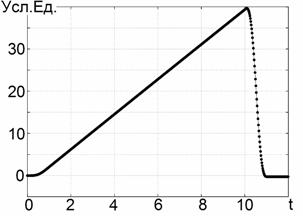
В качестве простейшего модельного зондирующего сигнала выберем отрезок синусоиды, показанный на Рис. 1:
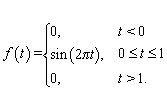
Эффективная относительная ширина
спектра такой (к сожалению, физически нереализуемой) функции [4] – ![]() , что позволяет уверенно
относить её к сверхширокополосным сигналам. В качестве функции
, что позволяет уверенно
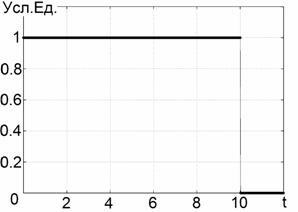
относить её к сверхширокополосным сигналам. В качестве функции ![]() выберем несколько элементарных
функций, имеющих длительностью, например, в 10 раз больше, чем зондирующий
сигнал (4) – левая колонка Таблицы 1. В коротковолновом приближении импульсная
характеристика (4) приближённо соответствует обратному рассеянию от
прямоугольного проводящего объекта при облучении его в плоскости симметрии. Её
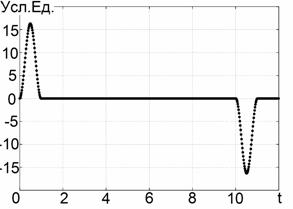
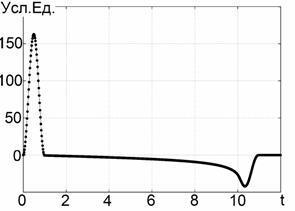
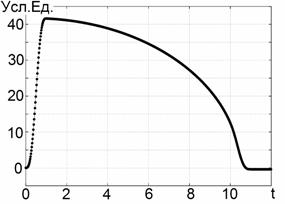
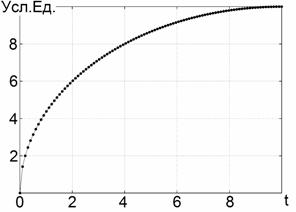
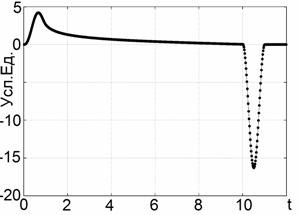
график представлен на Рис. 2а. На Рис. 2б приведён регистрируемый сигнал,
построенный согласно (1). Характерной особенностью обратного рассеяния от
прямоугольной апертуры является то, что отражённый сигнал содержит две
составляющие в виде полупериода излучаемого сигнала разной полярности. Физически
они представляют собой краевые волны: первую, относящуюся к рассеянию на
передней кромке прямоугольника, и вторую, которая
выберем несколько элементарных
функций, имеющих длительностью, например, в 10 раз больше, чем зондирующий
сигнал (4) – левая колонка Таблицы 1. В коротковолновом приближении импульсная
характеристика (4) приближённо соответствует обратному рассеянию от
прямоугольного проводящего объекта при облучении его в плоскости симметрии. Её
график представлен на Рис. 2а. На Рис. 2б приведён регистрируемый сигнал,
построенный согласно (1). Характерной особенностью обратного рассеяния от
прямоугольной апертуры является то, что отражённый сигнал содержит две
составляющие в виде полупериода излучаемого сигнала разной полярности. Физически
они представляют собой краевые волны: первую, относящуюся к рассеянию на
передней кромке прямоугольника, и вторую, которая
определяется его задней кромкой. Причём длительность каждого отклика в два раза
превышает длительность полупериода излучённого сигнала. Как нетрудно убедиться,
что каждая составляющая на Рис. 2б качественно близка к разности функций ![]() , сдвинутых на
полупериода зондирующего сигнала
, сдвинутых на
полупериода зондирующего сигнала ![]() . Причём длительность рассеянного сигнала
. Причём длительность рассеянного сигнала![]() равна сумме
длительности импульсной характеристики
равна сумме
длительности импульсной характеристики ![]() и длительности излучённого сигнала
и длительности излучённого сигнала ![]() .
.
Пользуясь соотношением (3),
восстановим ![]() ,
проинтегрировав
,
проинтегрировав ![]() по
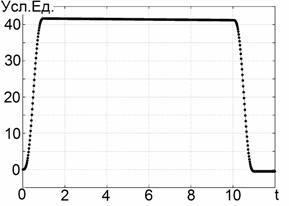
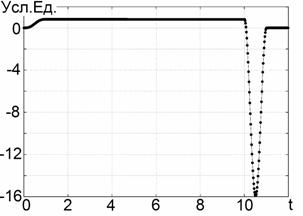
времени. Нетрудно видеть, что восстановленный сигнал (Рис.2в) имеет
удовлетворительное сходство с оригиналом на Рис. 2а. Это сходство будет тем
более точным, чем меньше длительность зондирующего сигнала (то есть, чем ближе
функция
по
времени. Нетрудно видеть, что восстановленный сигнал (Рис.2в) имеет
удовлетворительное сходство с оригиналом на Рис. 2а. Это сходство будет тем
более точным, чем меньше длительность зондирующего сигнала (то есть, чем ближе
функция ![]() к
производной d-функции).
к
производной d-функции).
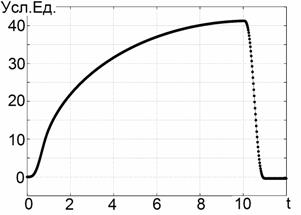
Выберем теперь в качестве ![]() другую импульсную
характеристику (5) – правая колонка Таблицы 1, – которая показана на
Рис 3а.
Качественно она соответствует обратному рассеянию от половины проводящего эллипса,
облучаемого со стороны прямой кромки в плоскости симметрии. Вид регистрируемого
сигнала
другую импульсную
характеристику (5) – правая колонка Таблицы 1, – которая показана на
Рис 3а.
Качественно она соответствует обратному рассеянию от половины проводящего эллипса,
облучаемого со стороны прямой кромки в плоскости симметрии. Вид регистрируемого
сигнала ![]() дан на
Рис. 3б. Также как и в предыдущем случае рассеянный сигнал формируется краевыми
волнами, отражёнными от передней (прямой) кромки и задней (овальной) кромки.
Амплитуда сигнала, формируемого передней широкой кромкой, существенно
превосходит сигнал от задней.
дан на
Рис. 3б. Также как и в предыдущем случае рассеянный сигнал формируется краевыми
волнами, отражёнными от передней (прямой) кромки и задней (овальной) кромки.
Амплитуда сигнала, формируемого передней широкой кромкой, существенно
превосходит сигнал от задней.
График восстановленной
импульсной характеристики ![]() половины эллипса представлен на
Рис. 3в
правой колонки Таблицы 1. даже при достаточно грубом представлении наблюдается
убедительное сходство модельной функции (Рис. 3а) и её реконструкции.
половины эллипса представлен на
Рис. 3в
правой колонки Таблицы 1. даже при достаточно грубом представлении наблюдается
убедительное сходство модельной функции (Рис. 3а) и её реконструкции.
Выберем теперь в качестве
![]() другие
импульсные характеристики: (6) – левая колонка, (7) – правая колонка
Таблицы 2.
Первая из них качественно соответствует рассеянию от половины проводящего эллипса,
облучаемого со стороны овальной кромки в плоскости симметрии (с
противоположного направления по отношению к последнему случаю), вторая
относится к рассеянию от проводящего равнобедренного треугольника, облучаемого
со стороны вершины в плоскости симметрии. На Рис. 4а и
Рис. 5а показаны
модельные импульсные характеристики. По аналогии с вышеизложенным, на
Рис. 4б и
Рис. 5б приведены формы отраженных сигналов, рассчитанных по
(1). На Рис. 4в и
Рис. 5в даны восстановленные с помощью (3) импульсные характеристики. И в этих
случаях наблюдается убедительное сходство модельных функций и их реконструкций.
Во всех рассмотренных выше случаях рассеивающие объекты являлись плоскими
(двумерными).
другие
импульсные характеристики: (6) – левая колонка, (7) – правая колонка
Таблицы 2.
Первая из них качественно соответствует рассеянию от половины проводящего эллипса,
облучаемого со стороны овальной кромки в плоскости симметрии (с
противоположного направления по отношению к последнему случаю), вторая
относится к рассеянию от проводящего равнобедренного треугольника, облучаемого
со стороны вершины в плоскости симметрии. На Рис. 4а и
Рис. 5а показаны
модельные импульсные характеристики. По аналогии с вышеизложенным, на
Рис. 4б и
Рис. 5б приведены формы отраженных сигналов, рассчитанных по
(1). На Рис. 4в и
Рис. 5в даны восстановленные с помощью (3) импульсные характеристики. И в этих
случаях наблюдается убедительное сходство модельных функций и их реконструкций.
Во всех рассмотренных выше случаях рассеивающие объекты являлись плоскими
(двумерными).
4. Связь импульсной характеристики с формой объекта
Попытаемся проанализировать связь формы принимаемого сигнала с формой трехмерных объектов. Так как информация о зондируемых объектах содержится в импульсных характеристиках, то нам необходимо оценить геометрические характеристики объектов, используя ограниченный массив зарегистрированных сигналов.
Вследствие того, что
временная длительность импульсной характеристики объекта не может быть больше
пространственной протяженности объекта в направлении распространения падающей
волны, отнесенной к скорости распространения волны, оказывается возможным
сделать оценку снизу соответствующих геометрических размеров объекта в
указанном направлении. А именно: указанная протяженность объекта не меньше, чем
![]() , где
, где ![]() – длительность
принятого сигнала. Зондируя объект под разными углами и получая соответствующие
значения оценочной протяженности объекта, можно сделать некоторые выводы о
форме объекта. Указанная методика может быть реализована на практике, так как
диапазон наблюдения объекта, как правило, составляет порядка 90°. Однако, вследствие того, что
реальные объекты наблюдения имеют сложную геометрическую форму и такие оценки
протяженности объекта могут оказаться достаточно грубыми, указанная методика в
чистом виде скорее всего может играть только вспомогательную роль в решении
задачи определения формы объекта.
– длительность
принятого сигнала. Зондируя объект под разными углами и получая соответствующие
значения оценочной протяженности объекта, можно сделать некоторые выводы о
форме объекта. Указанная методика может быть реализована на практике, так как
диапазон наблюдения объекта, как правило, составляет порядка 90°. Однако, вследствие того, что
реальные объекты наблюдения имеют сложную геометрическую форму и такие оценки
протяженности объекта могут оказаться достаточно грубыми, указанная методика в
чистом виде скорее всего может играть только вспомогательную роль в решении
задачи определения формы объекта.
Таким образом, хотелось бы иметь методы, позволяющие по форме импульсной характеристики делать выводы о геометрической форме объекта. Одним из возможных подходов является метод физической оптики. Этот подход восходит к [5, 6] и упоминается в [3,8]. Опишем его здесь вкратце.
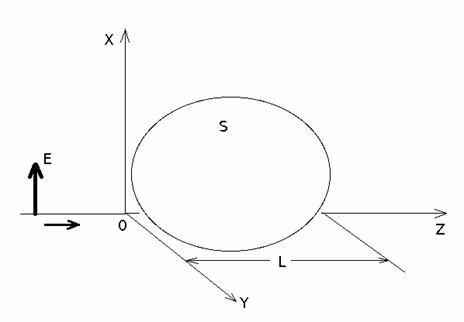
Будем рассматривать поле
рассеяния только в дальней зоне (облучающая радиоволна считается плоской в
пределах максимального поперечного сечения объекта) и ограничимся случаем
только обратного рассеяния. Рассмотрим плоскую линейно-поляризованную волну,
падающую на идеально проводящий объект (Рис. 6). Считаем, что поляризация поля
обратного рассеяния параллельна поляризации
падающей плоской волны. Пусть объект лежит справа от плоскости (XOY) и имеет
протяженность от z=0 до z=L, кроме того, пусть выполнены условия приближения
Кирхгофа. В принятых предположениях, как показано в [3,
5-8] оказывается, что
импульсная характеристика ![]() пропорциональна второй производной по z от
так называемой профильной функции
пропорциональна второй производной по z от
так называемой профильной функции ![]() исследуемого объекта:
исследуемого объекта:
![]() ,
,
где ![]() . Профильную функцию можно определить как
площадь сечения объема исследуемого объекта плоскостью, параллельной фронту
падающей плоской волны, при условии
. Профильную функцию можно определить как
площадь сечения объема исследуемого объекта плоскостью, параллельной фронту
падающей плоской волны, при условии ![]() в областях тени, поскольку мы работаем в
коротковолновом приближении. В этом случае поверхностные токи в области тени
затухают на расстоянии порядка (5…7) λ, где λ — средняя длина волны
спектра излученного сигнала. То есть, импульсная характеристика
в областях тени, поскольку мы работаем в
коротковолновом приближении. В этом случае поверхностные токи в области тени
затухают на расстоянии порядка (5…7) λ, где λ — средняя длина волны
спектра излученного сигнала. То есть, импульсная характеристика ![]() представляет собой
сигнал, кратный второй производной от
представляет собой
сигнал, кратный второй производной от ![]() [5, 7], изменяющийся во времени так, чтобы
секущая плоскость, используемая для определения
[5, 7], изменяющийся во времени так, чтобы
секущая плоскость, используемая для определения ![]() , перемещалась со скоростью, равной
половине скорости движения падающей импульсной волны.
, перемещалась со скоростью, равной
половине скорости движения падающей импульсной волны.
Таким образом,
оказывается возможным по принятому сигналу сделать заключения об изменении
площади поперечного сечения исследуемого объекта в направлении распространения
падающей волны путем двукратного интегрирования полученной функции ![]() . Этот подход также
имеет некоторые ограничения, вытекающие из использования приближения Кирхгофа и
предположения о выпуклости исследуемого объекта (что в большинстве практически
интересных случаев не выполняется). Также этот способ не дает возможности
однозначно определить истинную форму и ориентацию объекта в пространстве
вследствие невозможности получения информации о скрытых в области тени частях
объекта. Для восстановления формы объекта представляется полезным использовать
данный метод для ряда ракурсов, например, зондируя перемещающийся объект на
протяжении некоторого участка его траектории. Информация, полученная в
результате такого зондирования, позволяет восстановить некоторые участки
объекта, находившиеся в предыдущих ракурсах в области «тени». Математическое
оформление указанных соображений является предметом дальнейших исследований.
. Этот подход также
имеет некоторые ограничения, вытекающие из использования приближения Кирхгофа и
предположения о выпуклости исследуемого объекта (что в большинстве практически
интересных случаев не выполняется). Также этот способ не дает возможности
однозначно определить истинную форму и ориентацию объекта в пространстве
вследствие невозможности получения информации о скрытых в области тени частях
объекта. Для восстановления формы объекта представляется полезным использовать
данный метод для ряда ракурсов, например, зондируя перемещающийся объект на
протяжении некоторого участка его траектории. Информация, полученная в
результате такого зондирования, позволяет восстановить некоторые участки
объекта, находившиеся в предыдущих ракурсах в области «тени». Математическое
оформление указанных соображений является предметом дальнейших исследований.
Выводы
Таким образом,
предлагается метод определения импульсной характеристики радиолокационных
объектов, основанный на интерпретации зондирующего СШП сигнала как приближения
производной ![]() -функции.
Указаны требования к зондирующему сигналу для корректного использования
предлагаемого подхода. Приведены результаты иллюстрирующих расчетов для
простейших импульсных функций. Показана продуктивность предлагаемого метода.
Указан способ приближенного определения формы объекта по вычисленной импульсной
функции для конкретного ракурса облучения. Изложены соображения, позволяющие
уточнить получаемые результаты путем многократной регистрации рассеянного
объектом сигнала в интервале ракурсов 90°…120°,
что может оказаться достаточным для идентификации реальных объектов.
-функции.
Указаны требования к зондирующему сигналу для корректного использования
предлагаемого подхода. Приведены результаты иллюстрирующих расчетов для
простейших импульсных функций. Показана продуктивность предлагаемого метода.
Указан способ приближенного определения формы объекта по вычисленной импульсной
функции для конкретного ракурса облучения. Изложены соображения, позволяющие
уточнить получаемые результаты путем многократной регистрации рассеянного
объектом сигнала в интервале ракурсов 90°…120°,
что может оказаться достаточным для идентификации реальных объектов.
ЛИТЕРАТУРА
1. Кошелев В.И., Шипилов С.Э., Якубов В.П. Восстановление формы объектов при малоракурсной сверхширокополосной радиолокации // РЭ. Т. 44, № 3, с. 301-305. 1999
2. Нгуен К.Х., Чубинский Н.П. Особенности радиолокационного рассеяния сверхширокополосного импульсного сигнала прямоугольной пластиной // Тр. РНТОРЭС им А.С. Попова, Вып. 65 . Москва, 14-15 мая, 2008, с. 329-331
3. Астанин Л.Ю., Костылев А.А. Основы сверхширокополосных радиолокационных измерений. М.: Радио и связь 1989 – 192 стр.
4. Финкельштейн М.И., Мендельсон В.Л., Кутев В.А. Радиолокация слоистых земных покровов. Под. Ред. М.И. Финкельштейна. М.: Сов. Радио, 1977, 176 с.
5. Kennaugh E.M., Moffatt D.L. Transient and impuls response approximations // Proc. IEEE, № 8, p. 893-901, 1965
6. Кенно, Моффат. Аппроксимации переходных и импульсных переходных характеристик // ТИИЭР. -- 1965. -- Т.53, № 8. -- С. 1025-1034.
7. Moffat D.L., Mains R.K. Detection and discrimination of radar targets // IEEE Trans. AP-23, p. 358-367, 1975
8. Исследование объектов с помощью пикосекундных импульсов. Под ред. проф. Г.В.Глебовича., М: Радио и связь, 1984.
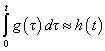 . (3)
. (3)