УДК 621.396
ИДЕНТИФИКАЦИОННЫЙ МЕТОД ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
Ю. Н. Кликушин
Омский государственный технический университет
Получена 30 апреля 2010 г.
Аннотация. Описан метод цифровой обработки сигналов, ориентированный на решение задачи вторичной дискретизации. Суть метода заключается во введении автоматического регулирования интервала дискретизации в зависимости от результатов идентификационных измерений формы входного и выходного сигналов.
Ключевые слова: алгоритм, идентификационная эквивалентность, инструменты, метод, цифровая обработка сигналов.
ВВЕДЕНИЕ
При цифровой обработке сигналов (ЦОС) очень часто возникает необходимость переноса спектра сигнала из высокочастотной в низкочастотную область. Наиболее просто данная задача решается с помощью вторичной дискретизации, физический смысл которой состоит в увеличении интервалов времени между отсчетами выборочной реализации [1].
В современных программных системах ЦОС и анализа данных, например, LabVIEW, имеются соответствующие инструменты (например, Align & Resample.vi) для реализации указанной функции. Однако, для корректного практического использования этих инструментов, требуются дополнительные (априорные) знания о форме входного сигнала, поскольку от этого напрямую зависит эффективность преобразования. При этом, пользователь должен знать заранее, какую максимальную длительность интервала дискретизации можно задать, а какую – нет, с тем, чтобы сигнал можно было восстановить, например, линейным полиномом, с заданной погрешностью [2].
Возможность непосредственного учета информации о форме входного сигнала в числовом виде, по мнению автора, заложена в теории идентификационных измерений, поскольку содержанием этой теории является измерение формы и вариабельности сигналов [3].
В данной работе описаны инструменты и технологии применения идентификационного метода вторичной дискретизации, которые могут быть использованы для построения аппаратно-программных средств ЦОС.
МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЯ
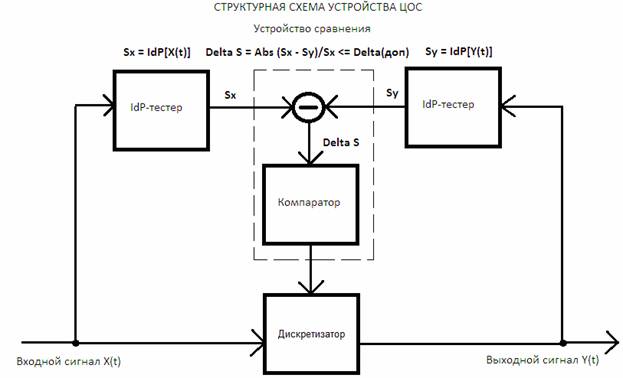
Методика исследований основана на компьютерном моделировании структурной схемы (рис. 1). Структурная схема модели устройства ЦОС содержит два идентификационных тестера (IdP-тестер), устройство сравнения и дискретизатор. Левый по схеме идентификационный тестер (IdP-тестер) измеряет форму распределения входного сигнала, представленного в виде массива X(t). Правый IdP-тестер измеряет форму распределения выходного сигнала Y(t). Символом IdP[..] обозначена операция отображения тестером массива сигнала в особое, идентификационное число. Идентификационные числа Sx, Sy на выходах соответствующих тестеров сравниваются компаратором, выходной сигнал которого управляет работой дискретизатора. Максимально допустимое значение погрешности сравнения (Delta-доп) задается пользователем заранее. Дискретизатор постоянно увеличивает интервал дискретизации от 1 до некоторого максимального значения, при котором текущая разность (Delta S) между показаниями идентификационных тестеров не станет меньше Delta-доп.
Таким образом, предлагаемое устройство представляет собой систему автоматического регулирования интервала дискретизации в зависимости от формы входного сигнала. Достоинством подобного решения является то, что пользователю легче и удобнее задать значение допустимой погрешности сравнения. Это гарантирует ему адаптивность обработки сигналов произвольной формы и не надо гадать, можно ли для данного сигнала установить требуемый интервал дискретизации.
Рис. 1. Структурная схема модели устройства ЦОС
Информативными параметрами предлагаемого устройства являются: выборочная реализация выходного сигнала Y(t); фактор дискретизации (Resample Factor) и погрешность адекватности (Delta S = δ). Фактор дискретизации показывает, во сколько раз (по сравнению с 1) произошло увеличение интервала дискретизации. Погрешность адекватности (δ) показывает на сколько (в относительных единицах или %) форма сигнала на выходе отличается от формы сигнала на входе при наступлении условия идентификационной эквивалентности: Sx = Sy [1± δ].
Для сравнения с другими, подобными устройствами предлагается также использовать интегральный, комплексный показатель эффективности µ, равный отношению фактора дискретизации (R) и погрешности (δ,%) адекватности. В соответствие с этим показателем, тот алгоритм вторичной дискретизации лучше, у которого показатель эффективности больше. В свою очередь, эффективность больше тогда, когда фактор дискретизации больше, а погрешность адекватности – меньше.
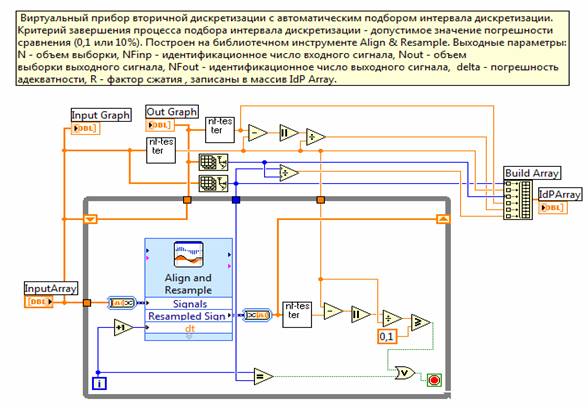
Рис. 2. Структура программного кода устройства ЦОС
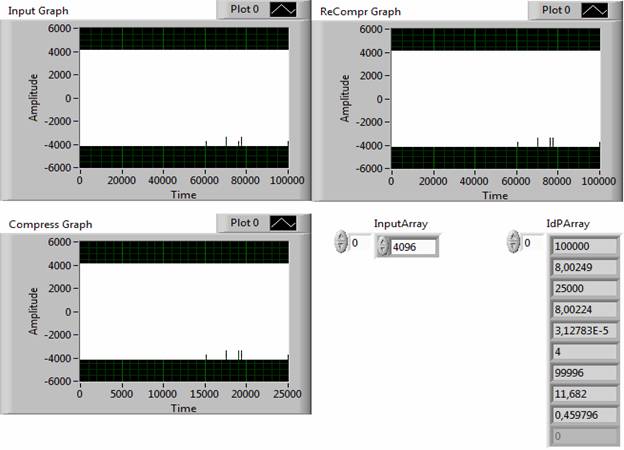
Алгоритм работы устройства ЦОС представлен в виде программного кода (рис. 2) виртуального прибора (ВП), выполненного в среде LabVIEW. Основу ВП составляют два идентификационных тестера NF-типа [4] и дискретизатор, построенный на библиотечном модуле Align & Resample.vi. Компаратор, осуществляющий сравнение идентификационных чисел входного и дискретизированного сигналов, построен на элементах вычитания и сравнения. С помощью переменной цикла While-Loop на входе дискретизатора формируется число, задающее текущее значение интервала дискретизации. Количественные параметры работы устройства: объем выборки (N) входного сигнала, идентификационное число (NFin) входного сигнала, объем выборки (Nout) выходного сигнала, идентификационное число (NFout) выходного сигнала, погрешность адекватности (δ) и фактор дискретизации (сжатия) выводятся в виде массива IdP Array.
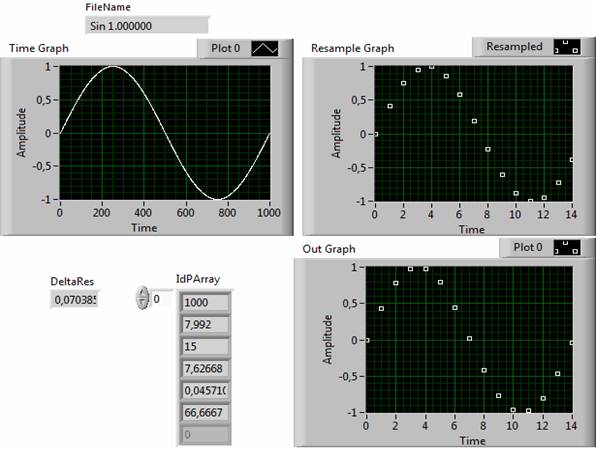
Рис. 3. Тестовый пример результатов работы типового и предлагаемого алгоритмов дискретизации
На рис. 3 представлены данные анализа тестового синусоидального сигнала (верхний, левый дисплей) с помощью типового метода вторичной дискретизации (правый верхний дисплей) и предлагаемого идентификационного метода (нижний дисплей). Полученные результаты (IdPArray) показывают, что при одинаковом количестве отсчетов (15) выходного сигнала, погрешность адекватности идентификационного метода (≈4,6%) примерно в 1,5 раза меньше погрешности адекватности (≈7%) типового метода.
Изучение особенностей идентификационного метода вторичной дискретизации проводилось по следующей программе. Во-первых, исследовалась возможность дискретизации и восстановления сигналов разных типов (периодические, случайные, фрактальные, модулированные, аддитивные смеси) и разной формы. Во-вторых, изучались свойства алгоритма при варьировании значения допустимой погрешности сравнения. В-третьих, оценивалось влияние дискретизации на спектр сигналов.
Правильность работы идентификационного алгоритма оценивалась визуально путем сравнения временных, вероятностных и спектральных функций входного и выходного сигналов. Достоверность результатов дискретизации оценивалась количественно измерениями погрешности адекватности.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
Некоторые особенности цифровой обработки сложных сигналов с помощью идентификационного алгоритма дискретизации представлены на рис. 4-8.
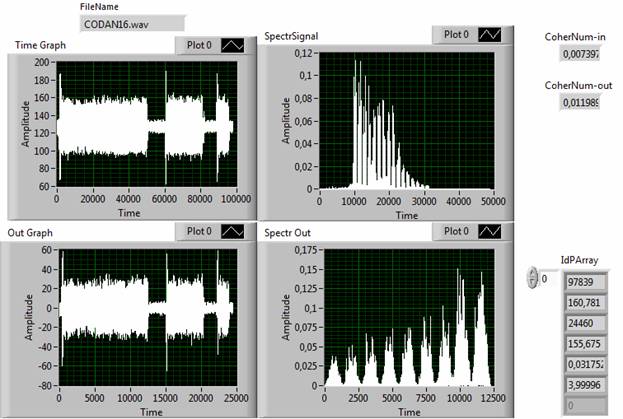
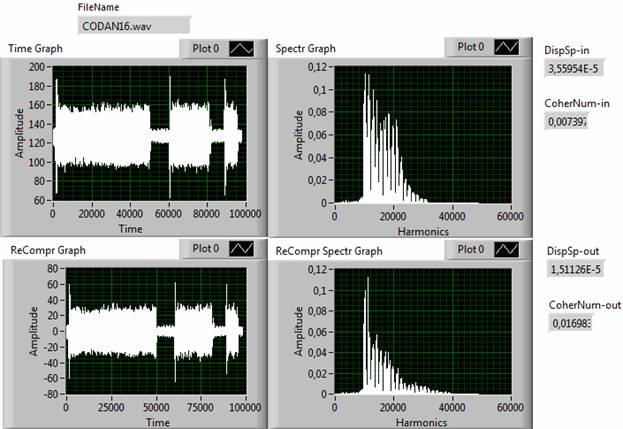
Рис. 4. Результат идентификационного преобразования временной и спектральной функции сигнала Cdn-16
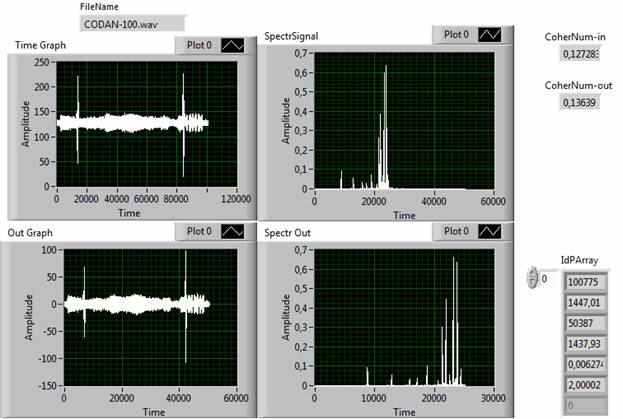
Рис. 5. Результат идентификационного преобразования временной и спектральной функции сигнала Cdn-100
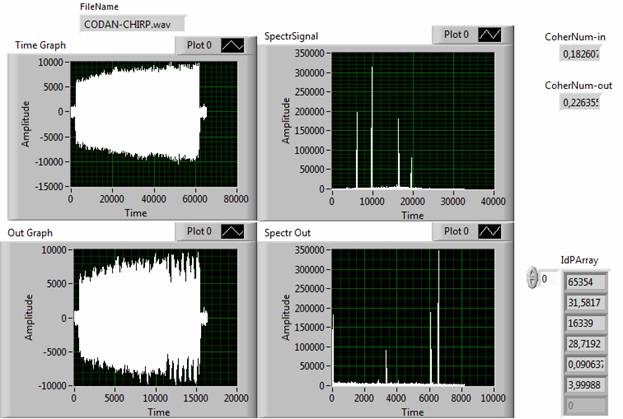
Рис. 6. Результат идентификационного преобразования временной и спектральной функции сигнала Cdn-Chirp
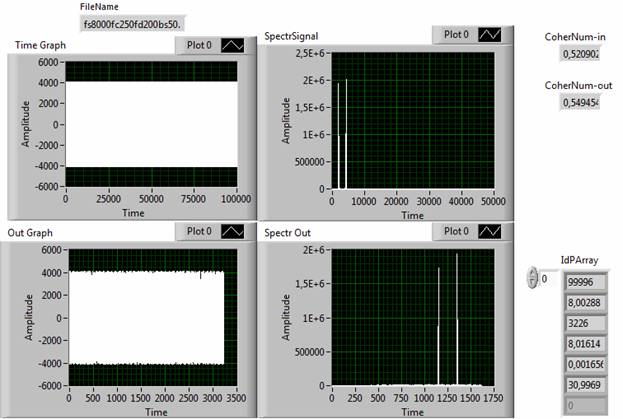
Рис. 7. Результат идентификационного преобразования временной и спектральной функции сигнала FC250
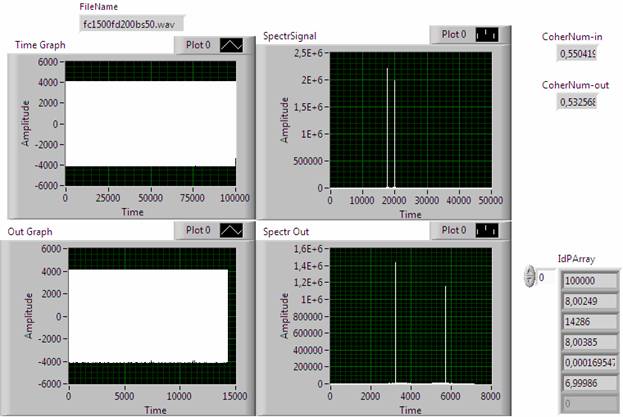
Рис. 8. Результат идентификационного преобразования временной и спектральной функции сигнала FC1500
Во-первых, как и ожидалось, увеличение интервала дискретизации и, следовательно, уменьшение частоты, позволяют реализовать компрессию временной функции сигналов. Для рассматриваемых примеров значение фактора сжатия составило от 2 (сигнал Cdn-100, рис. 5) до 31 (сигнал FC250, рис. 7). При этом погрешность адекватности во всех случаях не превысила 10%, что соответствует, установленному по умолчанию в инструменте (рис. 2), значению погрешности сравнения.
Во-вторых, уменьшение частоты дискретизации сдвигает спектр в низкочастотную область и подавляет гармоники, лежащие в высокочастотной области. Это полностью соответствует общетеоретическим соображениям.
В-третьих, для некоторых сигналов вторичная дискретизация приводила не к увеличению (рис. 4-7), а к уменьшению степени когерентности (рис. 8). Изучение этого эффекта требует проведения дополнительных исследований.
В-четвертых, наблюдается корреляция между свойством гладкости сигнала и степенью когерентности. В частности, чем более гладкой выглядит временная функция сигнала, тем выше его когерентность.
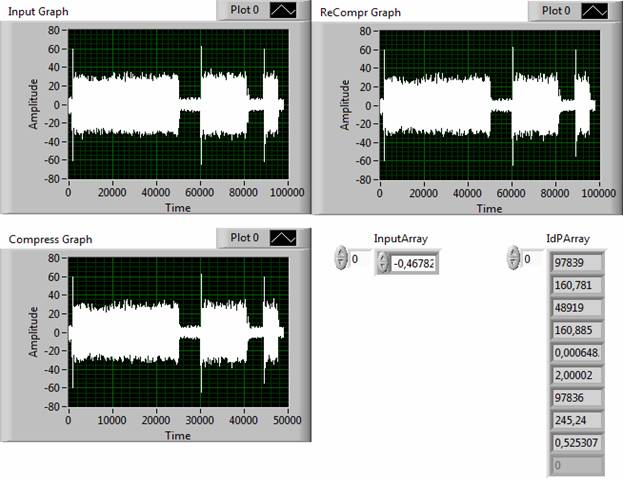
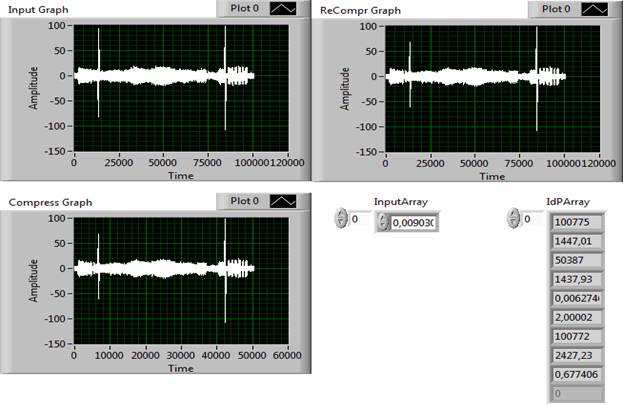
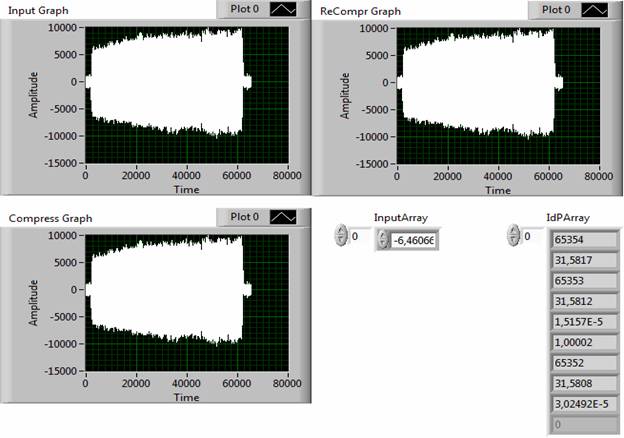
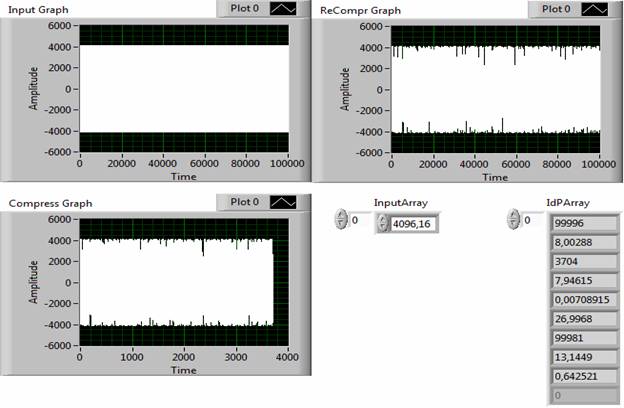
Особенности, связанные с восстановлением сложных сигналов отражены на рис. 9 – 13. Верхний ряд дисплеев отображает исходный и восстановленный сигналы, соответственно. Нижний дисплей визуализирует дискретизированный сигнал. В массиве IdP Array представлены результаты измерения параметров исходного, дискретизированного и восстановленного сигналов. В таблице представлены количественные результаты обработки простых типовых и сложных сигналов с учетом применения операций дискретизации и восстановления. В данном случае при дискретизации сигналов допустимое значение погрешности сравнения устанавливалось на уровне 1%. Указанные в таблице оценки погрешности преобразования относятся к относительной разности идентификационных чисел исходного и восстановленного сигналов.
Рис. 9. Результаты сжатия и восстановления сигнала Cdn-16
Рис. 10. Результаты сжатия и восстановления сигнала Cdn-100
Рис. 11. Результаты сжатия и восстановления сигнала Cdn-Chirp
Рис. 12. Результаты сжатия и восстановления сигнала FC250
Рис. 13. Результаты сжатия и восстановления сигнала FC1500
Таблица
Параметры операций сжатия-восстановления сигналов
|
№п/п |
Имя сигнала |
Параметры операций |
Примечание |
|
|
Фактор сжатия |
Погрешность преобразования,% |
|||
|
1 |
Sin-1 |
12 |
0,4 |
Группа простых сигналов, N=1000, F=1 |
|
2 |
Cos-1 |
10 |
1 |
|
|
3 |
Tri-1 |
3 |
0,8 |
|
|
4 |
Squ-1 |
11 |
0,8 |
|
|
5 |
Saw-1 |
4 |
0,25 |
|
|
6 |
Cdn-16 |
2 |
53 |
Группа сложных сигналов разной структуры |
|
7 |
Cdn-100 |
2 |
68 |
|
|
8 |
Cdn-Chirp |
1 |
0,003 |
|
|
9 |
Fc250 |
27 |
64 |
Группа сигналов одинаковой структуры |
|
10 |
Fc1500 |
4 |
46 |
|
В группе простых сигналов погрешность преобразования в цепочке исходный – восстановленный сигнал не превысила, заданную по умолчанию погрешность сравнения дискретизатора (1%).
В группе сложных сигналов только сигнал с именем Cdn-Chirp был преобразован с малой погрешностью (0,003%) в силу того, что с помощью предлагаемого алгоритма его сжать не удалось (фактор сжатия = 1). Это обстоятельство, по-видимому, указывает на то, что сигнал Cdn-Chirp при Delta-доп = 1% не имеет информационной избыточности.
Рис. 14. Временные и спектральные функции исходного и восстановленного сигнала Cdn-16
Ряд сигналов был преобразован с большой погрешностью (от 46% до 68%). Однако, визуально, каких-либо существенных искажений временных функций у этих сигналов не наблюдается. Можно предположить, что погрешность преобразования, на самом деле, характеризует искажения не временной, а спектральной функции восстановленного сигнала. В подтверждение этому, на рис. 14 представлены временные и спектральные функции исходного и восстановленного сигнала Cdn-16, а также измеренные значения дисперсий и степени когерентности обоих спектров. Если рассчитать относительную разность дисперсий (α = [Din – Dout]/Din), то получится значение (58%), примерно равное погрешности преобразования (53%). Таким образом, малым искажениям сложных сигналов во временной области могут соответствовать большие изменения спектральной характеристики, но всегда в сторону уменьшения эффективной ширины спектра.
ВЫВОДЫ
Проведенные исследования показали, что, во-первых, идентификационный метод вторичной дискретизации является более эффективным по сравнению с известными методами. В частности, при одинаковом факторе дискретизации получается меньшая погрешность адекватности. Во-вторых, применение идентификационного метода не требует от пользователя знаний о форме сигнала, поскольку является адаптивным к этому свойству. В-третьих, идентификационный метод может быть использован для построения определенного класса архиваторов, которые не требуют выполнения операции восстановления в силу того, сжатие исходного сигнала произведено с установленной пользователем, допустимой погрешностью. Другими словами, идентификационный метод просто удаляет из сигнала неинформативные компоненты, не затрагивая наиболее существенные особенности формы распределения мгновенных значений. В-четвертых, с помощью предлагаемого метода можно решать задачи фильтрации, поскольку наиболее существенные изменения наблюдаются именно в спектральной области.
ЛИТЕРАТУРА
1. Басараб М.А. Цифровая обработка сигналов на основе теоремы Уиттекера-Котельникова-Шеннона. – М.: Радиотехника, 2004. – 72 с.
2. Цыганенко В.Н., Белик А.Г. Дискретизация измерительных сигналов на основе прикладных функциональных моделей //Цифровая обработка сигналов. – М.: 2009. - №2. – С.58-60.
3. Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: Монография. – Омск: Изд-во ОмГТУ, 2010. – 216 с.
4. Кликушин Ю.Н. Классификационные шкалы для распределений вероятности.// Интернет-статья. - М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2000 г.: http://jre.cplire.ru