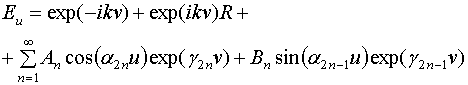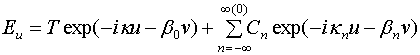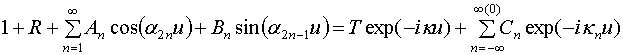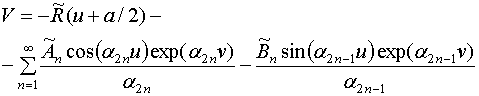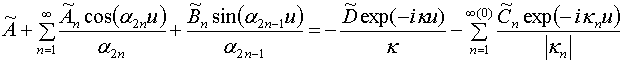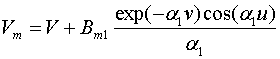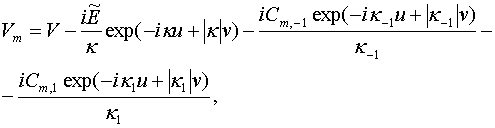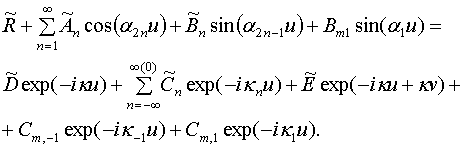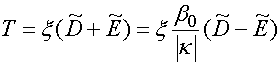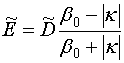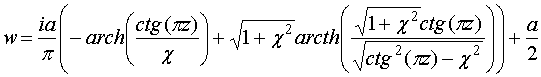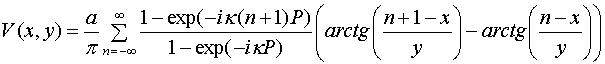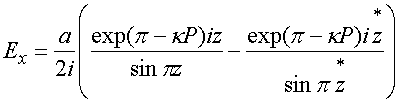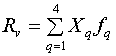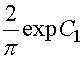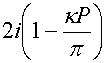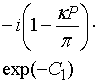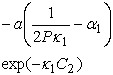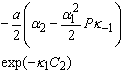УДК 621.396.67
КВАЗИСТАТИЧЕСКИЙ АНАЛИЗ БЕСКОНЕЧНОЙ РЕШЕТКИ ИЗ МЕТАЛЛИЧЕСКИХ ПЛАСТИН КОНЕЧНОЙ ТОЛЩИНЫ
С. Е. Банков 1, В. Н. Козин 2
1 ИРЭ им. В.А. Котельникова РАН, 2 НИУ МЭИ
Получена 20 февраля 2013 г.
Аннотация. Рассмотрена задача об излучении электромагнитных волн из решетки полубесконечных плоских волноводов, образованных металлическими пластинами конечной толщины. Решение в аналитическом виде получено квазистатическим методом конформного отображения с учетом конечного числа динамических поправок, позволяющих описывать такие эффекты, как возбуждение гармоник Флоке высших порядков. Приведены результаты сравнения предложенного решения с известными результатами, полученными методом Винера-Хопфа.
Ключевые слова: решетка, плоский волновод, конформное отображение.
Abstract. A problem of electromagnetic wave radiation from an array of semi infinite parallel plate waveguides formed by metal plates with a finite thickness is considered. Solution in analytic form is obtained by quasi-static method of conformal mapping. The solution contains dynamical terms that take into account such effects like radiation of high order Floquet harmonics. Numerical results are compared with known results obtained by Viener-Hopf’s technique.
Keywords: array, parallel plate waveguide, conformal mapping.
1. Введение
Структура, показанная на рис. 1, неоднократно рассматривалась разными авторами [1-3]. Результаты ее анализа часто используются в качестве эталона для проверки истинности общих алгоритмов в предельных ситуациях. Кроме того, решение электродинамической задачи для решетки из плоских толстостенных металлических волноводов представляет и самостоятельный интерес с точки зрения использования его в качестве ключевого результата для расчета более сложных структур.
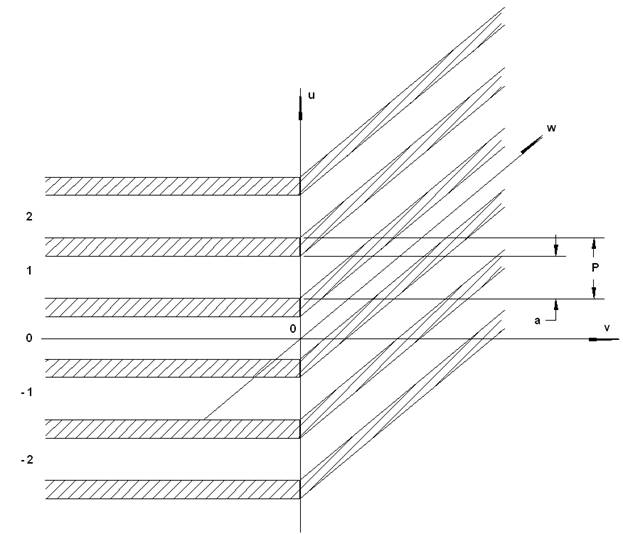
Рис. 1. Решетка металлических пластин конечной толщины
В данной работе предлагается новый подход к решению соответствующей граничной задачи, позволяющий указать простой и эффективный алгоритм для численных расчетов. Этот подход является квазистатическим и похож на метод использованный в ходе анализа Е - плоскостной ступеньки в металлическом волноводе с помощью конформных отображений [4].
Прежде чем непосредственно
перейти к математическим преобразованиям, кратко опишем основные этапы решения
граничной задачи. Первый шаг состоит в записи представлений для полей по обе
стороны от границы решетки. В одном полупространстве нами использовалось
разложение по модам плоского волновода, а в другом по гармоникам Флоке. Такие
разложения записываются как для волнового уравнения, так и для уравнения
Лапласа, то есть статического решения. Показывается, что для всех членов
разложений, кроме нескольких слагаемых с низшими индексами оба представления
поля эквивалентны. Чтобы эквивалентность была полной в статическое решение
вводятся дополнительные слагаемые, число которых совпадает с числом
неэквивалентных членов разложений ![]() Далее, дополненное
статическое решение ищется в явном виде с помощью конформного отображения
области решетки на верхнюю полуплоскость. Получаемое решение содержит ряд
неизвестных констант, для которых записывается система линейных алгебраических
уравнений размерностью
Далее, дополненное
статическое решение ищется в явном виде с помощью конформного отображения
области решетки на верхнюю полуплоскость. Получаемое решение содержит ряд
неизвестных констант, для которых записывается система линейных алгебраических
уравнений размерностью ![]() . Ее решение позволяет
окончательно найти все характеристики решетки
. Ее решение позволяет
окончательно найти все характеристики решетки
В данной статье
рассматривается случай ![]() , соответствующий введению
динамических поправок для двух волноводных мод нулевого и первого порядков и
трех гармоник Флоке: нулевой, первой и минус первой. Численные расчеты
показали, что такое приближение хорошо описывает не только преобразование
основных пространственных гармоник, но и их трансформацию в волны ближайших
порядков.
, соответствующий введению
динамических поправок для двух волноводных мод нулевого и первого порядков и
трех гармоник Флоке: нулевой, первой и минус первой. Численные расчеты
показали, что такое приближение хорошо описывает не только преобразование
основных пространственных гармоник, но и их трансформацию в волны ближайших
порядков.
2. Модовые представления полей
Будем рассматривать
решетку, возбуждаемую волнами металлических волноводов, набегающими из
отрицательного полупространства при ![]() < 0. При этом
предполагается, что поля в каждом канале отличаются друг от друга только
фазовыми множителями типа
< 0. При этом
предполагается, что поля в каждом канале отличаются друг от друга только
фазовыми множителями типа ![]() , где k - константа,
задающая фазовый сдвиг, m - номер канала, Р - период решетки. Таким образом, мы имеем
дело с квазипериодическими решениями, которые могут быть интерпретированы как
обобщенные плоские волны.
, где k - константа,
задающая фазовый сдвиг, m - номер канала, Р - период решетки. Таким образом, мы имеем
дело с квазипериодическими решениями, которые могут быть интерпретированы как
обобщенные плоские волны.
Будем рассматривать
возбуждение решетки основными Т – волнами волноводов, распространяющимися в
плоскости  вдоль оси
вдоль оси 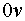 .
.
Запишем, удовлетворяющие
волновому уравнению компоненты электромагнитного поля при 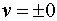 следующим образом:
следующим образом:
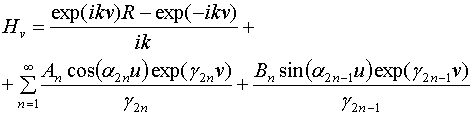 ,
, ![]() ,
,
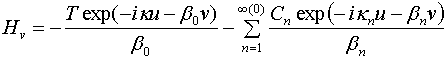 ,
, ![]() ,
,
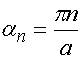 ,
, 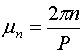 ,
, 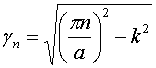 ,
,
![]()
![]() ,
,
где 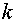 - волновое число
свободного пространства.
- волновое число
свободного пространства.
Формулы (1) записаны для
поля в металлическом волноводе при ![]() , R и T - коэффициенты отражения и передачи по электрическому
полю,
, R и T - коэффициенты отражения и передачи по электрическому
полю, ![]() - амплитуды собственных волн волновода,
которые возбуждаются в плоскости
- амплитуды собственных волн волновода,
которые возбуждаются в плоскости ![]() ,
, ![]() - амплитуды гармоник Флоке, которые
описывают поле в свободном пространстве. Символ (0), встречающийся в формулах
(2), означает, что суммирование ведется по всем индексам кроме нулевого.
- амплитуды гармоник Флоке, которые
описывают поле в свободном пространстве. Символ (0), встречающийся в формулах
(2), означает, что суммирование ведется по всем индексам кроме нулевого.
При ![]() должны
соблюдаться условия непрерывности тангенциальных компонент поля. Удовлетворение
этим условиям приводит к следующим двум равенствам:
должны
соблюдаться условия непрерывности тангенциальных компонент поля. Удовлетворение
этим условиям приводит к следующим двум равенствам:
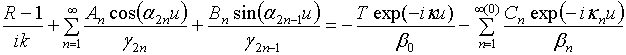 .
.
Аналогичные
уравнения могут быть получены для статических полей, являющихся решением
уравнения Лапласа. Статическое электрическое поле удобно выражается через
комплексный потенциал ![]() :
:
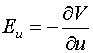 ,
, 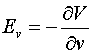 . (4)
. (4)
Статическое поле
характеризуется также силовой функцией ![]() ,
которая связана с комплексным потенциалом условиями Коши - Римана:
,
которая связана с комплексным потенциалом условиями Коши - Римана:
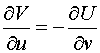 . (5)
. (5)
Для функций ![]() и
и ![]() справедлива
следующая запись:
справедлива
следующая запись:
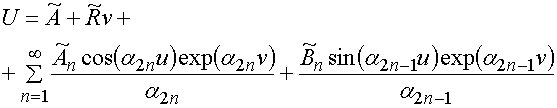 ,
, ![]()
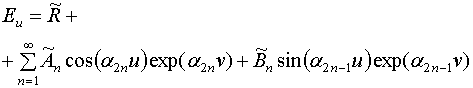 ,
, ![]() (7)
(7)
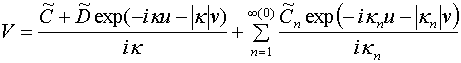 , (8)
, (8)
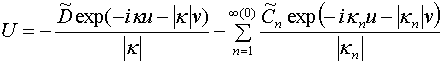 ,
, ![]() ,
,
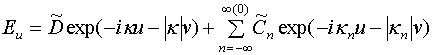 ,
, ![]() , (9)
, (9)
Выражения (6)
- (9) записаны для периода решетки, расположенного в начале координат (m = 0). Постоянные ![]() имеют смысл коэффициентов разложения
статического поля в области волноводного канала. Аналогично постоянные
имеют смысл коэффициентов разложения
статического поля в области волноводного канала. Аналогично постоянные ![]() являются коэффициентами разложения
статического поля в свободном пространстве по гармоникам Флоке. При v = 0 функции
являются коэффициентами разложения
статического поля в свободном пространстве по гармоникам Флоке. При v = 0 функции ![]() и
и ![]() должны быть непрерывны:
должны быть непрерывны:
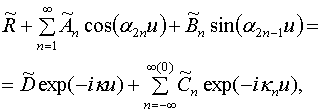 (10)
(10)
Сравнивая равенства (3) с соотношениями (10), (11) легко увидеть, что они могут быть тождественны друг другу, при выполнении следующих соотношений:
Однако эти
соотношения строго выполняются только асимптотически при ![]() . На практике при типовых значениях
высоты волновода а, соответствующих одноволновому режиму и периоду
решетки Р порядка (0.6 - 0.8)l,
. На практике при типовых значениях
высоты волновода а, соответствующих одноволновому режиму и периоду
решетки Р порядка (0.6 - 0.8)l, ![]() -
длина волны в свободном пространстве, равенства (12) справедливы для всех n, кроме n = 0, 1 в случае
постоянных
-
длина волны в свободном пространстве, равенства (12) справедливы для всех n, кроме n = 0, 1 в случае
постоянных ![]() и n = -1, 0, 1 в случае
постоянных
и n = -1, 0, 1 в случае
постоянных ![]() . Таким образом, достаточно строго учесть вклад
основной волны и первого высшего типа металлического волновода, а также
нулевой, первой и минус первой гармоник Флоке в свободном пространстве.
Остальные члены электродинамического представления поля могут быть заменены
статическими решениями.
. Таким образом, достаточно строго учесть вклад
основной волны и первого высшего типа металлического волновода, а также
нулевой, первой и минус первой гармоник Флоке в свободном пространстве.
Остальные члены электродинамического представления поля могут быть заменены
статическими решениями.
3. Дополненное решение уравнения Лапласа
Для того, чтобы
равенства (10), (11) совпадали с (3) надо добавить в выражения для функций ![]() дополнительные слагаемые, которые также
должны удовлетворять уравнению Лапласа, граничным условиям и условиям
периодичности и, в тоже время не должны совпадать с уже записанными выше
членами разложений. Всем этим условиям удовлетворяют функции, полностью
совпадающие с членами рядов (6) - (9) за исключением того, что они растут при
дополнительные слагаемые, которые также
должны удовлетворять уравнению Лапласа, граничным условиям и условиям
периодичности и, в тоже время не должны совпадать с уже записанными выше
членами разложений. Всем этим условиям удовлетворяют функции, полностью
совпадающие с членами рядов (6) - (9) за исключением того, что они растут при ![]() . Запишем получаемые после их добавления
функции
. Запишем получаемые после их добавления
функции ![]() :
:
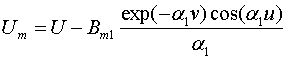 ,
, ![]() ,
(13)
,
(13)
![]() ,
, ![]() ,
,
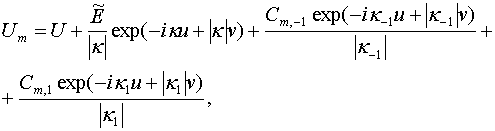
![]() , (14)
, (14)
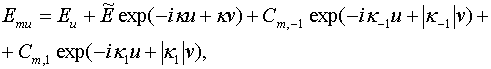 ,
, ![]() ,
,
Подставим далее выражения
(13) и (14) в граничные условия непрерывности функций ![]() и
и
![]() при
при ![]() и
получим два соотношения аналогичных уравнениям (11) и (12):
и
получим два соотношения аналогичных уравнениям (11) и (12):
(15)
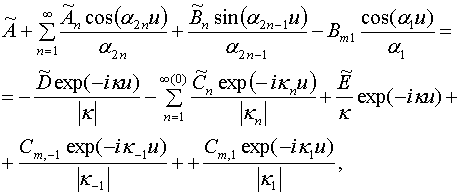
Установим следующие соотношения между коэффициентами, входящими в статические и электродинамические представления поля:
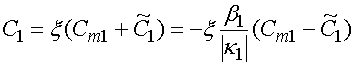 ,
,
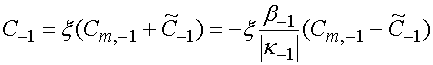 , (16)
, (16)
![]() ,
,
![]() ,
,
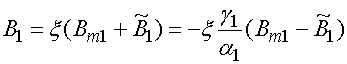 .
.
В формулах (15) ![]() - неизвестная
произвольная постоянная. Если наряду с соотношениями (15) дополнительно
положить, что
- неизвестная
произвольная постоянная. Если наряду с соотношениями (15) дополнительно
положить, что
![]() ,
, ![]() ,
, ![]() ,
,
то статические уравнения (15) оказываются полностью эквивалентными электродинамической системе уравнений (3).
Из равенств (16) можно получить следующие соотношения:
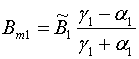 , (17)
, (17)
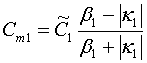 ,
,
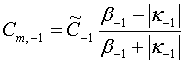 .
.
Теперь наша задача состоит в том, чтобы найти статическое поле в решетке, имеющее соответствующее поведение на бесконечности.
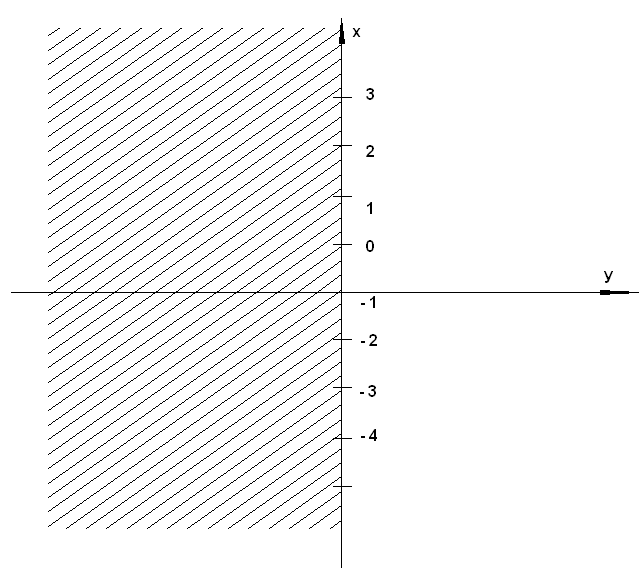
Рис. 2. Отображение решетки на плоскость ![]()
Для ее
решения отобразим верхнюю полуплоскость плоскости комплексной переменной ![]() (см. рис. 2) на внутренность фигуры в
плоскости
(см. рис. 2) на внутренность фигуры в
плоскости ![]() . Такое отображение можно получить с
помощью интеграла Кристофеля - Шварца [5]. Мы не будем подробно описывать
технику интегрирования, а приведем окончательный результат:
. Такое отображение можно получить с
помощью интеграла Кристофеля - Шварца [5]. Мы не будем подробно описывать
технику интегрирования, а приведем окончательный результат:
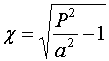 . (18)
. (18)
Преобразование
(18) отображает границу каждой металлической пластины в плоскости ![]() на отрезок действительной оси на
плоскости
на отрезок действительной оси на
плоскости ![]() . Поскольку потенциал на металлической
поверхности не меняется в силу свойств статического поля, то функция
. Поскольку потенциал на металлической
поверхности не меняется в силу свойств статического поля, то функция ![]() , описывающая потенциал на оси 0х известна:
, описывающая потенциал на оси 0х известна:
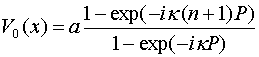 ,
,
![]() ,
, ![]() (19)
(19)
Нам необходимо найти потенциал во всем полупространстве. Для этого можно воспользоваться готовым решением из [5]:
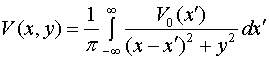 . (20)
. (20)
Заменим в выражении (20) интеграл в бесконечных пределах на сумму интегралов в ограниченных интервалах, используя выражение (19). В результате имеем для потенциала представление в виде бесконечной суммы:
Ряд в (21)
аналитически не суммируется, однако в случае его производной по х такое
суммирование возможно. Таким образом, для компоненты электрического поля ![]() и силовой функции
и силовой функции ![]() имеем
следующие формулы:
имеем
следующие формулы:
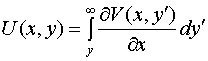 . (22),
. (22),
Рассмотрим поведение
функций ![]() и
и ![]() при
при ![]() .
Легко убедиться, что они ведут себя следующим образом:
.
Легко убедиться, что они ведут себя следующим образом:
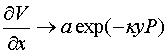 ,
, 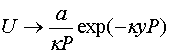 . (23)
. (23)
Кроме того из выражения (17) видно, что при больших у выполняется равенство:
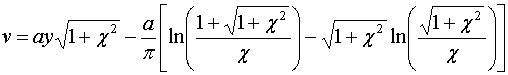 .
.
Таким
образом, координата ![]() растет при
растет при ![]() пропорционально
пропорционально ![]() . Отсюда получаем, что функции
. Отсюда получаем, что функции ![]() и
и ![]() ведут
себя как
ведут
себя как ![]() . Такого результата следовало ожидать, так
как формула (21) дает решение ограниченное на бесконечности. В тоже время нам
требуется решение растущее на бесконечности. Чтобы получить его следует
добавить к (21) соответствующие слагаемые, которые должны удовлетворять
уравнению Лапласа, условию периодичности и не должны изменять потенциал при у
= 0. Вообще говоря, подобная процедура уже была продемонстрирована выше в
третьем разделе. Однако, там она была проделана на плоскости переменной w, в то время как сейчас
нам это надо сделать уже на плоскости z, поскольку в явном виде
решение для потенциала нам известно, как раз именно на плоскости z. Отличие последнего
случая достаточно существенное, так как вид требуемых слагаемых на плоскости z не столь очевиден как на
плоскости w. Особо это справедливо для слагаемых корректирующих поведение
потенциала при
. Такого результата следовало ожидать, так
как формула (21) дает решение ограниченное на бесконечности. В тоже время нам
требуется решение растущее на бесконечности. Чтобы получить его следует
добавить к (21) соответствующие слагаемые, которые должны удовлетворять
уравнению Лапласа, условию периодичности и не должны изменять потенциал при у
= 0. Вообще говоря, подобная процедура уже была продемонстрирована выше в
третьем разделе. Однако, там она была проделана на плоскости переменной w, в то время как сейчас
нам это надо сделать уже на плоскости z, поскольку в явном виде
решение для потенциала нам известно, как раз именно на плоскости z. Отличие последнего
случая достаточно существенное, так как вид требуемых слагаемых на плоскости z не столь очевиден как на
плоскости w. Особо это справедливо для слагаемых корректирующих поведение
потенциала при ![]() . Введем функцию
. Введем функцию ![]() следующим образом:
следующим образом:
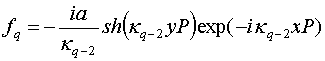 ,
, ![]() ,
,
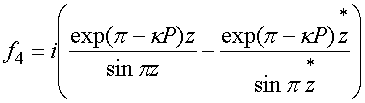 .
.
Здесь ![]() - неизвестные постоянные. Можно
убедиться, что компоненты суммы в (24) представляют собой как раз те самые
упомянутые выше слагаемые, корректирующие выражение для потенциала
- неизвестные постоянные. Можно
убедиться, что компоненты суммы в (24) представляют собой как раз те самые
упомянутые выше слагаемые, корректирующие выражение для потенциала ![]() . Причем первые три слагаемые осуществляют
коррекцию в положительной полуплоскости, а четвертое в отрицательной. Используя
условия Коши-Римана, можно получить выражение для функции корректирующей
. Причем первые три слагаемые осуществляют
коррекцию в положительной полуплоскости, а четвертое в отрицательной. Используя
условия Коши-Римана, можно получить выражение для функции корректирующей ![]() :
:
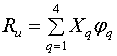 , (25)
, (25)
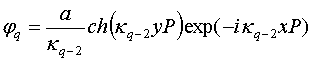 ,
, ![]() ,
,
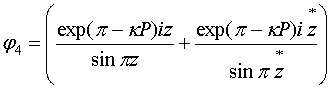 .
.
Добавим функции ![]() к выражениям (21) и (22), описывающим
решение на плоскости
к выражениям (21) и (22), описывающим
решение на плоскости ![]() , убывающее на бесконечности, и
получим функции
, убывающее на бесконечности, и
получим функции ![]() , описывающее дополненное
решение уравнения Лапласа на плоскости
, описывающее дополненное
решение уравнения Лапласа на плоскости ![]() растущее
на бесконечности:
растущее
на бесконечности:
![]() .
.
Отметим, что
выражения (26) описывают поведение потенциала и силовой функции на плоскости z. Чтобы найти неизвестные
коэффициенты ![]() следует
совершить обратный переход на плоскость w, который позволит
установить связи между
следует
совершить обратный переход на плоскость w, который позволит
установить связи между ![]() и введенными
ранее коэффициентами
и введенными
ранее коэффициентами ![]() и т.д. Выразив их через
и т.д. Выразив их через ![]() , мы можем
подставить полученные формулы в четыре уравнения (17) и получить систему
линейных уравнений относительно неизвестных
, мы можем
подставить полученные формулы в четыре уравнения (17) и получить систему
линейных уравнений относительно неизвестных ![]() , решив которую мы найдем интересующие нас коэффициенты. К
сожалению, обратный переход на плоскость w совершить затруднительно
по той причине, что в явном виде нам известна только зависимость w(z). Получить аналитическое
выражение для обратной функции z(w) не представляется возможным. Выход из такого
положения в том, что нам нет необходимости знать аналитическое выражение для
потенциала на всей плоскости w, а достаточно только определить его
асимптотическое поведение на бесконечности в соответствующих полуплоскостях.
Дело в том, что слагаемые пропорциональные коэффициентам
, решив которую мы найдем интересующие нас коэффициенты. К
сожалению, обратный переход на плоскость w совершить затруднительно
по той причине, что в явном виде нам известна только зависимость w(z). Получить аналитическое
выражение для обратной функции z(w) не представляется возможным. Выход из такого
положения в том, что нам нет необходимости знать аналитическое выражение для
потенциала на всей плоскости w, а достаточно только определить его
асимптотическое поведение на бесконечности в соответствующих полуплоскостях.
Дело в том, что слагаемые пропорциональные коэффициентам ![]() и т.д. являются доминирующими, когда çv 箥 и, следовательно,
сравнивая разложения (6), (7), (14) с асимптотическими разложениями для
и т.д. являются доминирующими, когда çv 箥 и, следовательно,
сравнивая разложения (6), (7), (14) с асимптотическими разложениями для ![]() (24) –
(26) мы можем получить искомую связь между
неизвестными коэффициентами. Отметим также, что в предельной ситуации, когда çv 箥 обратить функцию w(z) уже возможно.
(24) –
(26) мы можем получить искомую связь между
неизвестными коэффициентами. Отметим также, что в предельной ситуации, когда çv 箥 обратить функцию w(z) уже возможно.
Представим
функции ![]() при v ®¥, u = 0 в виде следующих асимптотических разложений:
при v ®¥, u = 0 в виде следующих асимптотических разложений:
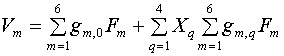 , (27)
, (27)
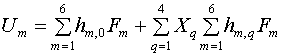 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Здесь ![]() - коэффициенты асимптотического
разложения функции
- коэффициенты асимптотического
разложения функции ![]() , а
, а ![]() -
коэффициенты асимптотических разложений функций
-
коэффициенты асимптотических разложений функций ![]() .
Аналогично
.
Аналогично ![]() - коэффициенты разложения для функции
- коэффициенты разложения для функции ![]() , а
, а ![]() -
коэффициенты разложений функций
-
коэффициенты разложений функций ![]() . В формулах (27)
удержано шесть главных членов разложений, что совпадает с числом неизвестных
коэффициентов
. В формулах (27)
удержано шесть главных членов разложений, что совпадает с числом неизвестных
коэффициентов ![]() ,
, ![]() ,
описывающих в старших порядках поведение разложений (14) на бесконечности.
Целесообразно ввести следующие обозначения:
,
описывающих в старших порядках поведение разложений (14) на бесконечности.
Целесообразно ввести следующие обозначения:
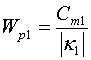 ,
, 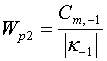 ,
, 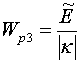 , (28)
, (28)
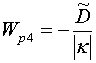 ,
, 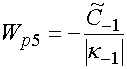 ,
,
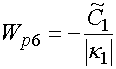 .
.
С их помощью
мы можем записать асимптотическое представление для функции ![]() (14) при
(14) при ![]() :
:
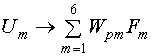 . (29)
. (29)
Сравним его с
представлением (27) и приравняем коэффициенты при функциях ![]() :
:
Соотношения
(30) выражают шесть неизвестных ![]() через параметры
через параметры ![]() . В уравнения (17) наряду с
. В уравнения (17) наряду с ![]() входит ряд параметров, которые
определяются асимптотическим поведением решения при
входит ряд параметров, которые
определяются асимптотическим поведением решения при ![]() . Чтобы
найти их нам нужно рассмотреть поведение функций
. Чтобы
найти их нам нужно рассмотреть поведение функций ![]() при
при ![]() .
.
Представим решение (26) в следующем виде:
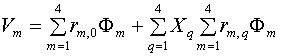 , (31)
, (31)
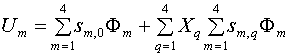 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
где ![]() - коэффициенты асимптотического
разложения функции
- коэффициенты асимптотического
разложения функции ![]() (26) при
(26) при ![]() , а
, а ![]() - коэффициенты асимптотических
разложений функций
- коэффициенты асимптотических
разложений функций ![]() при
при ![]() ,
, ![]() -
коэффициенты разложения функции
-
коэффициенты разложения функции ![]() , а
, а ![]() функций
функций ![]() .
.
Асимптотики
функций ![]() ,
,![]() (26)
при
(26)
при ![]() необходимо искать с учетом поведения
конформного отображения (18). С его помощью можно получить, что при
необходимо искать с учетом поведения
конформного отображения (18). С его помощью можно получить, что при ![]() переменная
переменная ![]() пропорциональна
функции
пропорциональна
функции ![]() , которая стремится к нулю при
, которая стремится к нулю при ![]() .
.
Рассмотрим теперь
поведение функций ![]() ,
,![]() (13) при
(13) при ![]() . Введем
далее следующие обозначения:
. Введем
далее следующие обозначения:
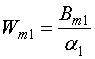 ,
,
![]() ,
, ![]() ,
, 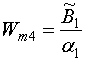 . (32)
. (32)
Соотношения (32) вместе с
выражениями (13) позволяют записать для функции ![]() асимптотическое разложение при
асимптотическое разложение при ![]() :
:
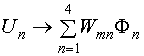 . (33)
. (33)
Сравнивая
выражения (33) и (31), находим соотношения для параметров ![]() :
:
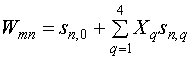 ,
, ![]() , (34)
, (34)
Формулы (30)
и (34) полностью определяют постоянные из решения в плоскости ![]() через четыре коэффициента
через четыре коэффициента ![]() . Подставим далее равенства (30) и (34) в
уравнения (17) и получим систему линейных алгебраических уравнений относительно
коэффициентов
. Подставим далее равенства (30) и (34) в
уравнения (17) и получим систему линейных алгебраических уравнений относительно
коэффициентов ![]() :
:
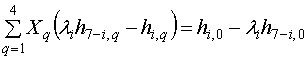 ,
, ![]() , (35)
, (35)
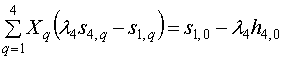 ,
,
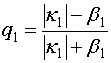 ,
, 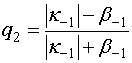 ,
, 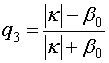 ,
, 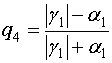 .
.
Из
соотношений (16) получаем полезное выражение для входной проводимости решетки ![]() :
:
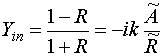 , (36)
, (36)
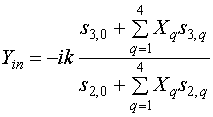 . (37)
. (37)
4. Вычисление коэффициентов асимптотических разложений
Для того,
чтобы получить численные результаты необходимо знание коэффициентов асимптотических
разложений: ![]() и
и ![]() . Их
определение требует достаточно громоздких и трудоемких математических
преобразований. Поясним их на примере вычисления коэффициентов
. Их
определение требует достаточно громоздких и трудоемких математических
преобразований. Поясним их на примере вычисления коэффициентов ![]() .
.
На первом этапе
найдем асимптотическое выражение для координаты ![]() при
при ![]() ,
, ![]() .
Отметим, что стремление координаты
.
Отметим, что стремление координаты ![]() к нулю обеспечивает
стремление точки на плоскости
к нулю обеспечивает
стремление точки на плоскости ![]() к минус бесконечности
вдоль оси
к минус бесконечности
вдоль оси ![]() . Данная задача решается с помощью
соотношения (18). Можно показать, что в окрестности точки
. Данная задача решается с помощью
соотношения (18). Можно показать, что в окрестности точки ![]() функция
функция ![]() может
быть представлена в виде разложения:
может
быть представлена в виде разложения:
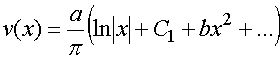 , (38)
, (38)
где ![]() и
и ![]() постоянные,
определяемые соотношениями:
постоянные,
определяемые соотношениями:
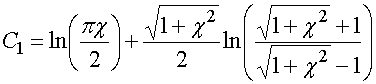 , (39)
, (39)
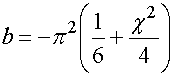 .
.
Нам необходимо
вместо разложения ![]() получить разложение вида
получить разложение вида ![]() . Обратить выражение (38) можно асимптотически,
представляя функцию
. Обратить выражение (38) можно асимптотически,
представляя функцию ![]() в виде ряда:
в виде ряда:
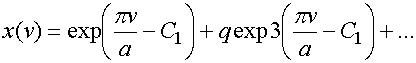 , (40)
, (40)
Подставим
соотношение (40) в формулу (38) и приравняем коэффициенты при одинаковых
экспоненциальных слагаемых. В результате находим выражение для коэффициента ![]() :
:
![]() . (41)
. (41)
На следующем
этапе мы должны подставить соотношение (40) в функции ![]() и
представить в виде асимптотических разложений:
и
представить в виде асимптотических разложений:
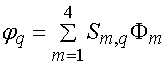 . (42)
. (42)
Найденные таким образом
коэффициенты ![]() совпадают с искомыми коэффициентами
совпадают с искомыми коэффициентами ![]() . Они приведены в табл. 1.
. Они приведены в табл. 1.
Табл. 1. Коэффициенты
асимптотических разложений при ![]() .
.
|
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Номер столбца таблицы
соответствует индексу ![]() , а строки индексу
, а строки индексу ![]() . Коэффициент
. Коэффициент ![]() требует
отдельного анализа. Для него получено следующее соотношение:
требует
отдельного анализа. Для него получено следующее соотношение:
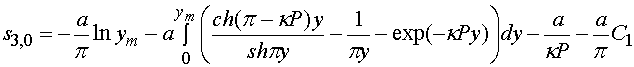 , (43)
, (43)
где ![]() - параметр, выбираемый из условия
- параметр, выбираемый из условия ![]() .
.
Коэффициенты
асимптотических разложений ![]() при
при ![]() также ищутся по схеме описанной выше. Они
приведены в табл. 2.
также ищутся по схеме описанной выше. Они
приведены в табл. 2.
Табл. 2. Коэффициенты
асимптотических разложений при ![]() .
.
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Интеграл в
формуле (43) аналитически не вычисляется. Однако для него была найдена простая
аппроксимация. С ее помощью можно записать приближенное выражение для
коэффициента ![]() , которое выполняется с относительной
погрешностью не превышающей 2.5%:
, которое выполняется с относительной
погрешностью не превышающей 2.5%:
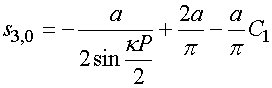 . (44)
. (44)
Постоянная ![]() , присутствующая в табл. 2 выражается
следующим образом:
, присутствующая в табл. 2 выражается
следующим образом:
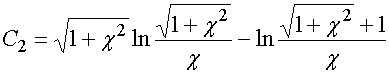 . (45)
. (45)
5. Численные результаты
Для проверки предложенного
алгоритма расчета решетки были произведены расчеты модуля и фазы коэффициента
отражения R как функции параметра ![]() , выраженного в градусах. При этом
величина k равна
, выраженного в градусах. При этом
величина k равна ![]() , где q это угол под которым нулевая гармоника Флоке
излучается из решетки. Этот угол отсчитывается от нормали к плоскости решетки.
Расчеты проводились и для случая бесконечно тонких стенок металлических
волноводов, поскольку для него известно строгое решение, полученной методом
Винера - Хопфа [6]. Результаты расчетов представлены на рис. 3-6. Пунктирными
линиями показаны графики, соответствующие расчету по методу Винера - Хопфа.
, где q это угол под которым нулевая гармоника Флоке
излучается из решетки. Этот угол отсчитывается от нормали к плоскости решетки.
Расчеты проводились и для случая бесконечно тонких стенок металлических
волноводов, поскольку для него известно строгое решение, полученной методом
Винера - Хопфа [6]. Результаты расчетов представлены на рис. 3-6. Пунктирными
линиями показаны графики, соответствующие расчету по методу Винера - Хопфа.
Кривые 1 – 3 на рис. 3
получены с помощью решения, описанного выше для ![]() ,
, ![]() . Пунктирная кривая на рис. 3 и 4
соответствует решению методом Винера – Хопфа для бесконечно тонких стенок (
. Пунктирная кривая на рис. 3 и 4
соответствует решению методом Винера – Хопфа для бесконечно тонких стенок (![]() ). Частота
). Частота ![]() равна
60 ГГц. Кривые 1 – 3 на рис. 4 получены для
равна
60 ГГц. Кривые 1 – 3 на рис. 4 получены для ![]() ,
, ![]() . Кривые 1 – 2 на рис. 5 получены с
помощью решения, описанного выше для
. Кривые 1 – 2 на рис. 5 получены с
помощью решения, описанного выше для ![]() ,
, ![]() , а кривые 1 – 2 на рис. 6 получены для
, а кривые 1 – 2 на рис. 6 получены для ![]() ,
, ![]() . Все
размеры приведены в миллиметрах.
. Все
размеры приведены в миллиметрах.
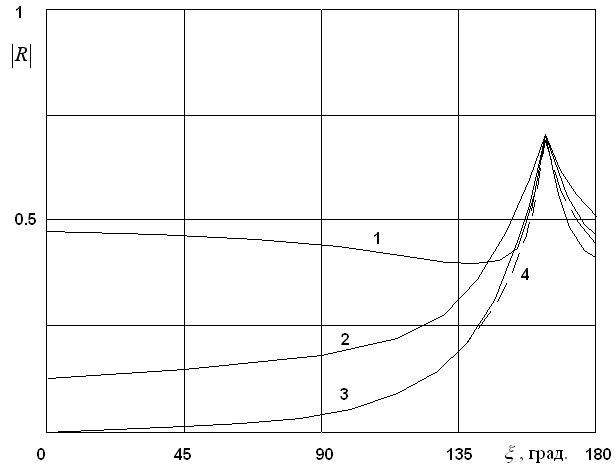
Рис. 3. Зависимость модуля коэффициента отражения от
параметра ![]() при
при ![]()
Геометрические размеры решетки были выбраны так, чтобы при некотором угле сканирования минус первая гармоника Флоке переходила бы в режим распространения. Из рисунка видно, что полученное решение хорошо совпадает с эталонным практически во всем секторе сканирования за исключением небольшого диапазона непосредственно примыкающего к границе сектора сканирования. Очевидно, что достоверность решения повышается с понижением частоты и снижается при ее повышении. В частности оно уже не пригодно для описания переходов через критические условия гармоник Флоке более высоких порядков. В тоже время, наиболее интересная область параметров, соответствующая одно- и двух - модовому режиму решетки описывается вполне удовлетворительно.
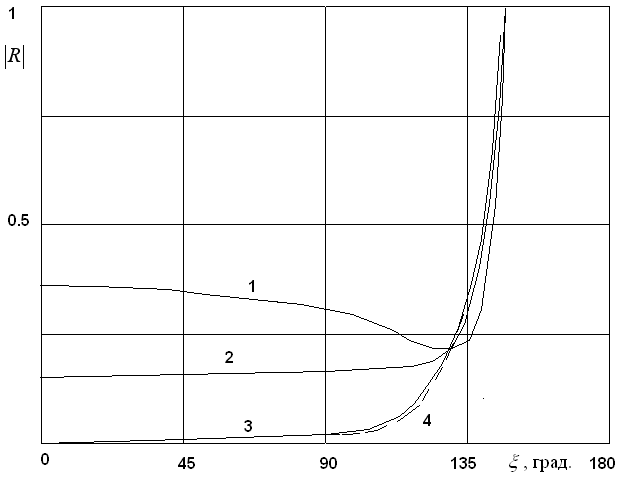
Рис. 4. Зависимость модуля коэффициента отражения от
параметра ![]() при
при ![]()
Численная эффективность предложенного алгоритма весьма высока, поскольку он сводится к решению системы алгебраических уравнений невысокого порядка. Все коэффициенты системы, вычисляются по достаточно простым формулам.
Таким образом, квазистатическое решение электродинамической задачи позволило хорошо описать поведение решетки в наиболее интересной области параметров и создать эффективный численный алгоритм.
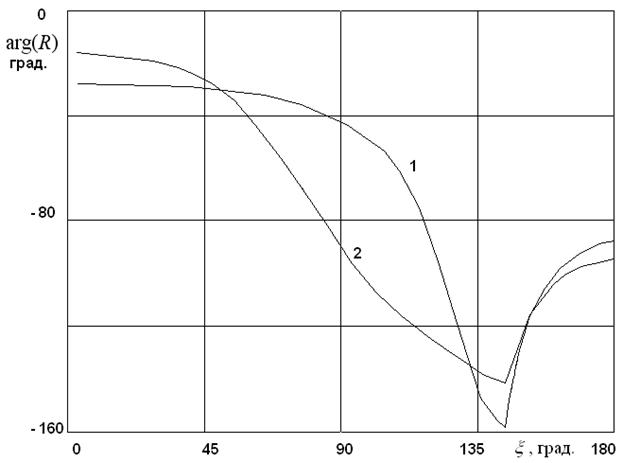
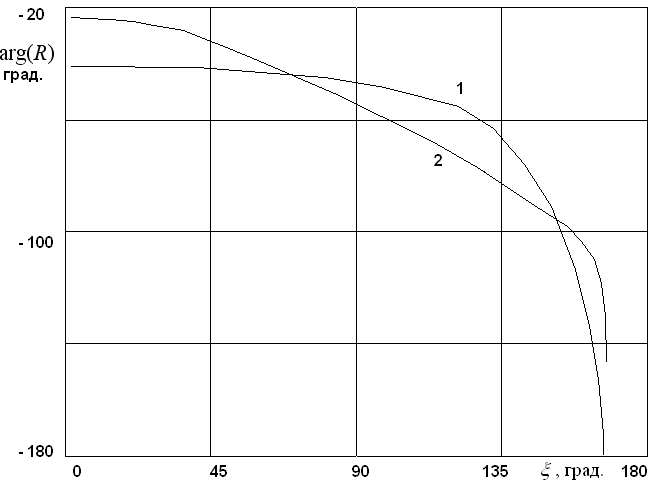
Рис. 5. Зависимость фазы коэффициента отражения от
параметра ![]() при
при ![]()
Рис. 6. Зависимость фазы коэффициента отражения от
параметра ![]() при
при ![]()
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 12-08-12003/12 офи_м).