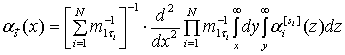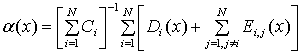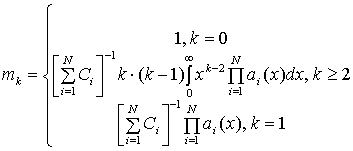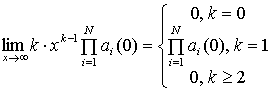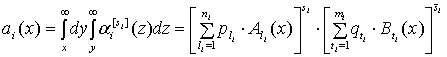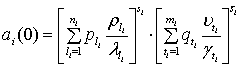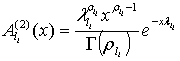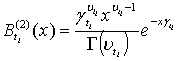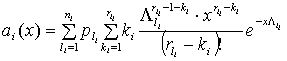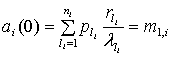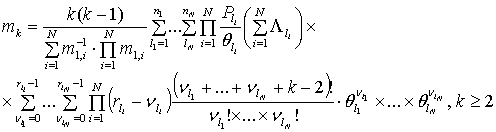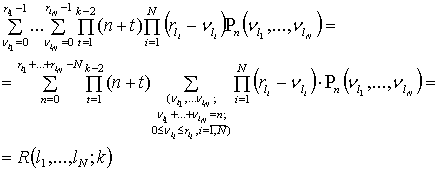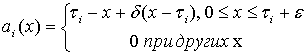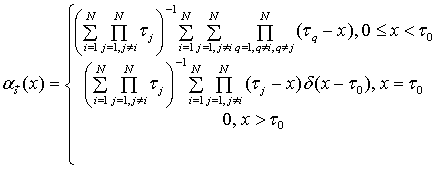УДК 621.391.14:621.396

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И НАЧАЛЬНЫЕ МОМЕНТЫ ДЛИТЕЛЬНОСТИ ИМПУЛЬСОВ ПОТОКА S-СОСТОЯНИЙ

Г. Б. Георгадзе, Ф. В. Голик

Новгородский государственный университет им. Ярослава Мудрого

Статья получена 16 апреля 2014 г.

Аннотация. Предложена методика расчета плотности распределения и начальных моментов времени пребывания суперпозиций потоков прямоугольных импульсов в заданном состоянии. Рассмотрены частные случаи распределения длительностей импульсов и пауз парциальных потоков: смесь гамма-распределений, гиперэрланговское и вырожденное распределения.

Полученные результаты могут использоваться при анализе надежности и эффективности функционирования сложных систем, а так же при оценке параметров асинхронных систем передачи информации.

Ключевые слова. Случайный поток импульсов, суперпозиция потоков, поток совпадений, длительность импульсов, плотность распределения вероятности, начальные моменты.

Abstract. A calculation method of both distribution density and initial moments sojurn time of square wave-form pulses flows superpositions in given state is proposed. Some special cases partial flows of pusses and pauses durations are considered: gamma-distributions superposition, hyper-Erlang distribution and degenerate distribution. These results can be used for analysis of both reliability and effectiveness of complex systems functioning as well for parameters of asynchronous systems of information transmission estimations.

Keywords: stochastic pulses flows, superposition of flows, flow of coincidence, pulses duration, probability density, initial moment.

 

Введение

В [1] доказано, что суперпозиция потоков прямоугольных импульсов при выполнении определенных условий и ограничений адекватно описывается полумарковской моделью. Там же предложена методика расчета одношаговых переходных вероятностей и условных функций распределения длительности пребывания процесса в фиксированном состоянии. Эти характеристики необходимы и достаточны для полного описания суперпозиции случайных потоков прямоугольных импульсов.

На практике встречаются задачи, решение которых может быть получено без подробного исследования процесса суперпозиции. Например, при оценке характеристик асинхронных систем передачи информации бывает достаточно найти вероятностные параметры временного перекрытия информационных пакетов: вероятность совпадения потоков и распределение длительности времени совпадения.

Вопросы совпадения импульсных потоков исследовались в работах В. И. Тихонова, Я. С. Ицхоки, В. А. Дьякова и др. Наиболее полно аспекты теории впервые изложены в монографии Н. М. Седякина [2].

В настоящей работе предложена методика расчета плотности распределения вероятностей и начальных моментов времени пребывания суперпозиции потоков в заданном -состоянии. Результаты базируются на теоретических положениях, полученных Седякиным Н. М., и являются их обобщением применительно к теории многомерных потоков совпадений.

 

2. Условия и ограничения

Будем считать, что парциальные потоки ,  прямоугольных импульсов, образующие суперпозицию , , стационарные и взаимно независимые в совокупности; существуют и заданы плотности распределения вероятностей длительности импульсов  и длительности пауз ; импульсы (паузы), принадлежащие одному и тому же потоку, не перекрываются сами с собой; существуют математические ожидания длительностей импульсов  и пауз .

Процесс  находится в момент  в -состоянии, если , . Во времени эти состояния описываются потоком -состояний

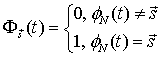
Поток  может быть представлен произведением соответствующих комбинаций парциальных потоков  и их инверсий  [3]:

,

где .

3. Плотность распределения вероятностей времени пребывания процесса 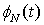 в 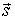-состоянии

Искомая плотность распределения равна плотности распределения длительности импульсов потока  [3]:

                                            (1)

где

,                                                   

,                                                   

, ,

 

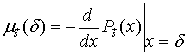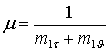
Запишем соотношение (1) в развернутом виде:

,                          (2)

где

                                        (3)

 - плотности распределения длительностей импульсов и пауз потоков ;

.                                            (4)

 

В дальнейшем для сокращения записи, там, где это возможно, будем опускать индекс .

После дифференцирования в (2) получим:

,                  (5)

где

,                                                       

,                                       

,                       

,                                                       

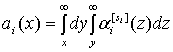.                               (6)

 

Таким образом, вычисление плотности распределения сводится к вычислению функции (6) и ее производных.

4. Начальные моменты времени пребывания процесса 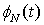 в 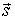-состоянии

Начальный момент порядка  равен

.                                               (7)

 

Подставив (6) в (7), после интегрирования по частям получим

                        (8)

Это выражение справедливо, если выполняются следующие условия:

,                                (9)

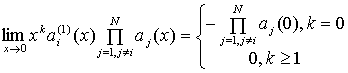                   (10)

                                 (11)

                          (12)

Здесь везде .

Можно показать, что условия (9)...(12) справедливы для плотностей распределения , заданных смесями гамма-распределений, гиперэрланговским и вырожденным распределениями.

Рассмотрим методику вычисления плотностей  и соответствующих им начальных моментов  при конкретных плотностях распределения  компонент парциальных потоков .

5. Смесь гамма-распределений

В этом случае плотности распределения вероятностей длительности импульсов и пауз -го парциального потока равны:

,

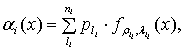
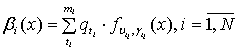где 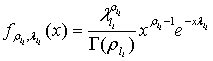 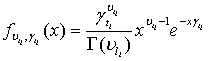- плотности гамма-распределения с параметрами  и  соответственно;

 - весовые коэффициенты, удовлетворяющие условиям:

, .

 

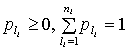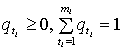Определим плотность распределения , заданную выражением (5), и найдем начальные моменты  в соответствии с формулой (8).
 

5.1. Плотность распределения

Для вычисления  по формуле (5) необходимо определить функции  и их производные :

         (13)

где

,

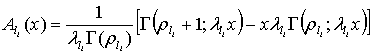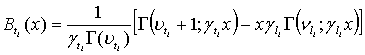                  (14)

 

Здесь  - неполная гамма-функция.

Очевидно

.                                 (15)

 

Дифференцируя , получим:

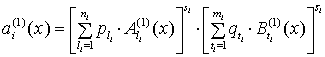,                       (16)

где

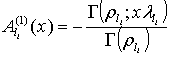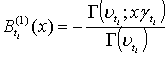; ;                         (17)

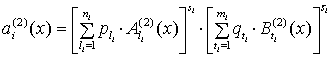,                          (18)

где

, .                   (19)

 

Подставляя в (5) выражения (14)...(19), получим формулу для плотности распределения .

Пример 1. Парциальные потоки, длительности импульсов и пауз которых имеют гамма-распределение с параметрами , , . Тогда

 

 

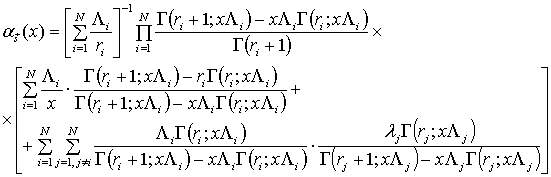
При выводе использовалось соотношение [4;8.356.2]:

.

Пример 2. В условиях примера 1 примем . Тогда используя соотношение [4; 8.352.2]:

получим: . Следовательно, при экспоненциальном распределении длительности импульсов и пауз парциальных потоков, распределение длительности импульсов потока -состояний также экспоненциальное, что совпадает с известным результатом [2].
 

5.2. Начальные моменты

Опуская доказательство выполнения условий (9)...(12) перейдем к вычислению начальных моментов.

Момент первого порядка легко определяется на основании (8) с учетом (15). После несложных преобразований получаем:

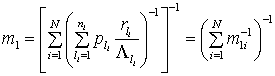                        (20)

где  - начальный момент первого порядка длительности импульсов (пауз) потока; ;

Подставив в (8) при  выражение (13), имеем:

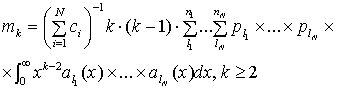                    (21)

Таким образом, вычисление  сводится к определению интеграла от произведения  функций вида

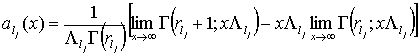,           (22)

 

умноженных на .

Формула для начального момента выражается через  - гипергеометрическую функцию  переменных и достаточно громоздка, поэтому здесь не приводится. Численные значения моментов можно найти по (21).

6. Гиперэрланговское распределение

6.1. Плотность распределения

Определим функцию . Для этого воспользуемся результатами предыдущего параграфа, учитывая, что распределение Эрланга есть частный случай гамма-распределения с параметрами  и , где  - целые положительные числа.

Непосредственно из (13)...(19) получаем:

                              (23)

                                          (24)

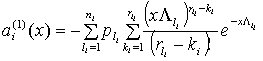                             (25)

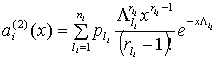                                (27)

Здесь .

Подставив (23)... (27) в (2), получим выражения для плотности распределения длительности импульсов потока - состояния.

Пример 3. Длительности импульсов и пауз парциальных потоков распределены по закону Эрланга: , , ,. Тогда

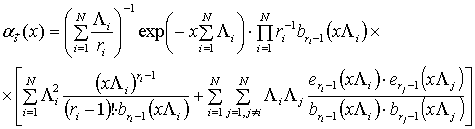
где

,

.

 

При выводе использовалось соотношение с [4; 8.352.2]. Приняв , получим результат примера 2.

Для парциальных потоков  с одинаковыми параметрами распределения длительностей импульсов и пауз и  плотность распределения  равна:

.

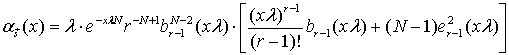При

.
 

6.2. Начальные моменты

Начальные моменты достаточно просто определяются из (8) на основании (23) и (24).

Очевидно, как и раньше

,

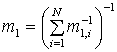где момент  равен (24);

  (28)

где .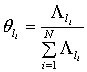

 

Обозначим . Тогда

,

где пустое произведение принято равным 1.

Рассмотрим выражение

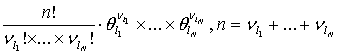.                       (29)

Поскольку , то (29) есть вероятность полиномиального распределения .

Суммы по  можно упорядочить следующим образом:

 

            (30)

где  имеет смысл усредненного с весом  произведения  в области -мерного пространства, заданного системой:
 

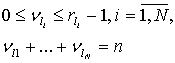
Тогда

.

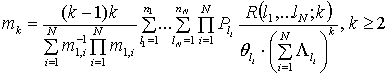Учитывая, что

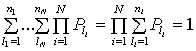
можно рассматривать суммирование по  с весом  как операцию математического ожидания. Следовательно

 

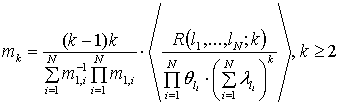                       (31)

Здесь угловые скобки означают усреднение с вероятностями по всем .

Пример 4. Пусть , то есть  - смесь показательных распределений. Тогда из (28) получим

.

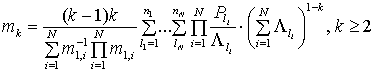Пример 5. Совпадение парциальных потоков с эрланговским распределением длительностей импульсов и пауз. В этом случае , , ,. Тогда из (30) после преобразований получим:

.

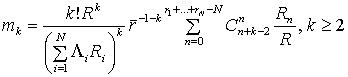Здесь приняты обозначения:

,

.

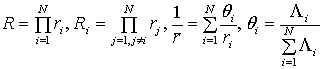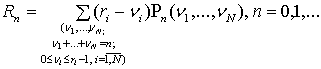7. Вырожденное распределение

7.1. Плотность распределения

Вырожденное распределение можно аппроксимировать распределением Эрланга -го порядка при . Следовательно, результаты для этого случая могут быть получены из предыдущего параграфа путем предельного, перехода в выражениях для  и . Однако непосредственное вычисление по формулам (5) и (8) оказывается более простым.

Пусть плотность распределения  равна:

                                     (32)

где  - дельта-функция, а  - длительность импульса или паузы -го парциального потока.

Тогда

,                         (33)

,                                             (34)

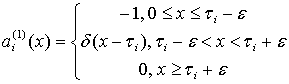,                            (35)

.                                         (36)

Здесь .

Подставляя (33)...(36) в (5) получим

,  (37)

где .

В несколько ином виде выражение для плотности распределения вероятности длительности импульсов потока совпадений получено в [2].
 

7.2. Начальные моменты

Для вычисления начальных моментов представим произведение функций  в (8) в виде суммы:

.

Здесь -  - множество сочетаний  неравных между собой индексов ;

 - произведение  величин , заданных множеством .

Поскольку функции  отличны от 0 на конечных интервалах , то условия (9)...(12) выполняются и формула (8) справедлива. Подставляя (37) в (8) и интегрируя в пределах , получаем:

,

.

 

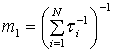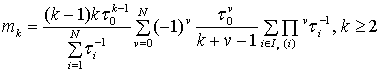Литература

1. Голик Ф. В. Вероятностные характеристики полумарковской модели суперпозиции случайных потоков прямоугольных импулсов. [Электронный ресурс] / «Журнал радиоэлектроники», N 2, 2013, 0.75 п. л. – Режим доступа: http://jre.cplire.ru/jre/feb13/6/text.html, http://jre.cplire.ru/jre/feb13/6/text.pdf

2. Седякин Н.М. Элементы теории случайных импульсных потоков. М.: Сов. радио, -1965.

3. Голик Ф. В. О фундаментальных свойствах многомерных случайных потоков прямоугольных импульсов и сопряженных с ними процессов. /Вестник НовГУ, вып. № 75, т. 1, - 2013.

4. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. – М.: Наука. Гл. ред. физ.-мат. лит., 1971. – 1108 с.

5. Люк Ю. Специальные математические функции и их аппроксимация. – М.: Мир, 1980. – 608 с.