УДК 621.391, 621.317.7
ОЦЕНКА ПОГРЕШНОСТЕЙ ДОПЛЕРОВСКИХ СИСТЕМ
В. Г. Патюков, Е. В. Патюков, Е. Н. Рычков
Институт
инженерной физики и радиоэлектроники Сибирского
Федерального университета
Статья
получена 24 апреля 2014 г.
Аннотация. Рассматриваются вопросы оценок погрешностей в доплеровских измерительных системах. Получены алгоритмы, обеспечивающие существенное уменьшение суммарной погрешности оценки доплеровских частот.
Ключевые слова: плотность распределения случайной частоты, числовые характеристики погрешности дискретизации; оценка погрешности классических устройств; методы снижения суммарной погрешности измерения.
Abstract: Questions of error estimates in dopler measuring systems. Obtained algorithms provide a substantial reduction of the total estimation error dopler frequencies.
Key words: density distribution of the random frequency, the numerical characteristics of sampling error; error estimate classical devices; methods to reduce the total measurement error.
1. Введение
Доплеровские измерительные
системы широко используются при решении различных научно-технических задачах.
Это, в первую очередь, разработка и использование высокоточной радиолокационной
аппаратуры, позволяющей получать оценки скоростей в авиационной и космической
технике, решение вопросов построения различных контрольно-измерительных систем,
отдельных физических, медицинских и других задач. Однако используемые методы
оценки частотно-временных параметров в доплеровских системах не всегда устраивают
разработчиков по вопросам точности и помехоустойчивости. Так, не полно раскрыта
физика процессов при построении высокоточных измерительных систем, уменьшения,
как шумовой составляющей суммарной погрешности, так и погрешности
дискретизации. В данной работе приводятся результаты исследований, обеспечивающие
построение высокоточных доплеровских измерительных систем, позволяющих
уменьшить значения погрешностей практически до потенциально возможных значений,
например, основанных на использовании метода максимума функции правдоподобия [2].
2. Вероятностные характеристики исследуемых сигналов
Одной из моделей сигналов, используемых при анализе помехоустойчивости доплеровских систем, является аддитивная смесь гармонического сигнала и узкополосного случайного процесса, центральная частота энергетического спектра которого в частном, но широко распространенном на практике, случае совпадает с частотой гармонического сигнала [1]:
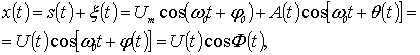
где 
; 
и
- амплитуда, угловая частота и начальная фаза сигнала, а 
и 
- огибающая и фаза случайного процесса
; 
и
- огибающая, случайная фаза и полная фаза аддитивной смеси. Основной
случайной функцией, в доплеровских системах, является мгновенная частота, связанная
с полной фазой аддитивной смеси известным соотношением:
, (1)
где 
и
- производные синфазной и квадратурной составляющих процесса 
; 
- случайная частота, определяемая
через производную фазы аддитивной смеси и характеризующая скорость её изменения.
Как видно из (1), случайный характер изменения мгновенной частоты определяется
характером поведения синфазной 
и квадратурной
составляющих, через которые можно представить
случайный процесс .
Достаточно
полное вероятностное описание характера изменения случайной частоты может быть
получено на основе известной информации о совместной многомерной плотности
распределения огибающей аддитивной смеси, фазы и их производных. В часто
встречающемся случае отсутствия расстройки между частотой сигнала 
и центральной частотой энергетического
спектра квазигармонического дифференцируемого гауссовского шума такая плотность распределения имеет вид [1]:
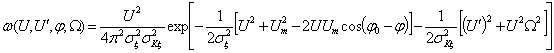, (2)
где 
и
- дисперсии процесса и
его квадратурных составляющих производных.
Выполнив нормировку в (2) относительно дисперсий, получим:
, (3)
где 
; 
;
; 
.
Как следует из (3) случайная частота влияет на характер и общую оценку
совместного распределения амплитуды, фазы и их производных. Для получения совместной плотности
распределения случайной фазы аддитивной смеси и случайной частоты следует выполнить
двойное интегрирование (3) по всем значениям огибающей и её производной:
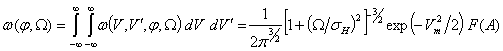, (4)
где 
,
; 
- нормированное среднеквадратическое
значение квадратурных составляющих, 
- функция ошибок [2]. Из (4) видно, что совместное распределение фазы
аддитивной смеси и её производной (случайной частоты) функционально связано
нелинейной зависимостью с нормированными параметрами 
и 
.
Плотность распределения случайной частоты получим из (4) в результате интегрирования
по 
:
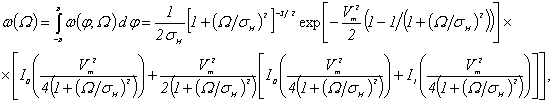(5)
где 
и
– модифицированные функции Бесселя
нулевого и первого порядков от мнимого аргумента. Полученная формула, определяет
вероятностные характеристики случайной частоты аналитически и выражает сложную
функциональную нелинейную связь исследуемого случайного процесса с параметрами и 
.
Результат моделирования (5) представлен графиком на рис. 1.
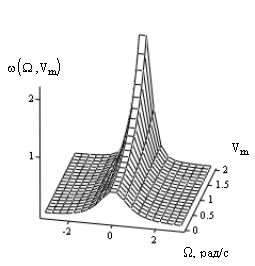
Рис. 1. Плотность распределения случайной частоты.
В соответствии с рис. 1, плотность распределения случайной частоты существенно зависит от сложившегося отношения сигнал/помеха в анализируемой аддитивной смеси. Так, с увеличением нормированной амплитуды сигнала плотность распределения случайной частоты стремится к распределению в виде дельта-функции, подчеркивая тем самым наиболее вероятное значение, равное математическому ожиданию. Интенсивность распределения случайной частоты зависит от исходного значения W и также уменьшается с возрастанием Vm .
Полученные результаты
позволяют характеризовать случайный процесс 
с
различных позиций в зависимости от того, какая информация доступна при
исследованиях в доплеровских системах, определяя тем самым помехоустойчивость
доплеровских измерителей. Кроме того, результаты исследования дают возможность
синтезировать устройства статистической обработки при оценке частотно-временных
параметров сигналов с повышенной точностью и помехоустойчивостью, разрабатывая
устройства, учитывающие вероятностные взаимосвязи.
3. Анализ погрешностей доплеровских измерителей
Одним из основных блоков работы доплеровских измерительных систем является блок статистической обработки, включающий измеритель частоты, обеспечивающий результаты оценки среднего значения мгновенной частоты гармонического сигнала.
Рассмотрим механизм формирования и величину суммарной погрешности в устройствах оценки среднего значения мгновенной частоты с равномерной весовой обработкой (функцией Дирихле), работающих в режиме измерения периода. Точность таких (классических) цифровых устройств оценки среднего значения мгновенной частоты аддитивной смеси гармонических сигналов и узкополосного шума ограничена стабильностью частоты опорного генератора, погрешностью дискретности и погрешностью, обусловленной наличием аддитивных шумов в исследуемом сигнале.
Среднеквадратическое значение суммарной относительной погрешности при оценке среднего из n периодов равно [3]:
где 
- количество усредняемых периодов за
время усреднения (рис. 2); 
- среднеквадратическое значение
погрешности дискретизации при оценке значения одного периода сигнала, а 
- период следования счётных импульсов; 
- составляющая суммарной погрешности, обусловленная нестабильностью
частоты генератора образцовых импульсов. Стабильность современных генераторов
можно получить достаточно высокую, поэтому при больших отношениях сигнал/шум
основную долю суммарной погрешности будет составлять погрешность дискретизации,
которая при высоких требованиях к точности оценки среднего значения мгновенной
частоты, например, стабильного гармонического сигнала, имеет существенное
значение.
4. Разработка оптимизированного алгоритма
На рис. 2, приведена
временная диаграмма работы классического цифрового устройства оценки среднего значения мгновенной частоты (начало измерения
перенесено в центр графика), работающего в режиме измерения периода, значение
оценки которого равно: 
,
где 
и 
- моменты времени, соответствующие началу и концу суммарного
времени измерения периодов исследуемого сигнала, следующих через 
. Погрешности дискретизации состоят из погрешностей
- “начала” и погрешностей “конца” - 
,
начала и конца измерения i-го
периода (рис. 2) и распределены равновероятно в интервале 
с плотностью распределения 
, поэтому дисперсии 
и 
будут
равны:
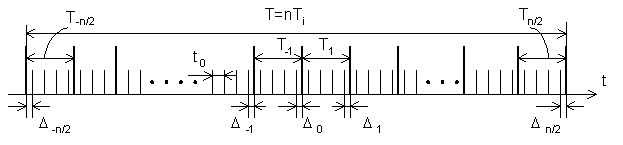
Рис. 2. Формирование погрешности дискретизации.
Определим дисперсию погрешности дискретизации по общим правилам при усреднении n периодов сигнала:
, (6)
где R - коэффициент корреляции погрешностей начала и конца
суммарного времени измерения – 
и 
. К – количество усреднений.
Из (6), при R = 0, получим дисперсию оценки
частотно-временного параметра при независимых значениях погрешностей равную: 
Следовательно, дисперсию погрешности
дискретизации классического устройства оценки частотно-временного параметра
можно снизить, если уменьшить период следования импульсов опорного генератора 
, но это ограничено быстродействием
используемой элементной базы. Можно увеличить n, то есть время усреднения, однако это не всегда
представляется возможным.
По этой причине при построении цифровых устройств оценки среднего значения мгновенной частоты, актуальной является задача поиска алгоритмов, обеспечивающих уменьшение дисперсии оценки без увеличения времени усреднения.
Суммарная
погрешность дискретизации результата усреднения в соответствии с рис. 2 будет
равна: 
где 
- весовые коэффициенты i-го результата усреднения (при
дополнительном условии, исключающем смещение оценки –
). Если использовать дискретный вариант
«треугольной» весовой функции (функции Бартлетта) при обработке результатов
оценки 
, то суммарная погрешность будет
равна [3]:
.
Преобразуя полученное
выражение и учитывая, что погрешность измерения «начала» измерительного
интервала одновременно является погрешностью
«конца» интервала 
с отрицательным
знаком, в результате, при независимых погрешностях 
и
в i -м интервале, получим:
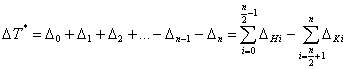. (7)
Из (7) следует, что при весовой обработке наблюдается автоматическая компенсация погрешностей, а дисперсия оценки, найденная по общим правилам, будет равна:
. (8)
Таким образом, по сравнению
с (6) рассматриваемая весовая обработка приводит к существенному снижению
погрешности дискретизации [3]. Однако, при использовании весовой обработки,
необходимо решить задачу поиска оптимизированного алгоритма, обеспечивающего
получение предельного значения дисперсии оценки частотно-временных параметров в
доплеровских системах. Для определения такого алгоритма будем исходить из того,
что имеется информация о результатах измерения всех усредняемых периодах 
(рис. 2). В этом случае оценка будет равна:
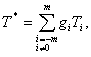(9)
где m=n/2.
При такой обработке задача уменьшения погрешности сводится к
оптимизации весовых коэффициентов 
,
обеспечивающих минимальную дисперсию оценки 
при
постоянном времени усреднения. При оценке периода сигнала по формуле (9)
погрешность отсчёта начала i-го
периода связана жесткой функциональной зависимостью с погрешностью отсчёта
конца (i-1)-го периода (рис. 2). Учитывая эту связь, выражение для
суммарной погрешности оценки среднего значения периода можно представить в
виде:
.
Найдём
дисперсию суммарной погрешности 
по общим
правилам:
,
где 
.
Значения весовых коэффициентов, обеспечивающих минимумы полученного выражения, найдем методом неопределённых множителей, определяя экстремум функции [2]:
.
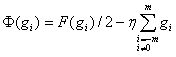(10)
Дифференцируя (10) по и приравнивая производные нулю, получим систему
алгебраических уравнений вида:
и
или
,
при i =2, 3, 4…m;
, при i =-2, -3, -4…-m.
Выразив через 
и
в результате получим:
, при i>0;
, при i<0. (11)
Для 
и 
из
(11) получим систему уравнений:
решение которых относительно 
, даёт:
.
Отсюда следует, что 
и, следовательно, весовая функция должна
быть симметричной относительно середины времени усреднения. Из условия
несмещённости оценки 
определим и получим общее выражение для весовых
коэффициентов, минимизирующих дисперсию оценки частотно-временных параметров:
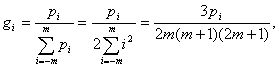(12)
где 
а знаменатель преобразован с учётом соотношений
и 
.
Используя (12), получим аналитическое выражение (9), характеризующее работу доплеровского измерителя, обеспечивающего практически предельную точность оценки периода исследуемого сигнала:
. (13)
дисперсию оценки (13) в результате получим:
,
которая при m>>1, пренебрегая относительно малыми величинами в знаменателе и, переходя к n , принимает окончательный вид:
. (14)
5. Выводы
Сравнение дисперсии (14),
оптимизированного алгоритма обработки и классического метода нахождения оценки
частотно-временных параметров сигналов (6) при R = 0, в доплеровских измерителях показывает, что, при
одном и том же времени усреднения, весовая обработка Тi позволяет снизить погрешность
квантования по уровню в n/6
раз. Так, например, при Т = 1 с, 
и
периоде сигнала 
с, относительное
среднеквадратическое значение погрешности дискретизации классического
устройства равно 
, а устройства,
реализованного в соответствии с выражением (13) – 
.
Следовательно эффективность использования алгоритма (13) более чем на два
порядка выше классического метода при том же времени усреднения.
Оптимизированный алгоритм, использующий изменения весовых коэффициентов по формуле (13), позволяет существенно уменьшить погрешность дискретизации и тем самым повысить точность оценки частотно-временных параметров доплеровских систем. При этом одновременно снижается и шумовая составляющая суммарной погрешности измерения в зависимости от корреляционных особенностей исследуемых сигналов.
1. Тихонов, В.И. Нелинейные преобразования случайных процессов / В. И. Тихонов. - М.: Радио и связь, 1986. - 259 с.
2. Корн, Г. Справочник по математике для научных работников и инженеров / Г. Корн, Т. Корн. - М.: Наука, 1978. - 831 с.
3. Патюков В. Г. Фильтрация сигналов при оценке частотно-временных параметров. Журнал радиоэлектроники: электронный журнал. 2003. №5. URL: http://ire.cplire.ru/win/may03/2/text.html