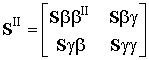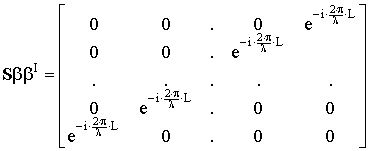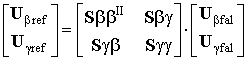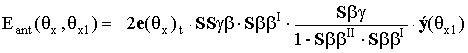"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2014

оглавление

УДК 621.396.677

ХАРАКТЕРИСТИКИ РАССЕЯНИЯ ЛИНЕЙНЫХ ВИБРАТОРНЫХ РЕШЕТОК ВАН-АТТА

 

А. А. Кузнецов

Институт сервиса и туризма Донского государственного технического университета

 

Статья получена 23 марта 2014 г., после доработки – 5 мая 2014 г.

Аннотация. С использованием аппарата матриц рассеяния получены выражения для структурной и антенной составляющих поля рассеяния линейной вибраторной решетки Ван-Атта. Матрица рассеяния входов вибраторов найдена через их матрицу сопротивлений, для определения которой применён метод наведённых ЭДС. Определено влияние длины соединительных фидеров на уровень структурной и антенной составляющих поля рассеяния решётки Ван-Атта при различной ориентации вибраторов, а также оценено влияние на него взаимной связи между вибраторами.

Ключевые слова: антенная решетка Ван-Атта, диаграмма направленности рассеянного поля.

Abstract: The expressions for structural and antenna components of scattering field of linear vibrating array of Van-Atta are obtained on the base of scattering matrix technique. The matrix of dispersion of entrances of vibrators is found through their matrix of resistance which is determined by a method of induced EDS. Determined the influence of the length of connection feeders to the level of structural and antenna components of scattering field of linear vibrating array of Van-Atta at various orientation vibrators, also evaluated the influence of the mutual ties between vibrators.

Key words: antenna array of Van-Atta, directional patterns of a scattered field.

 

Введение

Характеристики рассеяния антенных решёток различных типов исследовались во многих работах, в том числе в [1] – [6]. Актуальность этих исследований обусловлена необходимостью снижения радиолокационной заметности объектов, имеющих в своем составе антенные решетки, а также необходимостью обеспечения электромагнитной совместимости систем, антенны которых расположены в непосредственной близости друг от друга. Среди антенных решёток (АР) особое место занимают решетки Ван-Атта, основное предназначение которых – ретрансляция падающей волны в обратном направлении. Характеристики рассеяния решёток Ван-Атта исследовались в работах [2], [4].

В работе [2] рассмотрен случай падения плоской волны на эквидистантную линейную АР из 8 полуволновых вибраторов в свободном пространстве. Вибраторы, расположенные симметрично относительно центра АР, соединены попарно фидерами одинаковой длины, образуя решетку Ван-Атта. С использованием аппарата матриц рассеяния проведено математическое моделирование поля рассеяния с учетом изменяемого параметра – длины соединительного фидера между излучателями. К сожалению, в работе [2] рассмотрена не реальная решётка Ван-Атта, поскольку реальная вибраторная решётка функционирует не в свободном пространстве, а при наличии корпуса с элементами системы, обслуживаемой решёткой. Кроме того, в работе [2] рассмотрены только частные случаи прихода падающей волны: по нормали и вдоль оси.

В [4] рассмотрен случай рассеяния плоской электромагнитной волны на решетке Ван-Атта с излучателями в виде плоскопараллельных волноводов в бесконечном плоском экране. Для двумерной задачи рассеяния на решетке Ван-Атта получено приближенное решение без учета взаимного влияния излучателей через верхнее полупространство и с учетом взаимодействия между элементами через линии передачи с основным типом волны.

В известной литературе не рассмотрены характеристики рассеяния вибраторных решёток Ван-Атта при наличии объектов, на которых размещены вибраторы при различных направлениях падающей волны.

Целью работы является определение влияния длины соединительных фидеров на уровень поля рассеяния решётки Ван-Атта при наличии корпуса объекта и различных ориентациях вибраторов, а также оценка влияния на него взаимной связи между вибраторами.

Для достижения указанной цели в работе решается следующие задачи:

- построение математической модели Е- и Н-плоскостных[1] вибраторных решеток Ван-Атта при наличии бесконечного идеально проводящего экрана;

- проведение на основе разработанной математической модели численных экспериментов по определению зависимости уровня рассеянного поля от длины соединительных фидеров;

- проведение на основе разработанной математической модели численных экспериментов по анализу влияния взаимной связи между вибраторами на уровень поля, рассеянного решеткой Ван-Атта.

Постановка задачи.

Положим, что Е- или Н-плоскостная линейная решётка вибраторов расположена в плоскости X0Y над бесконечным идеально проводящим экраном на высоте h (рис. 1). Длина вибраторов 2l. Шаг вибраторов d. Количество вибраторов N. Пары вибраторов, расположенных симметрично относительно центра решетки, соединены фидерами одинаковой длины L с волновым сопротивлением W. На решетку падает волна, поляризованная параллельно или перпендикулярно, с направления, определяемого углом . Требуется построить математическую модель описанной электродинамической системы и на ее основе исследовать влияние на поле рассеяния АР длины соединительных фидеров и взаимной связи между излучателями при различных направлениях падения волны.

 

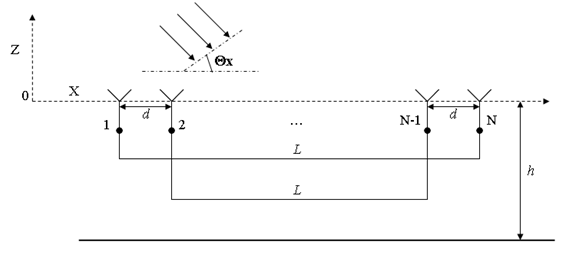
Рис. 1. Схема решетки Ван-Атта

Математическая модель.

Блочная структура системы представлена на рис. 2. Цифрами I и II обозначены соответственно нагрузочный многополюсник (фидеры, соединяющие излучатели, расположенные симметрично относительно центра АР) и антенное полотно. Греческими буквами обозначены соответствующие сечения входов блоков системы, причём входы  соответствуют дальней зоне АР. На входах блоков системы обозначены также нормированные напряжения падающих и отражённых волн.

 

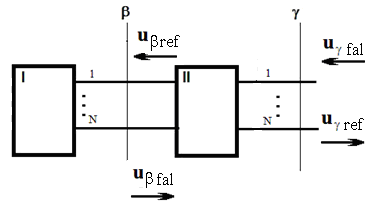
Рис. 2.  К построению матрицы рассеяния АР Ван-Атта

Будем искать выражение для поля рассеяния. Как и в [2], для построения матрицы рассеяния  антенной системы используем матрицы рассеяния нагрузочного 2N-полюсника  и антенного полотна в виде 4N-полюсника :

  и  .                                  (1)

 

Индексами  обозначены N входов нагрузочного многополюсника, соединяющих его со входами вибраторов,  -  выходов антенного полотна. Под выходами последнего будем понимать  ортогональных парциальных характеристик направленности [2].

Перейдём к конкретизации элементов матриц рассеяния , . Матрица  связывает векторы нормированных напряжений падающих и отражённых волн на входах фидеров ():

,                                                       (2)

где:

,                       (3)

где  - длина соединительного фидера в длинах волн ;

 - коэффициент длины фидера в длинах волн.

Матрица  связывает векторы нормированных напряжений падающих и отражённых волн, как на входах вибраторов (), так и в пространстве ():

.                                    (4)

Используя результаты работы [2], запишем выражения для блоков матрицы :

;                                               (5)

;                                                     (6)

;                                                     (7)

.                                   (8)

 

В выражении (8) - эрмитово сопряжение матрицы,  - единичная матрица,  означает матрицу нормированных сопротивлений входов вибраторов. Матрица сопротивлений вибраторной АР над бесконечным проводящим экраном в данной работе найдена методом наведённых ЭДС [7] с использованием функции Грина полупространства. Через  обозначена так называемая ортогонализующая матрица токов [2]:

,                                                (9)

каждому столбцу которой соответствует одна из  ортонормированных характеристик направленности линейки вибраторов :

,   или    .             (10)

Через  обозначена ДН изолированного элемента;  - вектор-столбец ДН элементов АР,  - вектор-столбец ортонормированных характеристик направленности АР. Угол  отсчитываются от положительного направления оси 0x. Как показано в [2], вид ортогонализующей матрицы токов не принципиален, так как она в конечных выражениях отсутствует.

Определив блоки матриц , , перейдём к построению математической модели данной антенной системы, конкретизируя вид матрицы рассеяния всей системы как 2N-полюсника.

Представим выражение (4) в линейном виде:

,                                 (11)

.                                      (12)

Далее подставим выражение (2) в (11) и (12) поочередно:

,                       (13)

,                          (14)

Подставим (13) в (14):

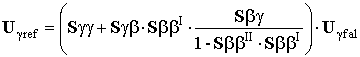          (15)

Первое слагаемое в (15) определяет структурную (неуправляемую) составляющую поля рассеяния (res), а второе – антенную составляющую (ant) [6].

Для диаграмм направленности структурной и антенной составляющих рассеянного поля получены следующие представления:

,             (16)

.            (17)

Через  обозначен вектор-столбец из ЭДС холостого хода на входах вибраторов при падении на решётку плоской волны с направления  [2].

Заметим, что здесь рассмотрение ограничено так называемой «параллельной», то есть взаимодействующей с вибраторами составляющей падающего поля, зависящей от расположения излучателей решетки Ван-Атта.

Численные результаты

Математическое моделирование проведено на решетке Ван-Атта, состоящей из восьми симметричных вибраторов, расположенных в одной плоскости, длина каждого из которых 2l=. Вибраторы расположены над бесконечным идеально проводящим экраном на расстоянии h=. Рассмотрены Е- и Н-плоскостные линейки вибраторов. Предполагается, что на АР падает электромагнитная волна с направлений . Рассмотрены случаи параллельной и перпендикулярной поляризации падающей волны для Е- и Н-плоскостных решеток Ван-Атта соответственно. Изменению подлежала длина соединительного фидера между излучателями L (от  до  с шагом ) при условии наличия взаимной связи между излучателями и без нее.

На рис. 3 - 11 приведены результаты математического моделирования.

На рис. 3 - 5 приведены зависимости уровней антенной составляющей поля рассеяния решетки Ван-Атта от длины фидера между излучателями при различных направлениях падения волны (900, 600, 450), а также при учете взаимной связи между излучателями либо при её игнорировании.

Рис. 3. Зависимость уровня антенной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления

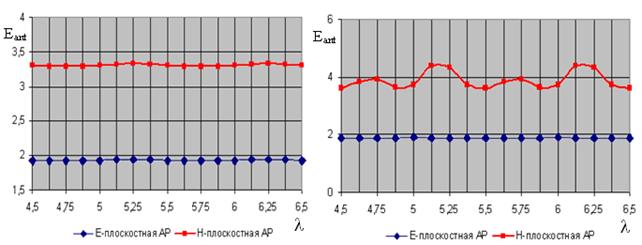
Рис. 4. Зависимость уровня антенной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления


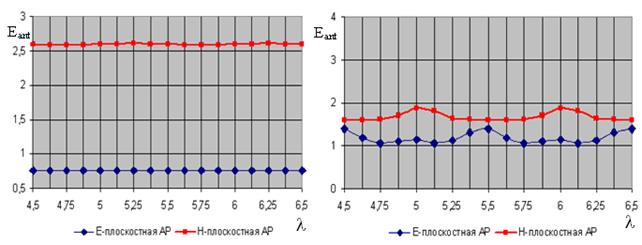
Рис. 5. Зависимость уровня антенной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления

Из рис. 3 – 5 следует, что зависимость уровня антенной составляющей поля рассеяния от длины фидера L носит периодический характер с периодом . Наиболее четко выражены точки экстремума при нормальном падении волны на решетку, это характерно как в случае учета взаимной связи между излучателями, так и при её игнорировании (рис. 3). Проведенные расчеты показали, что антенные составляющие поля рассеяния Н- и Е-плоскостных линеек вибраторов, имеют точно такие же формы, как соответствующие ДН на передачу Н- и Е-плоскостных линеек вибраторов.

Для Н-плоскостных линеек вибраторов характерны более высокие значения уровней антенных составляющих поля рассеяния, чем для Е-плоскостных. Это объясняется более сильной взаимной связью между излучателями, когда они расположены параллельно, а не коллинеарно.

Отсутствие связи между излучателями позволяет идеально согласовать вибраторы с фидерами. При учете взаимной связи между излучателями, происходит рассогласование входов вибраторов с фидерами, что приводит к изменению диаграммы направленности антенной составляющей поля рассеяния (уровни повышаются).

На рис. 6 приведена зависимость уровня антенной составляющей поля рассеяния от направления падения волны. При изменении направления падения волны  от 50 до 900, уровни диаграммы направленности антенной составляющей поля рассеяния увеличиваются.



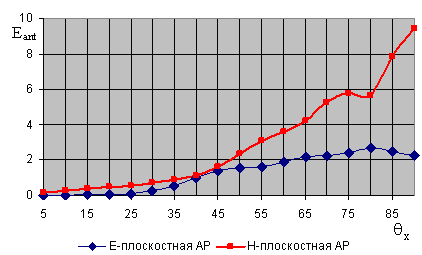
Рис. 6. Зависимость уровня антенной составляющей поля рассеяния

 решетки Ван-Атта от направления падения волны.

 

На рис. 7 - 9 приведены зависимости уровней структурной составляющей поля рассеяния решетки Ван-Атта от длины фидера между излучателями при различных направлениях падения волны (900, 600, 450), а также при учете взаимной связи между излучателями либо при её игнорировании.



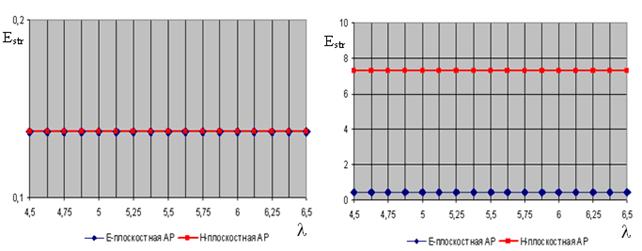
Рис. 7. Зависимость уровня структурной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления

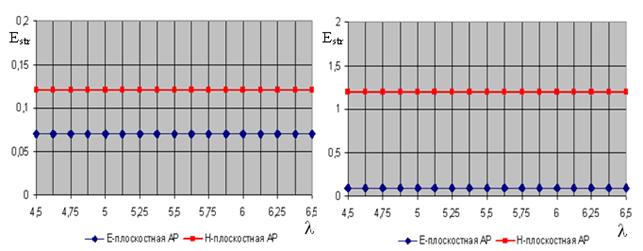
Рис. 8. Зависимость уровня  структурной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления

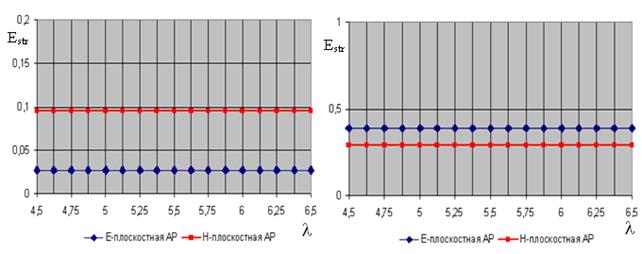
Рис. 9. Зависимость уровня структурной составляющей поля рассеяния от длины фидера при игнорировании (слева) и при учете (справа) взаимной связи между излучателями и падении волны с направления

 

Известно ([5] - [6]), что форма структурной составляющей поля рассеяния не зависит от нагрузки, в данном случае от длины соединительных фидеров. Также известно, и это подтверждается проведенными исследованиями, что максимум диаграммы направленности структурной составляющей поля рассеяния решетки Ван-Атта ориентирован в направлении, зеркальном относительно направления падающей волны. Анализ рис. 7 – 9 свидетельствует, что уровень структурной составляющей зависит от направления падения волны: он максимален при нормальном падении волны на решетку и уменьшается в случае приближения направления падающей волны к горизонту. Из представленных рисунков видно, что при учете взаимной связи между излучателями, которая приводит к рассогласованию предварительно согласованных входов вибраторов, уровень структурной составляющей поля рассеяния выше, чем при ее игнорировании. На структурную составляющую поля рассеяния также влияет взаимное расположение излучателей в решетке: для Н-плоскостных линеек вибраторов характерен более высокий уровень структурной составляющей поля рассеяния, чем для Е-плоскостных линеек, что объясняется более сильной взаимной связью между излучателями в Н-плоскостной линейке.

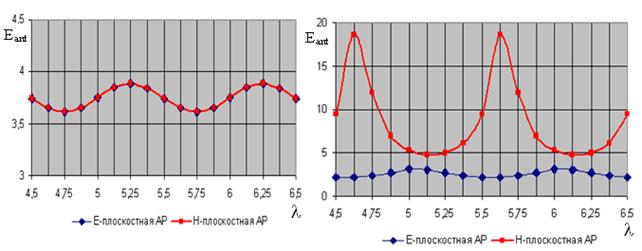
На рис. 10, 11 приведены суммарные диаграммы рассеяния решетки Ван-Атта при игнорировании и при учете взаимной связи между излучателями. Направление падения волны 450, длина соединительных линий L=. Для Е-плоскостной линейки вибраторов при игнорировании взаимной связи между излучателями характерен меньший уровень диаграммы направленности поля рассеяния, чем при учете взаимной связи. Для Н-плоскостной линейки вибраторов влияние взаимной связи между излучателями при заданных исходных данных приводит к увеличению уровня боковых лепестков, в результате чего происходит перераспределение энергии, и уровень главного лепестка понижается (рис. 9, 10, 11).

Из рис. 3 – 8 видно, что структурные составляющие поля рассеяния решётки Ван-Атта имеют более низкий уровень, чем антенные составляющие. Таким образом, суммарные диаграммы направленности поля рассеяния определяются антенными составляющими поля рассеяния, а максимумы структурных составляющих, ориентированные зеркально по отношению к направлению падающего поля, на этом фоне не всегда заметны (рис. 10, 11).

Рис. 10. Суммарные диаграммы рассеяния для Е-(слева) и Н-(справа) плоскостных решеток Ван-Атта, при учете взаимной связи между излучателями

 

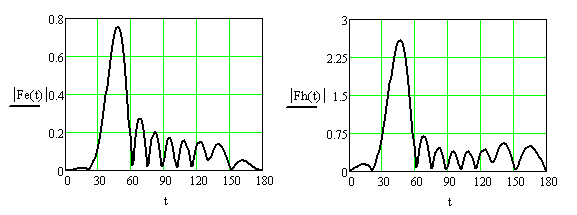
Рис. 11. Суммарные диаграммы рассеяния для Е-(слева) и Н-(справа) плоскостных решеток Ван-Атта, при игнорировании взаимной связи между излучателями

 

Выводы

1. Построенная с использованием аппарата матриц рассеяния модель линейной решетки Ван-Атта, вибраторы в которой расположены над идеально проводящим экраном, позволяет рассчитывать диаграммы направленности структурной и антенной составляющих поля рассеяния.

2. Антенная составляющая поля рассеяния, имеет точно такую же форму, как соответствующая ДН на передачу. Её уровень зависит от расположения вибраторов в решетке, от направления падения волны и от длины соединительных фидеров.

Зависимость уровней антенной составляющей поля рассеяния решётки Ван-Атта от длины фидера между излучателями носит периодический характер с периодом .

Отсутствие связи между излучателями позволяет идеально согласовать вибраторы с фидерами. При этом учёт взаимной связи между излучателями, приводит к рассогласованию входов вибраторов с фидерами, что вызывает повышение уровня антенной составляющей поля рассеяния.

3. Уровень структурной составляющей поля рассеяния не зависит от длины соединительных фидеров, но зависит от направления падения волны. На уровень диаграммы направленности структурной составляющей поля рассеяния, максимум которой ориентирован зеркально по отношению к направлению падающего поля, также влияет взаимное расположение излучателей в решетке: для Н-плоскостных линеек вибраторов характерен более высокий уровень структурной составляющей поля рассеяния, чем для Е-плоскостных линеек.

 

Литература

         1. Бененсон Л.С., Фельд Я.Н. Рассеяние электромагнитных волн антеннами (обзор)// Радиотехника и электроника, 1988, т. 33, №2, с. 225 – 245.

         2. Сазонов Д.М. Основы матричной теории антенных решёток // Сборник научно-методических статей по прикладной электродинамике. – М.: Высшая школа, 1983, с. 111-162.

         3. Пономарёв Л.И., Попов В.В. Рассеивающие свойства антенн и фазированных антенных решёток: Монография. _ М.: Изд-во РУДН, 2003. – 144 с.

         4. Привалова Т.Ю., Синявский Г.П., Юханов Ю.В. Анализ характеристик рассеяния двумерной решетки Ван-Атта// Электромагнитные волны и электронные системы, 2007 г., №5.

         5. Мануилов Б.Д., Кузнецов А.А. Характеристики рассеяния плоских вибраторных решёток при формировании «многолучевых» диаграмм направленности // Антенны, 2012, №1, с. 34 – 42.

         6. Мануилов Б.Д., Кузнецов А.А. Характеристики рассеяния плоской вибраторной решётки фазовой моноимпульсной системы // Электронный журнал «Журнал радиоэлектроники», №2, 2013.

7. Айзенберг Г.З., Белоусов С.П., Журбенко Э.М. и др. Коротковолновые антенны / Под ред. Г.З. Айзенберга. – М.: Радио и связь, 1985. – 536 с. 


[1] В Е-плоскостной решетке оси вибраторов совпадают с осью решетки. В Н-плоскостной решетке оси вибраторов перпендикулярны оси решетки.