|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2006 |
|
СТРУКТУРНЫЙ АНАЛИЗ НА ОСНОВЕ МОДЕЛИ САМООРГАНИЗАЦИИ БИОСТРУКТУР
Красноярский государственный технический университет
Получена 25 ноября 2006 г.
Для биоструктур как для открытых систем характерна универсальная особенность – возможность самоорганизации. Наиболее физически адекватной моделью динамических структур является их описание как системы связанных нелинейных осцилляторов.
Для обнаружения и обработки информации необходимо знание существенных признаков и адекватное описание процессов и явлений, а известно, что целое обладает иными свойствами, нежели его части.
Созданную в 70-х годах И. Р. Пригожиным теорию самоорганизации в определенном смысле уместно назвать теорией структурообразования. Как неравновесная термодинамика она является фундаментальной теорией анализа систем, элементы которых при конденсации вступают во взаимодействие и объединяются связями в структуры. Универсальность теории заключается в её применимости для анализа микро- и макроструктур в косвенных и живых системах.
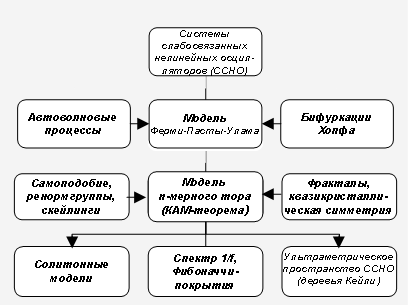
Свойства структур могут быть изучены методами динамики, а некоторые свойства динамических систем можно определить структурными методами. Согласно основным положениям теории самоорганизации структурно-устойчивой является конденсированная диссипативная система – открытая система с внутренним трением, где под внутренним трением понимается переход свободной энергии в энергию связей системы. В работе рассматривается концептуальная система динамического анализа самоорганизующихся процессов и систем, связывающая такие модели и понятия, как автоволновые модели, модель "кубической решетки" Ферми-Пасты-Улама (модель "возврата" ФПУ), теорему Колмогорова–Арнольда–Мозера (КАМ–теорему), модель n-мерного тора, фрактальность с квазикристаллической симметрией природных процессов и систем, их пространственно-временную симметрию и характерные спектры типа 1/f [1].
Общим для открытых систем, обладающих хаотическим поведением, является иерархия цикличностей в их эволюции в виде системы слабосвязанных нелинейных осцилляторов (ССНО), формирующих структуры, связи между которыми можно представить моделью "возврата" ФПУ. Решение проблемы ФПУ было получено в начале 60-х годов М. Крускалом и Н. Забуским, доказавшим, что система Ферми-Пасты-Улама представляет собой разностный аналог уравнения Кортевега-де Вриза (КДВ), и что равнораcпределению энергии препятствует солитон (термин, предложенный H. Забуским), переносящий энергию из одной группы мод в другую. За счет нелинейных связей моды перестают быть независимыми и, энергия медленно (по сравнению с их периодами) переходит в более низкочастотные моды. Бесконечномерный континуум возмущений системы переходит в набор автомодельных (самоподобных) состояний, мод определяющих порядок системы. В открытых нелинейных системах возникает упорядоченность или самоорганизация.
Рис. 1. Система динамического анализа самоорганизующихся процессов и систем
Хаотическое поведение в области сепаратрис – свойство нелинейных осцилляторов. За счет бифуркаций в ССНО происходит переход к хаосу и возможно развитие фрактальных структур. Хаос обретает тонкую структуру масштабно-инвариантного самоподобного множества фракталов или странного аттрактора. Процессы и системы с самоподобной фрактальной структурой целесообразно исследовать с позиций ренормгруппового анализа [2]. Фрактальное множество может быть представлено иерархическим деревом Кейли [3].
Впервые решение вопроса о вечной устойчивости системы было дано теорией Колмогорова–Арнольда–Мозера. КАМ-теорема объясняет механизмы и условия формирования фрактальных структур на основе n-мерного тора. Если отношение частот равно рациональному числу, возникает резонанс, если иррациональному числу – траектория никогда не замкнется. Наилучшим в этом смысле будет иррациональное отношение частот мод,
– так называемое "золотое сечение", генерирующее ряд Фибоначчи. Ряд Фибоначчи является фундаментальным масштабным законом самоподобия (скейлингом) в природе.
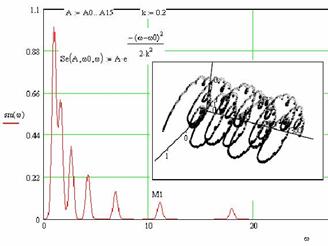
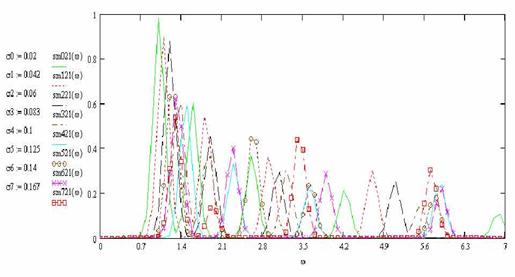
Определим модель ССНО как траекторию и спектр осцилляторов, отношения частот, амплитуд и фаз которых соответствуют ряду Фибоначчи. На рис. 1 приведен расчет такой модели, то есть:
, (1)
где
- начальная функция без возмущений, i=
.
Для модели ССНО с самоорганизацией:
(2)
– функции, в которых амплитуда, фаза и частота изменяются по отношению к начальной функции в иррациональном соотношении "золотого сечения".
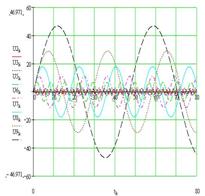
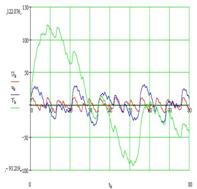
Суммирование осцилляторов показывает формирование одиночных волн (солитонов), которые переносят энергию колебаний в низкочастотный спектр (рис. 2, а,б,в), как это было показано М. Крускалом и Н. Забуским. Формирование спектральной характеристики вида 1/f происходит за счет перераспределения энергии в спектре связанных осцилляторов в сторону низкочастотных мод по мере увеличения количества осцилляторов.
а
б
в
Рис. 2. Формирование солитонов (б) в системе связанных осцилляторов (а) и перераспределение энергии в сторону НЧ-мод в спектре ССНО (в)
Для статистической модели шума 1/f представим параметры его мод нормально распределенными, т. е.
и
, где
и
– случайные возмущения амплитуд и частот спектральных составляющих, распределенных по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением
и
(рис. 3).
а
k=0.05
k=0.15
k=0.5
k=0.75
б
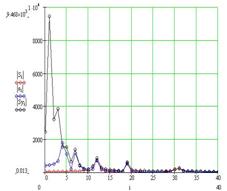
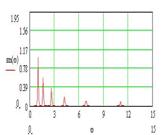
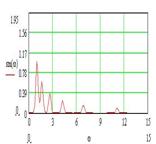
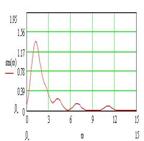
Рис. 3. Спектр ССНО (а) и механизм формирования спектральной характеристики вида 1/f (б), в зависимости от коэффициента связи k
Спектр такой системы будет:
(3)
Здесь:
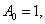
i = 1,…, n;
;
.
Здесь также видно формирование спектральной характеристики вида 1/f за счет перераспределения энергии в спектре связанных осцилляторов в сторону низкочастотных мод в зависимости от коэффициента связи k.
При критических значениях энергии возмущения
происходит разрушение тора и перестройка ССНО в мультифрактальную структуру (рис. 4).
Рис. 4. Формирование спектральной характеристики вида 1/f из-за наличия инфрачастот (а) и разрушение тора при критических значениях
для ССНО
Cинергетический подход к анализу явлений в биоструктурах, где критерием нормы является структурная устойчивость на всех уровнях иерархии биосистем, позволяет перейти от их феноменологического описания к физико-математическим моделям.
Человеческий организм правомерно представить как открытую диссипативную систему с внутренним трением, а гомеостаз как систему слабосвязанных нелинейных эндогенных осцилляторов (ССНО), взаимодействующих с экзогенными циклами окружающей среды. Многоуровневая иерархическая регуляторная система с циклами разной периодичности эволюционно согласована с экзогенными факторами и обеспечивает равновесие организма с экосферой в рамках естественных циклов.
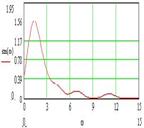
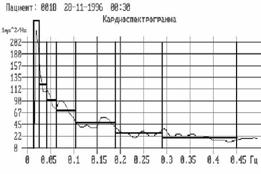
При диагностике функционального состояния важно определить критерии нормы и патологии работы и адаптивные возможности гомеостаза по кардиоритму (КР). Нелинейную динамику КР как ССНО в области сепаратрис представим моделью п-мерного тора. Приведенные на рис. 5 экспериментальные данные соответствуют модели (4) и тем полнее, чем длительней запись кардиоритма.
a
б
в
г
Рис. 5. Оценка ренормализационной инвариантности в спектрах кардиоинтервалограмм.
Спектры КИГ: а) - 10-ти-, б) - 4-х- и в) - 3-х-часовая запись; г - оценка скейлинга как отношения энергий при Фибоначчи-разбиении спектра КИГ.
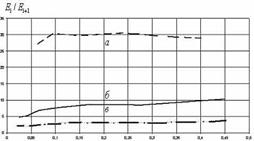
С позиций синергетики признаками для оценки состояния гомеостаза как системы определяющими параметрами КР являются фрактальная структура квазикристаллического типа с масштабно-инвариантным самоподобием (скейлингом) и спектр вида 1/f b.
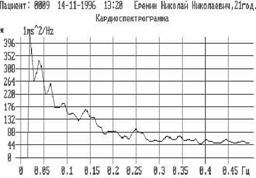
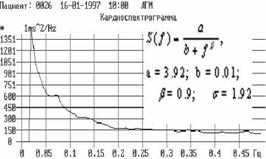
На рис. 6 приводятся сравнительные характеристики здорового пациента и больного инфарктом миокарда. Скелетоны вейвлет-преобразования, как картина линий локальных экстремумов поверхностей, выявляют структуру анализируемого процесса, а скейлинги – масштабную инвариантность или самоподобие Фрактальная размерность скелетонов вейвлет-преобразования деревьев Кейли D практически вырождается при патологии.
I
а Кардиоинтервалограмма в норме
б
D=4
D=3,58
D=2,62
D=3,631в
II
а Кардиоинтервалограмма при инфаркте миокарда
б
D=0
D=1
D=1
D=1в
Рис. 6. Кардиоинтервалограммы (а), вейвлет-анализ (б), скелетоны и их фрактальная
размерность (в) в норме (I) и при инфаркте миокарда (II)
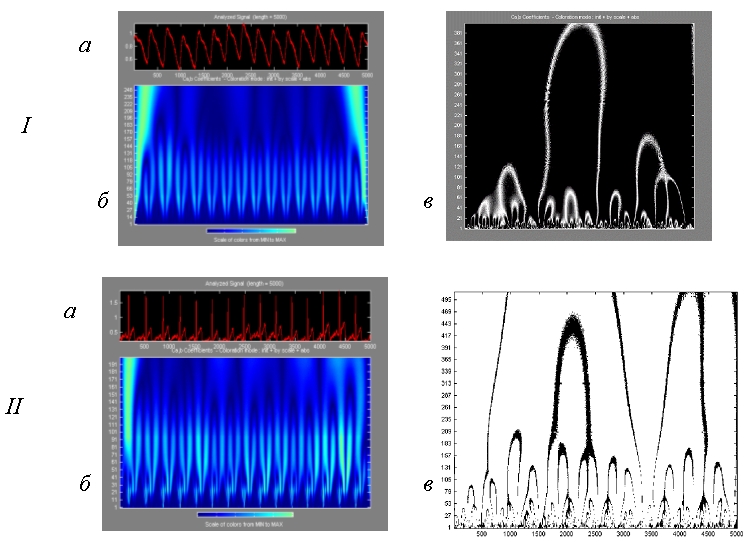
Такое же структурное самоподобие свойственно и биосигналам, отражающим морфологическое строение проводящих их сетей. На рис. 7 представлены вейвлет преобразования электрокардиосигналов (ЭКС) и пульсовых волн (ПВ). Скейлинги по узлам скелетонов ЭКС и ПВ (таблицы 1,2) показывают их близкое соответствие "золотому сечению" соотношения мод вейвлет-спектра.
Рис.7. I - ПВ (а), вейвлет-анализ ПВ (б), скелетон ПВ (в);II - электрокардиограмма (ЭКГ) (а), вейвлет-анализ ЭКГ (б), скелетон ЭКГ (в).
КАМ-теорема и модель ССНО объясняет механизмы и условия формирования фрактальных структур на основе n-мерного тора. Такой подход позволяет перейти от существующего в настоящее время феноменологического описания формирование спектральной характеристики вида 1/f, к четким физико-математическим моделям при анализе процессов и систем с самоорганизацией.
Список литературы:
Автор: Алдонин Геннадий Михайлович, профессор кафедры "Приборостроение" Красноярского государственного технического университета, e-mail: ald@rtf.kgtu.runnet.ru