УДК 538.566.2: 621.372.8
ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПЛАНАРНОМ ВОЛНОВОДЕ ИЗ МЕТАМАТЕРИАЛА С ПОТЕРЯМИ
А. А. Башарин, Н. Л. Меньших
Институт теоретической и прикладной электродинамики РАН,
Московский физико - технический институт
Получена 12 ноября 2010 г.
Аннотация. В работе представлены результаты расчетов дисперсионных характеристик планарного волновода из метаматериала с потерями, приведена классификация типов волн такого волновода. Показано, что в такой структуре могут существовать прямые и обратные волны, отмечена возможность распространения волн без затухания, несмотря на наличие потерь в метаматериале, а так же указано на наличие мод, распространяющихся с постоянной фазовой скоростью, независящей от частоты.
Ключевые слова: метаматериалы, планарный волновод.
Введение
Задачу поиска собственных волн открытого волновода обычно решают численными методами, ввиду сложности аналитических выводов. Простейший случай такой системы – планарный волновод. В работе [1] был предложен рекуррентный алгоритм, применимый для нахождения собственных волн, а так же был произведен расчет собственных волн для диэлектрического волновода с потерями. Однако, решений, удовлетворяющих дисперсионному уравнению, может оказаться довольно много, поэтому требуется не только найти собственные волны, но и уметь проанализировать результаты. Достаточно подробная классификация волн в открытых волноводах предложена в частности в работе [2].
В последние годы все больше внимания привлекают метаматериалы – т.е. вещества с одновременно отрицательными магнитной и диэлектрической проницаемостями. Уникальные свойства таких веществ были предсказаны В.Г.Веселаго в 1967г. [3]. С появлением первых образцов метаматериалов, в которых параметры были отрицательными для различных частотных диапазонов [4], а потом и в одном диапазоне частот [5,6] начинается бурное исследование их электродинамических характеристик. Была теоретически доказана [7] и экспериментально подтверждена [8] возможность преодоления дифракционного предела с помощью линзы из среды Веселаго. Другим важным направлением исследования стало излучение антенн на основе метаматериалов. В работе [9] изучаются свойства собственных волн двухслойного волновода, один слой которого имеет положительные проницаемости, а второй отрицательные. В [10] авторы, в частности, показали, что антенна на основе метаматериала, расположенного на металлической подложке, может иметь максимум излучения, как в прямом направлении, так и в обратном. Исследовались так же материалы со значением относительной диэлектрической проницаемости близкой к нулю. Так в работе [11] рассматривались свойства излучения вытекающих мод волновода из такого метаматериала. В [12] показано, что в планарном волноводе из метаматериала существуют прямые, обратные и стоячие волны. Излучение планарного волновода из метаматериала без потерь исследовалось в [13]. Авторами было показано, что антенна на основе такого материала может излучать в обратном направлении. Этот эффект был подтвержден экспериментально [14].
В данной работе исследованы дисперсионные характеристики планарного волновода из метаметериала с потерями, проанализировано влияние потерь на характеристики полей волновода, а так же проведена классификация типов волн.
Метод расчета
Рассмотрим планарный волновод из метаматериала (рис. 1).
Система представляет собой бесконечную пластину из метаматериала шириной 2а. Поля не зависят от координаты y. Относительные диэлектрическая и магнитная проницаемости волновода равны соответственно ε1 и µ1, а относительные проницаемости окружающего пространства – ε2 и µ2. Рассматриваемый метаматериал не идеальный и обладает потерями, поэтому его проницаемости являются комплексными величинами, т.е. имеют вид: ε1=ε1’+iε1’’, µ1=µ1’+iµ1’’.
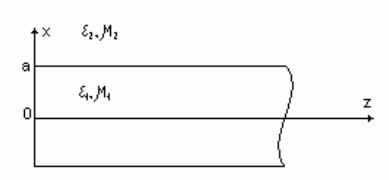
Рис. 1. Планарный волновод из метаматериала.
Поля в волноводе представим с помощью электрического вектора Герца. Для упрощения записи мы везде будем опускать временной множитель exp(-iωt). В случае четных ТМ-волн получаем:
![]() , |x|>a (1)
, |x|>a (1)
![]() , |x|<a
(2)
, |x|<a
(2)
где k1 и k2 – поперечные волновые числа в волноводе и в окружающем пространстве соответственно, и определяются следующим образом:
![]() (3)
(3)
![]() (4),
(4),
k0– волновое число в вакууме, h – продольное волновое число.
Используя граничные условия непрерывности тангенциальных компонент полей Ez и Hy, рассчитанных с помощью вектора Герца [15], на границе раздела двух сред (т.е. при x=a), получим дисперсионное уравнение для четных ТМ-волн:
![]() (5)
(5)
Подставив в уравнение (5) выражения (3) и (4) для k1 и k2 (условие непрерывности продольного волнового вектора h), приведем его к виду:
![]() (6)
(6)
Уравнение (6) решается методом Мюллера [16]. В качестве начальных приближений выбираются значения h в широком диапазоне: от 0 до нескольких k0.
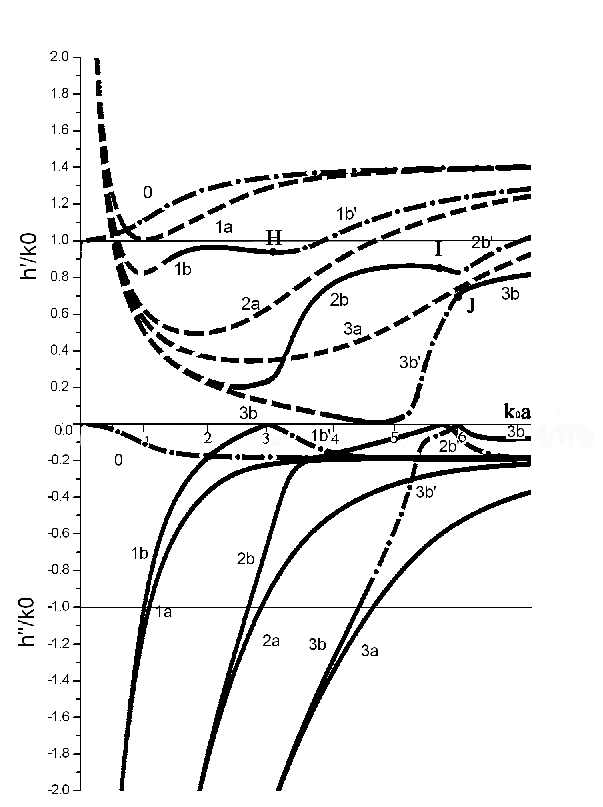
Для волновода из метаматериала с параметрами и ε’1=-2 и µ’1=-1 были произведены расчеты при различных мнимых частях проницаемостей. Результаты приведены в виде графиков зависимости h’/ k0 и h’’/ k0 от волнового числа свободного пространства k0a (рис. 2–7).
Большое количество волн, одновременно существующих в волноводе на данной частоте, заставляет уделить особое внимание их классификации.
Классификация волн
На графиках действительной и мнимой частей продольного волнового числа проведены прямые h’=k0 и h’’=k0, которые позволяют разделить волны на быстрые (h’<k0) и медленные (h’>k0), сильнозатухающие (h’’>k0) и слабозатухающие (h’’<k0) [17].
Рассмотрим случай, когда в метаматериале нет потерь. На низких частотах все волны являются обратными (пунктирные линии на графиках), т.е. направления фазовой скорости и вектора Пойтинга противоположны. На некоторой частоте (т. A, B на рис. 2) происходит расщепление волны на две моды: прямую (сплошные линии на графиках) и обратную.
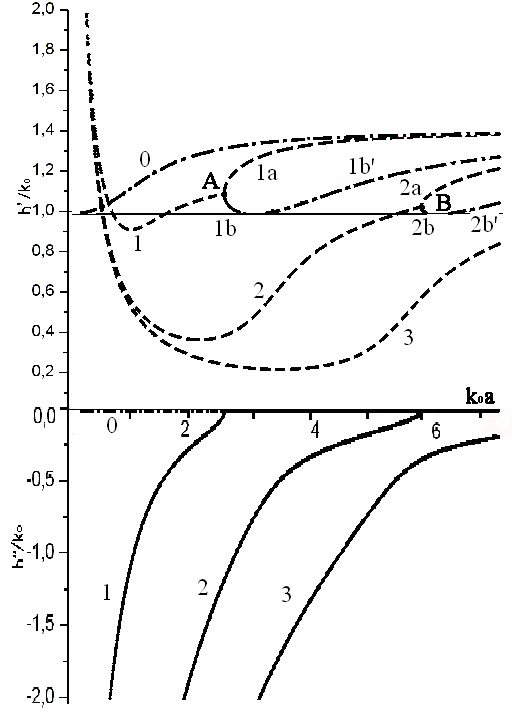
Рис. 2. Дисперсионная характеристика волновода с ε1=-2, µ1=-1
![]()
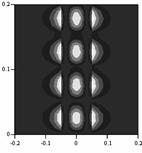
Поля этих волн представлены на рис. 8 и рис. 9. Обе моды начинают распространяться без потерь. При удалении от волновода поля спадают по экспоненциальному закону. Прямая волна существует только в небольшом частотном диапазоне. При дальнейшем увеличении частоты прямая волна переходит в антиповерхностную волну [16], которая имеет лишь математический смысл (штрихпунктирные линии на графиках).
Внутри волновода проекция вектора Пойтинга на ось z всегда отрицательна, а вне волновода – положительна. В точках расщепления (т. A, B на рис. 2) образуется нулевая плотность потока энергии, т.е. образуется стоячая волна, которая является интерференцией прямой и обратной волн, и проявляется эффект продольного резонанса [18,19].
При введении потерь расщепление происходит на низких частотах и во всем диапазоне существуют сразу обе моды (рис. 3). Одна мода остается обратной (рис. 3), а вторая на некоторой частоте превращается в прямую (т. P). Диапазон частот, в котором существуют прямые волны, увеличивается по сравнению со случаем без потерь.
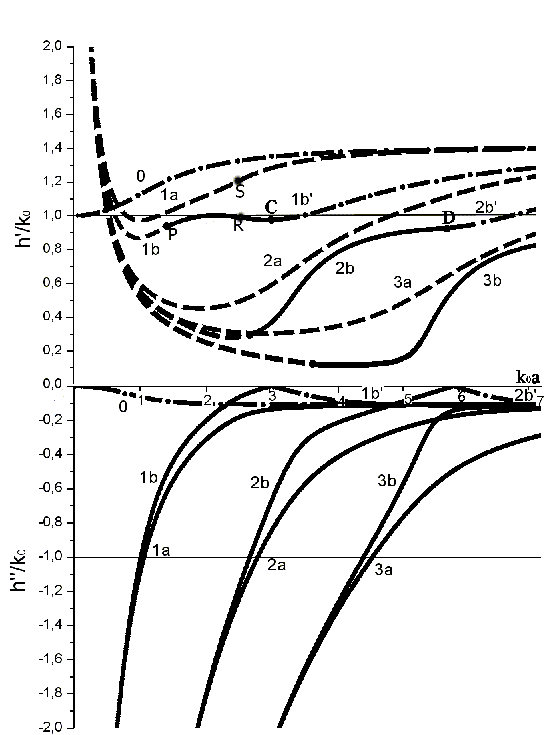
Рис. 3. Дисперсионная характеристика волновода с ε1=-2+i0.1, µ1=-1+i0.1
![]()
Поля этих волн становятся вытекающими (Рис. 10 а - прямая, б - обратная). Эти волны, как и в случае отсутствия потерь, с ростом частоты переходят в антиповерхностные. Однако, при достаточно больших потерях волна затухает, не достигнув точки перехода в прямую волну. В этом случае (рис. 6, т. T) обратная волна сразу превращается в антиповерхностную.
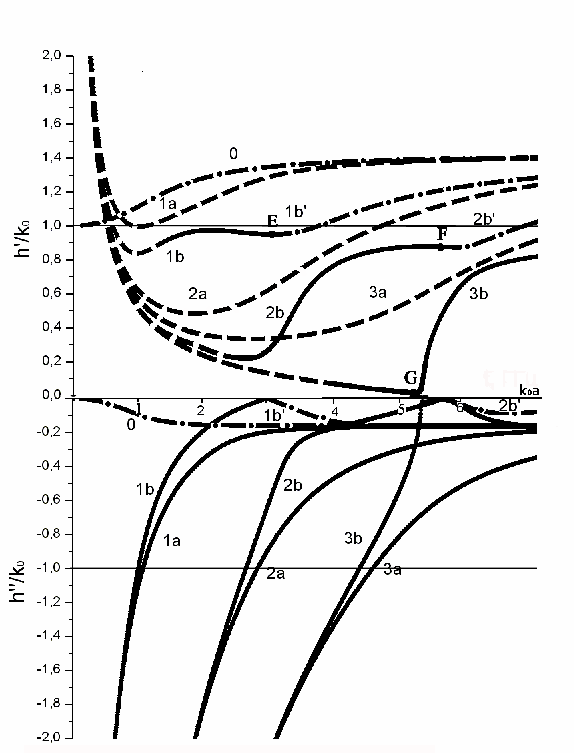
Рис. 4. Дисперсионная характеристика волновода с ε1=-2+i0.15, µ1=-1+i0.15
![]()
Некоторые результаты нуждаются в дополнительном обсуждении. При достаточно больших потерях (0.17 и более) для некоторых мод существует определенный диапазон частот, в котором прямая волна переходит в антиповерхностную. Так осуществляется переход моды 3b в 3b’ на рис. 5 и моды 2b в 2b’ на рис. 6.
Рис. 5. Дисперсионная характеристика волновода с ε1=-2+i0.17, µ1=-1+i0.17
![]()
Вблизи точки перехода поверхностной в антиповерхностную волну и наоборот, поле волны в основном сосредоточено в пространстве вне волновода. Даже при наличии потерь в метаматериале в таких точках волна может распространяться без потерь, т.е. мнимая часть продольного волнового вектора h’’ равно нулю (точки C,D,E,F,G,H,I,J,K,L,M,N).
При достаточно больших мнимых частях проницаемостей наблюдается объединение типов волн. Две прямые волны вначале объединяются антиповерхностной волной, которая с увеличением потерь исчезает. По графикам можно проследить объединение 2 и 3 мод (рис. 5), а при больших потерях, 1 и 2 (рис. 6,7).
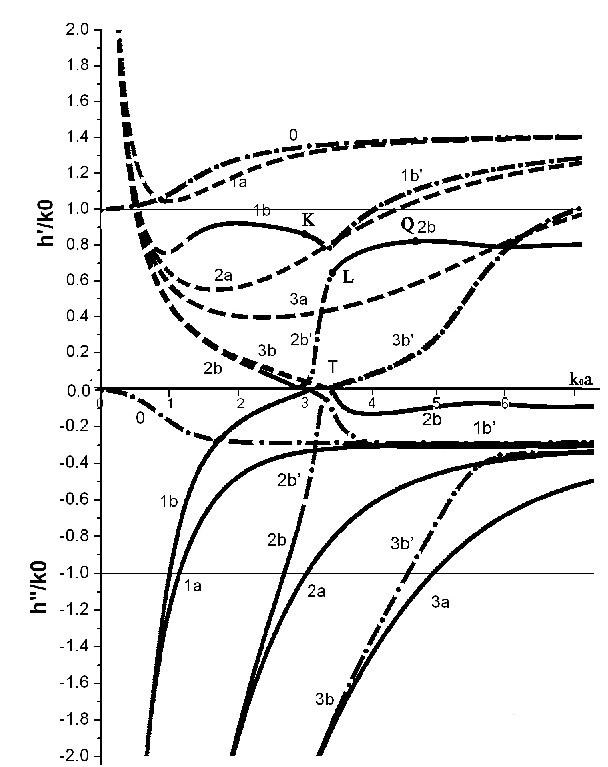
Рис. 6. Дисперсионная характеристика волновода с ε1=-2+i0.27, µ1=-1+i0.27
![]()
У этих волн, несмотря на наличие потерь в метаматериале (ε’’≠0, μ’’≠0), существуют точки (например, рис. 6, т. Q), в которых мнимая часть h близка к нулю. Поля этих волн сосредоточены вблизи границы метаматериал-окружающее пространство и в волновод практически не просачиваются (рис. 11).
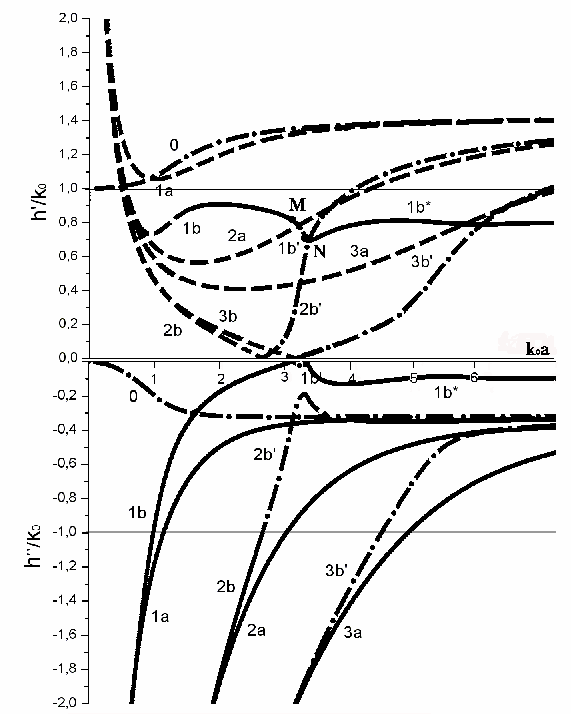
Рис. 7. Дисперсионная характеристика волновода с ε1=-2+i0.3, µ1=-1+i0.3.
![]()
С ростом частоты фазовая скорость обычно возрастает, начиная с некоторого момента, когда мнимая часть h становиться достаточно малой, чтобы эти волны могли распространяться.
Но для объединенных мод такой зависимости не наблюдается: фазовая скорость остается почти постоянной при увеличении частоты. Причем скорость становится постоянной при меньших потерях, т.е. до объединения волн у мод 3b на рис. 5 и 2b на рис. 6. Поля и потоки мощности таких волн в основном сосредотачиваются на границе волновода. Вне волновода поле так же спадает по экспоненте, кроме случаев, описанных выше (точки C,D,E,F,G,H,I,J,K,L,M,N).
Заключение
В работе исследованы математические модели типов волн планарного волновода из метаматериала с потерями, показано, что в такой структуре могут распространяться прямые и обратные волны. Указано на возможность распространения волн без затухания, т.е. с h’’≈0, на определенных частотах, несмотря на наличии потерь в метаматериале. При введении потерь наблюдается объединение типов волн, причем объединенные моды распространяются с постоянной фазовой скоростью, не зависящей от частоты. Эти волны являются прямыми, но в отличие от других прямых волн не вырождаются в антиповерхностные волны, а существуют во всем диапазоне частот, начиная с некоторой частоты. Их поля практически не просачиваются в волновод, сосредотачиваясь вблизи его границы.
Отметим, что реальные метаматериалы обладают сильной частотной дисперсией, потому создать материал с постоянными проницаемостями во всем рассматриваемом нами диапазоне частот не возможно. Но для каждого небольшого участка частот можно создать метаматериал с заданными проницаемостями, и в волноводе на его основе будут наблюдаться указанные выше свойства.
Авторы выражают благодарность В.В. Шевченко за полезные обсуждения.
Литература
1 Катин С.В., Титаренко А.А.// Антенны. 2006. выпуск 5 (108). С.24
2 Шевченко В.В.// Радиотехника и электроника. 1969. Т.10. С.1768.
3 Веселаго В.Г.// Успехи физ. наук. 1967. Т.92. С.517.
4 Lagarkov A.N., Semenenko V.N., Chistyaev V.A. et al.// Electromagnetics. 1997. V.17. P. № 3.213
5 Lagarkov A.N., Semenenko V. N., Kisel V. N., and Chistyaev V. A., J. Magn. Magn. Mater. 258–259, 161(2003).
6 Smith D.R., Padilla W.T., Vier D.C. et al.// Phys. Rev. 2000. V. 84. P. 584.
7 Pendry J.B.// Phys. Rev. Lett. 2000. V.85. №18. P.3966
8 Lagarkov A.N., Kissel V.N.//Phys. Rev. Lett..2004. V.92. №92. P.077401.
9 Nefedov I.S., Tretyakov S.A.// Radio Science 2003. V. 38. №6. P. 1101.
10 Caloz C., Itoh T. Electromagnetic metamaterials: transmission line theory and microwave applications. N.Y.: John Wiley and Sons, Inc., 2006.
11 Alu A., Bilotti F., Engheta N., Vegni L.//IEEE Trans. 2007. V. AP-55. №6 Pt 2. P. 1698.
12 Шевченко В.В. //Радиотехника и электроника. 2005. Т. 50. №11. С. 1363.
13 Балабуха Н.П., Башарин А.А., Семененко В.Н.// Радиотехника и электроника. 2009. V. 54. №8. С. 946.
14 Балабуха Н.П., Башарин А.А., Семененко В.Н.// Письма в ЖЭТФ. Т.89, №10. 2009.
15 Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979
16 Muller D.E.// Mathematical Tables and Aids to Computation. 1965. T.10. P.208.
17 Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
18 Шатров А.Д., Шевченко В.В.// Известия ВУЗов. Радиофизика. 1974. Т. 17. №11. С.1692.
19 Шевченко В.В. //Радиотехника и электроника. 2000. Т. 45. №10. С. 1157.