УДК 537.8
векторное Интегральное представление нестационарного электромагнитного поля в проводящей среде
А.
С. Ильинский, И.
Г. Ефимова
Московский государственный университет им. М. В. Ломоносова
Получена 24 ноября 2010 г.
Аннотация. Векторы напряженностей нестационарного электромагнитного поля в однородной изотропной проводящей среде представлены во временной области в интегральной форме.
Ключевые слова: нестационарное электромагнитное поле, проводящая среда, интегральное представление.
В соответствии с известной теоремой эквивалентности монохроматическое электромагнитное поле в однородной изотропной среде может быть выражено в интегральной форме через значения векторов напряженностей электрического и магнитного полей на замкнутой поверхности [1-4]. Интегральные представления в частотной области для напряженностей электрического и магнитного полей, называемые формулами Стрэттона-Чу и справедливые при любых значениях материальных параметров среды, были получены и подробно проанализированы в [1, 4]. Эти представления широко используются для составления частотных интегральных уравнений, которые применяются для решения разнообразных электродинамических задач [2, 4-7].
Во временной области электромагнитное поле, существующее в непроводящей среде, также может быть представлено в интегральной форме через значения напряженностей электрического и магнитного полей на замкнутой поверхности. В этом случае напряженности полей, входящие в подынтегральные выражения, являются функциями от запаздывающего временного аргумента. Такое представление было получено в скалярной [1] и векторной [2] формах и успешно применяется для составления временных интегральных уравнений, используемых в численных исследованиях рассеяния нестационарного электромагнитного поля на идеально проводящих телах и диэлектрических телах без потерь, расположенных в непроводящей среде [2, 8, 9]. Вопросы существования и единственности решения временных интегральных уравнений для тока, наведенного на поверхности идеально проводящего рассеивателя, рассматривались в [10, 11]. Однако к настоящему времени метод временных интегральных уравнений не был разработан для случая проводящей среды, поскольку не было получено интегральное представление нестационарного электромагнитного поля в такой среде. В книге [1] отмечено, что при применении метода Кирхгофа интегрирования неоднородного волнового уравнения наличие проводимости среды приводит к значительным аналитическим трудностям.
Целью настоящей работы является получение временного интегрального представления нестационарного электромагнитного поля в однородной изотропной среде, обладающей проводимостью.
Будем рассматривать однородную изотропную среду с материальными параметрами, не зависящими ни от времени ни от пространственных координат. В этом случае уравнения Максвелла имеют вид
где ![]() и
и ![]() -
векторы
напряженностей
электрического
и магнитного
полей, соответственно,
-
векторы
напряженностей
электрического
и магнитного
полей, соответственно,
![]() - диэлектрическая
проницаемость,
- диэлектрическая
проницаемость, ![]() - магнитная
проницаемость,
- магнитная
проницаемость, ![]() -
удельная
электрическая
проводимость,
-
удельная
электрическая
проводимость,
![]() - удельная
магнитная
проводимость,
- удельная
магнитная
проводимость,
![]() и
и ![]() - объемные
плотности сторонних
электрического
и магнитного
токов,
соответственно.
Предполагается,
что
- объемные
плотности сторонних
электрического
и магнитного
токов,
соответственно.
Предполагается,
что ![]() ,
,
![]() ,
, ![]() и
и ![]() являются
постоянными
величинами, а
являются
постоянными
величинами, а
![]() и
и ![]() конечными
функциями
непрерывными
вместе со
всеми своими
производными
во всех обыкновенных
точках
пространства
(в которых нет
резких
изменений
физических
свойств среды).
конечными
функциями
непрерывными
вместе со
всеми своими
производными
во всех обыкновенных
точках
пространства
(в которых нет
резких
изменений
физических
свойств среды).
Считаем, что сторонние токи и заряды удовлетворяют уравнениям непрерывности
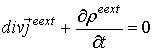 ,
,
где ![]() и
и ![]() объемные
плотности
электрического
и магнитного
зарядов,
соответственно.
Также мы
предполагаем,
что все
функции времени,
рассматриваемые
в данной
задаче, - напряженности
электрического
и магнитного полей,
объемные
плотности сторонних
токов и зарядов
- равны нулю
вместе со
своими
производными
до момента
времени
объемные
плотности
электрического
и магнитного
зарядов,
соответственно.
Также мы
предполагаем,
что все
функции времени,
рассматриваемые
в данной
задаче, - напряженности
электрического
и магнитного полей,
объемные
плотности сторонних
токов и зарядов
- равны нулю
вместе со
своими
производными
до момента
времени ![]() включительно.
включительно.
Из уравнений Максвелла (1) и уравнений непрерывности (2) можно получить соотношения
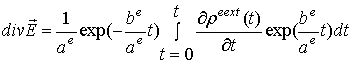 ,
,
где
Уравнения
(1) и (3)
составляют
полную
систему
уравнений,
описывающих
электромагнитное
поле в однородной
изотропной
среде.
Запишем
векторные
волновые
уравнения
для ![]() и
и![]() .
Имеем из
первого и
второго
уравнений
Максвелла
.
Имеем из
первого и
второго
уравнений
Максвелла
и
соответственно. Перепишем волновые уравнения (5) и (6) в виде
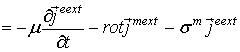 , (7)
, (7)
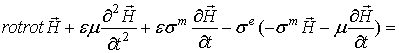
Далее
проведем
выкладки
только для
поля ![]() , а
затем
перейдем к
результату
для поля
, а
затем
перейдем к
результату
для поля ![]() по
принципу
двойственности
[3]. В силу
векторного
тождества
по
принципу
двойственности
[3]. В силу
векторного
тождества
![]()
уравнение (7) можно представить в виде
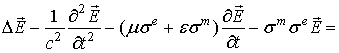
где 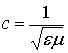 -
скорость
света.
-
скорость
света.
Введем обозначения
Тогда волновое уравнение в формах (7) и (9) можно записать в виде
соответственно. Волновое уравнение можно упростить, избавившись от первой производной поля по времени с помощью замены
Кроме того, в уравнении (7) введем замены
![]() ,
,
Вычислив первую и вторую производные поля по времени
и учитывая замены (13) и (14), преобразуем уравнение (7) к виду
Для
получения
интегрального
представления
напряженности
нестационарного
электрического
поля,
удовлетворяющего
волновому
уравнению (15),
мы применим
методику из
книги [1] и
будем использовать
векторный
аналог
теоремы
Грина. Пусть ![]() замкнутая
область
пространства,
ограниченная
регулярной
(удовлетворяющей
условиям
Ляпунова)
поверхностью
замкнутая
область
пространства,
ограниченная
регулярной
(удовлетворяющей
условиям
Ляпунова)
поверхностью
![]() ,
, ![]() и
и ![]() векторные
функции
точки, непрерывные
в области
векторные
функции
точки, непрерывные
в области ![]() и на
поверхности
и на
поверхности ![]() вместе
со своими
первыми и
вторыми
производными.
Тогда, как
показано в [1],
имеет место
векторный
аналог
теоремы Грина
вместе
со своими
первыми и
вторыми
производными.
Тогда, как
показано в [1],
имеет место
векторный
аналог
теоремы Грина
где ![]() -
внешняя
нормаль к
поверхности
-
внешняя
нормаль к
поверхности ![]() . Положим
в (16)
. Положим
в (16)
где ![]() постоянный
единичный
вектор
произвольного
направления. С
использованием
формул
векторного
анализа получаем
левую часть (16)
в виде
постоянный
единичный
вектор
произвольного
направления. С
использованием
формул
векторного
анализа получаем
левую часть (16)
в виде
![]()
Так
как ![]() = const и
= const и
![]() ,
,
имеем
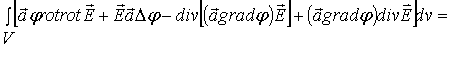
Здесь постоянный
вектор ![]() вынесен
за знак
интеграла
как общий
множитель
подынтегральных
слагаемых.
вынесен
за знак
интеграла
как общий
множитель
подынтегральных
слагаемых.
Теперь
вычислим
правую часть (16)
и с помощью
формул
векторного
анализа преобразуем
входящие в
нее
подынтегральные
слагаемые так,
чтобы вектор ![]() являлся
их общим
множителем. В
результате
имеем
являлся
их общим
множителем. В
результате
имеем
![]()
где
вектор ![]() вынесен
за знак
интеграла,
как
постоянный коэффициент,
являющийся
общим
множителем
подынтегральных
слагаемых.
вынесен
за знак
интеграла,
как
постоянный коэффициент,
являющийся
общим
множителем
подынтегральных
слагаемых.
Приравнивая выражения (19) и (20), получим (16) в виде
![]()
Вводя замену
и
подставляя
выражение
для ![]() из
(15) в (21) с учетом (13)
и (14), получим
из
(15) в (21) с учетом (13)
и (14), получим
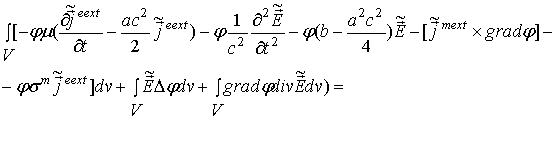
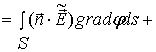
Здесь учтены равенства
и
а также тождество
которое следует из формул векторного анализа
и
В
формуле (23)
обозначим
объемный и
поверхностный
интегралы ![]() и
и ![]() ,
соответственно,
т.е.,
,
соответственно,
т.е.,
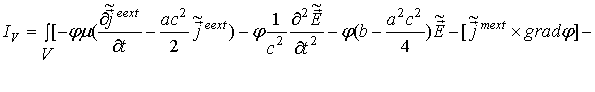
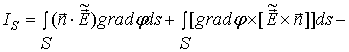
Выберем
в качестве ![]() решение
скалярного
однородного
волнового
уравнения
для непроводящей
среды
решение
скалярного
однородного
волнового
уравнения
для непроводящей
среды
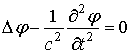
и
вычислим
сумму 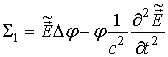 . Имеем
. Имеем
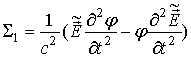 .
.
Прямая проверка показывает, что
С
учетом
равенства (31) получим
выражение
для
объемного
интеграла ![]() :
:
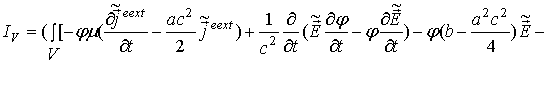
Следуя методике [1], положим
где ![]() ,
, ![]() -
декартовы
координаты
точки
наблюдения,
-
декартовы
координаты
точки
наблюдения, ![]() -
декартовы
координаты
точки
интегрирования
в формуле (16),
-
декартовы
координаты
точки
интегрирования
в формуле (16), ![]() , а
, а ![]() - некоторый
постоянный
малый
параметр,
который в
дальнейшем будет
устремлен к
нулю.
- некоторый
постоянный
малый
параметр,
который в
дальнейшем будет
устремлен к
нулю.
Мы рассматриваем непрерывные функции [12] такие, для которых
и
При ![]() функция
функция
![]() превращается
в
превращается
в ![]() -функцию.
Нормировка
-функцию.
Нормировка ![]() такова,
что
такова,
что
Для
того, чтобы
иметь дело с
функцией,
которая
непрерывна
со своими
производными,
пока мы не
будем
переходить к
пределу при ![]() . (В
дальнейшем
мы
проинтегрируем
левую и правую
части
равенства (23)
по времени от
. (В
дальнейшем
мы
проинтегрируем
левую и правую
части
равенства (23)
по времени от
![]() до
до
![]() и
перейдем к
пределу при
и
перейдем к
пределу при ![]() .)
.)
Подставим
выражение (33)
для ![]() в
объемный
интеграл (32),
учтем, что
в
объемный
интеграл (32),
учтем, что
где ![]() - это
единичный
вектор,
направленный
от точки
интегрирования
- это
единичный
вектор,
направленный
от точки
интегрирования
![]() к
точке
наблюдения
к
точке
наблюдения ![]() ,
,
и
проинтегрируем
результат по
времени от ![]() до
до ![]() . В
результате получим
. В
результате получим
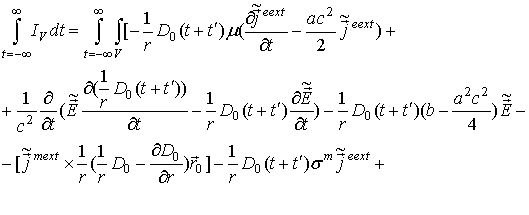
В силу (34) можно поменять порядок интегрирования в (39). Учитывая, что
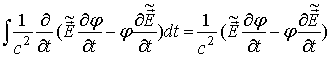 ,
,
и что,
в
соответствии
с (33), ![]() при
при
![]() и
и ![]() ,
имеем
,
имеем
В (39)
перейдем к
пределу при ![]() и
учтем (40):
и
учтем (40):
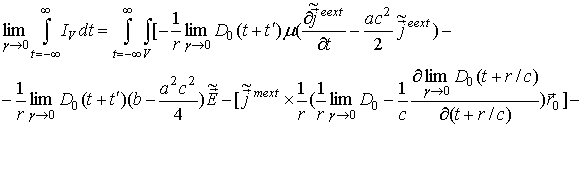
Так как
то с
учетом
свойств ![]() -функции
[12]
-функции
[12]
и
мы получаем из (41)
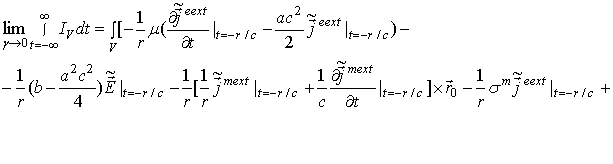
Теперь рассмотрим поверхностный интеграл в (23) с учетом замен (13), (14) и (22):
Функция
![]() имеет
особенность
в точке
имеет
особенность
в точке ![]() . Следуя
методике [1],
окружим эту
точку сферой
. Следуя
методике [1],
окружим эту
точку сферой ![]() малого
радиуса
малого
радиуса ![]() с
центром в точке
наблюдения
с
центром в точке
наблюдения ![]() ,
исключив тем
самым эту
точку из
области
,
исключив тем
самым эту
точку из
области ![]() . Имеем
. Имеем
где ![]() - это
внешняя
поверхность,
ограничивающая
объем
- это
внешняя
поверхность,
ограничивающая
объем ![]() ,
,
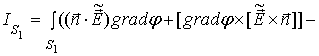
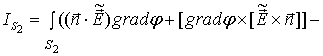
Рассмотрим
первый из
поверхностных
интегралов и
вычислим
сумму двух
первых слагаемых
подынтегрального
выражения.
Напомним, что
![]() -
это внешняя
нормаль к
поверхности,
ограничивающей
объем
-
это внешняя
нормаль к
поверхности,
ограничивающей
объем ![]() , а
единичный
вектор
, а
единичный
вектор ![]() направлен
к точке
наблюдения
направлен
к точке
наблюдения ![]() . На
поверхности
. На
поверхности ![]() имеем
имеем
![]() . Представив
выражение
для
. Представив
выражение
для ![]() (37)
в виде
(37)
в виде
имеем
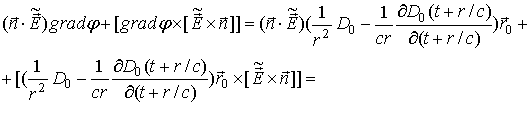
Так как
![]() ,
,
то
и, следовательно,
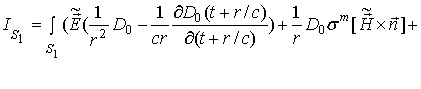
Теперь
проинтегрируем
выражение (52)
от ![]() до
до
![]() и
перейдем к
пределу при
и
перейдем к
пределу при ![]() ,
учитывая
свойства
рассматриваемых
функций (34) и (35) и
свойства
,
учитывая
свойства
рассматриваемых
функций (34) и (35) и
свойства ![]() -функции
(43) и (44):
-функции
(43) и (44):
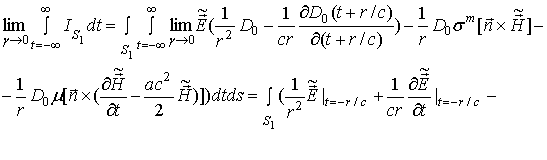
Далее,
устремляя
радиус
маленькой
сферы ![]() к нулю,
к нулю, ![]() ,
получим
,
получим
Рассмотрим
интеграл по
внешней
поверхности ![]() ,
выраженный
соотношением
(49):
,
выраженный
соотношением
(49):
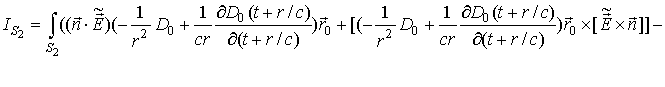
На
поверхности ![]() вектор
вектор
![]() направлен
к точке
наблюдения,
т.е., внутрь
направлен
к точке
наблюдения,
т.е., внутрь ![]() .
.
Далее
проинтегрируем
выражение (56)
от ![]() до
до
![]() и
перейдем к
пределу при
и
перейдем к
пределу при ![]() ,
учитывая
свойства
рассматриваемых
функций (34) и (35) и
свойства
,
учитывая
свойства
рассматриваемых
функций (34) и (35) и
свойства ![]() -функции
(43) и (44):
-функции
(43) и (44):
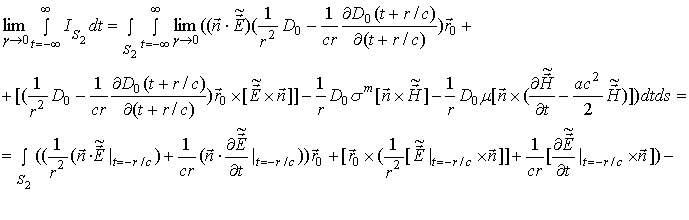
Используя равенство
и соотношения (23), (45), (47), (55), (57) и (58), получим
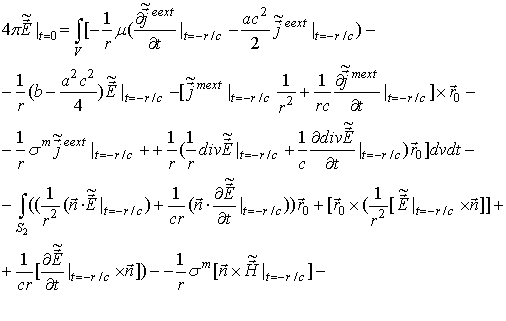
Повторяя
рассуждение [1]
о том, что момент
наблюдения ![]() выбран
произвольно,
можно
переписать (59)
в виде
выбран
произвольно,
можно
переписать (59)
в виде
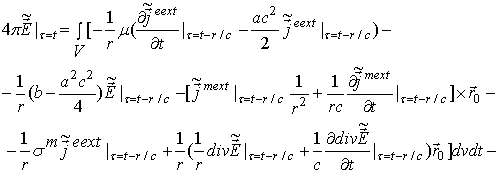
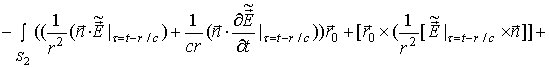
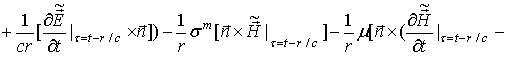
Формулу
(60) можно
получить и
формально.
Для этого
нужно везде
сделать
замену ![]() и в
формуле (33)
положить
и в
формуле (33)
положить ![]() .
.
Применив принцип двойственности [3] к (60), получаем интегральное представление для вектора напряженности нестационарного магнитного поля
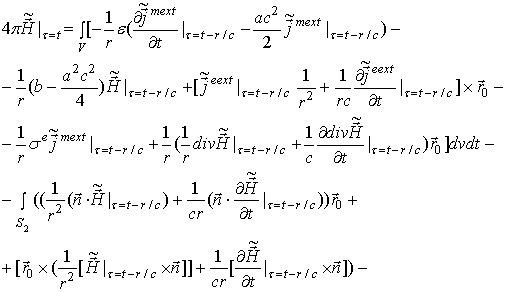
В
случае, когда
все функции
зависят от
времени как ![]() и
и ![]() ,
формулы (60) и (61)
переходят в
интегральные
представления
[1, раздел 8.14, с. 410,
формулы (19), (20)]
известные
как формулы
Стрэттона-Чу.
,
формулы (60) и (61)
переходят в
интегральные
представления
[1, раздел 8.14, с. 410,
формулы (19), (20)]
известные
как формулы
Стрэттона-Чу.
Таким образом, получены интегральные представления для векторов напряженностей нестационарных электрического и магнитного полей в однородной изотропной проводящей среде. В соответствии с полученными соотношениями, поле в любой момент времени в произвольной точке внутри некоторого объема выражается через интеграл по поверхности, ограничивающей данный объем, и интеграл по объему. Подынтегральные функции содержат значения напряженностей полей, сторонних токов и зарядов, а также производных этих величин по времени в моменты, предшествующие моменту наблюдения.
ЛИТЕРАТУРA
1. Стрэттон Дж. А. Теория электромагнетизма. М.-Л.: ГИТТЛ, 1948.
2. Вычислительные методы в электродинамике /Под ред. Р. Митры. М.: Мир, 1977.
3. Марков Г. Т., Чаплин А. Ф. Возбуждение электромагнитных волн. М: Радио и связь, 1983.
4. Дмитриев В. И., Захаров Е. В. Интегральные уравнения в краевых задачах электродинамики. М.: Издательство Московского университета, 1987.
5. Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. М.: Мир, 1987.
6. Васильев Е. Н. Возбуждение тел вращения. М.: Радио и связь, 1987.
7. Ильинский А. С., Слепян Г. Я. Колебания и волны в электродинамических системах с потерями. М.: Издательство Московского университета, 1983.
8. Transient Electromagnetic Fields/ Ed. by L. B. Felsen (Topics in Applied Physics, V. 10). New York: Springer--Verlag, 1977.
9. Васильев Е. Н., Ефимова, И.Г.// Известия вузов. Радиофизика. 1984. Т. 27. №1. С.87--95.
10. Кравцов В. В.// Вычислительные методы и программированию. Сб. работ Вычислительного центра МГУ. Вып. 5. 1966. С. 260.
11. Ефимова И. Г.// Радиотехника и электроника. 2008. Т. 53. №12. С. 1486-1488.
12. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1973.
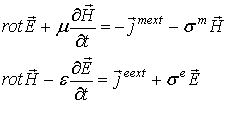 , (1)
, (1)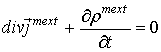 , (2)
, (2)
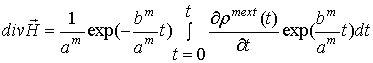 , (3)
, (3)
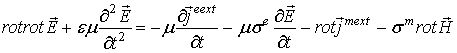 (5)
(5)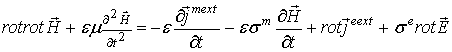
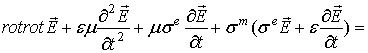
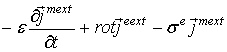 . (8)
. (8)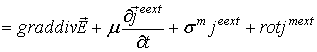 ,
, 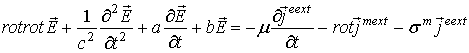 , (11)
, (11) 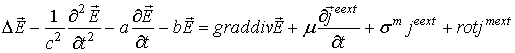 , (12)
, (12)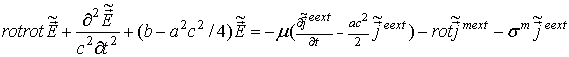 . (15)
. (15)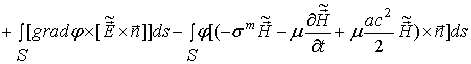 .
. 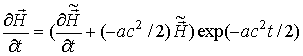 ,
, 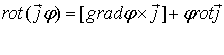
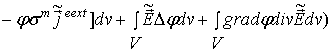 ,
, 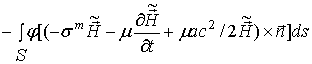 . (30)
. (30)
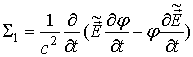 . (31)
. (31)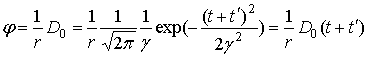 , (33)
, (33)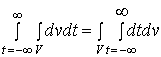 (34)
(34)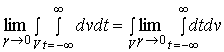 . (35)
. (35)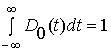 . (36)
. (36)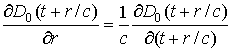 , (38)
, (38)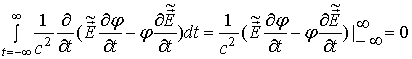 . (40)
. (40)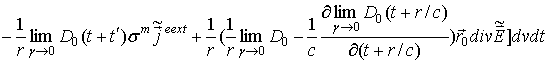 .
. 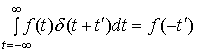 (43)
(43)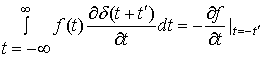 , (44)
, (44)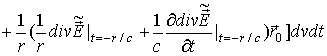 .
(45)
.
(45)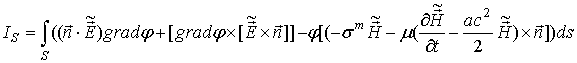 . (46)
. (46)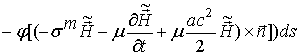 ,
(48
,
(48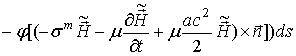 .
. 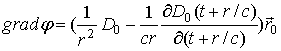 ,
, 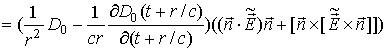 .
. 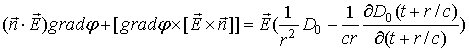
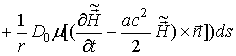 . (53)
. (53)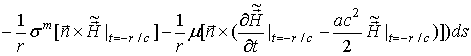 . (54)
. (54)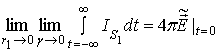 . (55)
. (55)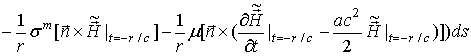 . (57)
. (57)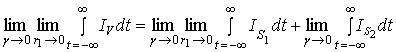
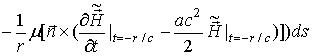 . (59)
. (59)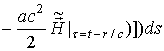 .
. 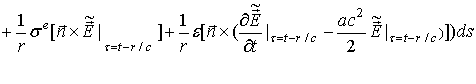 . (61)
. (61)