УДК 537.311.322
квантовохимическое Моделирование структуры кремниевых фуллеренов
В. В. Филиппов, А Н. Власов
Липецкий государственный педагогический университет, кафедра физики
Получена 10 ноября 2011 г.
Аннотация. Представлены результаты оптимизации атомной и электронной структуры кластеров кремния со структурой подобной углеродным фуллеренам. Определены основные квантово-энергетические параметры, характеризующие электронные свойства исследуемых наноформ. Для исследования устойчивости кремниевых фуллеренов определены энергии связей гидрированных и инкапсулированных атомами металлов наноструктур.
Ключевые слова: кремний, наночастица, фуллерен, NDDO PM3.
Abstract. The results of optimization of the atomic and electronic structure of silicon clusters with a structure similar to carbon fullerenes. Determined the basic quantum-energy parameters characterizing the electronic properties of the investigated nano-forms. To investigate the stability of silicone fullerenes determine the binding energy of the hydrogenated and the encapsulated metal atoms nanostructures.
Keywords: silicon, nanoparticles, fullerenes, NDDO PM3.
Введение
Известно, что одним из перспективных классов материалов нанотехнологий являются фуллерены [1]. После открытия фуллерена С60 в 1985 г. [2] начали появляться обоснованные предположения, что кремний и германий также могут образовывать энергетически устойчивые сфероидальные геометрические структуры. Относительно недавно японские ученые сообщили о том, что им удалось получить устойчивые кластеры из 12 и 18 атомов кремния с замкнутой структурой [3]. Стабилизации кремниевых наноструктур удавалось добиться путем помещения внутрь сфероидальной наночастицы атома переходного металла. Структура полученных кластеров представляла собой шестиугольную призму или икосаэдр в случае кластера МеSi12 , в случае кластера Me2Si18 – две шестиугольные призмы с общим основанием.
Необходимо отметить, что кремний является самым распространенным материалом современной электроники. Естественно полагать, что различные наноформы кремния можно использовать в качестве структурных элементов наноэлектронных транзисторов, выпрямляющих элементов, а также одноэлектронных приборов. Соответственно, у инженеров и ученых наблюдается особый интерес, направленный на экспериментальные исследования кремниевых кластеров [4-6], а также на теоретическое моделирование известных кластеров и прогнозирование их свойств [7-10]. В настоящее время уже получены устойчивые модификации некоторых кремниевых кластеров [4-6], а также фуллереноподобные структуры [11-13], кремниевые нанотрубки [14, 15] и однослойные пленки силицена [16]. Однако, физико-химические свойства указанных кремниевых наноформ исследованы не достаточно.
В данной работе представлены результаты оптимизации атомной и электронной структуры кластеров кремния со структурой подобной углеродным фуллеренам. Определены основные квантово-энергетические параметры, характеризующие электронные свойства исследуемых наноформ.
Методика расчета
В качестве расчетных методов выбраны метод силового поля ММ+ (для оптимизации структуры остова) [17] и квантовохимический метод NDDO РМ3-UHF (для расчета электронных свойств) [18, 19]. Выбор именно данных методов обусловлен хорошей степенью их надежности и воспроизводимости результатов [20-24]. Для исследования устойчивости кремниевых фуллеренов определены также энергии связей гидрированных и инкапсулированных структур атомами переходных металлов. Во всех рассмотренных ниже случаях мультиплетность структуры определялась как минимальная, поскольку в приведенных выше экспериментальных работах по кремниевым наноформам не отмечалось о проявлении ими каких-либо магнитных свойств.
В методе силового поля
ММ+ энергии заряд диполь и диполь-диполь оцениваются с точностью до членов ![]() . Вычисление
потенциальной энергии растяжения валентных связей в ММ+ использует разложение
до кубического члена:
. Вычисление
потенциальной энергии растяжения валентных связей в ММ+ использует разложение
до кубического члена:
![]() . (1)
. (1)
Энергия деформации валентных углов вычисляется в ММ+ с включением члена шестого порядка:
![]() . (2)
. (2)
Поправка, учитывающая изменение связи при изменении валентного угла вычисляется виде суммы по всем связям и валентным углам по формуле:
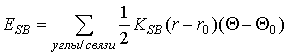 . (3)
. (3)
Поправка, учитывающая внеплоскостные деформации вычисляется в виде суммы по всем группам атомов, образующих тригональную плоскую структуру по формуле:
![]() . (4)
. (4)
Видно, что для каждого угла функция энергии аналогична функции изгиба валентных углов, но в качестве независимой переменной в данном случае используется угол, образуемый связью с плоскостью, в которой расположены атомы в недеформированном состоянии.
Энергия ван-дер-ваальсовых взаимодействий, описывающая притяжение атомов на больших расстояниях и отталкивание на близких в ММ+ определяется выражением:
![]() , (5)
, (5)
где ![]() , а
, а ![]() и
и ![]() – значения ван-дер-ваальсовых радиусов, а
суммирование производится по всем валентно не связанным атомам.
– значения ван-дер-ваальсовых радиусов, а
суммирование производится по всем валентно не связанным атомам.
В указанных выше
выражениях константы ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ‑ экспериментальные параметры,
определяемые с точностью до постоянного множителя, зависящего от выбора системы
единиц.
‑ экспериментальные параметры,
определяемые с точностью до постоянного множителя, зависящего от выбора системы
единиц.
В методе РМ3 полная энергия кластера вычисляется следующим образом:
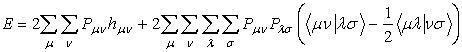 , (6)
, (6)
![]() , (7)
, (7)
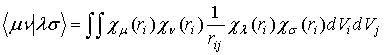 , (8)
, (8)
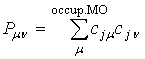 . (9)
. (9)
Здесь ![]() – матрица электронной плотности,
– матрица электронной плотности, ![]() – оператор кинетической
энергии электрона и энергии его притяжения к ядрам.
– оператор кинетической
энергии электрона и энергии его притяжения к ядрам.
Заряд на атомах определялся по методу Малликена:
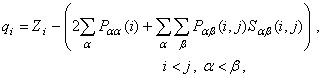 (10)
(10)
где ![]() – заряд ядра атома
– заряд ядра атома ![]() ,
, ![]() – электронная заселенность орбитали
– электронная заселенность орбитали ![]() на атоме
на атоме ![]() ,
, ![]() – интеграл перекрывания
орбиталей
– интеграл перекрывания
орбиталей ![]() и
и ![]() атомов
атомов ![]() и
и ![]() ,
, ![]() – половина от электронной заселенности
перекрывания орбиталей
– половина от электронной заселенности
перекрывания орбиталей ![]() и
и ![]() атомов
атомов ![]() и
и ![]() .
.
Результаты расчетов
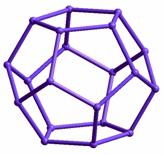
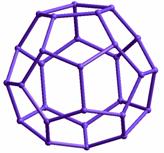
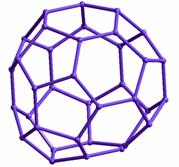
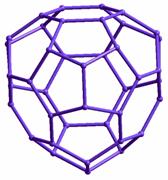
В приведенной таблице 1 представлены геометрические структуры оптимизированных методом ММ+ некоторых кремниевых фуллеренов, указаны классы симметрии структур, а также рассчитанные средние длины связей. В таблице 2 отражены результаты квановохимических расчетов энергетических параметров исследуемых структур.
Таблица 1. Атомная структура оптимизированных кремниевых фуллеренов.
|
Si20 , cимм. – С1, <а>=2.35 |
Si28, cимм. – С1, <а>=2.34 |
|
|
|
|
Si36, cимм. – С2, <а>=2.33 |
Si40, cимм. – С1, <а>=2.34 |
|
|
|
|
Si50, cимм. – D5H, <а>=2.33 |
Si60, cимм. – СI, <а>=2.34 |
|
|
|
Таблица 2. Рассчитанные квантово-энергетические параметры кремниевых фуллеренов.
|
Структура |
2S+1 |
Есвязи, eV |
Есвязи/ат., eV |
ЕHOMO, eV |
DЕ, eV |
qMe, e |
|
Si20 |
1 |
-77.23 |
-3.86 |
-7.46 |
2.66 |
- |
|
H20Si20 |
1 |
-143.29 |
-3.58 |
-9.18 |
6.71 |
- |
|
CuSi20 |
2 |
-90.94 |
-4.33 |
-7.90 |
3.26 |
+0.2 |
|
CaSi20 |
1 |
-110.40 |
-5.26 |
-7.71 |
3.11 |
-0.46 |
|
Si28 |
1 |
-114.65 |
-4.09 |
-7.96 |
3.72 |
- |
|
H28Si28 |
1 |
-199.03 |
-3.55 |
-8.80 |
6.21 |
- |
|
CuSi28 |
2 |
-120.91 |
-4.17 |
-7.55 |
3.04 |
+0.56 |
|
CaSi28 |
1 |
-141.79 |
-4.89 |
-7.51 |
3.03 |
-0.05 |
|
Si36 |
1 |
-149.56 |
-4.15 |
-7.97 |
3.72 |
- |
|
H36Si36 |
1 |
-254.06 |
-3.53 |
-8.75 |
6.07 |
- |
|
CuSi36 |
2 |
-154.97 |
-4.18 |
-8.00 |
3.8 |
-0.03 |
|
CaSi36 |
1 |
-170.72 |
-4.62 |
-7.62 |
3.00 |
+0.2 |
|
Si40 |
1 |
-166.18 |
-4.15 |
-8.03 |
3.82 |
- |
|
H40Si40 |
1 |
-281.70 |
-3.52 |
-8.59 |
5.89 |
- |
|
Si50 |
1 |
-209.94 |
-4.20 |
-7.67 |
3.06 |
- |
|
H50Si50 |
1 |
-350.08 |
-3.50 |
-8.57 |
5.79 |
- |
|
Si60 |
1 |
-255.25 |
-4.25 |
7.98 |
3.88 |
- |
|
H60Si60 |
1 |
-427.00 |
-3.56 |
8.57 |
5.73 |
- |
Выводы и результаты
Выполненные расчеты по оптимизации атомной структуры кремниевых фуллеренов и определению квантово-энергетических параметров позволяют сделать следующие нижеуказанные выводы.
Атомный остов составлен на основе пятиугольников и шестиугольников с типом связи sp2, не характерным для кристаллических кремниевых структур. Среднее межатомное расстояние кремниевых фуллеренов примерно соответствует длине связи в кристаллическом кремнии.
Все представленные наноструктуры являются энергетически устойчивыми, поскольку имеют отрицательное значение энергии связи. С увеличением числа атомов кремния наблюдается незначительный рост удельной энергии связи. Увеличения энергии связи можно добиться, помещая в центр структуры металлические атомы или насыщая поверхностные атомы кремния водородом.
Атом металла, помещенный в центр фуллерена, может проявлять как донорные, так и акцепторные свойства. В зависимости от структуры заполнения электронами атомных орбиталей. Так для меди (Cu) 3-й энергетический уровень заполнен практически полностью, один валентный электрон слабо связан с атомным остовом, вследствие чего медь проявляет донорные свойства. Напротив, для кальция (Ca) возможно проявление акцепторных свойств, в связи с полным заполнением 4s подуровня, очевидно, при малом расстоянии относительно кремния начинает заполняться 4р подуровень; с увеличением расстояния от кремния кальций начинает проявлять донорные свойства. Характерно, что энергия связи для CuSin меньше чем для структур CaSin, это можно объяснить большей разницей электроотрицательностей между кремнием (1.95) и кальцием (1.0) по отношению к кремнию (1.95) и меди (1.7) [25].
Инкапсулирование
исследуемых структур металлическими атомами приводит к повышению ![]() , однако, для структуры
с 36 атомами кремния при добавлении меди данная зависимость нарушается
поскольку в этом случае металл практически не связан с кремниевым остовом. При
гидрировании кремниевого фуллерена вакантные связи насыщаются, что способствует
значительному понижению верхнего заполненного уровня и увеличению разницы
, однако, для структуры
с 36 атомами кремния при добавлении меди данная зависимость нарушается
поскольку в этом случае металл практически не связан с кремниевым остовом. При
гидрировании кремниевого фуллерена вакантные связи насыщаются, что способствует
значительному понижению верхнего заполненного уровня и увеличению разницы ![]() и возрастанию работы
выхода.
и возрастанию работы
выхода.
Таким образом, меняя
структуру фуллерена, можно получать материалы с заведомо необходимыми
свойствами, в частности величину работы выхода, электронного сродства и ширину ![]() щели т.е. аналога запрещенной
зоны объемного материала.
щели т.е. аналога запрещенной
зоны объемного материала.
Литература
1. Пул Ч., Оуэнс Ф. Нанотехнологии. – М.: Техносфера, 2006. – 336 с.
2. Керл Р.Ф. Истоки открытия фуллеренов: эксперимент и гипотеза // Успехи физич. наук. – 1998. – Т. 168. – № 3 – С. 331-342.
3. Huira H., Miyazaki T., Kanayama T. Formation of Metal-Encapsulating Si Cage Clusters // Phys. Rev. Lett. – 2001. – Т. 86. – №9. – P. 1733-1736.
4. Hoffmann M.A., Wrigge
G., Issendorff B.V., Müller J., Ganteför G., Haberland H. Ultraviolet
photoelectron spectroscopy of ![]() to
to ![]() // Eur. Phys. J. D. – 2001. – V.
16. ‑ № 1-3. – P. 9-11.
// Eur. Phys. J. D. – 2001. – V.
16. ‑ № 1-3. – P. 9-11.
5. Beck T.L., Berry R.S. The interplay of structure and dynamics in the melting of small clasters // J. Chem. Phys. – 1998. – V. 88. ‑ № 6. – P. 3910–3922.
6. Sugano S. Microcluster Physics. // Berlin: Springer, 1991. –375 pp.
7. Курганский С.И., Борщ Н.А. Геометрическая структура и спектральные характеристики электронных состояний кремниевых наночастиц // Физика и техн. полупр. – 2004. – Т. 38. – №5. – С. 580–584.
8. Борщ Н.А., Переславцева Н.С., Курганский С.И. Атомная и электронная структура кремниевых и кремний-металлических наночастиц Si20, Si20–, NaSi20 и KSi20 // Физика и техн. полупр. – 2006. – Т. 40. – № 12. – С. 1457–1462.
9. Мелешко В.П., Мороков Ю.Н., Швейгерт В.А. Структура водородосодержащих кремниевых кластеров. Малые кластеры // Журн. структ. хим. – 1999. – Т. 40. – № 1. – С. 13-20.
10. Yoo S., Zeng X.C. Structures and relative stability of medium-sized silicon clusters. IV. Motif-based low-lying clusters Si21 – Si30 // J. Chem. Phys. – 2006. – V. 124. ‑ № 5. – P. 054304.
11. Kumar V. Novel caged clusters of silicon: Fullerenes, Frank–Kasper polyhedron and cubic // Bull. Mater. Sci. ‑ 2003. ‑V. 26. ‑ № 1. ‑ P. 109–114.
12. Pei Y., Gao Yi, Zeng X.C. Exohedral silicon fullerenes: SiNPtN/2 20≤ N ≤ 60 // J. Chem. Phys. – 2007. – V. 127. ‑ №4. – P. 044704.
13. Gao Yi., M4Si28 (M = Al,Ga): Metal-encapsulated tetrahedral silicon fullerene // J. Chem. Phys. – 2005. – V. 123. ‑ № 20. – P. 204325.
14. Park M.-H., Kim M.G., Joo J., Kim K., Kim J., Ahn S., Cui Yi, Cho J. Silicon nanotube battery anodes // Nano Lett. – 2009. – V. 9. – №. 11. – Р. 3844-3847.
15. Мазуренко Е.A., Дорошенко М.Н., Герасимчук А.И. Синтез, свойства и моделирование кремниевых и германиевых нанотрубок // Украинский химический журнал. – 2008. – Т. 74. – № 11. – С. 3-15.
16. Powell D., Silicene: It could be the new graphen // Science News. – 2011. ‑ V. 179. ‑ № 9. – P. 14.
17. Соловьев М.Е., Соловьев М.М. Компьютерная химия. – М.: Солон-Пресс, 2005. – 536 с.
18. Stewart J.J.P. Optimization of parameters for semiempirical methods // J. Comput. Chem. – 1989. – V. 10. – №2. – P. 209-264.
19. Stewart J.J.P. Optimization of Parameters for Semi-Empirical Methods III-Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, Tl, Pb, and Bi // J. Comput. Chem. – 1991. – V. 12. – №3. – P. 320-341.
20. Чернозатонский Л.А. Новый класс диоксидных нанотруб МO2 (М = Si, Ge, Sn, Pb) из "квадратных" решеток атомов – их структура и энергетические характеристики // Письма в ЖЭТФ. – Т. 80. ‑ № 10. – С. 732-736.
21. Курганский С.И., Борщ Н.А. Геометрическая и электронная структура кремниевых и кремниево-металлических наночастиц. // Изв. РАН. Сер. физич. – 2004. – Т. 68. – № 7. – С. 1023-1025.
22. Филиппов В.В., Переславцева Н.С., Курганский С.И. Квантовохимическое моделирование структуры напряженных нанокристаллов кремния на германиевой подложке // Изв. РАН. Сер. физич. – 2008. – Т. 72. ‑ №9. – С. 1314-1316.
23. Филиппов В.В., Власов А.Н. Моделирование электронных свойств кремниевых наночастиц с плотной атомной упаковкой // Известия вузов. Физика. – 2010. – № 1 – С. 70-75.
24. Власов А.Н., Филиппов В.В. Квантово-энергетические и кинетические свойства материалов кремниевой наноэлектроники на основе кластеров Si2-Si10 [Электронный ресурс] // Журнал радиоэлектроники (электронный журнал). – 2011. – № 8. – Режим доступа: http://jre.cplire.ru/jre/aug11/6/text.html.
25. Бацанов С.С. Структурная химия. Факты и зависимости. – М.: Диалог–МГУ, 2000. – 292 с.