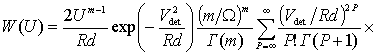УДК 621.391
ОБНАРУЖЕНИЕ РАДИОЛОКАЦИОННОГО СИГНАЛА В УСЛОВИЯХ МНОГОЛУЧЕВОСТИ
А. В. Болдин, Р. П. Быстров, В. Л. Румянцев, А. В. Хомяков
ОАО Центральное конструкторское бюро аппаратостроения, г. Тула
Получена 26 октября 2011 г.
Аннотация. Проведена оценка степени влияния мультипликативной помехи на эффективность обнаружения радиолокационного сигнала, наблюдаемого на границе раздела двух сред, в условиях воздействия аддитивного шума.
Ключевые слова: обнаружение цели, радиолокационный сигнал, отношение правдоподобия, интерференционный множитель.
Abstract. Estimation of the degree of multiplicative interference influence on radar signal detection efficiency has been carried out, the signal being observed in two-environment interface with adaptive noise influence.
Keywords: target detection, radar signal, likelihood ratio, interference coefficient.
Введение
При распространении радиоволн на трассе РЛС–объект отраженный сигнал претерпевает множественные переотражения от подстилающей поверхности, что приводит к изменению его тонкой структуры [1,2]. Действительно, при радиолокации наземных объектов, когда углы скольжения невелики, сигнал на выходе линейной части приемника формируется прямым и переотраженным поверхностью раздела сигналом. Если ограничиться случаем, когда излучение и прием согласованы по поляризации, то амплитуда сигнала, отраженного от объекта с учетом переотражений может быть представлена в виде
где ![]() - множитель ослабления (квадрат
интерференционного множителя) [3].
- множитель ослабления (квадрат
интерференционного множителя) [3].
В соотношении (1) ![]() состоит из суммы
детерминированной
состоит из суммы
детерминированной ![]() и
случайной
и
случайной ![]() компоненты;
компоненты;
![]() сигнал,
отраженный от объекта в свободном пространстве;
сигнал,
отраженный от объекта в свободном пространстве; ![]() -аппаратурная константа, зависящая от потенциала РЛС,
эффективной поверхности рассеяния, дальности до цели и коэффициента передачи
приемного устройства;
-аппаратурная константа, зависящая от потенциала РЛС,
эффективной поверхности рассеяния, дальности до цели и коэффициента передачи
приемного устройства; ![]() -прямой
сигнал, отраженный от разрешаемого участка поверхности. Из (1) видно, что
влияние поверхности раздела на отраженный сигнал сводится к мультипликативному
его искажению по случайному закону изменения величины
-прямой
сигнал, отраженный от разрешаемого участка поверхности. Из (1) видно, что
влияние поверхности раздела на отраженный сигнал сводится к мультипликативному
его искажению по случайному закону изменения величины ![]() . Уместно отметить, что анализ
влияния мультипликативной помехи на характеристики отраженного сигнала был
приведен в ряде работ [2-4]. Однако, особенностью указанных работ является то,
что статистические характеристики сигнала
. Уместно отметить, что анализ
влияния мультипликативной помехи на характеристики отраженного сигнала был
приведен в ряде работ [2-4]. Однако, особенностью указанных работ является то,
что статистические характеристики сигнала ![]() не связаны с физическими параметрами
поверхности раздела. Для установления такой зависимости определим плотность
распределения вероятностей амплитуды сигнала
не связаны с физическими параметрами
поверхности раздела. Для установления такой зависимости определим плотность
распределения вероятностей амплитуды сигнала ![]() и алгоритм обнаружения такого сигнала.
и алгоритм обнаружения такого сигнала.
Характеристики мультипликативного сигнала
Запишем соотношение (1) в виде
![]() , (2)
, (2)
где ![]() . Из (1,2) видно, что для определения
. Из (1,2) видно, что для определения ![]() необходимо вычислить
необходимо вычислить ![]() , что, в свою очередь,
приводит к необходимости обоснованного выбора законов распределения флуктуаций
прямого сигнала и множителя ослабления. В [3,4] показано, что следствием
равенства дисперсий квадратурных составляющих диффузной компоненты поля и нормального
закона распределения высоты неровностей, является распределение множителя ослабления
по закону Райса
, что, в свою очередь,
приводит к необходимости обоснованного выбора законов распределения флуктуаций
прямого сигнала и множителя ослабления. В [3,4] показано, что следствием
равенства дисперсий квадратурных составляющих диффузной компоненты поля и нормального
закона распределения высоты неровностей, является распределение множителя ослабления
по закону Райса
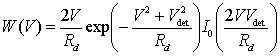 , (3)
, (3)
где ![]() ;
; ![]() - модуль коэффициента отражения [3];
- модуль коэффициента отражения [3]; ![]() - фаза коэффициента отражения;
- фаза коэффициента отражения; ![]() ;
; ![]() -коэффициент Френеля для
заданной поляризации и угла скольжения
-коэффициент Френеля для
заданной поляризации и угла скольжения ![]() ;
; ![]() нетрудно определить из соотношения
нетрудно определить из соотношения ![]() , в котором
, в котором ![]() - среднеквадратическое
значение высоты неровностей;
- среднеквадратическое
значение высоты неровностей;![]() - волновое число;
- волновое число; ![]() -среднеквадратическое значение коэффициента
диффузного рассеяния [2,3].
-среднеквадратическое значение коэффициента
диффузного рассеяния [2,3].
Выбор ![]() в значительной мере произволен.
Очевидно, что плотность распределения вероятностей (ПРВ)
в значительной мере произволен.
Очевидно, что плотность распределения вероятностей (ПРВ) ![]() должна охватывать широкий класс
распределений от островершинных до распределений с плоской вершиной, включая
экспоненциальное, как частный случай, и иметь возможность при некоторых
значениях параметров вырождаться в нормальное распределение. Этим требованиям в
полной мере отвечает квадрат распределения Накагами, описывающий в большинстве
случаев, как это показано в [6], закон распределения флуктуаций сигнала,
отраженного от реальных малоразмерных наземных объектов. То есть
должна охватывать широкий класс
распределений от островершинных до распределений с плоской вершиной, включая
экспоненциальное, как частный случай, и иметь возможность при некоторых
значениях параметров вырождаться в нормальное распределение. Этим требованиям в
полной мере отвечает квадрат распределения Накагами, описывающий в большинстве
случаев, как это показано в [6], закон распределения флуктуаций сигнала,
отраженного от реальных малоразмерных наземных объектов. То есть
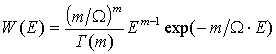 .
(4)
.
(4)
Смысл параметров ![]() достаточно
подробно рассмотрен в [8]. На основе известного преобразования [7]
достаточно
подробно рассмотрен в [8]. На основе известного преобразования [7]
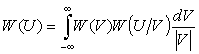
после соответствующих вычислений нетрудно получить
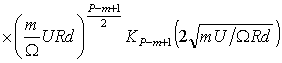 . (5)
. (5)
Здесь ![]() - цилиндрическая функция мнимого
аргумента. Воспользовавшись соотношением (5), определим
- цилиндрическая функция мнимого
аргумента. Воспользовавшись соотношением (5), определим ![]() начальные моменты ПРВ мультипликативного сигнала
начальные моменты ПРВ мультипликативного сигнала
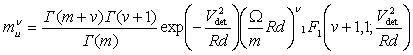 . (6)
. (6)
Здесь ![]() - вырожденная гипергеометрическая
функция. Из (6) нетрудно определить основные физически измеряемые величины:
математическое ожидание, дисперсию, коэффициент вариации. Так, для математического
ожидания, дисперсии мультипликативного сигнала будут справедливы соотношения:
- вырожденная гипергеометрическая
функция. Из (6) нетрудно определить основные физически измеряемые величины:
математическое ожидание, дисперсию, коэффициент вариации. Так, для математического
ожидания, дисперсии мультипликативного сигнала будут справедливы соотношения:
![]() =
=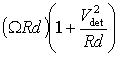 ; (7)
; (7)
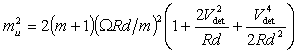 ;
(8)
;
(8)
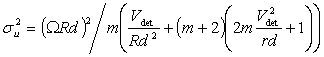 . (9)
. (9)
Коэффициент
вариации сигнала ![]() c учетом (7), (9) запишется в виде
c учетом (7), (9) запишется в виде
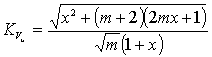 ,
,
где
![]() .
.
Статистические характеристики сигнала, описываемого распределением (5), достаточно подробно рассматриваются в работах авторов [5,6].
Рассмотрим некоторые характерные случаи радиолокационного наблюдения:
1.
Цель находится на шероховатой
поверхности в интерференционных максимумах поля ![]() >> 1,0.
>> 1,0.
2.
Цель находится на шероховатой
поверхности в интерференционных максимумах поля ![]() << 1,0.
<< 1,0.![]()
Определяя величину ![]() как
как ![]() , нетрудно убедиться, что вследствие
многолучевого распространения радиоволн
, нетрудно убедиться, что вследствие
многолучевого распространения радиоволн ![]() может достигать значений
может достигать значений ![]() .
.
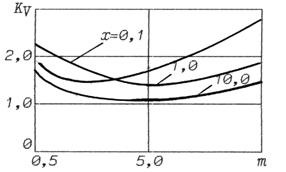
На рис.1, 2 показана зависимость коэффициента вариаций
от параметров ![]() ,
,
![]() . Из рисунков
видно, что в интерференционных минимумах поля
. Из рисунков
видно, что в интерференционных минимумах поля ![]() при любых значениях
при любых значениях ![]() больше единицы, причем его
численное значение пропорционально коэффициенту вариации сигнала, отраженного
от цели в свободном пространстве. В интерференционных максимумах при больших
значениях
больше единицы, причем его
численное значение пропорционально коэффициенту вариации сигнала, отраженного
от цели в свободном пространстве. В интерференционных максимумах при больших
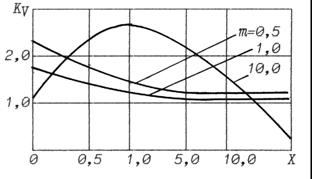
значениях ![]()
![]() <
1,0. Изменение m от 0,5 до 3,0 не приводит к существенному росту
<
1,0. Изменение m от 0,5 до 3,0 не приводит к существенному росту ![]() , асимптотически
приближающемуся к единице при увеличении параметра x.
, асимптотически
приближающемуся к единице при увеличении параметра x.
|
|
|
|
Рис.1. Зависимость коэффициента вариаций от параметра Х при фиксированном m. |
Рис. 2. Зависимость коэффициента вариаций от параметра m при фиксированном Х. |
Таким образом, при многолучевом распространении радиоволн коэффициент вариации отраженного сигнала, как правило, больше единицы и слабо зависит от коэффициента вариации сигнала, отраженного от цели в свободном пространстве. Указанное приводит к росту ошибок обнаружения и распознавания цели устройствами, рассчитанными в соответствии с вероятностными характеристиками отраженного сигнала, без учета множественных переотражений от подстилающей поверхности.
Эффективность обнаружения сигналов, отраженных от объектов, в условиях многолучевости
При проектировании устройств обнаружения объектов, находящихся на границе раздела двух сред, необходимо учитывать изменение характеристик отраженного сигнала вследствие многолучевого распространения радиоволн. Указанное изменение сводится в основном к увеличению глубины флуктуаций и замираниям отраженного сигнала. Для оценки степени влияния мультипликативной помехи на эффективность обнаружения целесообразно синтезировать решающее правило для сигнала, описываемого распределением (5), найти характеристики обнаружения и сравнить их с характеристиками для сигнала, отраженного от объектов в свободном пространстве.
Введем обозначения ![]() ,
, ![]() . Тогда соотношение (5) примет вид
. Тогда соотношение (5) примет вид
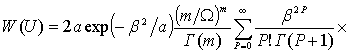
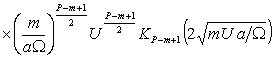 . (10)
. (10)
Положим, что сигнал ![]() после искажения его мультипликативной
помехой подвергается воздействию флуктуирующего аддитивного шума (сигнала,
приходящего от разрешаемой площадки РЛС).
после искажения его мультипликативной
помехой подвергается воздействию флуктуирующего аддитивного шума (сигнала,
приходящего от разрешаемой площадки РЛС).
Для некогерентной схемы обработки в режиме слабого сигнала после квадратичного детектора ПРВ помехи будет описываться экспоненциальным распределением
![]() ,
(11)
,
(11)
где ![]() - мощность помехи, определяемая
характеристиками РЛС и типом подстилающей поверхности. Вычислим
- мощность помехи, определяемая
характеристиками РЛС и типом подстилающей поверхности. Вычислим ![]() , где
, где ![]() . Здесь
. Здесь ![]() – номер элемента выборки
при междупериодной обработке сигнала.
– номер элемента выборки
при междупериодной обработке сигнала.
Воспользовавшись правилом преобразования ПРВ при суммировании независимых случайных величин, после громоздких вычислений, на основе (10), (11), получим
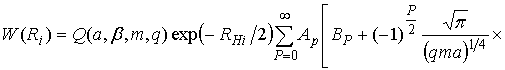
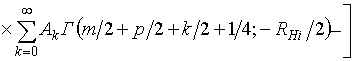 . (12)
. (12)
где ![]()
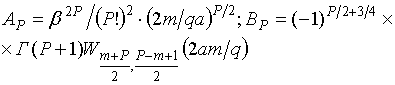 ;
;
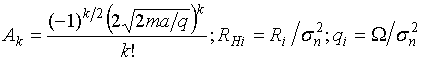 .
.
![]() - функция Уитеккера;
- функция Уитеккера; ![]() - неполная гамма-функция [9].
- неполная гамма-функция [9].
Здесь и в дальнейшем
полагается, что интервал дискретизации процесса ![]() больше интервала его корреляции, подстилающая поверхность в пределах
разрешаемой площадки однородна по геометрическим и электрическим свойствам.
Прием ведется на согласованной поляризации. Тогда в соответствии с (12),
решающее правило обнаружения запишется в виде [10]
больше интервала его корреляции, подстилающая поверхность в пределах
разрешаемой площадки однородна по геометрическим и электрическим свойствам.
Прием ведется на согласованной поляризации. Тогда в соответствии с (12),
решающее правило обнаружения запишется в виде [10]
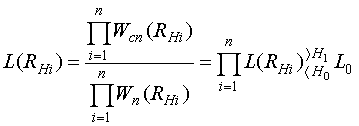 . (13)
. (13)
В соотношении (13) ![]() - пороговое значение, определяемое
выбранным критерием обнаружения. Прологарифмировав (13), получим
- пороговое значение, определяемое
выбранным критерием обнаружения. Прологарифмировав (13), получим
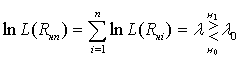 , (14)
, (14)
где ![]() .
.
Если в (14) ограничиться конечным числом членов, то
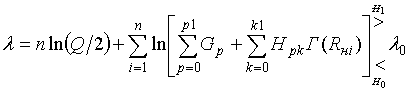 . (15)
. (15)
Здесь ![]()
![]()
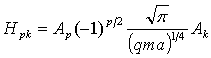 .
.
Число членов ряда ![]() и
и ![]() выбирается исходя из приемлемой
точности вычисления отношения правдоподобия. Устройство обнаружения включает в
свой состав схемы весового суммирования, блоки вычисления весовых множителей,
необходимые для расчета полиномов, блоки вычисления гамма-функции, блоки
логарифмирования, а также пороговое устройство.
выбирается исходя из приемлемой
точности вычисления отношения правдоподобия. Устройство обнаружения включает в
свой состав схемы весового суммирования, блоки вычисления весовых множителей,
необходимые для расчета полиномов, блоки вычисления гамма-функции, блоки
логарифмирования, а также пороговое устройство.
Оценка эффективности синтезированного устройства обнаружения проводилась на основе метода статистического моделирования.
Выборка случайных величин ![]() обрабатывалась в
соответствии с решающим правилом (15). Результаты обработки в виде кривых
обнаружения представлены на рис.3. Вычисления проводились при
обрабатывалась в
соответствии с решающим правилом (15). Результаты обработки в виде кривых
обнаружения представлены на рис.3. Вычисления проводились при ![]() = 50,0
(интерференционный максимум
= 50,0
(интерференционный максимум ![]() >>1,0);
>>1,0); ![]() =1,0;
=1,0; ![]() = 0,1 (интерференционный минимум) и различных
значениях
= 0,1 (интерференционный минимум) и различных
значениях ![]() .
.
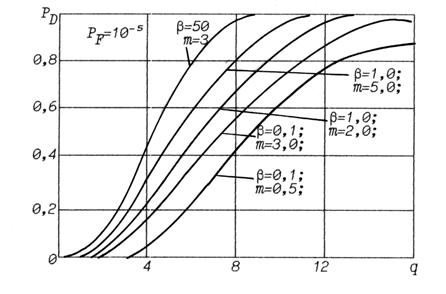
Рис. 3. Зависимость вероятности обнаружения от
отношения сигнал/шум при различных значениях ![]() и
и ![]() .
.
Из рис. 3 видно, что в
интерференционных максимумах качество обнаружения существенно выше, чем в
интерференционных минимумах и практически не зависит от значения параметра ![]() . При
. При ![]() =1,0 решающее влияние на
качество обнаружения оказывает значение параметра
=1,0 решающее влияние на
качество обнаружения оказывает значение параметра ![]() , определяющее глубину флуктуации полезного
сигнала. Наиболее значительно вероятность обнаружения падает при
, определяющее глубину флуктуации полезного
сигнала. Наиболее значительно вероятность обнаружения падает при ![]() < 1,0 и
< 1,0 и ![]() < 1,0 , т.е. когда
цель наблюдается в интерференционном минимуме и
< 1,0 , т.е. когда
цель наблюдается в интерференционном минимуме и ![]() ее в свободном пространстве больше единицы.
ее в свободном пространстве больше единицы.
Таким образом, на характеристики обнаружения целей, находящихся у раздела двух сред, оказывает существенное влияние не только глубина флуктуаций сигнала, отраженного объектом в свободном пространстве, но и свойства подстилающей поверхности. Вследствие этого, при проектировании устройств обнаружения малоразмерных объектов на фоне подстилающей поверхности целесообразно использовать методы, уменьшающие влияние мультипликативной помехи на эффективность РЛС.
Результаты могут быть полезны специалистам, научным сотрудникам в области радиотехники при оценке эффективности устройств обнаружения случайных сигналов.
Литература
1. Акиншин Н.С., Быстров Р.П., Румянцев В.Л., Соколов А.В. Миллиметровая радиолокация: методы обнаружения негауссовских сигналов. Под ред.Р.П. Быстрова. //М: Радиотехника, 2010. - 528 с.
2. Островитянов Р.В., Басалов Ф.А. Статистическая теория радиолокации протяженных целей. //М.: Радио и связь, 1982. - 232 с.
3. Beckman P., Spizzichino A. The scattering of еlectromagnetic waves from rough surfaces. Oxford. Pergamon Press. 1963.
4. Кулемин Г.П., Разсказовский В.Б. Рассеяние миллиметровых волн поверхностью Земли под малыми углами. //Киев: Наук. Думка, 1987. - 232 с.
5. Румянцев В.Л., Николаев В.А., Илюха С.А. Характеристики выбросов мультипликативного сигнала при многолучевом распространении радиоволн. // Электроника и техника СВЧ и КВЧ, 1994. №1. - с.19-25.
6. Акиншин Н.С., Румянцев В.Л., Процюк С.В. Поляризационная селекция и распознавание радиолокационных сигналов. //Тула: Лидар, 2000. - 316 с.
7. Крамер Г. Математические методы статистики. Пер. с англ. под ред. А.Н. Колмогорова. // М.: Мир, 1975. 648 с.
8. Тихонов В.И. Статистическая радиотехника. //М.: Радио и связь, 1982. -623 с.
9. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. //М.: ГИФМЛ, 1962. - 1097 с.
10. Репин В.Г., Тартаковский Т.П. Статистический синтез при априорной неопределенности и адаптация информационных систем. //М.: Сов. радио, 1977. - 432 с.