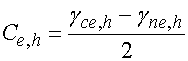УДК 621.396.67

ДВУХПОЛЯРИЗАЦИОННОЕ ДВУХСЛОЙНОЕ ПЛАНАРНОЕ ЗЕРКАЛО

С. Е. Банков
ИРЭ им. В.А. Котельникова РАН

Получена 12 ноября 2012 г.

Аннотация. Рассмотрены вопросы моделирования и проектирования важного элемента планарной СВЧ оптики – двухслойного двухполяризационного зеркала на основе плоских волноводов. Предложена конструкция планарного зеркала, обеспечивающая передачу с одного слоя структуры на другой с одновременным отражением назад волн двух ортогональных поляризаций. Конструкция зеркала содержит два плоских волновода, связанных через общий экран в виде частопериодической ленточной решетки. В работе анализируются собственные волны таких плоских волноводов. Показана, что выбором параметров структуры можно обеспечить одинаковые значения линейных коэффициентов связи для волн ортогональных поляризаций. Предложена упрощенная модель зеркала, основанная на предположении о малом возмущении волн несвязанных волноводов на участке связи. Представлена численная оценка параметров зеркала, полученная в рамках приближенной модели.

Ключевые слова: планарное зеркало, двухслойное планарное зеркало, двухполризационное планарное зеркало, плоский волновод.

Abstract. Problems of modeling and design of an important element of microwave planar optics – dual layer dual polarized mirror on the base of parallel plate waveguides are considered. Construction of the planar mirror that provides energy transmission for waves of two orthogonal polarizations from one layer to another with simultaneous wave reflection in the backward direction is proposed. The mirror contains two parallel plate waveguides coupled through a common screen in form of array of metal strips. Eigen modes of such coupled waveguides are analyzed. It is shown that a correct choice of the structure parameters provides the same values of coupling coefficients of waves with orthogonal polarizations. An approximate model of the mirror obtained under the assumption about weak perturbation of parallel plate waveguide modes in the coupling region is obtained. Parameters of the planar mirror are numerically calculated with help of the model.

Keywords: planar mirror, dual layer planar mirror, dual polarized planar mirror, parallel plate waveguide.

Постановка задачи

В последнее время в развитии техники миллиметрового и субмиллиметрового диапазонов (ММД и СММД) наблюдается устойчивая тенденция перехода от волноводных принципов формирования и пространственной обработки полей к оптическим принципам. Такая тенденция является продолжением наблюдавшейся ранее тенденции перехода от «проводного» механизма передачи электромагнитной энергии, связанного с использованием линий передачи с Т и квази – Т – волнами к волноводному механизму, связанному с использованием диэлектрических, металлических, щелевых, полосковых и т.д. волноводов [1]. Поскольку концентрация поля в волноводе существенно ниже, чем в линии передачи, то и затухание волн, в особенности обусловленное потерями в металлических элементах конструкции в волноводах значительно меньше, чем в линиях передачи. Развивая эту идею дальше, можно отказаться от направляющих структур полностью и перейти к обработке и передаче волновых пучков, поле которых распределено в еще большей области пространства, чем даже в случае волновода. Основными элементами таких оптических или точнее квазиоптических устройств служат различные зеркала и линзы.

Указанная тенденция затронула не только объемные устройства, но и интегральные схемы, которые также могут строиться с использованием оптических принципов. В последние десятилетия был предложен ряд конструкций, линз [2], зеркал [3], резонаторов [4], фильтров [5], в основу которых положено преобразование двумерных волновых пучков, распространяющихся в, так называемых, планарных волноводах (ПЛВ). Чаще всего в качестве ПЛВ используются плоские волноводы (ПВ) в виде двух параллельных металлических экранов, пространство между которыми заполнено диэлектриком или планарные диэлектрические волноводы (ПЛДВ), представляющие собой диэлектрическую пластину с поверхностными волнами.

Устройства указного типа активно исследуются сейчас в связи с повышением актуальности технического освоения коротковолновой части ММД и СММД. Таким образом, можно говорить о появлении нового направления в данной области науки и техники, которое можно назвать планарной или интегральной СВЧ оптикой. Отметим, что наиболее вероятной областью практического использования обсуждаемых устройств является проектирование различных антенн ММД и СММД.

Как отмечалось выше, одним из базовых элементов планарной СВЧ оптики является планарное зеркало. В работе [3] используются для построения двухзеркальной печатной антенны зеркала на основе ПВ. Роль отражающей поверхности в них играют решетки из металлических цилиндров. Развитием идеи планарного зеркала служат двухслойные планарные зеркала, которые анализируются в работах [6], [7]. Достоинством двухслойного зеркала является то, что в нем отражении волн сопровождается ее переходом с одного слоя на другой. В результате падающие и отраженные волны оказываются пространственно разнесенными и не влияют друг на друга. Таким образом, преодолевается один из существенных недостатков традиционных зеркальных систем, связанный с затенением одних элементов другими.

Вместе с тем планарные зеркала, построенные на основе ПВ, имеют по сравнению с традиционными объемными зеркалами такой существенный недостаток как поляризационная избирательность. Точнее, при использовании одноволновых ПВ они являются однополяризационными устройствами. Вместе с тем, многие современные радиоэлектронные системы используют волны двух ортогональных поляризаций. Поэтому актуальной задачей развития планарной СВЧ оптики является создание двухполяризационных, двухслойных зеркал, сочетающих отсутствие затенения с возможностью работы на волнах двух ортогональных поляризаций.

В данной работе анализируется один из возможных вариантов построения указанных планарных зеркал. В первой части работы рассматривается простейшее решение, связанное с использованием многомодовых ПВ и участком связи в виде щели в общем экране ПВ. Это решение развивает планарное зеркало, предложенное в работе [6].

В первом разделе данной работы анализируются недостатки указанного технического решения и предлагается модифицированная конструкция зеркала, содержащая участок связи ПВ в виде частопериодической ленточной решетки (ЧПР). Во втором разделе анализируются собственные волны связанных через ЧПР ПВ. Там же будет показано, что в такой структуре возможна реализация режима, при котором волны обеих поляризаций имеют близкие линейные коэффициенты связи (ЛКС). В третьем разделе в рамках приближенной модели, основанной на предположении о слабом возмущении волн ПВ на участке связи анализируются характеристики зеркала с прямолинейной границей.

1. Двухслойное зеркало на многомодовых ПВ и участком связи в виде щели в экране ПВ

В этом разделе в качестве отправной точки для последующего исследования мы рассмотрим простейшую модификацию двухслойного планарного зеркала, исследованного в работе [6].

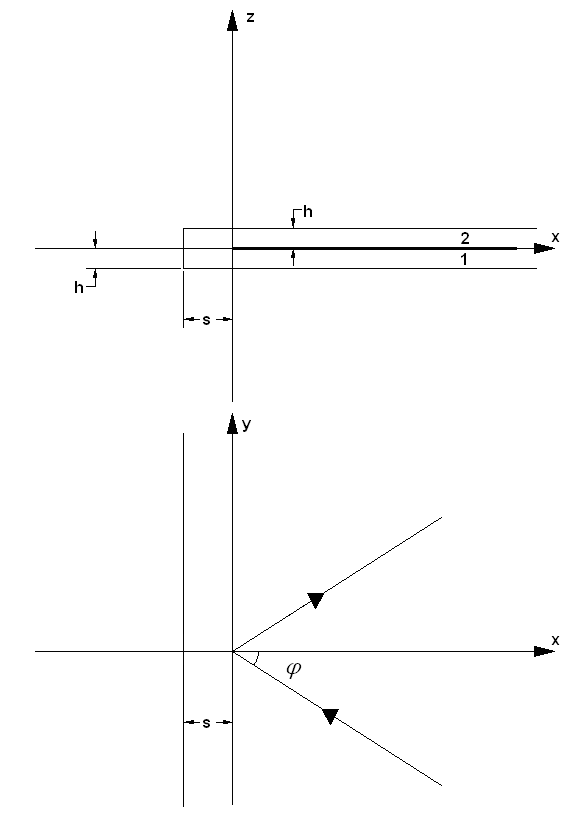
В работе [6] рассмотрена структура, показанная на рис. 1 в предположении о том, что ПВ высотой , расположенные в области являются одноволновыми ПВ, в которых может распространяться только основная Т – волна, вектор электрического поля которой параллелен оси 0z. Поэтому, такое устройство может работать только на волнах вертикальной поляризации, если следовать рис. 1.

Рис. 1. Планарное зеркало с щелевой областью связи

Для того, чтобы в ПВ распространялась дополнительно одна волна горизонтальной поляризации типа его высота должна удовлетворять неравенству [8]:

, (1)

где - длина волны в среде, заполняющей ПВ.

Отметим, что при выполнении неравенства (1) в ПВ высотой распространяется также еще одна волна вертикальной поляризации типа , постоянная распространения которой равна постоянной распространения - волны.

Таким образом, мы видим, что для решения поставленной задачи о создании двухполяризационного зеркала необходимо использовать многоволновые ПВ. Данное обстоятельство является важным фактором, который, как будет показано ниже, существенно влияет на структуры параметры устройства.

Область связи двух ПВ, как видно из рис. 1, представляет щель в общем экране ПВ при , ориентированную вдоль оси 0у. В области щели шириной мы имеем также ПВ, но удвоенной высоты . В общем случае, как показано в работе [6], зеркало, выполненное даже на одноволновых ПВ может работать в двух разных режимах: квазистатическом и динамическом. В первом режиме в области может распространяться только основная волна ПВ высотой , а во втором в этой области могут распространяться две волны.

В квазистатическом режиме передача энергии из ПВ1 в ПВ2 достигается за счет разной фазы коэффициентов отражения четной и нечетной относительно плоскости волн от обрыва металлизации при и от вертикальной стенки при . В динамическом режиме механизм передачи энергии из одного ПВ в другой меняется. Она осуществляется за счет разности постоянных распространения четных и нечетных волн ПВ в области . Таким образом, область связи функционирует аналогично волноводному щелевому направленному ответвителю [9].

Можно предположить, что при еще большем увеличении высоты ПВ, задаваемом условием (1) планарное зеркало тем более будет работать в динамическом режиме на эффекте биения собственных вол ПВ. В связи с этим введем параметры, характеризующие интенсивность эффекта распределенной связи. Традиционно в этом качестве используется линейный коэффициент связи (ЛКС), который определяется следующим образом:

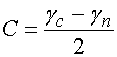, (2)

где - постоянные распространения четной и нечетной волн на участке связи. Под четными волнами мы понимаем волны, поле которых в плоскости симметрии удовлетворяет граничному условию на магнитной стенке. Поле нечетных волн удовлетворяет условиям на электрической стенке. В ПВ высотой при выполнении условия (1) будут распространяться при любом следующие волны:

четные Е – волны: , (3)

четные Н – волны: ,

нечетные Е – волны: ,

нечетные Н – волны: .

При значениях больших могут дополнительно распространяться также волны типов . Постоянные распространения волн равны , где - волновое число среды, заполняющей ПВ, - номер волны.

Из соотношений (3) видно, что четные и нечетные волны разной поляризации определяются однозначно во всех случаях кроме нечетных Е – волн, среди которых имеются две волны . Нас интересует основная Т – волна.

Отметим, что все волны на участке связи распространяются независимо в силу ортогональности собственных волн ПВ. Их связь возникает в плоскости на нерегулярности в виде обрыва экранов ПВ.

Можно отметить следующие свойства рассматриваемой структуры. Она обладает симметрией относительно плоскости . Поэтому к ней можно применить метод симметрии [9] и рассматривать два случая четного и нечетного возбуждения. При таком подходе четные и нечетные волны не связываются друг с другом даже на указанной нерегулярности. Волны Е и Н – типов не связываются при нормальном падении волн ПВ, когда , так как структура в этом случае становится двумерной (), а в двумерной структуре волны разных поляризаций не связываются. Поэтому, по крайней мере, для умеренных углов падения связь волн разной поляризации является малым эффектом, которым мы можем пренебречь. Отметим также, что в средне- и длиннофокусных зеркальных системах углы падения на них лучей не превышают 15⁰. Это является дополнительным основанием для сделанного выше приближения.

Таким образом, единственным существенным для нас видом связи волн на обрыве экрана является связь Т и Е₂ – волн. Однако эта связь полностью отсутствует в идеализированной структуре с бесконечно тонкими экранами и пренебрежимо мала для наиболее характерных для планарных зеркал экранов с конечной, но малой толщиной. Поясним данное утверждение. При нечетном возбуждении Е – волнами ПВ при в плоскости симметрии располагается электрическая стенка. Таким образом, в случае экранов нулевой толщины граничные условия в плоскости симметрии для поля при не отличаются от условий при . Поэтому волны проходят нерегулярность без возмущения и взаимной связи. Следовательно, если в ПВ при в качестве возбуждающей волны взяты Т – волны, то они преобразуются в Т – волну ПВ при без связи с Е₂ – волнами.

Таким образом, можно ввести следующие обозначения:

, (4)

где - ЛКС для волн разных поляризаций.

На рис. 2 показана частотная зависимость ЛКС (4). Кривые 1 и 2 соответствуют нормированным на волновое число свободного пространства ЛКС и . Они получены для мм, и ПВ с воздушным заполнением.

Видно, что ЛКС для волн разных поляризаций в несколько раз отличаются друг от друга. Такое отличие практически делает невозможной одновременную передачу мощности из одного ПВ в другой для Е и Н – волн. Отметим, что в приближении слабого возмущения волн ПВ на обрыве экрана, которое, вообще говоря, для рассматриваемой структуры неверно, коэффициенты передачи из одного ПВ в другой полностью определяются ЛКС [6]:

. (5)

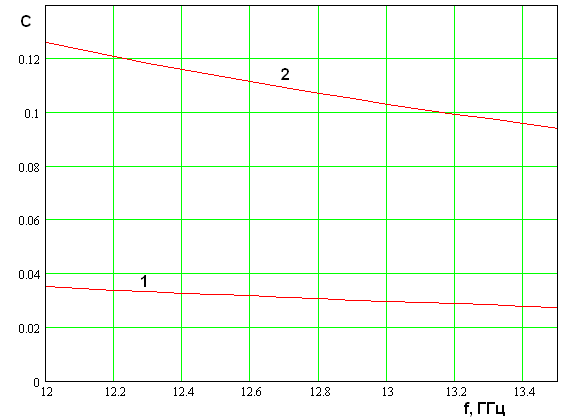
Рис. 2. Частотная зависимость ЛКС

Соотношения (5) будут использованы нами ниже при анализе модифицированных структур, для которых допущение о слабом возмущении волн ПВ на участке связи оправданно.

2. Планарное зеркало с анизотропной ленточной решеткой на участке связи

Представленные выше результаты говорят о том, что простая структура с щелевой областью связи должна быть модифицирована таким образом, чтобы ЛКС для Е и Н – волн были выровнены. Одним из способов решения этой задачи является размещение на участке связи анизотропной ленточной решетки с малым периодом. Такие решетки также называют частопериодическими решетками (ЧПР) [10].

Модифицированная структура показана на рис. 3.

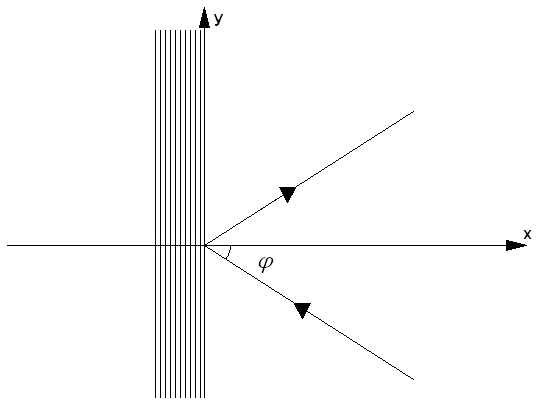
Рис. 3. Планарное зеркало с ЧПР в области связи

Принцип функционирования такого зеркала состоит в следующем. При умеренных углах падения ЧПР оказывает влияние только на Н – волны, имеющие компоненту поля. Волны Е типа, у которых при эта компонента равна нулю практически не «замечают» появления ЧПР. Отметим, что присутствие решетки сказывается только на четной Н – волне, поскольку нечетная волна имеет нулевую компоненту в силу граничных условий на электрической стенке.

Появление решетки, которая для Н – волн может быть описана как пленка с индуктивным импедансом [10], приводит к уменьшению постоянной распространения четной Н – волны и, следовательно, к уменьшению ЛКС , что приведет к сближению ЛКС для волн Е и Н – типов.

В данном разделе мы исследуем собственные волны ПВ высотой , в плоскости симметрии которого расположена ЧПР. На основании этого исследования будут получены ЛКС .

Для описания ЧПР используем эквивалентные граничные условия (ЭГУ) из работы [10]:

, (6)

, ,

, , ,

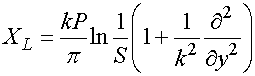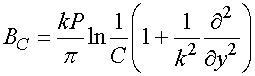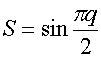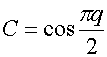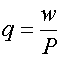где - период решетки, - ширина лент. Дифференциальный оператор из соотношений (5) применяется к величине перед которой он стоит. В ЭГУ (6) входят поля при . Индексы 1,2 соответствуют номерам ПВ (см. рис. 1).

Ищем решение граничной задачи в виде волны, бегущей в плоскости XOY:

, (7)

где волновое число вдоль оси 0у считаем заданной величиной, а волновое число вдоль оси 0х ищем из решения граничной задачи. При анализе планарного зеркала постоянная определяется с углом падения волны (см. формулы (4)).

Решение граничной задачи проводим стандартным образом [11], записывая поля в областях 1 и 2 в виде, удовлетворяющем уравнениям Максвелла и подставляем их в ЭГУ (6). Опуская промежуточные выкладки, приведем окончательный вид дисперсионного уравнения, из которого находится постоянная , а также производные от нее величины:

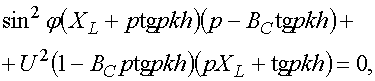(8)

, .

Нас интересует решение уравнения (8) относительно коэффициента замедления . В формуле (8) дифференциальный оператор, входящий в определение параметров ЧПР (6) заменяется множителем .

На рис. 4 показана частотная зависимость ЛКС Е и Н – волн. Кривая 1 соответствует нормированному ЛКС Е – волн, а кривая 2 ЛКС Н – волн. Кривые получены для следующих параметров: мм, мм, , . Видно, что в отличие от кривых на рис. 2 кривые на рис. 4 пересекаются и близки друг к другу в некотором диапазоне частот. Близость ЛКС подтверждает приведенные выше предположения о характере влияния ЧПР на собственные волны ПВ.

Также следует отметить, что по абсолютной величине ЛКС достаточно малы. Данный факт означает, что постоянные распространения Е и Н – волн в области связи незначительно отличаются от постоянных распространения волн изолированных ПВ. С практической точки зрения малые значения ЛКС не являются однозначно положительным фактором, поскольку длина участка связи, необходимая для полной передачи энергии, обратно пропорциональна величине ЛКС. С другой стороны, слабое возмущение волн на границе участка связи означает, что искажения в работе зеркала, обусловленные дифракцией волн на обрыве экрана ПВ, будут сведены к минимуму.

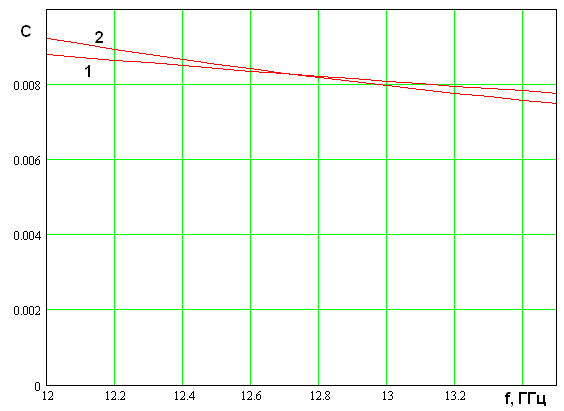
Рис. 4. Частотная зависимость ЛКС планарного зеркала с анизотропной ЧПР

Отсутствие возмущения волн ПВ на границе участка связи позволяет воспользоваться формулами (5), а также соотношениями для коэффициентов отражения , которые получаются при тех же предположениях, что и выражения (5):

. (9)

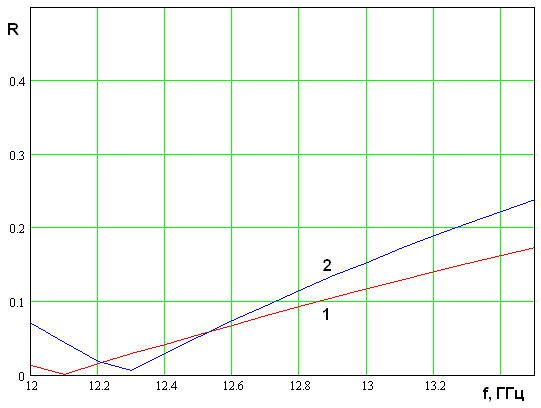
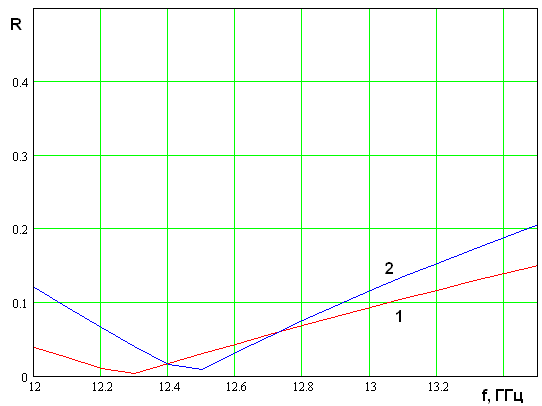
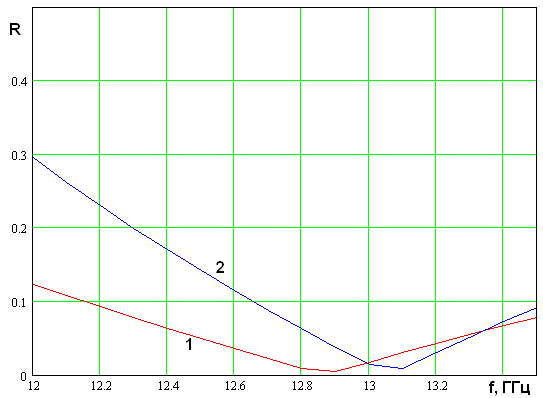
На рис. 5 а-в представлена зависимость модуля коэффициента отражения планарного зеркала. Кривые 1 и 2 соответствуют коэффициентам . Они получены для параметров, приведенных выше, и длине участка связи мм. Кривые на рис. 5 а-в соответствуют углам падения .

Видно, что с увеличением угла падения точка идеального согласования смещается в область высоких частот, а коэффициент отражения на нижней границе диапазона растет.

Рис. 5. Частотная зависимость коэффициента отражения

Таким образом, планарное зеркало данного типа имеет не только ограниченный рабочий диапазон частот, но и ограниченный рабочий диапазон углов падения. Следует отметить, что необходимый диапазон углов падения зависит от типа зеркала и его параметров. Возьмем в качестве примера параболическое зеркало [11]. У него максимальный угол падения луча при освещении зеркала точечным источником, расположенным в фокусе, зависит от отношения размера зеркала к фокусному расстоянию . Например, у весьма короткофокусного зеркала с параметром максимальный угол падения равен . У среднефокусных зеркал с наибольший угол падения не превышает 15⁰. Таким образом, если зеркало сохраняет свою работоспособность в диапазоне углов падения до 20⁰, то оно вполне пригодно для создания длинно- и среднефокусных рефлекторов.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 12-08-12003/12 офи_м.

Литература

1. Банков С.Е. Щелевые интегральные схемы миллиметрового диапазона // Радиотехника и электроника. 2006, Т. 51, №9, с. 1066-1086.

2. Bankov S.E., Bugrova T.I., Levchenko I.V. Planar Lens for Millimeter Wave Integrated Antennas // 24-th European Microwave Conf. Proc., 1994, Nice, France, pp. 76-80.

3. M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, Vol.6, pp. 537-539, Dec. 2007.

4. А.с. 1316063 (СССР). Планарный резонатор / Банков С.Е., Взятышев В.Ф., Широкова О.А. Приор. От 18.11.85. Опубл. БИ №21, 7.06.87.

5. Взятышев В.Ф., Нарытник Т.Н., Рябов Б.А., Емельяненков Б.Н., Банков С.Е. Диэлектрические интегральные схемы КВЧ. Часть 2. Элементы и устройства // Обзоры по электронной технике. - М.: ЦНИИ “Электроника”, 1985, Вып. 13, 73 с.

6. С.Е. Банков. Проектирование и экспериментальное исследование решетки щелевых излучателей. // РЭ, 2004, т.49, №6, с. 701-706.

7. Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.

8. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.

9. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. Шк. 1998.

10. Банков С.Е., Левченко И.В. Эквивалентные граничные условия для ленточной частопериодической решетки на границе раздела двух сред // РЭ, т. ХХХIII, №10, 1988, с. 2045-2050.

11. Корнблит С. СВЧ оптика. М.: «Связь». 1980.