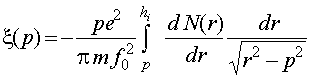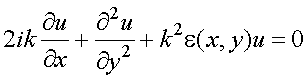УДК 535.37:523.42
РЕШЕНИЕ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ ДИФРАКЦИИ ПРИ РАДИОПРОСВЕЧИВАНИИ ИОНОСФЕРНЫХ СЛОЕВ
Я. А. Илюшин 1, А. Л. Гаврик 2, Ю. А. Гаврик 2, М. И. Бондаренко 2, Т. Ф. Копнина 2, А. А. Смыслов 2
1 МГУ им. М.В. Ломоносова
2 ФИРЭ им. В.А. Котельникова РАН
Статья получена 7 ноября 2013 г.
Аннотация. На основе прямого моделирования поля радиоволн, зондирующих ионосферу, методом численного решения параболического уравнения дифракции исследованы вариации мощности и частоты сигнала, регистрируемого спутником Венеры вдоль траектории движения. Проанализированы условия появления дифракционных искажений поля и возможность применения геометрической оптики при интерпретации данных зондирования тонких периодических слоев плазмы в ионосфере. Выполнена валидация метода обработки данных радиозатмений спутников ВЕНЕРА-15,-16 и показана достоверность многослойных структур на профилях электронной концентрации в нижней ионосфере Венеры.
Ключевые слова: распространение радиоволн, радиозондирование ионосферы.
Abstract. Direct modelling of the electromagnetic field in an occultation experiment, obtained from a numeric solution of the parabolic diffraction equation, was used to investigate power and frequency variations of the signal received by a satellite as it moves on orbit around Venus. Conditions under which diffraction distortions affected the field as well as applicability of geometric optics for the interpretation of layered structure in lower ionosphere visible in actual data was analyzed. Processing method used for Venus-15 and -16 occultation data was validated and existence of multilayer structures on electronic concentration profiles in lower ionosphere was confirmed.
Keywords: radio wave propagation, occultation of ionosphere.
Введение
Несколько десятилетий радиозатменное зондирование развивается в качестве технологии диагностики газовых оболочек космических объектов: Земли [1-5], планет [6-12], комет [13,14] и Солнца [15,16]. Первое зондирование газовой оболочки планеты осуществил в 1965 г. космический аппарат (КА) MARINER-4 [6], пролетевший вблизи Марса. Радиозатменные исследования ионосферы и атмосферы Венеры начались в 1967 г. [7]. Благодаря удачным миссиям КА MARINER-5,-10, ВЕНЕРА-9,-10, PIONEER-VENUS, ВЕНЕРА-15,-16, MAGELLAN, VENUS-EXPRESS проведено ~1000 радиопросвечиваний атмосферы Венеры [6-12]. Накопленный к настоящему времени объем данных радиопросвечивания ионосферы Венеры сравнительно невелик (~900 сеансов), в то время как количество радиопросвечиваний Марсианской ионосферы превышает 6000, а для исследования околоземной оболочки проводятся тысячи радиопросвечиваний в сутки, и общее количество сеансов превысило 2 млн. Совершенствование методики анализа результатов радиопросвечиваний является актуальной задачей, т.к. предоставляет возможность извлечения новой информации об ионосфере [17-19] из многочисленных экспериментальных данных завершенных миссий.
Для исследования тонкой структуры ионосферы целесообразно применять радиоволны дециметрового диапазона, вариации параметров которых при распространении в плазменной оболочке планеты существенно превышают инструментальные флуктуации фазы и мощности сигнала, связанные с ограниченной стабильностью бортовой аппаратуры. Но влияние плазмы на трансформацию низкочастотной радиоволны может привести к нарушению условий лучевых приближений [20,21], на которых основана интерпретация результатов радиозатмений. Например, по данным спутников ВЕНЕРА-15,-16 [22,23] изучены условия фокусировки радиоволн и показано, что вариации параметров сигналов с длиной волны более 50 см могут быть обусловлены не только рефракцией, но и дифракцией радиоволн на границах слоев дневной ионосферы Венеры.
В настоящей работе проводится прямое моделирование поля радиоволны, трансформированного ионосферой планеты. Используется метод численного решения параболического уравнения дифракции, что позволяет анализировать взаимосвязь вариаций мощности и частоты радиосигнала в процессе радиопросвечивания ионосферы Венеры. Целью работы является сопоставление результатов лучевых и дифракционных расчетов с экспериментальными данными КА ВЕНЕРА-15,-16, выявление критерия для оценки правомерности использования геометрической оптики при анализе данных радиопросвечивания многослойных плазменных структур в нижней ионосфере Венеры и валидация лучевой реконструкции вертикальных профилей электронной концентрации по данным радиопросвечивания.
1. Методика моделирования радиопросвечивания ионосферы планеты
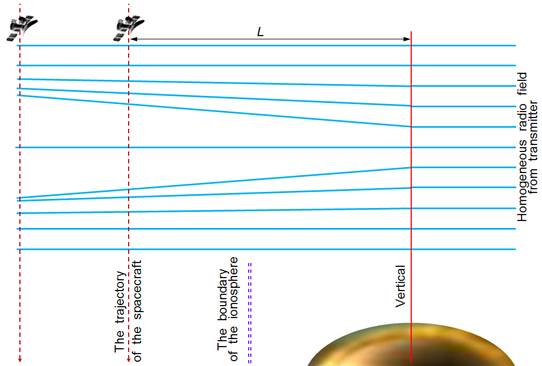
Рассмотрим радиозатменный эксперимент, в котором наземная антенна излучает высокочастотный (f0 > 900 МГц) монохроматический сигнал высокой мощности в направлении Венеры (рис. 1). Расстояние до Венеры превышает 50 млн. км и можно считать, что область диаметром более 105 км вблизи планеты облучается однородной плоской монохроматической высокочастотной радиоволной. Приемник, размещенный на борту КА, перемещается за пределами ионосферы Венеры на расстоянии L от зондируемой области перпендикулярно направлению излучения передатчика и регистрирует вариации параметров радиополя, обусловленные влиянием ионосферы. Расстояние "передатчик–приемник" постоянное (доплеровское изменение частоты отсутствует), параметры регистрируемого поля зависят от L и электронной концентрации на пути распространения радиоволны.
В приближении геометрической оптики изменение направления излучения не изменяет соотношения, применяемые для интерпретации данных радиозатмений, поэтому пределы применимости геометрической оптики в реальных экспериментах, в которых когерентные радиоволны (длины волн λ=32 и 8 см) излучались бортовым передатчиком КА ВЕНЕРА-15,-16 и принимались наземным комплексом, сопоставимы с результатами расчетов в представленной модели. Следовательно, появление эффектов многолучевого распространения и дифракции радиоволн при моделировании позволит выявить условия применимости геометрической оптики в конкретных экспериментах радиопросвечивания.
Рис. 1. Схема эксперимента радиопросвечивания
Приемник, движущийся со скоростью V=6 км/с (рис. 1), регистрирует колебания радиополя u0(t), первоначально заданные вещественной функцией re[u0(t)]. Колебания u0(t) можно представить в комплексной форме, используя понятие аналитического сигнала, при этом амплитуда поля вводится как |u0(t)|, а фаза как arg[u0(t)]. В реальном эксперименте, в отличие от модельных расчетов, при обработке колебаний u0(t) из фазы гетеродинированием исключается компонента ω0t, где t – время, ω0 – частота излучаемой монохроматической радиоволны (в ω0 вводится также поправка на доплеровское смещение из-за взаимного движения передатчика и приемника), амплитуда колебаний нормируется на уровень шума приемника. На выходе приемника формируются квадратурные компоненты сигнала u(t)=A(t)exp{iφ(t)}, где A(t)=|u(t)| и φ(t)=arg[u(t)] это усредненные на интервале времени τ медленные вариации амплитуды и фазы радиополя, обусловленные изменением свойств среды на трассе распространения радиоволны. Далее, и в эксперименте и в модели по квадратурным компонентам u(t) определяются искомые функции мощности P(t)=|u(t)|2 и фазы φ(t)=arg[u(t)] зондирующей радиоволны.
В рассматриваемой модели не учитываются поглощение и рассеяние радиоволн, поэтому девиация мощности P(t), регистрируемая в процессе перемещения КА и усредненная на коротком интервале времени τ, обусловлена деформацией лучевых трубок при рефракции. Рефракционное изменение мощности X(t)=P(t)/P0 нормируется к уровню мощности P0, которая регистрировалась в отсутствии исследуемой ионосферы. Фаза зарегистрированного сигнала φ(t) также изменяется при перемещении приемника на расстояние Vτ, что обусловлено деформацией поверхности волнового фронта радиополя из-за пространственных вариаций показателя преломления околопланетной среды n(h), сквозь которую распространяются радиоволны (h – высота над поверхностью планеты). Приращение фазы за время τ однозначно определяется по квадратурным компонентам сигнала u(t), если приращение фазы меньше π. Для нахождения монотонной функции φ(t) эти приращения суммируются, что может приводить к накоплению погрешности при случайных сбоях аппаратуры и затрудняет анализ мелкомасштабных флуктуаций при наличии монотонного изменения фазы. Поэтому удобнее не суммировать приращения фазы, а анализировать частоту сигнала f(t)={arg[u(t-τ)]–arg[u(t+τ)]}/4πτ, определяемую по приращению фазы. Именно мгновенная частота сигнала f(t)=(2π)-1∙dφ(t)/dt связана интегральным соотношением с высотным профилем электронной концентрации N(h) при решении обратной задачи радиопросвечивания [19], а мелкомасштабные флуктуации f(t) являются характеристикой уровня инструментального шума.
При зондировании сферически-симметричной ионосферы изменение частоты f(t) и рефракционное изменение мощности X(t) регистрируемого сигнала связаны с углом рефракции x(t) в лучевом приближении и отсутствии поглощения радиоволн следующими известными соотношениями [19]:
p(t) = R0 + hr(t) + L · x(t), (2)
X(t) = 1 + [L∙V–1] ∙ dx(t)/dt. (4)
Xf(t) = 1 + [λ∙L∙V–2] ∙ df(t)/dt. (5)
где R0 – радиус планеты; f0 и λ – частота и длина волны излучаемого сигнала; e и m – заряд и масса электрона; L – расстояние от КА до перицентра линии "передатчик–приемник" (рис. 1); V = dhr/dt – вертикальная компонента скорости КА; hr(t) – прицельный параметр линии "передатчик–приемник"; p(t) – прицельный параметр радиолуча; Xf(t) – рефракционное изменение мощности сигнала, определяемое из частоты сигнала f(t); N(h) – высотный профиль электронной концентрации; hi – верхняя граница ионосферы.
Погрешность формул (1)-(5) при моделировании радиопросвечивания сферически-симметричной среды не превышает искажений, возникающих из-за шума в данных радиозатменных экспериментов, если выполняются условия λ<35 см, L<104 км, |x(t)|<10-3, |n(h)–1|<10-4 [19,24]. В лучевом приближении решение обратной задачи радиопросвечивания, основанное на преобразовании Абеля для соотношения (1), достаточно точно определяет вертикальный профиль N(h) по вариациям f(t) [19-24].
При заданной стабильности бортового генератора инструментальные флуктуации f(t) нарастают с уменьшением длины радиоволны и точность определения N(h) ухудшается. С увеличением длины зондирующей радиоволны, во-первых, усиливаются вариации амплитуды и фазы поля в силу частотной зависимости диэлектрической проницаемости плазмы, а во-вторых, могут появиться дифракционные эффекты и приближение геометрической оптики окажется некорректным. На больших дистанциях L между КА и ионосферой при λ=32 см разномасштабные ионосферные структуры создают условия для образования многолучевости и каустик, что может привести к недостоверной интерпретации радиозатменных данных [20,21]. В связи с этим, расчет радиополя при моделировании целесообразно проводить с учетом дифракционных эффектов.
На существенное влияние дифракции радиоволн в радиозатменном эксперименте впервые было обращено внимание в работе [25], в которой проведено моделирование дифракции радиоволн на атмосферных структурах методом множественных фазовых экранов и выполнена реконструкция вертикального профиля температуры атмосферы с пространственным разрешением в десятые и сотые доли размера зоны Френеля. В дальнейшем техника множественных фазовых экранов широко применялась при анализе данных радиопросвечивания, в частности, в работе [26] впервые проводились оценки влияния мелкомасштабных хаотических структур (атмосферной турбулентности). Однако ни в одной из этих работ [25,26] нет практических оценок точности применяемого численного метода.
В работах [27,28] впервые проведено моделирование радиозатменного эксперимента путем решения параболического уравнения дифракции с помощью конечно-разностной схемы Кранка-Николсона [29], условия сходимости этой схемы хорошо известны и проверены на практике [27,28]. В данной работе при расчетах распределения поля также применяется прямое численное решение параболического уравнения:
Здесь координата x выделена направлением распространения первичной волны с волновым числом k; ортогональная координата y определена в плоскости, проходящей через центр планеты; проницаемость ионосферы ε(х,у) входит множителем при искомой комплексной амплитуде поля u; влияние атмосферы и поверхности планеты не учитывается.
Для параболического уравнения дифракции (6) решалась краевая задача в прямоугольной полосе, ориентированной параллельно направлению падения зондирующей волны (рис. 1). Рассматривалось только влияние сферически симметричной ионосферы, а влияние поверхности планеты и нейтральной атмосферы Венеры на радиополе исключалось. Отражения от боковых границ полосы (6050...6550 км от центра планеты) не достигают области локализации информативной части поля волны при достаточно протяженной ширине полосы, и на боковых границах ставилось условие идеального согласования с открытым пространством [30], обеспечивающее отсутствие отражения от границ. Кроме того, на боковых границах ставилось второе граничное условие, согласованное с распространением невозмущенной зондирующей волны вдоль боковых границ в свободном пространстве: равенство нулю нормальной к границе производной поля u(x,y). Наш подход полностью аналогичен типичной постановке краевой задачи для уравнения Шредингера [30], а использование неявной разностной схемы Кранка-Николсона для численного решения параболического уравнения апробировано на практике [27,28].
Принятая модель позволяет рассчитать стационарную структуру радиополя, формирующегося в результате прохождения плоской волны через сферически-симметричную ионосферу планеты. Из рассчитанных квадратурных компонент радиополя определяются функции P(t) и f(t), где t = h(t)/V, которые можно сравнивать с экспериментальными данными КА ВЕНЕРА-15,-16. Реальная и мнимая компоненты поля для разных излучаемых радиоволн (λ=32, 13 и 3.6 см) вычислялись с шагом 0.25 м вдоль волнового фронта и 10…20 м в направлении распространения в пределах всей области моделирования (полоса 0 <h< 500 км, длина полосы от 3 тыс. км до 40 тыс. км).
При расчетах применялась сферически-симметричная двумерная модель ионосферы Венеры, нижняя граница ионосферы 80 км, высота ионопаузы 350 км. Если задать модель среды табличной функцией, то разрывы производной показателя преломления среды могут привести к ложным эффектам и, следовательно, к большим ошибкам определения параметров поля. Специфических вычислительных сложностей не возникает, когда распределение электронной концентрации задано аналитической функцией. Поэтому в качестве вертикального профиля концентрации электронов N*(h) (рис. 2) использовали аналитическую аппроксимацию профиля N(h), полученного с помощью преобразования Абеля по вариациям частоты сигнала в эксперименте радиопросвечивания ионосферы Венеры 25.10.1983 г. [32]. Гладкий профиль N*(h) задавался суммой бесконечно дифференцируемых функций, формирующих слоистую структуру ионосферы Венеры, параметры которой адекватны экспериментальным данным [32]:
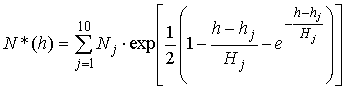 , (7)
, (7)
где Nj – концентрация в максимуме, hj – высота максимума, Hj – шкала высот j-го слоя, количество слоев j=10.
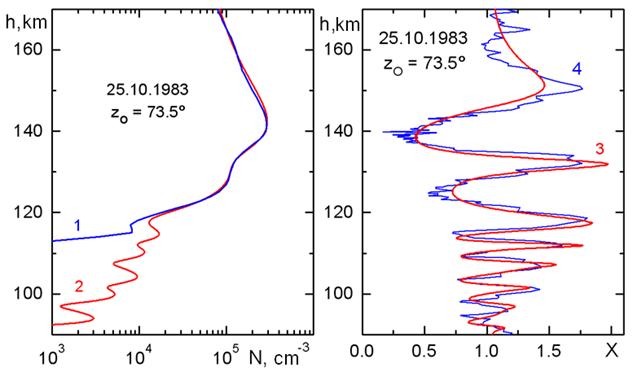
Рис. 2. Профиль N(h) (кривая 1), полученный из преобразования Абеля и профиль N*(h) (кривая 2), соответствующий экспериментальным данным: кривая 3 – результаты расчетов X(h) в лучевом приближении, кривая 4 – экспериментальная функция Xf(h) рефракционного изменения мощности сигнала λ=32 см в эксперименте радиопросвечивания ионосферы Венеры 25.10.1983 г.
Использование аналитической дифференцируемой функции N*(h) при моделировании радиопросвечивания устраняет ложные дифракционные эффекты, возникающие при резком изменении градиента электронной концентрации таблично заданной функции N(h). Более того, функция N*(h) точнее характеризует строение нижней ионосферы (80…120 км), чем функция N(h), полученная из экспериментальных данных с помощью преобразования Абеля. Итерационная процедура позволяет подобрать параметры слоев Nj, hj, Hj так, чтобы рефракционное ослабление мощности X(t), вычисленное по соотношениям (1)-(4) для сферически симметричной ионосферы с вертикальным профилем N*(h), было адекватно экспериментальной функции Xf(h), вычисленной по частоте сигнала f(h) на основе соотношения (5).
Результаты сравнения функций N*(h) и N(h), а также функций Xf(h) и X(h) представлены на рис. 2. Распределение электронной концентрации в нижней части ионосферы (рис. 2 кривая 2), невозможно найти традиционной методикой решения обратной задачи радиопросвечивания [33-35]. Нижняя граница профиля N(h) (кривая 1), полученного с использованием соотношений (1-4) и преобразования Абеля, находится на высоте 112 км, в то время как профиль N*(h) (кривая 2) демонстрирует наличие нижних ионизованных слоев. Указанием на существование таких слоев является корреляция (~0.8) между результатами расчетов функции X(h) в лучевом приближении (кривая 3) и экспериментальной функцией Xf(h) (кривая 4) [17-19].
Тонкие слои вблизи нижней границы ионосферы создают условия, при которых лучевое приближение может оказаться малодостоверным. Метод прямого численного решения параболического уравнения позволяет получить характеристики радиополя P(t) и f(t) и в области, где справедливо лучевое приближение, и в окрестности каустик, где эффекты дифракции и многолучевости радиоволн искажают результаты геометрооптической интерпретации радиозатменных данных. Основной задачей моделирования являлся анализ природы обнаруженных в эксперименте периодических вариаций мощности сигнала [19], которые могут оказаться дифракционной картиной радиополя, а не периодической структурой тонких слоев плазмы. Результаты моделирования определят область применимости лучевого приближения при распространении радиоволны через тонкие ионизованные слои нижней части ионосферы Венеры и позволят найти надежный критерий для выявления по экспериментальным данным нарушений лучевого приближения в случае, когда вертикальный размер слоистых структур сравним по величине с Френелевским радиусом радиолуча.
2. Результаты моделирования
На рис. 3 представлен пример распределения амплитуды радиополя с длиной волны 32 см, возмущенного зондируемой ионосферой. При отсутствии возмущений радиополе однородное, его амплитуда, нормированная к 1, соответствует серому цвету. Уменьшению амплитуды поля соответствуют градации серого цвета вплоть до 0 (черный цвет). Увеличению амплитуды поля соответствуют градации серого цвета вплоть до максимальной амплитуды в области образования каустик (белый цвет).
Уменьшение сечения лучевой трубки вследствие рефракции радиоволн приводит к возрастанию амплитуды поля. Концентрация или фокусировка поля вблизи каустик в лучевом приближении стремится к бесконечности, что приводит к необходимости учета дифракционных эффектов в окрестности каустик. Для радиоволны λ=32 см область каустик находится на расстоянии L > 20000 км (рис. 3), т.е. достаточно близко к траектории движения КА ВЕНЕРА-15,-16 (~11000 км), поэтому интерпретация радиозатменных данных требует тщательного анализа. Для радиоволн λ=13 см и 3.6 см расстояние до области каустик превышает 50000 км, т.е. каустики находятся далеко от траектории КА, следовательно, дифракцией на крупномасштабных неоднородностях можно пренебречь.
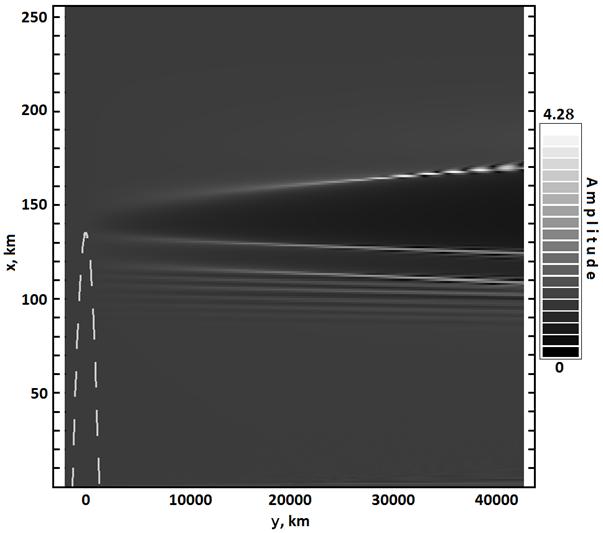
Рис. 3. Распределение амплитуды
радиополя (длина волны 32 см), возмущенного зондируемой ионосферой
Венеры.
Черный цвет – минимальная амплитуда, белый цвет – максимальная
амплитуда.
Рассмотрим вариации параметров поля при приближении трассы КА к области каустик. Будем считать, что бортовой приемник обладает достаточно высокой частотой дискретизации, позволяющей определить характеристики поля с очень высоким разрешением. При моделировании полагалось, что частота дискретизации 500 Гц и при скорости КА ~6 км/с характеристики поля u(t) усреднялись в интервале высот ~12 м. В реальных экспериментах частота дискретизации не превышает 50 Гц, поэтому дифракционные искажения измерений P(t) и f(t) сглаживаются сильнее, чем в наших расчетах.
На рис. 4 представлены вариации фазы φ(h) регистрируемых сигналов с разными длинами волн λ=3.6, 13, 32 см (здесь и далее h=Vt). Вариации фазы φ(h) радиоволны λ=3.6 см при L=3000 км и L=17000 км почти совпадают (кривая 1), что обусловлено малой рефракцией высокочастотной волны. Для радиоволны λ=13 см рефракция увеличивается, но различие фаз φ(h) при L=3000 км и L=17000 км (кривые 2,3) в данном масштабе малозаметно. Угол рефракции радиоволны λ=32 см достигает величины 10-4 рад, фазовый фронт заметно искривлен, поэтому функции φ(h) при L=3000 км (кривая 4), 11000 км (кривая 5), 23000 км (кривая 6) различаются, наибольшее различие наблюдается в областях быстрого изменения φ(h), где искривление фазового фронта максимальное. Следует отметить, что на вариациях фазы слоистые структуры нижней ионосферы и какие-либо очевидные признаки многолучевости или дифракции практически незаметны.
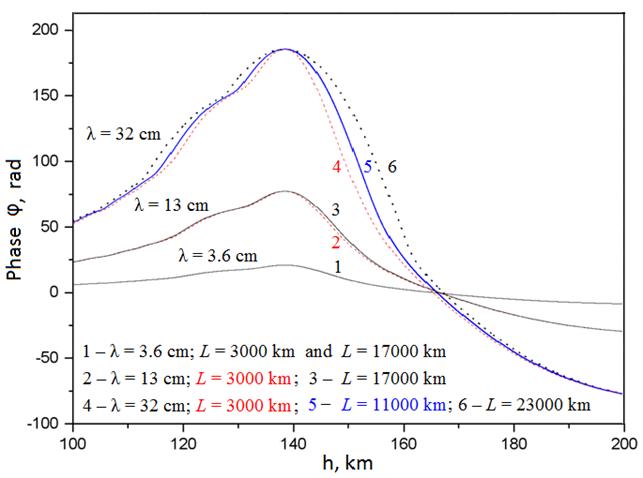
Рис. 4. Вариации фазы φ(h) регистрируемых
сигналов с разными длинами волн λ=3.6, 13, 32 см
при значениях L в
диапазоне от 3 103 до 23 103 км.
На рис. 5 представлены вариации частоты f(h) моделируемых сигналов с длинами волн λ=3.6, 13, 32 см. Функции f(h) радиоволны λ=3.6 см при L=3000 км и L=17000 км в данном масштабе (рис.5 кривая 1) не различаются, что обусловлено малой рефракцией высокочастотной волны. Вследствие малой рефракции влияние периодических структур нижней ионосферы (h<120 км) на вариации частоты f(h) незначительное, поэтому в реальном эксперименте влияние таких слоев будет маскироваться инструментальным шумом и обнаружение слоев окажется невозможным.
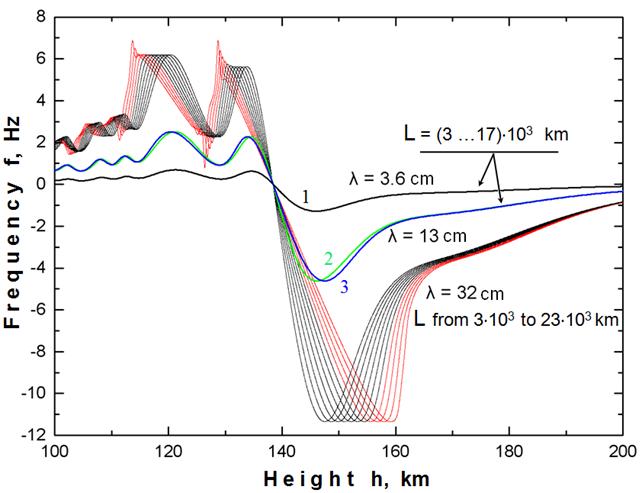
Рис. 5. Вариации частоты f(h)
регистрируемых сигналов с разными длинами волн λ=3.6, 13, 32 см
при
значениях L в диапазоне от 3 103 до 23 103 км.
Для радиоволны λ=13 см рефракционные эффекты увеличиваются, появляется небольшое различие функций f(h) при L=3000 км и 17000 км (кривые 2,3 рис. 5), четко выделяются периодические вариации функции f(h) при h<120 км. Амплитуда колебаний f(h) относительно тренда частоты в нижней ионосфере составляет 0.25 Гц и такие эффекты могут быть обнаружены в эксперименте при достаточно низком уровне (~0.05 Гц) инструментальных и иных случайных флуктуаций частоты.
Для радиоволны λ=32 см на рис. 5 представлены 11 функций f(h), для которых L изменяется от 3000 км до 23000 км с шагом 2000 км. В лучевом приближении значения экстремумов на функции f(h) определяются, главным образом, величиной вертикального градиента концентрации электронов и скоростью перемещения КА, поэтому изменение параметра L почти не влияет на значения экстремумов функции f(h) при L<15000 км. На рис. 5 видно, что при L>17000 км появляется аномально сильная зависимость экстремальных значений f(h) от параметра L на высотах 112<h<135 км, что свидетельствует о нарушении лучевого приближения при распространении радиоволны λ=32 см в области нижнего максимума ионизации дневной ионосферы Венеры. При зондировании слоистых структур нижней части ионосферы (h<112 км) аномальных искажений функции f(h) не наблюдается, т.е. нарушения лучевого приближения для L<15000 км незаметны.
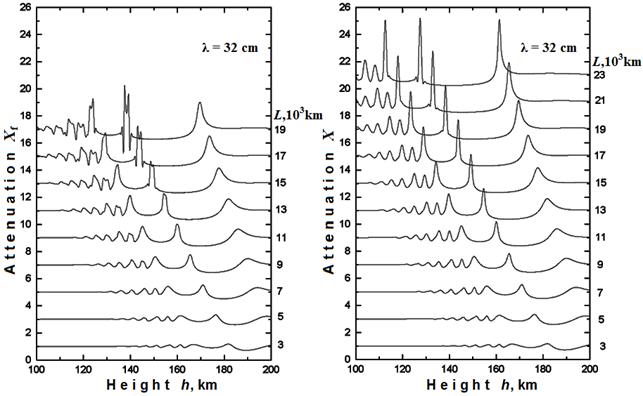
По частоте радиосигнала f(h) в лучевом приближении можно определить рефракционное изменение мощности Xf(h), используя соотношение (5). На рис. 6 представлены 9 функций Xf(h), для которых L изменяется от 3000 км до 19000 км с шагом 2000 км. Вариации рефракционного изменения мощности Xf(h) в сеансах радиопросвечивания дневной ионосферы Венеры имеют качественно одинаковый характер. В верхней части ионосферы выше 200 км отклонение Xf(h) от уровня 1 незначительные, при монотонном увеличении градиента электронной концентрации в процессе погружения луча наблюдалось бы монотонное увеличение Xf(h), но слоистые структуры вызывают колебания Xf(h). Четко выраженные вариации Xf(h) появляются при зондировании ионосферы Венеры ниже 200 км, где скорость изменения электронной концентрации на границах слоистых структур достигает максимальных значений, что приводит к сильному сжатию или расширению лучевых трубок и, следовательно, к значительным по величине вариациям мощности сигнала, о которых свидетельствуют экстремумы функции Xf(h).
В лучевом приближении увеличение девиации Xf(h) пропорционально увеличению параметра L, как это следует из (5). На рис. 6 при L=15000 км появляются искажения функции Xf(h) превышающие 1%, свидетельствующие о нарушении лучевого приближения в области высот 112…135 км. При L>15000 км нарушается пропорциональность между L и Xf(h), появляются дополнительные экстремумы функции Xf(h) на высотах 112…135 км, кроме того, становятся заметными искажения Xf(h) в нижней ионосфере (h<112 км) превышающие 1%. При L>19000 км аномальные флуктуации функции Xf(h) ниже 140 км достигают 100%, что обусловлено дифракцией радиоволн и неприменимостью соотношения (5) для определения рефракционного изменения мощности сигнала.
|
Рис. 6. |
Рис. 7. |
|
|
|
Изменение мощности X(h) радиоволны λ=32 см, полученное численным решением параболического уравнения (6), представлено на рис. 7, параметр L изменяется от 3000 км до 23000 км с шагом 2000 км. При L <4000 км колебания X(h) в нижней ионосфере (h<112 км) сопоставимы по величине с инструментальным шумом реального эксперимента (>2%), поэтому слоистые структуры трудно будет идентифицировать. Оптимальным для исследования нижней ионосферы является диапазон 5000 < L <17000 км, где вариации X(h) существенно выше уровня шума и в лучевом приближении они нарастают пропорционально увеличению параметра L. При L > 17000 км появляются аномальные экстремумы функции X(h) на высотах 112…135 км превышающие 1%, но искажения X(h) в нижней ионосфере (h<112 км) незначительные.
Сравнение данных рис. 6 и рис. 7 показало, что при L <15000 км функция X(h) совпадает с функцией Xf(h), полученной из соотношения (5), различие меньше 0.1%. Следовательно, совпадение вариаций X(h) с вариациями Xf(h) может служить критерием применимости геометрической оптики при анализе данных радиозатмений [17-19]. При L > 15000 км появляются различия между функциями X(h) и Xf(h) превышающие 1%, разность |X(h)–Xf(h)| резко увеличивается с ростом L. Расхождения между X(h) и Xf(h) свидетельствуют о неприменимости соотношения (5), следовательно, несовпадение вариаций X(h) и Xf(h) является надежным индикатором влияния эффектов многолучевости и дифракции радиоволн.
На рис. 8 представлено рефракционное изменение мощности X(t) радиоволны λ=13 см для параметров L от 3000 км до 17000 км с шагом 2000 км (кривые 1-8), а также функция X(t) для радиоволны λ=3.6 см при L=17000 км (кривая 9), полученные численным решением параболического уравнения (6). Малые колебания X(t) в нижней ионосфере (h<112 км) не будут обнаружены в реальном эксперименте для радиоволны λ=3.6 см при любых значениях L. Для радиоволны λ=13 см при L <7000 км колебания X(t) в нижней ионосфере сравнимы по величине с инструментальными шумами (>2%), поэтому будет трудно выделить ионосферные эффекты на фоне шума при анализе экспериментальных данных. Следует также отметить, что для радиоволн λ=13 и 3.6 см функция Xf(h), полученная из соотношения (5), совпадает с функцией X(h) при всех параметрах L в диапазоне 3000<L<17000 км, различие меньше 0.1%, что подтверждает справедливость соотношения (5) при разных условиях проведения радиозатменного эксперимента.
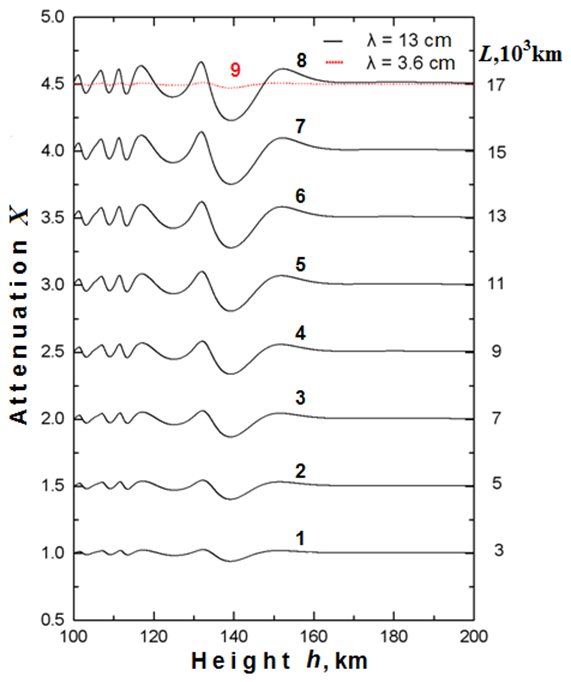
Рис. 8. Рефракционное изменение мощности X(t) радиоволны λ=13 см для L от 3000 км до 17000 км с шагом 2000 км (со смещением 0.5 единицы), а также функция X(t) для радиоволны λ=3.6 см при L=17000 км (кривая 9), полученные численным решением параболического уравнения (6).
Таким образом, результаты моделирования демонстрируют линейную связь между мощностью сигнала и изменением его частоты при зондировании сферически симметричной ионосферы монохроматической высокочастотной радиоволной, если выполняется лучевое приближение. Нарушение такой связи может быть обусловлено не только влиянием шума или асимметрии ионосферы, но и появлением дифракционных эффектов при распространении радиоволн в неоднородной среде.
3. Обсуждение результатов
Периодические колебания мощности сигнала (λ=32 см) в нижней ионосфере Венеры впервые были обнаружены в 2007 г. при более точной обработке данных радиозатмений КА ВЕНЕРА-15,-16 [17-19]. Разработанный метод диагностики слоистых структур [19] указывал на применимость лучевого приближения для интерпретации данных, что позволило авторам работы [18] сделать вывод о существовании нижней ионизованной области на высотах 80…115 км в дневной ионосфере Венеры. Стратифицированные слои нижней ионосферы не являются стационарными, их структура в разных сеансах разная, в отдельных сеансах формируются периодические по высоте слоистые структуры. Поэтому оставались сомнения, основанные на том, что осцилляции мощности зондирующего сигнала могли отражать дифракционную структуру поля, возникшую при распространении радиоволны в среде с узкими ионизованными слоями, на границах которых градиент электронной концентрации достаточно большой. Сомнения подкреплялись тем, что аналогичные ионизованные структуры ниже 115 км не обнаруживались ни в одной миссии к Венере.
Результаты нашего моделирования показали, что зондирующий сигнал с длиной волны λ=3.6 см вряд ли можно использовать для изучения нижней ионосферы Венеры. При любых условиях проведения эксперимента вследствие очень малой рефракции радиоволны влияние периодических структур нижней ионосферы (h<120 км) на вариации частоты f(h) и мощности P(t) будет маскироваться случайными флуктуациями параметров сигналов, обусловленных ограниченной стабильностью бортовой аппаратуры.
Из результатов нашего моделирования следует, что при благоприятных условиях проведения радиозатмений (высокая стабильность аппаратуры, расположение трассы КА достаточно далеко от ионосферы, малое влияние среды за пределами ионосферы на трассе связи с КА) результаты зондирования сигналом с длиной волны λ=13 см могут обнаруживать нижнюю ионосферу Венеры. Действительно, нижние ионизованные слои в ионосфере Венеры были обнаружены в эксперименте с КА VENUS-EXPRESS [12] на основе традиционной методики, использующей преобразование Абеля для определения электронной концентрации. Однако нижние ионизованные слои проявлялись очень редко (~10% сеансов) и авторы работы [12] предложили гипотезу о метеорной природе таких слоев.
Тщательный анализ большой серии радиозатменных экспериментов с КА ВЕНЕРА-15,-16 [19] с применением нового метода диагностики показал регулярное формирование многослойных ионизованных слоев с вертикальным масштабом 5…10 км на высотах от 80 до 115 км в дневной ионосфере и отсутствие подобных слоев в ночной ионосфере Венеры. Такое поведение ионизованных слоев трудно объяснить метеорной ионизацией. Природа образования многослойных структур в нижней ионосфере не выявлена, т.к. в области фотохимического равновесия модельные расчеты указывали на отсутствие заряженных частиц ниже 115 км [36,37]. Поэтому наше исследование было направлено на исключение возможности неправильной интерпретации результатов зондирования радиоволной λ=32 см.
Результаты моделирования показали, что вариации фазы радиосигнала малоинформативны, т.к. на вариациях фазы слоистые структуры нижней ионосферы и какие-либо очевидные признаки многолучевости или дифракции практически незаметны. Хорошим индикатором для выявления слоистых структур в нижней ионосфере являются вариации частоты и мощности сигнала, но дифракционные эффекты на функциях f(t) и X(t) выражены нечетко, если пересечение френелевских объемов радиолучей малое. В таких случаях элементарный критерий, основанный на сравнении размеров неоднородности с зоной Френеля, не дает однозначного ответа на вопрос о применимости геометрической оптики, т.к. диаметр зоны Френеля и размер неоднородностей среды сравнимы по величине. Оптимальным методом для анализа применимости лучевого приближения является вычисление функции Xf(t) из соотношения (5), т.к. искажения на функции Xf(t) выявляются на самой ранней стадии интерференции сфокусированных радиолучей.
Совпадение функции Xf(t) с X(t) наблюдалось при моделировании на разных длинах волн, когда не нарушалось лучевое приближение, что доказывает справедливость соотношения (5). Расхождения между X(t) и Xf(t) превышающие 1% появлялись на ранней стадии нарушения лучевого приближения. Следовательно, несовпадение вариаций X(h) и Xf(h) является надежным индикатором влияния эффектов многолучевости и дифракции радиоволн, а совпадение функций X(t) и Xf(t) может являться критерием применимости соотношений (1)-(5) для анализа данных радиозатмений. Наличие такого критерия позволяет оценивать достоверность экспериментальных результатов при решении обратной задачи радиопросвечивания.
Отсутствие дифракционных искажений функций Xf(t) и X(t) в модельных расчетах при L<12000 км подтвердило существование периодических колебаний показателя преломления венерианской ионосферы, обнаруженных по экспериментальным данным Xf(t) (кривая 4 на рис. 2). Выполненный анализ результатов моделирования указал на применимость лучевого приближения при радиозатмениях КА ВЕНЕРА-15,16 и, следовательно, на достоверность формирования многослойного высотного профиля электронной концентрации, представленного на рис. 2 (кривая 2). Не исключено, что такие периодические колебания электронной концентрации могут быть следствием волнового процесса, распространившегося из атмосферы до ионосферных высот.
Выводы
Проанализированы условия появления дифракционных искажений поля и возможность применения геометрической оптики при интерпретации данных радиопросвечивания тонких периодических слоев плазмы в ионосфере, выявлено, что производная частоты регистрируемого сигнала является наиболее чувствительным к появлению дифракционных эффектов параметром радиоволны. Методом численного решения параболического уравнения дифракции показано, что совпадение между вариациями мощности сигнала, регистрируемого спутником Венеры вдоль траектории движения, и рефракционным изменением мощности, рассчитанным по частоте зарегистрированного сигнала, может служить критерием применимости лучевого приближения при интерпретации радиозатменных данных. Выполнена валидация метода обработки данных радиозатмений спутников ВЕНЕРА-15,-16 и показана достоверность многослойных структур на профилях электронной концентрации в нижней ионосфере Венеры, полученных по вариациям мощности и частоты сигнала в процессе радиопросвечивания.
Авторы благодарят администрацию НИВЦ МГУ за предоставленный доступ к вычислительным ресурсам суперкомпьютерного комплекса СКИФ-ГРИД "Чебышев". Работа выполнена при частичной поддержке программы №22 Президиума РАН "Фундаментальные проблемы исследований и освоения Солнечной системы".
Литература
1. Lusignan B., Modrell G., Morrison A. et al. Sensing the Earth’s atmosphere with occultation satellites // Proc. IEEE. 1969. V. 57. N 4. P. 458.
2. Rangaswamy S. Recovery of atmospheric parameters from the Apollo/Soyuz-ATS-F radio occultation data // Geophys. Res. Letters. 1976. V. 3. N. 8. P. 483.
3. Liu A.S. On the determination and investigation of the terrestrial ionospheric refractive indices using Geos-3 / ATS-6 satellite-to-satellite traking data //Radio Sci. 1978. V. 13. N 4. P. 709.
4. D.D. Feng, B.M. Herman. Remotely Sensing the Earth’s Atmosphere Using the Global Positioning System (GPS)—The GPS/MET Data Analysis // Journal of atmospheric and oceanic technology, 16, 989 (1999).
5. Kursinski E.R., Hajj G.A., Schofield J.T., Linfield R.P., Hardy K.R. Observing Earth’s atmosphere with radio occultation measurements using the global positioning system // Journal of Geophysical Research. 1997. V. 102. D19. P. 23429-23465. doi:10.1029/97JD01569.
6. Kliore A., Gain D.L., Levy S. et al. Occultation experiments results of the first direct measurements of Mars atmosphere and ionosphere // Science. 1965. V. 149. № 3689. P. 1243-1250.
7. Kliore A.J., Levy G.S., Cain D.L., Fjeldbo, G., and Rasool, S.I. Atmosphere and ionosphere of Venus from the Mariner 5 S-band radio occultation measurements // Science. 1967. V. 158. № 3809. P.1683-1688.
8. Tyler. G. L. Radio propagation experiments in the outer solar system with Voyager // Proc. IEEE. 1987. V. 75. P. 1404-1431.
9. Brace L.H., Kliore A.J. The structure of the Venus ionosphere // Space Science Reviews. 1991. V. 55. Jan.-Feb. P. 81-163.
10. Jenkins, J.M., P.G. Steffes, D.P. Hinson, J. Twicken and G.L. Tyler. Radio occultation studies of the Venus atmosphere with the Magellan spacecraft: 2. Results from the October 1991 experiments // Icarus. 1994. V. 110. P. 79-94.
11. Арманд Н.А., Гуляев Ю.В., Гаврик А.Л., Ефимов А.И., Матюгов С.С., Павельев А.Г., Савич Н.А., Самознаев Л.Н., Смирнов В.М., Яковлев О.И. Результаты исследований солнечного ветра и ионосфер планет радиофизическими методами // Успехи физических наук. 2010. Т. 180. № 5. С. 542-548. URL: http://ufn.ru/ufn10/ufn10_5/Russian/r105j.pdf
12. M. Pätzold, S. Tellmann, B. Häusler, M. K. Bird, G. L. Tyler, A. A. Christou, P. Withers. A sporadic layer in the Venus lower ionosphere of meteoric origin // Geophysical research letters. 2009. V. 36. L05203.
13. Савич Н.А., Алтунин В.И., Андреев В.Е., Басос Ю.Ф., Богуславская Н.-Е.Е., Вышлов А.С., Гаврик А.Л., Дорощук О.Н., Кручкович М.М., Лясковская В.И., Молотов Е.П., Морской И.М., Набатов А.С., Овсянникова М.А., Селезнев В.В., Суханов К.Г., Шевердяев А.С. Двухчастотное радиозондирование кометы Галлея при пролете космических аппаратов Вега-1 и Вега-2 // Письма в Астрономический журнал. 1986. Т. 12. № 9. С. 675-682.
14. Pätzold M., Neubauer F.M., Andreev V.E., Gavrik A.L. Detection of the inner plasma pile-up region at comet Halley during the VEGA-1 flyby by the radio sounding experiment // Journal of Geophysical Research. 1997. V. 102. № A2. Р. 2213-2222. URL: http://www.agu.org/pubs/crossref/1997/96JA03140.shtml
15. Гаврик А.Л., Вышлов А.С., Дорощук О.Н., Конофалов В.П., Лаптев Н.В., Набатов А.С., Осмоловский И.К., Савич Н.А. Измерение вариаций интегральной электронной концентрации на трассах связи со станциями "Венера-13" и "Венера-14" // Космические исследования. 1983. Т. 21. № 3. С. 445-448.
16. Савич Н.А., Азарх С.Л., Вышлов А.С., Гаврик А.Л., Лаптев Н.В., Набатов А.С. Флуктуации частоты когерентных радиосигналов в околосолнечной плазме по данным аппаратов "Венера-15,16" // Космические исследования. 1987. Т. 25. № 2. С. 243-250.
17. А.Л. Гаврик, Ю.А. Гаврик, Л.Н. Самознаев. Неоднородная структура дневной ионосферы Венеры по данным радиопросвечивания при помощи станций Венера-15,-16 // Радиотехника и электроника. 2008. Т. 53. № 9. С. 1104-1111.
18. Gavrik A.L., Pavelyev A.G., Gavrik Yu.A. Detection of ionospheric layers in the Daytime Ionosphere of Venus at Altitudes of 80-120 km from VENERA-15 and -16 Two-Frequency Radio-Occultation Results // Geomagnetism and Aeronomy. 2009. V. 49. № 8. P. 1223-1225.
19. Гаврик А.Л., Гаврик Ю.А., Копнина Т.Ф., Самознаев Л.Н. Вариации амплитуд и частот когерентных радиосигналов при просвечивании дневной ионосферы Венеры // Радиотехника и электроника. 2010. Т. 55. № 3. С. 277-284.
20. Илюшин Я.А., Гаврик А.Л., Гаврик Ю. А., Копнина Т. Ф. Моделирование радиозатменного эксперимента методом численного решения параболического уравнения дифракции // Журнал радиоэлектроники: электронный журнал. 2012. № 3. С. 6-6. URL: http://jre.cplire.ru/jre/mar12/6/text.pdf
21. Ilyushin Ya.A., Gavrik, A.L. Simulation of the Venus ionospheric radio occultation experiment with the parabolic diffraction equation / 3th Moscow Solar System Symposium (3MS3). Moscow. Russia. 2012. P. 3MS3-PS-36. abst 210. URL: http://ms2012.cosmos.ru/sites/ms2012.cosmos.ru/files/3m-s3-abstracts.pdf
22. Савич Н.А., Андреев В.Е., Вышлов А.С., Гаврик А.Л., Климов В.В., Конофалов В.П., Лаптев Н.В., Мармулев В.А., Местэртон А.П., Набатов А.С., Осмоловский И.К., Самознаев Л.Н., Штерн Д.Я. Полярная ионосфера Венеры вблизи терминатора планеты по радиозатменным данным спутников "Венера-15,16" // Космические исследования. 1986. Т. 24. № 3. С. 448-454.
23. Гаврик А.Л., Самознаев Л.Н. Особенности дневной ионосферы Венеры в годы низкой и высокой активности Солнца // Космические исследования. 1987. Т. 25. № 2. С. 285-291.
24. Гаврик А.Л., Самознаев Л.Н. Анализ ошибок результатов радиопросвечивания дневной ионосферы Венеры, обусловленных ее несферичностью // Космические исследования. 1985. Т. 23. № 1. С. 148-157.
25. Karayel, T.E., Hinson, D.P. Sub-fresnel scale resolution in atmospheric profiles from radio occultation // Radio Science. 1997. V. 32. P. 411–423.
26. Gorbunov, M.E., Kirchengast, G. Processing X/K band radio occultation data in the presence of turbulence // Radio Science. 2005. V. 40. P. RS6001.
27. Ilyushin Ya.A. Fluctuations of the GPS signals on the tangential paths in the lower terrestrial atmosphere: influence of the small-scale structure // Journal of Atmospheric and Solar-Terrestrial Physics. 2008. V. 70. P. 1863-1869.
28. Илюшин Я.А., Захаров В.И. Влияние нерегулярных структур нижней атмосферы на распространение сигналов глобальных спутниковых радионавигационных систем // Радиотехника. 2009. № 3. С.84-91.
29. Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. - М.: Мир, 1972. - 418 c.
30. Baskakov V.A., Popov A.V. Implementation of transparent boundaries for numerical solution of the Schroedinger equation. // Wave Motion. 1991. V. 14. P. 123-128
31.
A.L. Gavrik, Yu.A. Gavrik, P. Withers, S. Joy. Venera 15 and 16 Radio
Occultation Ionospheric Electron Density Profiles. // NASA Planetary Data
System. 2010. Version 1.0, V15/V16-V-ROE-5-OCC-ELECTRON-DENS-V1.0.
URL:
http://ppi.pds.nasa.gov/search/view/?f=yes&id=pds://PPI/VROE_2001/CATALOG
32. Gavrik A.L., Gavrik Yu.A., Kopnina T.F., Kuleshov E.A. Oscillation of radio signal parameters near the lower boundary of the Venus ionosphere. / The third Moscow Solar System Symposium (3MS3). Moscow. Russia. Space Research Institute. 2012. P. 3MS3-PS-34. abst 208.
URL: http://ms2012.cosmos.ru/sites/ms2012.cosmos.ru/files/3m-s3-abstracts.pdf
33. А.Л. Гаврик, Ю.А. Гаврик, Т.Ф. Копнина, Е.А. Кулешов. Осцилляции вблизи нижней границы ионосферы Венеры по радиозатменным данным спутников "Венера-15",-16" // Радиотехника и электроника. 2013. Т. 58. № 10. С. 1013-1024.
34. Гаврик А.Л. Использование радиосигнала L диапазона в экспериментах двухчастотного радиопросвечивания // Журнал радиоэлектроники. 2011. № 8. С. 2-2. URL: http://jre.cplire.ru/jre/aug11/1/text.pdf
35. Гаврик А.Л., Гаврик Ю.А., Копнина Т.Ф. О возможности увеличения чувствительности метода радиопросвечивания // Журнал радиоэлектроники: электронный журнал. 2011. № 5. С. 3-3. URL: http://jre.cplire.ru/jre/may11/3/text.pdf
36. Gavrik A.L., Ivanov-Kholodny G.S., Mikhailov A.V., Savich N.A., Samoznaev L.N. The formation of the daytime Venusian ionosphere: the results of dual-frequency occultation experiments // Space Research. 1980. V. 20. P. 231-235.
37. Gavrik A.L., Savich N.A., Samoznaev L.N. The analysis of diffusion processes in the daytime ionosphere of Venus resting on the "Venera-9,-10" radio occultation data / Proceedings of the thirteenth international symposium on space technology and science. Japan. Tokyo. 1982. P. 1551-1555.