МОДЕЛИРОВАНИЕ АКСИАЛЬНО-СИММЕТРИЧНОГО МНОГОЗАЗОРНОГО РЕЗОНАТОРА

 

А. Н. Боголюбов, А. И. Ерохин, А. В. Шкитин

МГУ им. М.В. Ломоносова, физический факультет, кафедра математики

 

Статья получена 6 ноября 2014 г.

Аннотация. В данной работе предлагается математическая модель для расчета многозазорного аксиально симметричного резонатора. На основе предложенной модели произведен расчет собственных колебаний и собственных частот рассматриваемых систем.

Ключевые слова: атомарные функции, R-функции, многозазорный резонатор

Abstract. The mathematical model for computation of  multigap axial-symmetric resonator is developed in this paper. The computation of eigenvalues and eigenmodes of considered system on the base of developed model was carried out.

Key words: atomic functions, R-functions, multigapresonator.

Введение

В данной работе рассматривается аксиально-симметричный трехзазорный резонатор. Резонаторы подобного типа находят широкое применение при конструировании усилительных клистронов с распределённым взаимодействием в миллиметровом и субмиллиметровом диапазоне длин волн [1].

В общем случае поперечное сечение рассматриваемой системы может иметь достаточно сложную форму, поэтому в данной работе для его описания применяется метод R-функций, разработанный Рвачевым В.Л. и развитый Кравченко В.Ф. [2,3]. Данный метод позволяет построить такую числовую функцию, которая равна нулю на границе плоской области достаточно сложной формы.

В работе с помощью метода R-функций строится уравнение вида , состоящее из композиции элементарных функций, которое полностью описывает сечение резонатора. В зависимости от выбора R-функции она обладает некоторыми дополнительными свойствами, например, наперед заданной степенью гладкости, а также удовлетворяет различным типам граничных условий. При этом  внутри области  больше нуля, а вне области – меньше нуля [3].

Дополнительным преимуществом этого метода является общность математической постановки для большого класса сечений рассматриваемого резонатора [4].

Постановка задачи

            Рассмотрим трехзазорный цилиндрический резонатор с идеально проводящей поверхностью, поперечное сечение которого изображено на рис.1:

Рис.1 Поперечное сечение трехзазорного резонатора

 

Электромагнитные колебания в рассматриваемом резонаторе описываются  системой уравнений Максвелла:

                                              (1)

где  – волновой вектор,  и  – вектора электрической и магнитной напряженности поля.

На границе резонатора для касательной компоненты поля  выполняется граничное условие Дирихле:

где  – касательная компонента поля к поверхности резонатора, включая вырезы.

В данной работе ограничимся рассмотрением колебаний электрического типа, тогда поля  и  представимы с помощью поляризационного потенциала:

                                    (2)

                                                  (3)

где все компоненты потенциала, кроме направленной вдоль оси , равны 0 [5]. Подставим (2) и (3) в (1), получим:

                    

Раскрывая скобки и сокращая слагаемые справа и слева, получим уравнение Гельмгольца с граничными условиями Дирихле:

                                                      (4)

                                                               (5)

Представим z-компоненту  в следующем виде:

                                                    (6)

Получим:

Откуда:

                    (7)

Рассмотрим сначала уравнение для функции

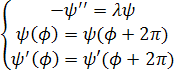                                        (8)

Отсюда получим :

,                                      (9)

Тогда для  получим уравнение:

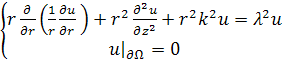                                     (10)

Проведя преобразование, аналогичное [6], получим следующую задачу:

Найти такие функции , которые удовлетворяют следующему уравнению для любых функций :

                  (11)

Численная реализация

Решение задачи представим в виде:

                                      ,                                           (12)

где  – R-функция Рвачева (Рис. 2), для построения которой использовались следующие логические операции [3]:

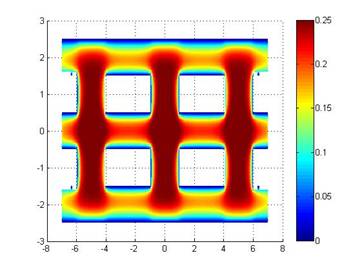
Рис.2.  – R-функция, описывающая сечение резонатора

Для поиска функции  будем использовать метод Галеркина. В качестве базисных функций выберем полную систему   сдвигов и сжатий атомарной функции , (рис.3), которая с хорошей точностью позволяет приблизить искомую функцию [7]:

                                          (13)

 

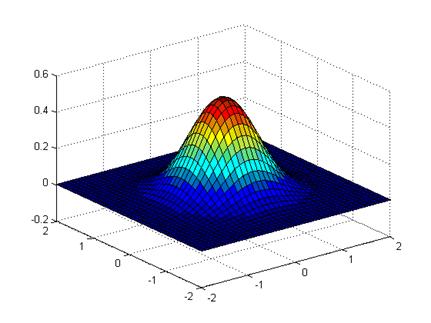
Рис.3

 

АФ  обладает следующими важными свойствами [3]:

1.     Одномерная функция  является бесконечно дифференцируемой финитной функцией с носителем  .

2.     АФ  связана с АФ . Эта связь может быть выражена следующим образом:

                    (14)

При :

                                                   

При :

                                              

                                                               

                

                                                               

                                                         

                                                         

3.     В точках вида  функция  принимает рациональные значения, которые могут быть точно вычислены по формуле:

                                     (15)

                                                                           

                            

                                          

                                

Из свойств  2, 3 следует, что значения функции  в точках вида  принимает рациональные значения, которые могут быть найдены с помощью формулы (15) для функции .

Так как функция  должна удовлетворять однородным граничным условиям, представим  в виде:

                                                           (16)

и подставим в (11). Получим:

           

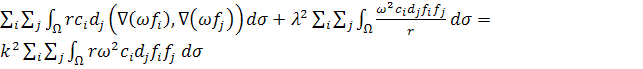
Введем следующие обозначения:

                                       (17)

                                                    (18)

                                            (19)

 

Учитывая, что равенство должно выполняться для любых наборов , получим следующую матричную задачу:

                                                      (20)

 – столбец неизвестных коэффициентов разложения, а  – симметричные ленточные матрицы.

 Результаты

Ограничимся рассмотрением колебаний, не зависящих от индекса m, то есть .

На основе рассмотренной математической модели был реализован алгоритм расчета собственных колебаний и собственных частот трехзазорного аксиально-симметричного резонатора с сечением, изображенным на рис. 1.

Параметры резонатора были выбраны следующие: длина =15 мм, высота =5 мм. Размер металлической  вставки: длина =2 мм, ширина =1 мм.

Расстояние по горизонтали между металлическими вставками  мм, расстояние по вертикали между металлическими вставками  мм.

В качестве теста программы проводился расчет собственных мод беззазорного резонатора, то есть цилиндра. Для данной задачи существует аналитическое решение, которое с высокой точностью совпадает с решением, полученным с помощью написанной программы. При увеличении количества базисных функций наблюдается быстрая сходимость алгоритма.

В качестве результатов работы программы были получены первые гармоники и соответствующие им распределения полей в указанном трехзазорном резонаторе.

Нормируя скорость света , получим первую собственную частоту . Соответствующая собственная мода и распределение  и  компонент поля   показаны на рис. 4-6:

 

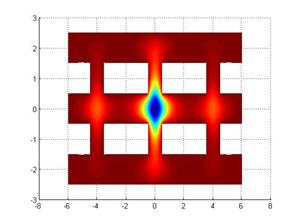
Рис. 4. Первая собственная мода  трехзазорного резонатора

 

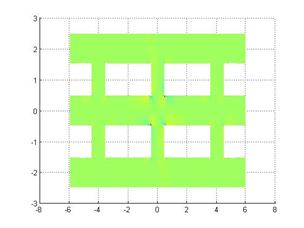
Рис. 5. Распределение компоненты  для первой собственной моды

 

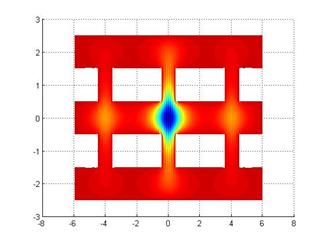
Рис. 6. Распределение компоненты  для первой собственной моды

 

Пятая собственная частота . Соответствующая собственная мода и распределение  и  компонент поля   показаны на рис. 7-9:

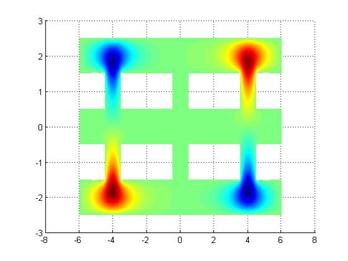
Рис.7. Пятая собственная мода  трехзазорного резонатора

 

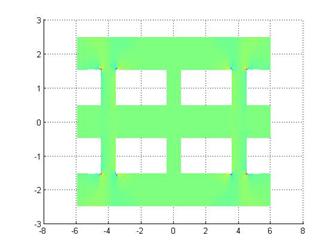
Рис. 8. Распределение компоненты  для первой собственной моды

 

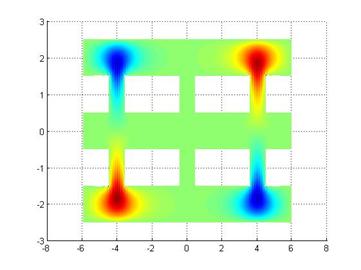
Рис. 9. Распределение компоненты  для первой собственной моды

 

Из рисунков 5 и 8 видно, что поля в углах имеют особенности, что хорошо согласуется с физикой данного процесса. [8]

 

Заключение

Был реализован математический пакет по расчету собственных колебаний и собственных значений трехзазорного резонатора. Благодаря реализации метода R-функций данную программу можно легко модернизировать для расчета сечений более сложных форм, в том числе для расчета резонаторов с любым количеством зазоров. В результате быстрой сходимости алгоритма данная модель может быть рекомендована для расчета конструкций подобного типа.

 

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-01-31397 мол_а, а так же гранта № 12-01-00479.

 

Литература

1. Фисенко Р.Н и др., «Резонаторная система для многолучевого клистрона», 13^th Crimean Conference «Microwave & Telecommunication Technology», 2003.

2. Рвачев В. Л., «Теория R-функций и некоторые ее приложения», Киев, изд. «Думка», 1982 г.

3. Кравченко В. Ф., Рвачев В. Л., «Алгебра логики, атомарные функции и вейвлеты в физических приложениях», Москва, изд. «Физматлит», 2006 г.

4. Кравченко В. Ф.,Басараб М.А., «Булева алгебра и методы аппроксимации в краевых задачах электродинамики», изд. «Физматлит», 2004 г.

5. Тихонов А.Н., Самарский Н. А., «Уравнения математической физики», М.: Изд-во МГУ, 1999 г.

6. А.Н. Боголюбов, А.И. Ерохин, И.Е. Могилевский, Н.Е. Шапкина, «Расчет резонансных частот открытого диэлектрического аксиально-симметричного резонатора с кусочно-постоянным радиусом», Вестник Московского Университета, Серия 3. Физика. Астрономия. 2009 г., №2, стр. 21-23.

7. Кравченко В.Ф. «Лекции по теории атомарных функций и некоторым их приложениям». Монография. – М.: Радиотехника, 2003

8. Боголюбов А.Н., Делицын А.Л., Могилевский И.Е., Свешников А.Г. Особенности нормальных волн неоднородного волновода с входящими ребрами // Радиотехника и электроника. 2003. Т.48. N7. C.787-794