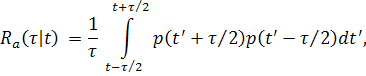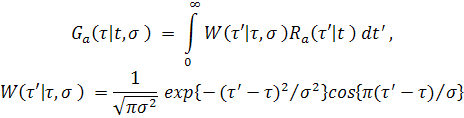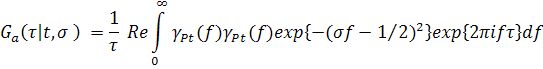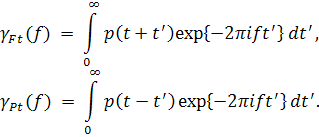УДК 004.383.3
Метод неинвазивного активного измерения артериального давления на основе согласованного с оценкой пульса управления датчиком
В. Е. Анциперов, Г. К. Мансуров
Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья поступила в редакцию 19 ноября 2015 г.
Аннотация. В работе представлены результаты разработки нового метода измерения нестационарных, квазипериодических сигналов медико-биологического типа, представителем которых является, в частности, сигнал пульсаций артериального давления. Показано, что предложенный метод компенсационного измерения динамических сигналов предполагает не только умные, но и активные датчики. В этой связи часть введения посвящена вопросам расширения концепции умных датчиков до парадигмы активных датчиков. Далее, вслед за вводным разделом по истории вопроса, приведено краткое описание принципов функционирования и некоторых конструктивных особенностей разработанного нами активного датчика. В связи с этим обсуждаются результаты тестирования и калибровки датчика и обосновываем необходимость достаточно сложного управления им. Оставшаяся часть работы посвящена вопросам возможных путей реализации такого управления и обосновывается выбранный нами путь. Обсуждается и обосновывается принцип компенсации пульсового давления на основе прогнозов паттернов пульсовой волны. Заключительный раздел посвящен техническим вопросам формирования динамических паттернов с помощью многомасштабного корреляционного оценивания текущего локального периода сердечных сокращений.
Ключевые слова: обработка медико-биологических сигналов, интеллектуальные датчики, активные датчики, активные измерения, компенсационные методы, неинвазивный мониторинг артериального давления, точечные процессы, широкополосные импульсные процессы, многомасштабный корреляционный анализ, аналитические спектры.
Abstract: The report presents the latest results of developing a new method of noninvasive continuous blood pressure monitoring. This method is based on the principle of pulse wave compensation. It is shown that sensors for such a measurement should be not only smart, but also active. In this connection, a part of introduction is devoted to the issues of expanding the concept of smart sensors to the concept of active sensors. A significant part of the report describes the technical designed of the active sensor for noninvasive pressure measurement. The results of its calibration and testing are under discussion. The main section of the report is devoted to the development of software for active sensor control – its intellectual stuffing. We describe and justify a new principle of managing active measurement of quasi-periodic processes – pulse wave compensation based on patterns forecast.
Key words: bio-medical signals processing; smart sensors; active sensors; active measurements, compensation method; noninvasive arterial blood pressure monitoring; point processes, wideband pulse processes, multiscale correlational analysis, analytic spectra.
Введение
Впечатляющий прогресс информационных технологий в компьютерной области, в сфере медийных устройств и в сфере средств коммуникации вселяет обоснованные надежды на аналогичные инновации в отношении медицинской техники, приборов и устройств. По этой причине в настоящее время оправданно возрос интерес к новым медицинским приборам, в особенности к компактным мобильным устройствам, так называемым гаджетам. Несомненно, их появление откроет новые возможности для здравоохранения, ориентированного на широкие слои населения. Кроме того, достоинством IT–ориентированной медицинской техники является ее мощный вычислительный потенциал, необходимый для реализации новых, аметодов измерения и обработки данных. В целом, можно уверенно сказать, что сегодня на практике сбывается предсказание отца кибернетики Норберта Винера о том, что вопросы связи и управления будут проникать во все сферы человеческой деятельности, включая биологию и медицину [1].
Отмеченный прогресс подразумевает ускорение темпов разработок и внедрения как принципиально новых медицинских технологий обследования пациентов, так и существенного пересмотра классических подходов. Одним из важных аспектов этой проблемы является задача развития информативных, эффективных и надежных методов измерения и обработки медико-биологических данных о пациенте. Отметим, что одной из основных тенденцией здесь, также как и в более широкой сфере разработок индустриальных систем мониторинга и контроля, является всестороннее внедрение интеллектуальных датчиков. Одной из основных задач последних является максимальная автоматизация измерений – соответственно минимизация роли человека в процессах измерения [2]. Важной чертой аппаратной реализации интеллектуальных датчиков является обязательное использование в них микропроцессоров (μP) и, как правило, беспроводных коммуникационных устройств (CU) для приема команд управления / передачи измеренных данных, см. Рис.1.
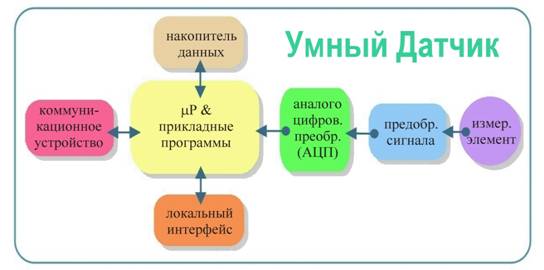
Рис.1 Принципиальная архитектура компонент интеллектуальных датчиков [2].
В данной работе мы приводим результаты исследований и разработок по интеллектуализации одного из популярных (если не самого популярного!) в медицине прибора – измерителя артериального давления (АД). Ниже в работе показано, что возможность добавления к классическому тонометру следящей системы, блока формирования на основе наблюдений прогноза динамики давления и гибкого управления в соответствии с прогнозом датчиком позволяет осуществлять мониторинг АД непрерывно во времени, практически без участия врача. Более того, удается неинвазивно измерять текущее давление в абсолютных единицах – в мм рт.ст.! Естественно, что все эти преимущества реализуются на базе встроенного микроконтроллера (μC) и его периферии – характерных атрибутов современных интеллектуальных датчиков, как это изображено на Рис.1. Однако в нашем случае для измерения давления предложенным нами компенсационным методом пришлось пойти еще на один шаг дальше – ввести петлю обратной связи согласованного с наблюдениями управления датчиком. В итоге сложилась концепция активного датчика, архитектура которого расширяет архитектуру интеллектуальных датчиков так, как показано на Рис.2.
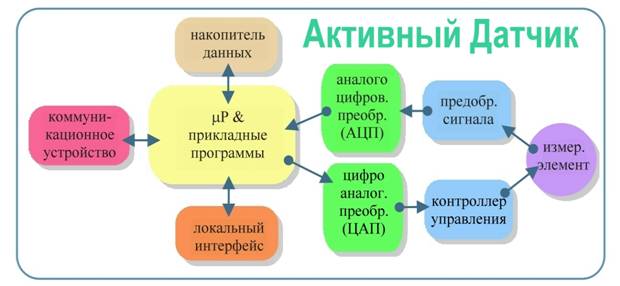
Рис.2 Принципиальная архитектура компонент активных датчиков.
Ниже, вслед за вводным разделом по истории вопроса, мы приводим краткое описание принципов функционирования и некоторых конструктивных особенностей разработанного нами активного датчика для измерения АД и обосновываем необходимость достаточно сложного управления последним. Сразу отметим, что приведенное ниже описание датчика не преследует цель изложения особенностей его инженерного решения, оно приводится как типичный пример для обсуждения проблемы активных измерений. Именно эта проблема находится в центре внимания работы и ее решению на основе концепции многомасштабного корреляционного анализа (МКА) [3,4] и техники аналитических спектров (АСП) [5,6] посвящена данная работа.
Эволюция подходов к измерению АД
Одним из первых (1876 г.) неинвазивных аппаратов, пригодных для измерения кровяного давления у человека, был изобретенный Э.Ж. Марием плетизмограф.
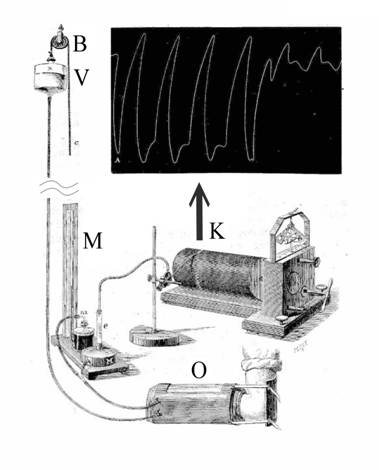
Рис.3 Аппарат Мария измерения АД : плетизмограф O
соединен с подвешенным на блоке B заполненным
водой резервуаром V
и с
ртутным манометром М; изменение объема записывалось на закопченной ленте К
соединенным с поплавком e пером
[7].
Работа плетизмографа основывалась на регистрации импульсов изменения объема конечности, связанных с пульсациями АД [7], Рис.3. При измерении предплечье пациента помещалось в заполненный теплой водой плетизмограф O. Изменение кровенаполнения артерий предплечья, связанное с толчками сердца (пульсом), приводило к вытеснению воды из плетизмографа, что в свою очередь перемещало поплавок и записывающее плетизмограмму перо (Рис.3). В эксперименте Мария изменения объема регистрировалось при постоянном давлении в плетизмографе, которое задавалось высотой подвешенного на блоке B резервуара с водой V и отображалось на последовательно подсоединенном манометре M.
В своих экспериментах Марий получил много интересных результатов, в частности, обнаружил зависимость размаха (амплитуды) плетизмограммы от величины давления в плетизмографе [7]. В принципе, на основе этих данных можно было бы, как стало известно позднее, определять оба главных показателя АД – как систолическое, так и диастолическое давления. Однако из-за сложности реализации и неоднозначной трактовки результатов плетизмографический метод Мария долго (около ста лет) не получал развития.
Сложилось так, что большего внимания в конце IX века удостоились методы измерения АД основанные на сфигмоманометрии – на наблюдениях за изменениями характера сердечного пульса («твердый пульс», «мягкий пульс» и т.д.), проявляющегося в микродвижениях стенок артерий. Основной задачей аппаратов – сфигмоманометров стало нахождение такого внешнего давления на артерию, которое бы уравновесило контрдавление крови, в результате чего кровоток бы прекратился и, соответственно, исчез пульс. Наиболее удачным из числа первых сфигмоманометров был аппарат Самюэля фон Баше, созданный им в 1881 г. С его помощью он, хотя и приблизительно, определял систолическое давление. Густав Гертнер в 1899 г. усовершенствовал этот тип аппарата и назвал его тонометром.
Кульминацией поиска способов неинвазивного измерения АД стали два открытия, обеспечившие возможность успехов кардиологических исследований в XX веке: описание сфигмоманометра Рива-Роччи [8] в 1896 г. и открытие тонов Короткова в 1905 г. Метод Рива-Роччи состоит в сжатии плечевой артерии с помощью специальной манжеты, соединенной с ртутным манометром. Воздух в манжету нагнетают с помощью баллона до тех пор, пока не исчезнет пульс, а затем его медленно стравливают. О величине АД судят по показаниям манометра в момент появления пульса. Таким образом, прибор позволяет оценить систолическое давление. Открытие Н.С. Коротковым в 1905г. закономерностей звуковых явлений при декомпрессии плечевой артерии легло в основу альтернативного метода определения систолического и диастолического АД. Считается, что тоны Короткова связаны с нарушением ламинарного течения крови по артериям при их пережатии. Это нарушение сопровождается ударными явлениями и звук этих ударов позволяет «услышать пульс» в диапазоне между систолическим и диастолическим АД.
Технический прогресс в области микроэлектроники и вычислительной техники позволил во второй половине XX века усовершенствовать ставшую классической методологию измерения АД Рива-Роччи и Короткова [9]. Усовершенствования в основном были связаны со стремлением максимально исключить влияние человеческого фактора на процесс измерения. При этом оказалось, что для автоматических процедур определения параметров АД наиболее удобной оценкой характера пульса является амплитуда осцилляций давления в окклюзионной манжете – факт, столетием ранее обнаруженный Марием! В 1976 г. был выпущен на рынок первый прикроватный автоматический измеритель АД (Dinamap825), реализующий модифицированный метод Мария. Переход от плетизмографа к обычной окклюзионной манжете, соединившей в себе устройство создания внешней компрессии и не очень точного, но приемлемого для задач измерения АД датчика пульсаций, положил начало новой, осциллометрической методике. На сегодняшний день доля автоматических и полуавтоматических измерителей АД на основе осциллометрического метода составляют около 80% всех аппаратов. Идет интенсивное соревнование производителей в области исследования алгоритмов обработки измеренных данных с целью повышения точности и надежности получаемых результатов. Последние модели приборов имеют повышенный “интеллектуальный уровень” (включая модели “fuzzi logic”) и их вполне можно отнести к категории интеллектуальных сенсоров (см. Рис.1).
Перечисленные методы предполагают одноразовое измерение параметров АД. Часто этого достаточно для общей оценки состояния сердечно–сосудистой системы. Однако существует много ситуаций требующих непрерывного наблюдения АД, буквально мониторинга АД от удара сердца к удару (beat-to-beat). В крайних случаях это осуществляется инвазивно, непосредственно внутри одной из периферийных артерий при введении в нее катетера. Однако, поскольку инвазивный способ связан с дискомфортом пациента и имеется риск осложнений при установке катетера, для рутинных наблюдений желательны неинвазивные методы.
Одно из первых решений в этом направлении было найдено Пеньязом. Методика его способа неинвазивного непрерывного измерения АД была описана в 1973 году и мотивировалась стремлением уменьшить связанные с артериальной катетеризацией риски и при этом сохранить преимущества непрерывного мониторинга артериального давления [10]. Пеньяз использовал метод объемной компенсации, основанный на идее "разгрузки стенок сосудов" (предполагается, что в “разгруженном” состоянии давление внутри сосудов равно давлению вне их). Основной элемент аппарата (Рис.4.А) представляет собой небольшую напалцевую манжету, содержащую источник света на одной стороне и ИК-приемник на противоположной, с их помощью по величине поглощения света оценивается объем крови в пальце. Сигнал, полученный от подобного “плетизмографа”, используется затем в цепи обратной связи для регулировки величины давления в манжете. Давление регулируется таким образом, чтобы поддерживать объем крови в пальце постоянным во времени, равным объему, который при калибровке выбран как "разгружающий" сосуды. При этом осцилляции регулирующего давления можно считать приблизительно равными давлению в артериях. Позже были предложены формулы для пересчета давления от артерий пальца к плечевым артериям, что позволило верифицировать метод по отношению к классическим процедурам.
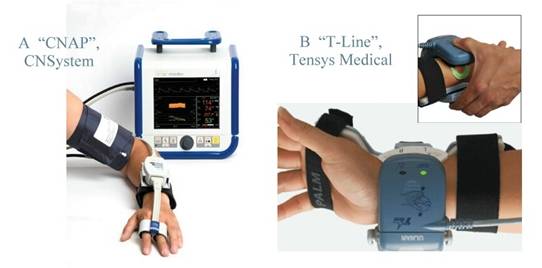
Рис.4
Современная аппаратура для неинвазивного непрерывного измерения АД :
A ̵ прибор “CNAP” на основе метода объемной
компенсации Пеньяза;
B
̵ прибор “T‑Line” на основе метода артериальной
тонометрии [9]
Другим известным решением, обеспечивающим неинвазивное непрерывное измерение АД, является артериальная тонометрия. В ней, как и в методе Пеньяза, оцениваются пульсовые осцилляции АД, но принцип "разгрузки стенок артерий" другой. В данном случае манжета располагается на запястье и содержит расположенный над лучевой артерией датчик тонометра (Рис.4.B). Датчик прижимает артерию к лучевой кости настолько, чтобы в достаточной степени ее сжать, сделать контакт с ее стенкой плоским (но не пережать до окклюзии). Затем через стенки сосуда с помощью тензодатчиков бокового давления регистрируется пульсовые изменения АД. Величина давления, необходимая для того, чтобы уплощить, но не закрыть артерию, известна как “рабочее усилие прижима” и рассчитывается по достаточно сложному алгоритму, который включает в себя предварительные оценки систолического, диастолического и пульсового давлений.
Упомянутые методы непрерывного измерения АД обладают рядом достоинств и недостатков, их детальное обсуждение можно найти, например, в работе [9]. С нашей точки зрения главным недостатком существующих неинвазивных методов является то, что вне зависимости от способов "разгрузки стенок сосудов", контроль разгрузки осуществляется в них на основе интегральных параметров (кровенаполнение, полная сила, действующая на датчик, смещение датчика как целого и т.д.). Это позволяет относительно неплохо отслеживать “усредненную” пульсовую волну АД, но не гарантирует передачи деталей формы импульса. Нами был предложен иной способ измерения АД, ориентированный на локальную разгрузку стенок артерий методом компенсации локального давления.
Неинвазивное непрерывное измерение АД методом компенсации пульсового давления
На основе анализа известных неинвазивных методов непрерывного измерения АД [9], можно прийти к выводу, что лучших результатов мониторинга нестационарной динамики АД удалось добиться при помощи так называемых компенсаторных или близких к ним методов.
Методы компенсации применяются в практике измерения различных физических величин и основаны на компенсации неизвестной измеряемой величины противодействующей управляемой величиной посредством сведением к нулю их разности. Простейшим примером служат чашечные весы, на которых неизвестный вес Wu измеряется с помощью набора разновесок (гирь) Wv (Рис.5(А)). Нуль-индикатором у весов служит заданное положение коромысла или связанной с ним стрелки.
Метод компенсации считается высокоточным, применяется для механических и электрических измерений, имеет варианты исполнения в виде мостовых и полумостовых схем (Рис.5(B,C)). В некоторых случаях, для повышения точности измерений при отклонениях физической величины от нуля меньше дискретности компенсатора, может использоваться калиброванная шкала нуль-индикатора. Отметим, что обычно метод компенсации применяется для измерения статических величин.
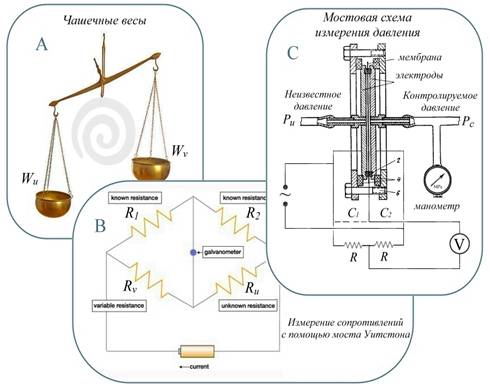
Рис.5
Измерение физических величин методом компенсации:
A - измерение веса предметов Wu с помощью чашечных весов;
B - мостовая схема измерения
неизвестного сопротивления Ru ;
С - измерение давления Pu в агрессивных средах посредством контроля
недеформированного состояния мембраны;
Нами метод компенсации был выбран в качестве принципиальной основы измерения меняющегося во времени артериального давления. Применение метода для измерения динамической величины стало возможным благодаря следующим обстоятельствам. Во-первых, АД меняется не столь уж быстро, его ритм составляет по порядку величины один удар в секунду, а спектр укладывается в несколько десятков Hz. А во-вторых, на сегодняшний день доступны относительно дешевые, высокопроизводительные микроконтроллеры (ATMEL, MICROCHIP, STMicroelectronics и пр.), для которых динамика АД представляет собой практически квазистатические изменения.
Как отмечалось выше, наш способ измерения АД ориентирован на локальную, без манжеты, разгрузку стенок артерий посредством компенсации контролируемым давлением внутриартериального. Отчасти он похож на метод мостового измерения неизвестного давления Pu подобный изображенному на Рис.5(С). Однако наш способ сочетает в себе также элементы динамического, подстраиваемого как в методе Пеньяза [10] управления компенсацией. Внешний вид разработанного нами прибора для непрерывного мониторинга АД и способ измерения им внутриартериального давления представлены на Рис.6.
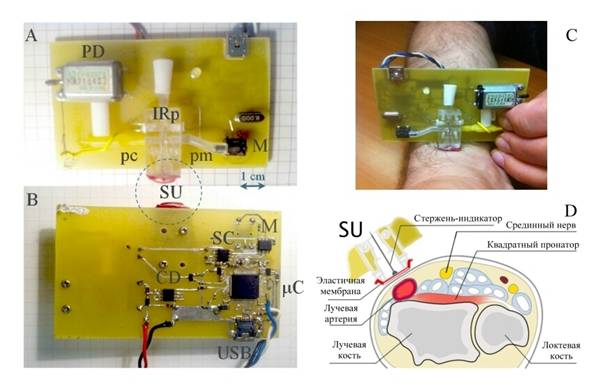
Рис.6.
Устройство активного датчика непрерывного измерения АД и способ измерения АД
методом компенсации:
A, B - внешний вид опытного экземпляра датчика - аппаратная (A) и микроэлектронная (обратная) стороны
платы прибора;
C, D - расположение измерительного
элемента датчика (SU) над лучевой
артерией -
фото приложенного к руке пациента датчика (C) и графический эскиз поперечного
сечения руки и датчика (D)
Отметим, что разработанный нами прибор (Рис.6(A,B)) в точности соответствует концепции активного датчика (см. выше, Рис.2). Главную роль в нем играет программируемый микроконтроллер μC (STM32L152RBT), имеющий с одной стороны коммуникационный вход/выход (USB), с другой связанные с измерительным элементом SU интерфейсы линий сигнала (pm) и управления (pc). В линии сигнала находится индикатор смещения мембраны SC и измеритель давления с инструментальным усилителем M, в линии управления – насос с электроприводом PD и микросхема управления двигателем CD. Обе линии, pm и pc, представляют собой трубчатые отведения от заполненной жидкостью полости измерительного элемента (SU), который представляет собой камеру с затянутым эластичной мембраной отверстием. К мембране одним концом прикреплен тонкий шток (Рис.6(D)). Другой конец штока частично перекрывает поток IR–излучения внутри оптоэлектронной пары IRp, реализуя тем самым индикатор деформационных смещений мембраны. При неравенстве давлений в камере SU и непосредственно за мембраной, последняя будет деформироваться в ту или другую сторону, перемещая шток в направлении деформации. Это перемещение приведет к изменению площади перекрытия им потока излучения IRp, которое и зарегистрируется индикатором смещения SC. Если подобрать давление в SU таким, что оно вернет мембрану в плоское, недеформированное состояние, то ввиду равенства давлений по обе стороны мембраны, тем самым будет измерено внешнее давление. Если SU уставлен непосредственно над лучевой артерией, как показано на Рис.6(C, D), то, полагая, что внешнее давление является артериальным, мы тем самым измеряем его значение. Это собственно и составляет содержание предложенного нами компенсационного метода измерения.
Приведенное качественное описание работы
датчика АД можно проиллюстрировать количественными результатами, полученными
нами в экспериментах с прибором. На Рис.7(А) приведена зависимость
деформационного смещения мембраны SU (в единицах АЦП индикатора
смещения SC) в ответ на равномерно со временем увеличиваемое давление
внутри SU при постоянном внешнем давлении (разность давлений на
мембране P есть отсчитываемые от атмосферного давления показания
M в mmHg). Из приведенных графиков следует, что при малых (±5 mmHg)
перепадах давлений по обе стороны мембраны сигнал индикатора смещения SC
оказывается также линейным, пропорциональным разности давлений. На Рис.7(B)
приведены аналогичные зависимости смещения мембраны SU и давления P внутри SU (отсчитываемого от атмосферного)
при компенсации равномерно увеличивающегося внешнего давления – с включенной
линией управления pc. Компенсирующее давление P создается насосом
при подаче на его двигатель PD напряжения с широтно-импульсной модуляцией, которое,
в свою очередь, формируется микросхемой CD. Не уточняя
детали механизма формирования, отметим, что результирующее P пропорционально
сигналу управления y, который микроконтроллер μC направляет CD в ответ на измеренное SC
смещение мембраны ε (и
предыдущие, запомненные значения). В качестве алгоритма управления изначально
был выбран алгоритм простейшего ПИД регулятора [11], управляющий сигнал 
которого в
момент времени (отсчет) j формируется
в соответствии с классической рекуррентной формулой:
|
(1) |
где 
–
предшествующий сигнал, 
– текущее
и предшествующие смещения мембраны от
нулевого положения, 
–
эмпирически подбираемые коэффициенты. Из приведенных графиков Рис.7(B) следует,
что в достаточно широком диапазоне изменений внешнего давления (10–170 mmHg)
с помощью ПИД-регулирования (1) удается удерживать мембрану SU вблизи положения равновесия.
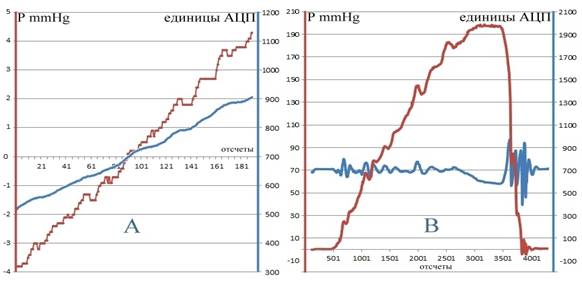
Рис.7. Динамика смещений мембраны SU (единицы АЦП) в ответ на изменяющуюся
со временем перепад давлений внутри и вне SU.
A - при
постоянном внешнем давлении (= атмосферному) и равномерно увеличивающимся
внутреннем P (mmHg);
B - с компенсацией равномерно увеличивающегося внешнего
давления внутренним P (~ PID, см. формулу (1) );
С учетом приведенных калибровочных данных были в большом количестве проведены эксперименты по собственно мониторингу артериального давления. Результаты одного из измерений представлены на Рис.8. Из приведенных графиков (нижняя часть рисунка) видно, что с помощью ПИД-регулирования удается в течение всего времени измерения АД удерживать мембрану вблизи недеформированного (плоского) положения. Качество такого регулирования можно оценить, если пересчитать величину малых отклонений мембраны от положения равновесия – своеобразного дрожания (jitter) мембраны – в пропорциональную им (см. Рис.7(А)), не скомпенсированную разность давлений. Для иллюстрации качества компенсации в верхней части Рис.8(А) приведены график давления P внутри камеры SU (данные измерителя давления M) и эти же данные скорректированные на пересчитанную по смещениям мембраны разность давлений (оценка АД). Видно, что в сравнении с самим P поправка не велика, давление P в среднем совпадает с оценкой АД, но в моменты быстрого изменения формы пульсовой волны регулятор не успевает эти изменения отслеживать.
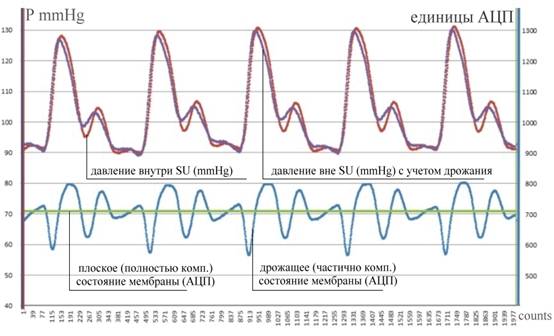
Рис.8. Динамика смещений мембраны SU (единицы АЦП) при компенсации переменного
во времени АД.
Внизу - дрожание сигнала SC около уровня, соответствующего
недеформированному состоянию мембраны (~ 700 ед. АЦП);
вверху ̵ данные измерителя
давления M внутри камеры SU P (mmHg) и скорректированная на
смещения мембраны оценка АД.
Общее впечатление от первых результатов по мониторингу АД с помощью описанного выше активного датчика оказывается двойственным. С одной стороны датчик решает поставленную перед ним задачу – с его помощью можно не только измерять главные показатели АД – систолическое и диастолическое давления (размах АД), но и наблюдать саму пульсовую волну, причем не с помощью косвенных измерений, а посредством измерения непосредственно давления (в мм рт.ст.)! С другой стороны, как можно было изначально предполагать, простой ПИД-регулятор не обеспечивает полной компенсации, что приводит к искажению деталей пульсовой волны. Кроме того, алгоритм компенсации на основе ПИД-регулирования (1) оказался на практике весьма сложным в вопросе настройки его параметров.
Управление компенсацией пульсового давления на основе паттернов пульсовой волны
Отмеченные недостатки, связанные с неполной
компенсацией переменного во времени артериального давления, имеют достаточно
простые объяснения. Во-первых, используемый ПИД- регулятор является достаточно
частным случаем класса линейных регуляторов, а известно [12], что линейные
методы обработки биологических сигналов и тем более линейные способы адаптации
к ним применимы только в ограниченных диапазонах изменений и при строго
контролируемых (например, лабораторных) условиях. Это объясняется тем, что из-за
высоко нелинейного, неравновесного характера живых систем, даже небольшие
изменения в их физиологическом состоянии могут приводить к большим изменениям в
результатах. Во-вторых, ПИД-регулирование учитывает только локальные
характеристиками сигналов – (1) линейно связывает производную управления с сигналом
смещения 
и его первой
и второй производными, как это принято в теории динамических систем. В случае
динамических систем такое регулирование естественно, поскольку основной чертой
таких систем является детерминированность. Однако живые системы и их
подсистемы, как известно, плохо описываются моделями динамических систем, даже при
свободе выбора коэффициентов соответствующих дифференциальных уравнений. Живые
системы в гораздо большей степени соответствуют моделям стохастических, недетерминированных
систем [12]. И, в-третьих, низкий порядок регулятора (1), предпочтительный
ввиду простоты его реализации [11] для ряда технических задач, является
недостатком для сложных биомедицинских сигналов, в частности, для сигнала АД. С
тем, чтобы проиллюстрировать последнее утверждение, приведем небольшой анализ
управления (1).
Для простоты предположим, что смещение
мембраны 
пропорционально
разности внешнего давления p и
давления P внутри
камеры SU: 
, а P
пропорционально сигналу микроконтроллера 
. Тогда в
силу (1) значения p и
P будут
связаны линейным соотношением:
|
(2) |
где коэффициенты A,B,…,E однозначно
выражаются через K, G и . Домножая
(2) на комплексную экспоненту 
, где 
– мнимая
единица, F –
удвоенная частота Найквиста, и суммируя по j в бесконечных пределах,
получим следующее соотношения между спектрами Sa(f)
и SP(f) внешнего и внутреннего давлений p и P :
|
(3) |
Из (3) следует, что спектр SP(f)
компенсирующего давления P формируется
умножением спектра внешнего давления p на
передаточную (transfer function) функцию некоторого фильтра
второго порядка. Известно [13], что в наиболее общей практической ситуации модуль
такой передаточной функции имеет пару симметричных максимумов в точках ± f0, где 
, а z0 – любой из двух комплексно-сопряженных
корней знаменателя. Другими словами, давление P отслеживает p только в некоторой
полосе частот с центром f0 . Параметры
этой полосы задаются подбираемыми коэффициентами ПИД-регулятора.
Естественно, что частота f0, на которую настраивается ПИД-регулятор, лежит вблизи частоты наиболее выраженного колебания пульсовой волны – частоты сердечного ритма или кратной ему. В любом случае компенсирующее давление P оказывается достаточно узкополосным сигналом. Однако форма пульсовой волны АД из-за имеющих место резких деталей имеет широкий спектр. Поэтому, из проведенного анализа следует очевидный вывод – низкий порядок регулятора принципиально не допускает высокоточного компенсирующего управления активным датчиком.
Повышение порядка регулятора (1) может частично улучшить качество регулирования, но все равно не решит задачу. Это связано с еще одним обстоятельством: пульсации АД, как впрочем, и колебания любого сигнала биологического происхождения, не представляют собой строго периодического процесса. Хотя и принято говорить о частоте пульса, частоте сердечных сокращений и т.д., под этими величинами обычно понимают не собственно (мгновенную) частоту, а усредненные за большие временные интервалы ее значения. Например, типичной единицей измерения сердечного ритма является число ударов в минуту. Мгновенная же частота за это время, как правило, сильно меняется. Обратная средней частоте величина – среднее время между ударами также имеет лишь косвенное отношение к интервалу времени между соседними импульсами АД. Относительное изменение длительности интервала между импульсами даже в норме меняется в течение минуты более чем на 10%, что известно как свойство вариабельности сердечного ритма [14]. Типичный пример вариабельности ритма представлен на Рис.10(А), где изображена динамика RR-интервала (измеренное по R-пикам время между соседними импульсами) на реальной ЭКГ записи.
Перечисленные факты указывают на то, что пульсовая волна АД в гораздо большей степени похожа на широкополосный импульсный сигнал (ШПИС), нежели на сумму гармонических компонент. В силу сказанного можно предположить, что более близкой математической моделью для пульсаций АД является случайный точечный процесс [15]. Точечный процесс представляет собой возрастающую последовательность моментов времени (точек) наступления некоторых однородных событий, например, прихода пульсовых волн, со случайной длительностью интервалов времени между ними. Отвлекаясь от вопросов изменчивости формы пульсовых волн и рассматривая их последовательность как поток однородных событий, было бы разумно в задачах, связанных с сердечным ритмом, использовать методы какой-либо теории имеющей дело с такими процессами.
Одной из таких хорошо разработанных на сегодняшний день теорий является теория статистической радиолокации (Radar signal processing). Среди главных задач этой теории находится задача определения случайного времени прихода излученного радаром и отраженного от какой-либо цели электромагнитного импульса. Среди наиболее эффективных методов решения этой задачи следует отметить метод согласованной фильтрации (matched filtering) [16]. В этом методе импульсный отклик фильтра так согласуется с импульса радара, чтобы максимум сигнала на выходе фильтра достигался в момент времени прихода отраженного импульса. По существу, согласованный фильтр формирует ковариационную функцию отправленного и принятого импульсов, а хорошо известно, что если оба импульса имеют одинаковую, с точностью до постоянного множителя форму, то максимум ковариации будет достигаться при их совмещении. Соответствующее совмещению смещение между импульсами и будет оценкой времени прихода.
Принцип согласованной фильтрации можно интерпретировать несколько иным, более подходящим для наших задач образом. Именно, если предположить, что в какой-то момент времени t, каким-то образом стало известно время T между импульсами пульсовой волны АД, то зная форму текущего импульса и предполагая, что форма следующего будет почти такой же, можно было бы легко сформировать прогноз будущего сигнала. Для этого следовало бы взять имеющийся фрагмент сигнала длительности T, непосредственно предшествующий текущему моменту времени t и сместить его на время T в будущее. Из теории согласованной фильтрации следует, что ожидаемый импульс АД будет наилучшим образом совмещен с прогнозом. Эта идея проиллюстрирована на Рис.9(B), где также приведено сравнение согласованного прогноза сигнала с прогнозом при ПИД-регулировании. Заметим, что, как это разъяснялось выше, ПИД-регулятор строит прогноз на основе текущих локальных оценок основной частоты f0, амплитуды основного колебания и амплитуд соседних гармоник.
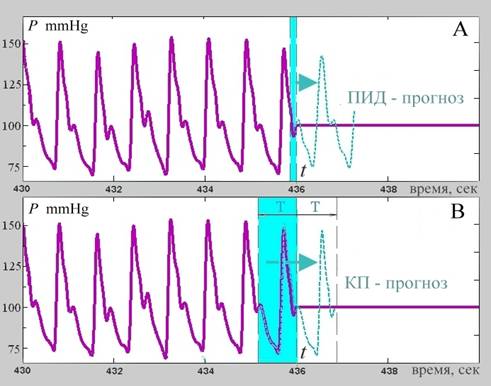
Рис.9. Способы прогнозирования импульсного сигнала, лежащие в основе A – ПИД-регулирования и B – на основе оценки локального квазипериода (КП) T.
Обобщая приведенное выше и проиллюстрированное Рис.9(B) рассуждения, можно констатировать, что при компенсационном измерении АД наиболее эффективным прогнозом ожидаемого импульса будет тот, который является паттерном пульсовой волны. Такой паттерн должен существенно меняться как при изменениях состояний самого объекта, так и при изменении условий его, объекта (активного) измерения. По этой причине реализуемые классическими регуляторами, включая ПИД-регуляторы, паттерны в виде мало-параметрических моделей волны АД малопригодны для активных измерений. Намек на то, как формировать адекватные задаче паттерны содержится в приведенных выше качественных рассуждениях и опирается на свойство квазипериодичности сигнала АД. Это свойство заключается в том, что высокая вариабельность периода сердечных сокращений проявляется только на больших временных интервалах, а на малых, в несколько секунд или несколько сердечных ударов, его изменения обычно малы и лежат в пределах пары процентов. Поэтому, если по мере измерения сигнала АД также формировать оценку его текущего локального периода или, короче, квазипериода (КП) T , то в качестве паттерна можно использовать непосредственно предшествующую моменту времени t предысторию сигнала в точности равную длительности T. Тем самым задача построения паттерна для текущего импульса сигнала сводится к задаче эффективного оценивания его текущего КП.
Задача оценивания изменяющегося КП сердечного
ритма хорошо известна в случае сигналов ЭКГ, где в качестве КП обычно
рассматривается измеренное по R-пикам время между соседними импульсами (RR-интервалы)
и для их нахождения разработаны хорошего качества алгоритмы [17]. Таким образом,
если пульсовая волна АД измеряется одновременно с ЭКГ, то, определяя по ЭКГ текущие
RR-интервалы и принимая их сглаженную версию в качестве
оценки КП, можно описанным выше способом формировать паттерны прогнозируемого
поведения АД. На основе паттернов, в свою очередь, сформируется управление величиной
компенсирующего давления P. Пример подобного управления представлен на Рис.10.
На рисунке показана реальная запись пульсовой волны (АBP signal)
из файла set-p/120.dat базы данных challenge/2014 [18], являющейся составной
частью обширного банка медико–биологического данных PhysioBank. Помимо
сигнала пульсовой волны в файле содержится запись одновременно снятой ЭКГ. По сигналу
ЭКГ найдены положения всех R-пиков, соответствующие данные размещены в
сопровождающем файле аннотаций set-p/120.atr и представлены на Рис.10(А) вместе с гладко
интерполирующей их кривой. С помощью интерполированных RR-интервалов
сигнал АД обрабатывался следующим образом: в каждый из последовательных,
выбранных с шагом 0.1 сек, моментов времени в качестве компенсирующего
давления выбирался фрагмент сигнала давления находящийся по отношению к
текущему моменту времени в прошлом, на величину текущего RR-интервала
(паттерн пульсовой волны). Сравнение формы исходного сигнала АД (АBP signal) и полученного описанным способом компенсирующего
сигнала (shift compensation) приведено на Рис.10 (B).
Из рисунка Рис.10 (B) видно, что компенсирующее давление хорошо повторяет сам сигнал, практически до деталей совмещаясь с последним, за исключением небольшого сбоя на интервале 432-434 сек, обусловленного неизвестной аномалией. На Рис.10 (С) представлен график разности этих двух сигналов (interpolated RR compensation error), он располагается на фоне разности сигнала АД и его же версии, сдвинутой на величину среднего RR (mean RR compensation error). Из Рис.10 (С) видно, что при “мягкой” компенсации с помощью меняющихся RR-интервалов удается избежать связанных с неизбежной вариабельностью локального периода резких выбросов некомпенсированного давления.
В целом Рис.10 подтверждает обосновываемый нами тезис, что измерение АД методом компенсации пульсового давления может и, как мы считаем, должно основываться на управление компенсацией с помощью паттернов пульсовой волны. Даже при грубой оценке локального квазипериода с помощью среднего за интервал ~ 10 сек значения RR-интервала (mean RR compensation), или при чуть более точной оценке – с помощью линейно-слаженной динамики RR-интервалов (interpolated RR compensation) удается достичь лучшей компенсации, чем в случае ПИД-регулирования. Очевидно, что если формировать оценки квазипериода по ЭКГ более аккуратно, например, в соответствии с предложенным в [19] методом, то можно достичь еще большей точности измерений. Однако, движение в этом направлении уводит от основной концепции прибора – управлять активными измерениями АД по самому сигналу пульсового давления, не используя при этом никаких избыточных средств и каналов измерений. Апелляция в приведенном выше обсуждении к сигналу ЭКГ была использована с единственной целью – наглядно продемонстрировать принцип управления компенсацией с помощью паттернов пульсовой волны и обосновать его практические преимущества. Главной же задачей интеллектуализации обсуждаемого активного датчика является разработка и реализация методов и алгоритмов обработки, с помощью которых возможно было бы формировать в реальном времени достаточно точные оценки текущего квазипериода сердечных сокращений по самому регистрируемому сигналу АД.
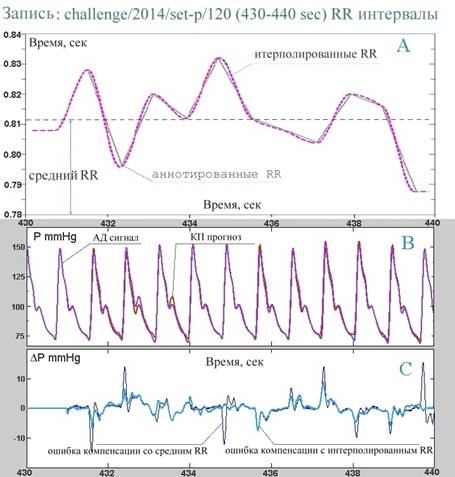
Рис.10. Компенсирующее давление для сигнала АД, построенное с помощью RR-интервалов, выделенных из
сопровождающей АД ЭКГ записи:
A - динамика RR-интервалов и ее гладкая
интерполяция,
B - сравнение сигнала АД и компенсирующего
его сигнала,
С - разность сигнала АД и компенсирующего сигнала на фоне разности
сигнала АД и сдвинутой на величину среднего RR его же версии.
Решение этой проблемы было найдено на основе разработанной авторами концепции многомасштабного корреляционного анализа (МКА) [3,4] и техники аналитических спектров (АСП) [5,6]. Краткое изложение полученных результатов было представлено на конференции OGRW-2014 [21] и в сжатом виде опубликовано в [22]. Ниже, в следующем разделе, мы приводим эти результаты. Нам представляется, что в контексте настоящей работы они будут иметь более адекватное звучание и содержание.
МКА оценивание текущего периода сердечных сокращений по регистрируемому активным датчиком сигналу АД
Основным инструментом многомасштабного корреляционного анализа (МКА) [3,4] является симметричный квадратичный функционал оценки автокорреляционной функции (АКФ) Ra( τ | t ) сигнала АД:
|
(4) |
где p(t’) – сигнал, t – текущее время (момент формирования оценки квазипериода), τ – смещение, играющее роль варьируемого масштаба МКА [4]. Отметим, что в определении оценки Ra(τ | t) (4) время t указано явно, поскольку сигнал АД представляет собой нестационарный процесс. Как хорошо известно, для таких сигналов принципиальной особенностью является зависимость их оценки АКФ от времени. Пример многомасштабной оценки АКФ (4) для реального сигнала АД показан на Рис.11. Изображенная на Рис.11 (A) пульсовая волна представляет собой фрагмент записи сигнала АД из mimic2db/a40008 базы данных MIMIC II Waveform DB [22].
Рис.11(B) ясно показывает, что оценка АКФ (далее просто АКФ) (4) имеет хорошо выраженные боковые пики, соответствующие текущим (для момента времени t) временным характеристикам ритма (положение первого пика соответствует локальному периоду ритма, второго – удвоенному периоду, и т.д.) [4]. Поэтому, значения масштабов τ, задающих положения этих пиков, могут быть использованы в качестве оценок локального периода ритма T (вместо менее устойчивых максимумов самого сигнала!). Преимуществом структуры предложенной нами АКФ (4) является то, что она может быть сформирована на относительно небольшом отрезке сигнала, равным, например, удвоенному максимальному квазипериоду Tmax (который можно, соответственно, взять равным, например, 1,5 сек). Заметим, что традиционные, классические оценки АКФ требуют существенно более длинных отрезков анализа, обычно в ~10 раз длиннее [23].
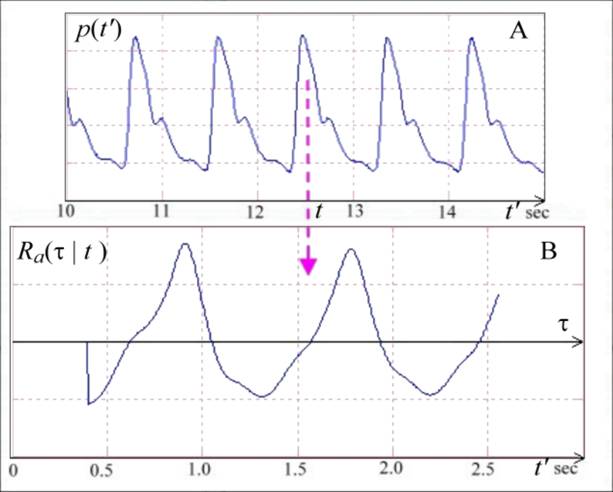
Рис.11. Отрезок реальной записи АД сигнала (A) и оценка его АКФ (B) для заданного момента времени t, выделенного курсором в виде стрелки.
Таким образом, для того, чтобы сформировать оценку локального периода, необходимо надежно определить положение боковых пиков АКФ (4). Опыт исследований показал, что прямое обнаружение пиков с помощью нахождения максимумов исходной АКФ не является достаточно устойчивой процедурой, потому что реальные АКФ имеют, как правило, несигнальные максимумы, обусловленные сопровождающими помехами. Гораздо более стабильной и надежной является процедура нахождения максимумов обобщенного спектра АКФ (Рис.12). Обобщенный спектр Ga( τ | t, σ ) представляет собой обобщенное разложение АКФ Ra( τ’| t ) по семейству оконных функций W( τ’| τ, σ ), имеющих форму вейвлета Морле (5) [24]. Отметим, однако, что в отличие от классического вейвлетного анализа мы считаем спектральной переменной позиции окна τ, а не ширину окна анализа σ, которая предполагается заданной:
|
(5) |
Примеры АКФ Ra( τ’| t ) (4) на фоне спектральных компонент семейства окон W( τ’| τ, σ ) и соответствующий обобщенный спектр Ga( τ | t, σ ) (5) представлены на Рис.12 (А) и (B), соответственно.
Применяя дважды теорему свертки для преобразования Фурье, легко, в приближении τ > σ, получить другое представление обобщенного спектра (5):
|
(6) |
где символ Re означает действительную часть комплексного интеграла и
|
(7) |
представляют собой аналитические спектры (АС) будущего ( Ft ) и прошлого ( Pt ), введенные и подробно обсуждавшиеся в [5].
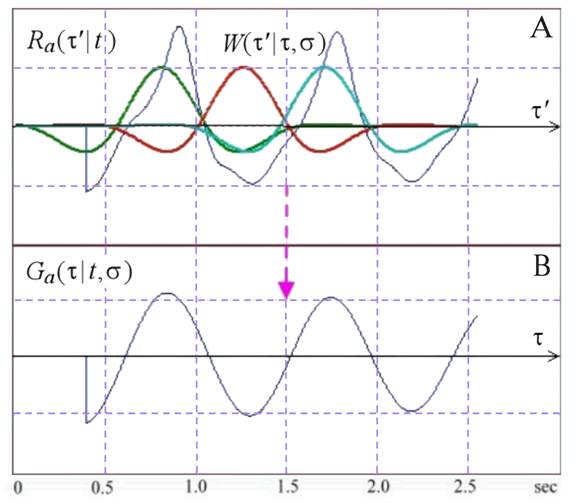
Рис.12. Оценка АКФ Ra( τ’| t ) (Рис.11) с набором спектральных окон W( τ’| τ, σ ) (A) и результирующий обобщенный спектр Ga( τ | t, σ ) (B).
Алгоритм вычисления синтезированного функционала (6) не вызывает особых проблем. Его структура непосредственно видна из (6) и (7): из (6) следует, что численно обобщенный спектр равен нормированному на τ дискретному обратному преобразованию Фурье от взвешенного с гауссовым окном произведения аналитических спектров γFt( f ) и γPt( f ), которые, в силу (7) сами являются результатом преобразований Фурье локального будущего p(t+t’) и локального прошлого p(t–t’) сигнала. Используя для преобразований Фурье быстрые алгоритмы (БПФ), получим быстрый алгоритм и для всей процедуры (6). Кроме того, еще раз напомним, что оценка ритма на основе обобщенного спектра (6) получается надежной, и с высокой точностью оценивает локальный период ритма даже в условиях значительных помех.
Заключение
Изложенные в работе теоретические положения в отношении новых методов мониторинга АД с помощью активных датчиков и управления ими c помощью паттернов пульсовой волны показали высокий потенциал в многочисленных проведенных нами экспериментах по тестированию и совершенствованию разработанного прибора. Это позволяет авторам выразить надежду на хорошие перспективы дальнейшего развития предложенных методов вплоть до внедрения их в ближайшем будущем в практику разработки медицинских приборов.
Работа выполнена при финансовой поддержке гранта РФФИ N 14-07-00496 -а.
Литература
1. Wiener N. Cybernetics: or Control and Communication in the Animal and the Machine. // 2d ed. Cambridge, Mass.: M.I.T. Press., 1962.
2. Chaudhari M., Dharavath S. Study of Smart Sensors and their Applications. // International Journal of Advanced Research in Computer and Communication Engineering, vol. 3, N 1, Jan. 2014.
3. Antsiperov V.E., Obukhov Y.V. Multiscale correlation analysis of real medical and biological signals and their graphical-based representation. // Proceedings of VIII International scientific conference "Physics and radioelectronics in medicine and ecology FRЕME’2008", Vladimir-Suzdal, vol.1, 2008, cc. 180-184.
4. Antsiperov V.E. Multiscale correlation analysis of nonstationary signals containing quasi-periodic fragments. //Journal of Communications Technology and Electronics Vol. 53, № 1, 2008, cc. 65-77.
5. Antsiperov V.E. The concepts of analytic local past / future signal spectra and their use for constructing and analysis of the bilinear time-frequency representations. // Proceedings of the 16-th international conference “Digital signal processing and its applications, DSPA-2014”, Moscow, vol.1, 2014, cc. 113-117.
6. Antsiperov V.Е., Nikitov S.A. Heart rate monitoring based on analytical spectra technique. // Proceeding of Russian-German (until 2012 – Russian-Bavarian) conference on biomedical engineering, St.Petersburg, 2014, cc. 169-171.
7. Marey E.-J. Pression et vitesse du sang. //Physiologie Experimentale, Masson, Paris, 1876.
8. Riva-Rocci S. Un nuovo sfigmomanometro. // Aiuto alla Clin. Med. Prop. - Doc. di Patologia Medica nella R. Univ. di Torino., Torino, 1896.
9. Chung E. et al. Non-invasive continuous blood pressure monitoring: a review of current applications. //Front Med, vol.7 N.1, 2013, cc. 91-101.
10. Peňáz J. Photoelectric measurement of blood pressure, volume and flow in the finger. //Digest of the 10th International Conference on Medical and Biological Engineering, Dresden, 1973, c. 104.
11. K.J. Astrom and T.Hagglund. PID Controllers: Theory, Design and Tuning. Research. 2nd Edition. //Triangle Park, North Carolina: Instrument Society of America, 1995.
12. Klonowski W. From conformons to human brains: an informal overview of nonlinear dynamics and its applications in biomedicine. // Nonlinear Biomedical Physics, vol.1, N.5, doi:10.1186/1753-4631-1-5, 2007.
13. Box G., Jenkins G. Time series analysis: forecasting and control. // Oakland, California: Holden-Day, 1976.
14. Harald M. Stauss. Heart Rate Variability. // Am J Physiol Regul Integr Comp Physiol vol. 285, N.5, 2003, pp 927–931.
15. Daley D.J, Vere-Jones D. An Introduction to the Theory of Point Processes. // Springer, New York, 1988.
16. North, D. O., An Analysis of the Factors Which Determine Signal/Noise Discrimination in Pulsed Carrier Systems. // Reprinted: Proc. IEEE, vol. 51, no. 7, Jul. 1963.
17. Pan J., Tompkins W.J. A Real-Time QRS Detection Algorithm. // IEEE Transactions on Biomedical Engineering , vol. BME-32, no.3, pp.230-236, 1985.
18. Robust Detection of Heart Beats in Multimodal Data // PhysioNet / Computing in Cardiology Challenge 2014, https://physionet.org/challenge/2014/, retrieved 2015-10-14.
19. Antsiperov V.Е., Nikitov S.A. Heart rate monitoring based on analytical spectra technique // Proceeding of X Russian-German (until 2012 – Russian-Bavarian) conference on biomedical engineering, S.Petersburg , 2014, pp. 169-171.
20. V.Е. Antsiperov, K.G. Mansurov, V.V. Bonch-Bruevich. Blood pressure rhythm estimation based on shape patterns for analytic spectra. // Contributions of 9-th Open German-RussianWorkshop on Pattern Recognition and Image Understanding OGRW-2014, Dec. 1–5 2014, Universitat Koblenz-Landau, Koblenz, Germany, 2014.
21. V. E. Antsiperov, K. G. Mansurov, V. V. Bonch-Bruevich. Blood Pressure Rhythm Estimation Based on Shape Patterns for Analytic Spectra. // Proceedings of the 9th Open German-Russian Workshop on Pattern Recognition and Image Understanding, OGRW2014, Active Vision Group (AGAS), Koblenz, Germany, December 1-5, 2015, pp. 47-50.
22. Goldberger AL, Amaral LAN, et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. // Circulation 101(23):e215-e220, 13 June 2000. [Circulation Electronic Pages; http://circ.ahajournals.org/cgi/content/ full/101/23/e215], retrieved 2015-10-14.
23. Otnes R.K. and Enochson L. Applied Time Series Analysis, Volume I: Basic Techniques. // Wiley-Interscience , N.Y., 1978.
24. Mallat S.G. A theory of multiresolution signal decomposition: The wavelet representation. // IEEE Pattern Analysis and Machine Intelligence, vol.11, N.7, 1989, pp. 674–693.