 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 10, 2002 |
 |
ДИНАМИЧЕСКАЯ МОДЕЛЬ РЭЛЕЕВСКОГО КАНАЛА
С ЗАМИРАНИЯМИ
И. М. Орощук
Тихоокеанский военно-морской институт, факультет радиосвязи
Получена 10 октября 2002 г.
В статье представлена динамическая модель рэлеевского канала с замираниями, оценивающая вероятность и число элементарных ошибок в различные моменты времени сеанса связи. Данная модель позволяет точнее оценивать и строить оптимальные алгоритмы повышения помехоустойчивости радиоканалов, и, особенно, для систем, использующих кратковременные сеансы связи.
Особенности распространения радиоволн в силу ряда дестабилизирующих факторов вызывают изменение уровня сигнала в точке приема. Данный эффект вызван многолучевым распространением радиоволн, а также изменением поглощающих свойств среды [1]. Согласно известным моделям, помехоустойчивость такого канала оценивается вероятностью ошибки приема элемента сигнала [2].
При влиянии только гауссовского шума помехоустойчивость когерентного приема двоичных сигналов определяется выражением [2]
, (1)
где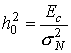 
– энергия сигнала; 
– спектральная плотность помехи; 
– коэффициент корреляции
между используемыми для передачи сигналами; 
–табулированная функция интеграла
вероятностей;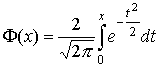 
.
При некогерентном приеме вероятность ошибки оценивается 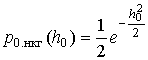[2]:
. (2)
В каналах с глубокими замираниями уровень сигнала, определяемый коэффициентом передачи эфира, распределен по рэлеевскому закону [2]:
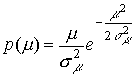, (3)
где m – коэффициент передачи эфира;
– среднеквадратичное
отклонение коэффициента передачи эфира.
Используя
принятые обозначения, для дальнейших преобразований в формулах (1) и (2) произведем
замену переменной 
на
m:
,
,
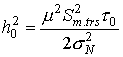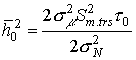где 
– уровень сигнала, излучаемого
передатчиком; 
–
длительность информационной посылки сигнала.
Откуда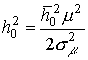 
, а сами выражения вероятностей
ошибки примут вид:
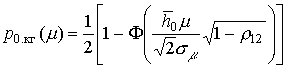, (4)
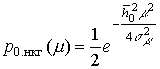. (5)
В реальных условиях происходит группирование ошибок, которое связано с некоторой цикличностью изменений параметров среды, в результате которых уровень сигнала то ослабляется, то наоборот усиливается (рис. 1) [1, 3]. Период данных изменений носит стохастический характер, в результате чего длительности замирания и усиления сигнала также распределены по определенному случайному закону. В зависимости от среды распространения стохастические характеристики замираний носят различный характер. Наиболее глубоким и интенсивным замираниям подвержены каналы, использующие ионосферные или тропосферные радиотрассы, а каналы спутниковой связи, РРЛ и другие наземные системы связи, использующие ультракоротковолновые волны, подвержены менее глубоким и интенсивным замираниям. В этой связи соответствующие каналы будут иметь различные характеристики случайных процессов замираний и, в частности, могут иметь различные законы распределения.
В теории электросвязи явление группирования ошибок известно достаточно давно, и, соответственно, существуют различные модели их описания, которые в той или иной мере адекватно отражают процесс замираний для конкретных типов каналов [3]. Такие модели, чаще всего, основаны на аппроксимации эмпирических данных для конкретных радиолиний, и требуют привязки к некоторым субъективным параметрам (например, к защитному интервалу без ошибок), и, кроме того, не обладают универсальностью использования для различных типов каналов, работающих при разных скоростях манипуляции. Все эти недостатки моделей затрудняют разработку оптимальных способов повышения помехоустойчивости каналов связи.
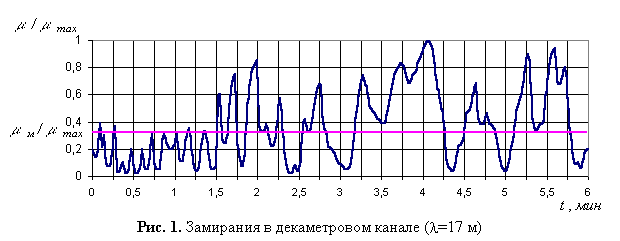
Предлагаемая модель
основана на учете влияния гауссовских шумов и динамических изменений уровня
сигнала. Для оценки динамики замираний в модели процесс изменений уровня
сигнала разделен относительно медианного значения 
на два состояния, в результате чего можно
выделит моменты замирания и усиления сигнала (рис. 2). В момент замираний
уровень сигнала ниже среднего, а в момент усиления выше него. Оба состояния
канала составляют полную группу событий: 
. В результате, с учетом равновероятности состояний,
их величины будут равны 
.
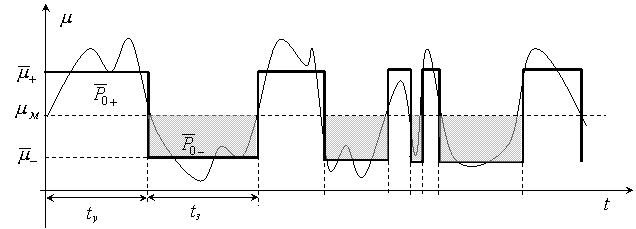
Рис. 2. Пояснение к динамической модели замираний
Для упрощения модели, с некоторым приближением, на интервале замирания и усиления предлагается использовать средние значения коэффициента передачи эфира (см. рис. 2), величины которых для адекватности получим из известных значений числовых характеристик рэлеевского распределения:
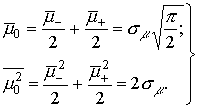
Из
решения системы этих уравнений получим значения средних уровней на интервалах замирания
– 
и усиления
– 
:
,
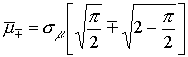из которого
, 
На основании
полученных значений коэффициентов передачи определим вероятности ошибки приема
бита (элемента) информации (
– на участке замирания сигнала, 
– на участке усиления
сигнала), значения которых на соответствующих интервалах уровней для
когерентного приема определяются:
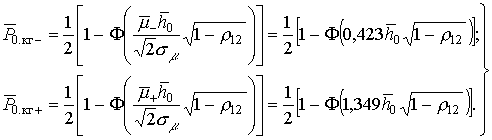(6)
В случае использования некогерентного приема:
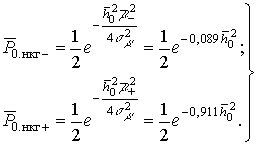(7)
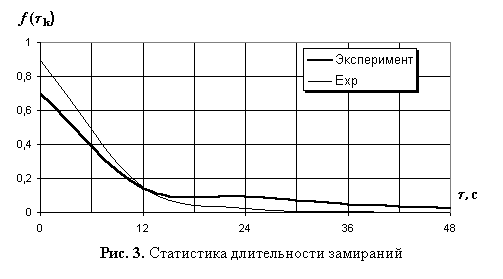
Анализ статистики замираний (см. рис. 1) показал, что длительности замирания и усиления распределены по экспоненциальному закону (рис. 3):
, (8)
где
, 
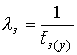– средняя длительность
замирания или усиления сигнала.
В общем случае сеанс
связи может начаться в любой момент времени 
(рис. 4), и в случае попадания в
определенное состояние длительность нахождения в нем r
носит вероятностный характер с плотностью распределения [4]:
,
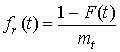где
–
математическое ожидание времени замирания (усиления) сигнала;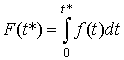 
; f(t) – плотность распределения интервала замирания (усиления).
Рис. 4. Пояснение к определению длительности замирания (усиления) в канале
В случае экспоненциального распределения интервала замирания (усиления):
, 
,
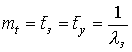откуда
.
Заменив в последнем выражении переменную t* на t , получим
. (9)
Следовательно, плотность распределения нахождения на интервале замирания (усиления) при экспоненциальном распределении совпадает с плотностью распределения длительности самих интервалов.
Для оценки
помехоустойчивости цифровых каналов связи представляет интерес распределение
вероятностей в дискретные интервалы времени, значения которых в дискретные
интервалы времени 
при
определяются
выражением 
(рис.
5).
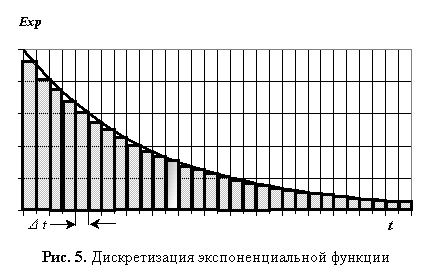
Откуда для случая экспоненциального распределения f(t):
, (10)
где
t0 – длительность элементарной посылки сигнала; n – количество элементарных посылок, укладывающих на
интервале времени 
.
В этом случае среднее число элементов, укладываемых в средний интервал замирания (усиления), определяется математическим ожиданием:
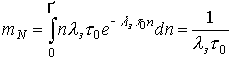. (11)
В данном случае полная вероятность приема m – элементов с ошибкой в одном из состояний канала будет определяться байесовским выражением
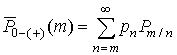, (12)
где 
– вероятность того, что
длительность состояния замирания (усиления) будет равна 
[определяется по формуле (10)]; 
– условная вероятность
ошибочного приема m элементов, в случае замирания на интервале ; 
; 
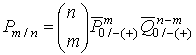– условная вероятность ошибки одной
элементарной посылки сигнала при попадании в состояние замирания (усиления)
сигнала [определяется по формулам (6) для когерентного приема и (7) – для
некогерентного приема]; 
.
Для упрощения
выражения (12) воспользуемся асимптотикой Пуассона при 
, 
[5]:
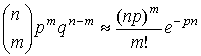. (13)
Откуда
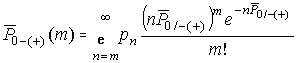. (14)
В результате, с учетом экспоненциального распределения pn, согласно формуле (10), выражение (14) примет вид
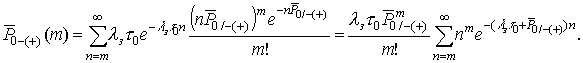
Пользуясь формулой суммирования Эйлера-Маклорена [6], с небольшой погрешностью, можно воспользоваться приближением:
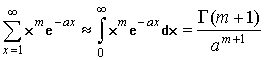. (15)
В результате, последнее выражение можно упростить:
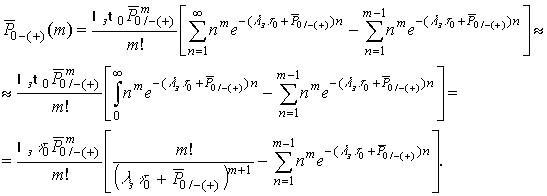(16)
Следует
заметить, что в выражении (16) при 
и 
величина второго слагаемого на порядок и
более меньше первого, в связи с чем с заданной погрешностью им можно
пренебречь. В результате, окончательное приближенное выражение оценки
вероятности m
ошибок на интервале замирания (усиления) примет вид (рис. 6):
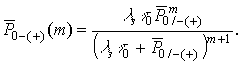(17)
 |
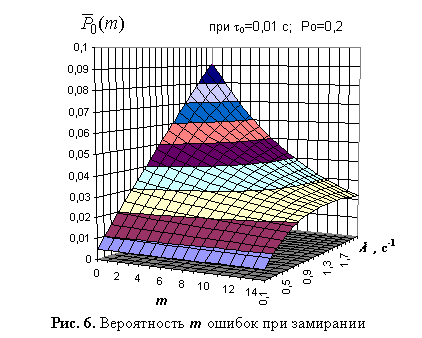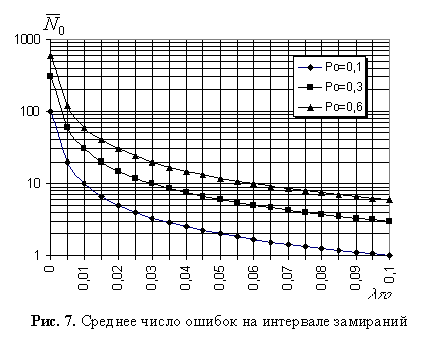
Анализ выражения (17) показывает, что для фиксированной длительности элементарной посылки (скорости манипуляции в канале) и энергетических параметрах сигнала при снижении интенсивности замираний зависимость вероятности числа ошибок приближается к равномерному распределению, в противном случае оно переходит в явно экспоненциальное распределение с большой крутизной спада (см. рис. 6), что, соответственно, изменяет число группируемых ошибок.
Для разработки помехоустойчивых систем связи представляет интерес статистика распределения ошибок в процессе передачи сообщений, для чего определим среднее число ошибок в одном из состояний. Среднее число ошибок с учетом усреднения на всех интервалах замирания (усиления) определяется выражением
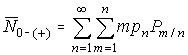. (18)
Для упрощения выражения
(18) при воспользуемся
приближением аналогичным вышерассмотренному [см. формулу (13)], исходя из чего
получим:
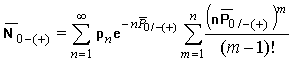. (19)
Далее
с учетом сходимости суммы [6]: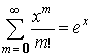 
, получим приближенное выражение
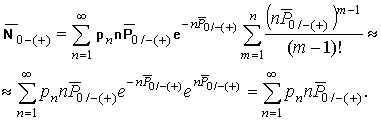(20)
Подставив в формулу (20) выражение (10), получим
.
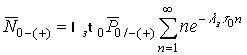С учетом что 
,
с определенной погрешностью воспользуемся приближением [см. формулу (15)], в
результате чего:
,
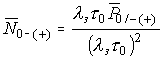откуда, окончательно, среднее число ошибок на интервале замирания (усиления) будет определяться приближенным выражением
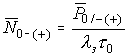. (21)
На рис. 7 представлена зависимость среднего числа ошибок на интервале замирания (усиления).
 |
Из выражения (21) с учетом формулы (11) определим плотность числа ошибок на интервале замирания (усиления):
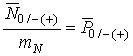, (22)
величина которой практически определяется битовой вероятностью ошибки.
Таким образом, разработанная модель, учитывающая статистику амплитудных и временных параметров радиотрассы, дает возможность с помощью оценок средней вероятности ошибок, средней плотности и среднего числа ошибок точнее определить реальную исправляющую способность используемых избыточных кодов канала связи в критических условиях замирания, и, соответственно, вести разработки более эффективных способов повышения помехоустойчивости. Наибольшая целесообразность применения данной модели характерна для систем связи, использующих кратковременные сеансы связи, так как именно для них применение классических моделей помехоустойчивости [2, 5] дают наибольшую погрешность расчета.
Литература
1. Долуханов М. П. Флуктуационные процессы при распространении радиоволн. М.: Связь, 1971. – 184 с.
2. Зюко А. Г. Помехоустойчивость и эффективность систем связи. М.: Связь, 1972. – 360 с.
3. Головин О. В. Декаметровая радиосвязь. М.: Радио и связь, 1990. – 240 с.
4. Вентцель Е. С., Овчаров Л. А. Теория случайных процессов и ее инженерные приложения. М.: Наука, 1991. – 384 с.
5. Левин Б. Р. Теоретические основы статистической радиотехники. – 3-е изд. – М.: Радио и связь, 1989. – 656 с.
6. Справочник по специальным функциям с формулами, графиками и таблицами: Под ред. М. Абрамовица, И. Стиган, Пер. с англ. / Под ред. В. А. Диткина, Л. Н. Кармазиной. М.: Наука, 1979.– 832 с.
Орощук Игорь Михайлович – к.т.н., доцент, докторант кафедры радиосвязи Тихоокеанского военно-морского института, E-mail: Oroshchuk@yandex.ru
 |
 |