|
|
"JOURNAL OF RADIOELECTRONICS" N 10, 2003 |
|
A Noise Reduction Algorithm Suitable for Hardware Implementation
Vladimir Radenkovic1, Miodrag Temerinac2, Nikola Teslic1, MiroslavPopovic1
1 - University of Novi Sad, Faculty of Engeenering, Fruskogorska 11a, 21000 Novi Sad, Serbia & Montenegro, e-mail: vradenkovic@tvns.co.yu
2 – Micronas GmbH, Hans Bunte Str. 9, Freiburg, Germany
Received October 29, 2003
In recent years there have been a lot of research and development activities, in both industry and academia, in area of image processing and in noise reduction in particular. However, there is a need for more research efforts in this area because most of the proposed algorithms are to complex for the implementation on embedded platforms, which typically have very limited resources. This paper should be viewed as a contribution to these efforts. In the paper we propose new algorithm and its hardware implementation for the impulse noise reduction filter for the satellite TV picture. This space 2D filter processes the picture in real-time. Its structure is based on median filter and it operates by replacing the noise damaged pixels with values calculated by median filter 3x3. To determine whether a pixel is a noise damaged or not, morphological functions are applied, and because of this the filter was named NMF (New Morphological Filter). The filter equally well reduces the real impulse noise present in a satellite TV picture, in real-time, as it does the salt and paper type of impulse noise. The algorithm hardware implementation was done in FPGA (Field Programming Gate Array) integrated circuit. The NMF’s quality is low mathematical complexity, small demand for hardware resources, a large signal to noise ratio, as well as fine preservation of both edges and tiny details in the filtered picture.
Keywords: Morphological filter, Noise reduction, Satellite TV, Hardware implementation, FPGA, Salt and paper, Image processing, Mathematical complexity
1. INTRODUCTION
One of the most interesting peculiarities of real-time picture processing is the fact that the noise reduction filter quality is not measured only by the filtration success in terms of the filtered picture quality, but also by the demand for hardware resources necessary for its implementation. The demand for the hardware resources could be characterized by the size of the integrated circuit (e.g. number of gates needed, capacity of the memory, etc.), and its working frequency, i.e. clock rate.
If the proposed filter is to be used in commercial SAT TV sets, this means the production cost of such a filter should be relatively low. The production cost is in relation to the number of logical circuits needed for implementation of the algorithm. For this reason it is necessary that the algorithm should be as simple as possible, i.e. its complexity should be as low as possible.
Operational speed is an essential characteristic. It depends on the mathematical complexity of the algorithm. Additionally, the operational speed of the integrated circuit could be reduced by the decomposition of the algorithm into a set of hardware blocks which operate in parallel. On the other hand, if the algorithm could not be decomposed in such a way, this would lead to a structure with a series of hardware blocks, where each of the blocks must wait for a result (output) of the previous block (its input) in order to perform the processing, and to finally produce its own result. It is clear that serial connection of hardware blocks increases the overall delay and thus implies higher operation speed, i.e. working frequency.
Exploiting of memory resources is another significant characteristic, so for these reasons the proposed filter is designed as a space two dimensions (2D) filter, which processes each half-picture in order to avoid additional memories for storing half-pictures.
Our goal was to implement a filter algorithm in the FPGA ALTERA 10K 100, i.e. the algorithm that respects the actual limits of hardware resources available in this FPGA [1]. The problem in finding such an algorithm is that the unique criterion for the filter quality estimation does not exist in the literature. One of the commonly accepted objective criterions is SNR. Other criterions are subjective, and they address the preservation of edges, contours, and fine details, the corresponding marks are “good” and “bad”. J.Pitas and A.Venestanopoulus [2] propose the following five criterions for the filter quality estimation:
- preservation of fine details,
- preservation of edges,
- bias,
- SNR, and
- mathematical complexity
Pitas and Venetsanopoulos [2] have compared the nonlinear image processing algorithms known from the literature. The result of this comparison for the algorithms that are most relevant to the problem at hand is given in the Table 1.
Table 1: The result of the comparison of the relevant algorithms from the literature
|
Filter |
Comparison Criterions |
||||
|
A |
B |
C |
D |
E |
|
|
Median |
0 |
2 |
2 |
2 |
1 |
|
Separate Median |
0 |
2 |
2 |
2 |
2 |
|
Recursive Median |
0 |
2 |
2 |
2 |
1 |
|
Dilation |
0 |
2 |
0 |
0 |
2 |
|
Erosion |
0 |
2 |
0 |
0 |
2 |
|
Open |
0 |
2 |
2 |
0 |
1 |
|
Close |
0 |
2 |
2 |
0 |
1 |
|
C/O |
0 |
2 |
2 |
1 |
0 |
|
O/C |
0 |
2 |
2 |
1 |
0 |
The comparison criterions in the Table 1 are as follows:
A: preservation of fine details
B: preservation of edges
C: bias
D: salt and paper noise reduction efficiency
E: mathematical complexity
The marks for the criterions in Table 1 are defined in the Table 2:
Table 2: The definition of marks for the criterions given in Table 1.
|
A, B, D |
0: bad |
1: average |
2: good |
|
C |
0: strong |
1: average |
2: weak |
|
E |
0: large |
1: average |
2: small |
Table 2 shows that bad preservation of fine details is the greatest disadvantage of median-based filters including Median [2],[3],[4],[5],[6],[7],[8],[9],[10], Separate Median [11], and Recursive Median [12]. On the other hand, increased noise reduction efficiency and decreasing of bias by the Morphological filters [13],[14],[15],[16] is paid with the increased mathematical complexity, yielding higher demand for hardware resources.
The NMF filter proposed in this paper was designed by combining the principles of morphological and median filters in order to achieve high level of noise reduction, measured by SNR, and at the same time good preservation of fine details by using median approximation of neighboring pixels. In essence, the NMF filter algorithm is based on the application of mathematical morphology [17].
For the evaluation of the quality of the proposed filter, in terms of noise reduction, we use the signal/noise ratio (SNR), which is the usual objective measure in such a case.
In the paper we compare the NMF with three similar filters known from the literature [18-20]. Filters will be compared according to their mathematical complexity measured by the number of needed operations, efficiency of the noise reduction measured by the SNR, and the quality of preservation of edges and fine details in the picture measured by subjective impression of differences between the pictures produced by various algorithms and the original picture with presence of noise.
The special advantage of the proposed NMF algorithm, in comparison with the three algorithms from the literature [18-20], is that it is more successful in noise reduction of the real noise present in the real satellite TV picture. The real noise signal manifests in a form of bright and dark dashes a few pixels long in contrast to the theoretical paper and salt noise that affects only individual pixels.
Filter efficiency was evaluated subjectively since in realty there is no original noiseless sequence. The results have been confirmed by a theoretic salt-and-pepper type noise model upon which measuring of the signal/noise ratio have been carried out.
2. Concept of the NMF Filter
The requirements that impose themselves in the construction of this filter should reconcile two opposite points of view; on the one side maximal efficiency in noise reduction, and on the other side minimum edge and fine details degradation on the other. The problem faced in this complex optimization task is that both noise and fine details happen to be high-frequency components of a satellite TV signal, so by suppressing the noise, fine details are being suppressed, as well. The solution lies in construction of a filter that will filter only the spots in the picture that noise damaged.
If there is a possibility to detect impulse noise damaged picture parts, they could be selectively filtered. This means that only those pixels which are damaged by the noise get replaced by new values calculated by a median filter. The essence of the proposed concept is in an adequate detection of noise damaged picture parts.
Selective filtering of only damaged elements of a picture results in the restored picture that will have a lot more of preserved details. The improvements result in increase of the signal/noise ratio and in meeting of the subjective criteria.
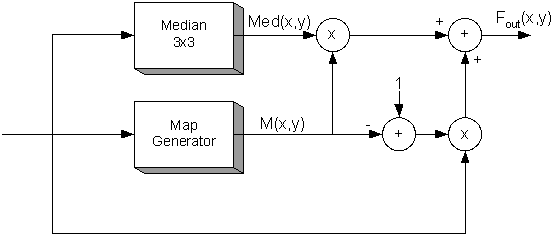
The Figure 1 presents the flow chart of the filtering process. Filtered picture Fout(x,y) is obtained from the input noise damaged picture Fin(x,y) and the picture Med(x,y) that is obtained by filtering the picture Fin(x,y) through a median filter. Pixels in the output picture Fout(x,y) represent a linear combination of the noise damaged picture and the same picture filtered by a median filter.
Figure 1. Flow chart of the filtering process.
The values of the functions Med(x,y), Fin(x,y), and Fout(x,y) represent of brightness in a point (x, y). The function M(x,y), that is called the “noise map”, serves to detect the noise damaged pixels. Its value is 1 in places where pixels are damaged, and 0 in all other cases.
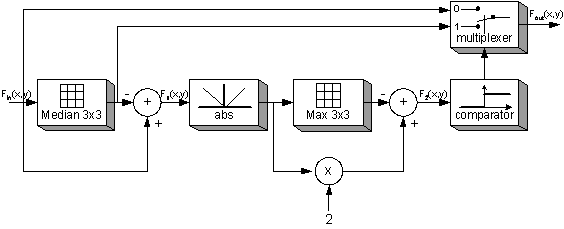
The filtering procedure is represented by a functional block diagram shown in Figure 2 and consists of 2 steps.
I STEP
In the first step, the function F1(x,y) is being
calculated. It determines the
possible candidates for noise-damaged pixels. Each pixel for witch the
luminance component value, Fin(x,y), is different from the median
filtered luminance component value, Med(Fin(x,y)), is a possible
candidate. The absolute value of this difference is defined as follows:
where ABS is the represents the absolute value. The absolute value is introduced of the difference is introduced so that the function F1(x,y) has non negative values.
II STEP
In second step we calculate the values of the function F2(x,y). The function F2(x,y) is used to specify the criterion for defining the candidates that could be declared as noise-damaged pixels. Pixels damaged by the noise have very high luminance component values, maximum value or values close to maximum. If we define window of size m by n pixels, e.g. 3x3, on top of the picture, the pixels with the luminance component values close to maximum, or maximum, represent the pixels damaged by the noise. The filtering process proceeds from the top to the bottom of the picture by sliding the observed window by one pixel in each step. If we define the observed pixel as a pixel in the center of the observed window, (xc,yc), the value of the difference between the F1(x,y) function maximum for the window, MAX(F1(x,y)) and F1(x,y) function value for the observed pixel, F1(xc,yc), has to be smaller than the difference between F1(xc,yc) and the F1(x,y) function minimum for the window, MIN(F1(x,y)):
After simple transformation we obtain the following condition:
MAX(F1(x,y)) and MIN(F1(x,y)) represent the extrems in the observed window. By experiments we have find out that the following relaxed condition may be used in the NMF heuristic filtration algorithm:
Let functions MAX(F1(x,y)) and MIN(F1(x,y)) be morphological functions Dilation and Erosion [17], DIL(F1(x,y)) and ER(F1(x,y)). Than condition (4) becomes the following:
Next, in the process of filtration the noise map M(x,y) is defined as:
The output picture Fout(x,y) is defined as follows:
Figure 2. Filter NMF Block Scheme
3. short description of algorithms used as references
The most appropriate filters that have been described in the literature, which function in a similar way as the NMF are used for the comparison with the NMF. The following filters have been selected:
MK algorithm [18] observes the difference between the Med(Fin(xc,yc)) and Fin(xc,yc), and if this difference is between the two thresholds, T1 and T2, it is assumed that the pixel has not been damaged by the noise. The thresholds T1 and T2 are defined as follows:
Sl and Sh are Fin(x,y) function minimum and maximum for the observed window, respectively, while Smin and Smax are the lowest and the highest possible values of function Fin(x,y), i.e. 0 and 255.
SAM algorithm [19] differs from MK [18] in the definition of thresholds. Thresholds, T1 nad T2, are defined as follows:
where c=1/2, 2/3, 3/4…. , Smax=255, Smin=0, and m=Med(Fin(xc,yc))
ROM algorithm [20] sorts values of Fin(x,y) for the pixel in the observed window (e.g. 3x3) by the increasing order. The pixel in the center of the window is skipped. Let rk(n) represent the k-th element of sorted array of pixels in n-th position of the observed window. Next, the value m(n) is defined as follows:
Let x(n) represent the central point of the observed window in it’s n-th position in the current picture. Than the distances dk of individual elements, of sorted array of pixels, from this central point, x(n), are defined as follows:
If the distance dk is greater than Tm, dk>Tm, the corresponding pixel is damaged, and it’s brightness value is replaced by the value m(n). The values of Tm are defined as follows:
T1=8, T2=20, T3=40, and T4=50.
In the following sections of the paper we present the results of the comparison of NMF algorithm with the three algorithms from the literature [18-20].
4. results
Mathematical complexity
The total number of mathematical operations that is used by the filtering algorithm determines its mathematical complexity [2]. The mathematical operations are divided into the following groups:
A= Series Sorting
B= Adding and deducting
C= Dividing and mulitiplying
D= Comparing
E= Logical I
F= If-else
G= Absolute value
The comparative results are presented in Table 3. It is obvious that the NMF is superior to the three algorithms from the literature since it requires only 8 operations. The most close to it is SAM, with 9 operations, MK requires a little bite more, 11 operations, and the worst one is ROM with its 27 operations.
Table 3: Mathematical complexity of the observed filters
|
|
A |
B |
C |
D |
E |
F |
G |
TOTAL |
|
MK |
3 |
2 |
2 |
2 |
1 |
1 |
0 |
11 |
|
SAM |
1 |
2 |
2 |
2 |
1 |
1 |
0 |
9 |
|
ROM |
1 |
9 |
1 |
12 |
0 |
4 |
0 |
27 |
|
NMF |
2 |
2 |
1 |
1 |
0 |
1 |
1 |
8 |
Noise reduction
Since we had only a sequence of pictures received from the satellite TV receiver at our disposal, i.e. the original sequence of pictures sent from the TV studio was unavailable; the SNR could not be calculated. In such situation the filtering results could be evaluated only subjectively regarding the success of the real noise reduction. In our experiments we used a zoomed detail, see Fig. 4, from the TV satellite picture shown in Fig. 3.

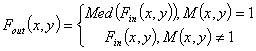









 , (14)
, (14)










