УДК 551.594:004.021:004.045:004.67:004.622

Обратная задача радиочастотного зондирования ионосферы

А. Ю. Гришенцев¹, А. Г. Коробейников²

¹-Санкт-Петербургский государственный университет информационных технологий, механики и оптики

²-Институт земного магнетизма, ионосферы и распространения радиоволн им. Н. В. Пушкова Российской Академии наук (ИЗМИРАН), Санкт-Петербургское отделение

 

Получена 29 октября 2010 г.

 

Аннотация. Разработана модель решения обратной задачи вертикального зондирования ионосферы применительно к данным, полученным на ионосферных станциях типа «АИС-М».  На основе разработанной модели реализовано программное приложение для автоматизированной обработки и анализа спектрограмм высотного зондирования ионосферы. Апробация программного продукта позволила выявить достаточно высокую эффективность предложенного метода, что позволяет позиционировать разработанную модель как эффективный способ решения обратной задачи высотного зондирования ионосферы.

Ключевые слова: ионосфера, вертикальное зондирование, спектрограмма, обратная задача, высотное распределение электронной плотности.

 

Введение

Исследование ионосферы является актуальной задачей для многих областей человеческой деятельности. Особенный интерес у исследователей вызывает изучение распространения электромагнитных волны в замагниченной плазме ионосферы [1], как с точки зрения самих исследований процесса, так и с точки зрения применения в практической радиосвязи. Сущность обратной задачи радиочастотного зондирования состоит в нахождении ряда физических характеристик среды путем исследования влияния слоистой ионосферы на радиосигналы. Одной из ключевых характеристик ионосферы является высотное распределение электронной плотности. Наличие станций иносферного зондирования по всему миру и их плотное сотрудничество через мировые центры данных, позволяет получать информацию о глобальном распределении электронной плотности в ионосфере Земли. Наряду с методами радиочастотного зондирования в современных исследованиях активно применяется метод радиопросвечивания ионосферы [2]. Особенно актуальным (с точки зрения глобальных, регулярных наблюдений) метод радиопросвечивания стал после вывода на орбиты высокоорбитальных спутников GPS и ГЛОНАСС и низкоорбитальных GRACE, COSMIC, LEO и ряда других, с помощью которых на сегодня осуществляется более 5600 сеансов затменных измерений каждые сутки, в более чем 2000 районах. Совокупность всех исследований позволяет получить практически в режиме реального времени данные о глобальном состоянии ионосферы Земли. Одной из проблем современных исследований при прогнозировании состояния ионосферы является недостаточность статистических наблюдений, что обусловлено относительной молодостью рассматриваемых методов. Таким образом, актуальной является задача рассмотрения архивных данных ионосферных исследований и их дополнительный анализ, позволяющий увеличить объемы статистической информации. В статье рассмотрена проблема моделирования высотного распределения электронной плотности на основании данных радиозондирования ионосферной станцией «АИС-М».

 

Постановка целей и задач

В рамках работы необходимо выполнить анализ спектрограмм высотного зондирования ионосферы (СВЗИ), моделирование высотного распределения электронной плотности на основании данных радиозондирования ионосферной станцией «АИС-М».

Задачами работы является:

– разработка методов анализа СВЗИ;

– разработка обобщённой математической модели для решения обратной задачи с учётом особенностей СВЗИ;

– реализация разработанной математической модели в виде программы.

 

Анализ особенностей спектрограмм полученных методом вертикального радиозондирования

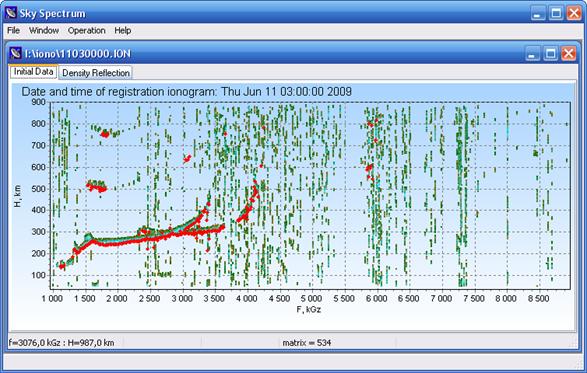
Спектрограммы вертикального радиозондирования получаются в результате приёма отражённого от ионосферы сигнала в диапазоне от 1 МГц до 20 МГц, с минимальным шагом по частоте 1 кГц. Диапазон зондируемых высот составляет от 50 км до 1500 км, частота повторения импульсов 40 Гц. Мощность передатчика не менее 2.5 кВт. Полученные данные оцифровываются и сохраняются в сжатом виде.

Одной из сложностей, с которыми приходится сталкиваться при анализе ионограмм – зашумлённость, вызванная локальными неоднородностями ионосферы, а в последнее время лавинообразным ростом антропогенного заполнения радиочастотных диапазонов. Особенно заметным стало влияние радиошумов на СВЗИ с распространением цифровых каналов передачи информации использующих сложные виды модуляции с большим числом низших гармоник. Таким образом, первой задачей для анализа СВЗИ является выделение высотных следов отражения. Решение данной задачи выполнялось с применением комплексных статистических методов обработки информации. Для предварительной локализации областей, в которых наиболее вероятно присутствие первых отражений (по простой траектории отражения в соответствии [3] слои D, E, F1) рассчитывалась высотная плотность распределения отражённых сигналов:

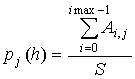,                                               (1)

где: – амплитуда отражённого сигнала, из матрицы СВЗИ  с координатами ; – координата по горизонтали (соответствует частоте), – координата по вертикали (соответствует высоте ), – число ненулевых элементов по горизонтали (т.е. из множества ), причем для исключения деления на ноль полагаем, что: . Здесь необходимо отметить, что весь предварительный анализ производился в действующих высотах, это связано с тем, что расчёт реальной высоты становится возможным только после определения высотного распределения электронной плотности в ионосфере. Выражение (1) хорошо локализует области с горизонтальным или близким к горизонтальному расположением отражённого следа, т.е. области, где величина  мала (– частота, – высота следа). Локализация областей с достаточно высокими значениями , обычно соответствующим критическим частотам слоя, где групповая скорость волны ,  по оценке величины затруднительна. Введение величины горизонтальной плотности распределения позволяет решить задачу локализации следа отражений только на СВЗИ с относительно малым уровнем шума, что не представляет особенного интереса. Дальнейшая локализация отражённых следов в СВЗИ производилась с учётом значений , следующим образом (алгоритм 1):

– (a) осуществлялся проход по вертикальной координате матрицы;

– (b) при встрече ненулевого линейного элемента  () определялось наличие ненулевых значений в матрице в элементах с координатами , где – являются допусками по горизонтали и вертикали соответственно, значение  задаётся в виде константы, а  – рассчитывается как функция ;

– (с) если условие (b) выполнялось заданное число  раз для элемента , то линейный элемент , считался следом отражения в СВЗИ.

В результате анализа СВЗИ по алгоритму 1 получается матрица , в которой ненулевые значения соответствуют различным компонентам отражений электромагнитной волны от ионосферы (рис.1).  Часть (b) указанного алгоритма была реализовано в виде рекуррентной функции, что позволило учитывать особенности смещения следа отражения по высоте при движении по частоте, т.е. производить предварительную аппроксимацию паттерна следа отражения. Аппроксимация позволяет сделать частичное, предварительное выделение различных следов отражения. В общем виде решить задачу разделения на составляющие o-обыкновенной, x-необыкновенной и z-компоненты (магнитоионная компонента) на этом этапе анализа не представляется возможным.

 

 

Рис. 1. Программная реализация фильтрация СВЗИ по алгоритму 1. Серым цветом обозначена исходная СВЗИ, чёрным – фильтрация (ненулевые элементы матрицы ).

 

В наиболее зашумлённых СВЗИ перед выполнением указанного алгоритма производилась предварительная фильтрация путём выделения областей с высокими значениями энтропии. Оценку энтропии можно произвести следующим образом (алгоритм 2):

– матрица СВЗИ разбивается на несколько равных друг другу прямоугольных областей  (для выравнивания ряд вертикальных векторов матрицы соответствующих самым высоким частотам и несколько горизонтальных векторов соответствующих наибольшим значениям высоты можно не рассматривать);

– каждая прямоугольная область  разбивается на равные прямоугольники , для которых рассчитывается суммарная амплитуда:  , далее рассчитываются векторы плотности распределения для всех областей , причём каждый элемент отдельного вектора плотности распределения для области  рассчитывается для ;

– для каждой области  рассчитывается значение энтропии:

 ,                                        (2)

где – вектор плотности распределения амплитуд для области .

На основании полученных значений энтропий для различных областей СВЗИ производится фильтрация путём отсеивания областей с наиболее высокими значениями энтропии. Рассмотренный метод фильтрации на основании оценки энтропии в связи с возможностью потери большого числа значимых данных применялся только в тех случаях, когда рассмотренные ранее методы локализации отражённых следов в СВЗИ не дают удовлетворительных результатов.

 Использование фильтрации необходимо для начального определения локализации следов отражения в СВЗИ, конечное построение следов отражения наиболее целесообразно производить по исходной матрице СВЗИ , по алгоритму 1, с учётом зашумлённости СВЗИ путем корректирования значений коэффициентов .

 

Определение высотных характеристик ионосферы по данным предварительного анализа СВИЗ

Наиболее интересными областями СВЗИ являются те участки, в которых 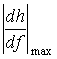, причём области в которых:

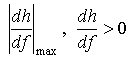                                                 (3)

 

будут соответствовать критическим частотам слоя, для – обыкновенной, –необыкновенной и – z-компоненты электромагнитной волны (рис.2). С учётом локализации области отражения и построения матрицы , нахождение производной , не представляет сложностей. Кроме критических частот по условию:

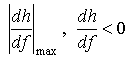                                                 (4)

можно определить – гирочастоту слоя, которая, вообще говоря, может быть определена для конкретного географического места исходя из значения в [Гс] у поверхности Земли [3]:

,                                                     (5)

где: – высота над поверхностью земли [км], – радиус Земли в данном месте [км],  –гирочастота в [МГц]. Магнитную индукцию при ионосферных исследованиях принято выражать в Гауссах, перевод в систему Си (Тесла) может быть осуществлён с помощью следующего соотношения:

.                                        (6)

 

Исходя из практического постоянства  для данного места (5), можно осуществить проверку полученных данных применения выражение, связывающее критические частоты обыкновенной и необыкновенной волны с гирочастотой [3]:

.                                                (7)

 

 

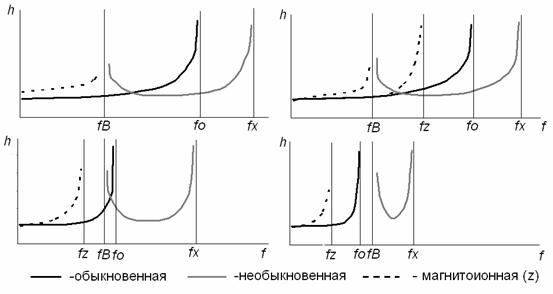
Рис. 2. Некоторые характерные виды СВИЗ, при различных соотношениях частот:

b.) ; c.) ; d.) .

 

На основании полученных значений критических частот и следов отражения СВЗИ в виде матрицы  вычисляется высотное распределение электронной плотности :

,                              (8)

где – плазменная частота электронов [МГц], для максимумов электронной плотности  будет соответствовать критической частоте . По полученным точкам для высотного распределения электронной плотности с помощью стандартных методов аппроксимации можно получить гладкую кривую  [5].

Следующей задачей является расчёт фактической высоты с учётом высотного распределения электронной плотности . Решить эту задачу можно по групповому времени распространения электромагнитной волны, с учётом прямого и обратного движения [4]:

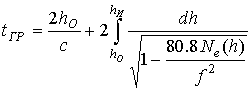,                                 (9)

где: – высота расположения ионосферы над поверхностью Земли в данном месте (определяется по высоте отражения низших частот из матрицы ), – высота ионосферы для которой рассчитывается , – частота зондирующей электромагнитной волны, – скорость света в вакууме.

 

Обсуждение

В ходе исследований произведён анализ СВЗИ, с точки зрения особенностей шумовых составляющих, разработана математическая модель фильтрации СВЗИ. Полученные в результате фильтрации исходных СВЗИ данные позволяют производить расчёт высотной характеристики .

Анализ данных ионосферной станции Воейково (Санкт-Петербург) за (2002, 2003 гг.) показал, что разработанные методы фильтрации позволяют определить значение критической частоты  в 68 % случаев, 23 % СВЗИ были отсеяны на уровне фильтрации как неподдающиеся машинному анализу из-за высокого уровня шумов, в 9% СВЗИ критические частоты, были определены с точностью менее 16%.

Решение проблемы возникающих при анализе СВЗИ ошибок и неопределённостей в силу высокого уровня шума возможно с помощью взаимодействия мировой сети ионосферных станций, глобального радиозатменного мониторинга ионосферы и атмосферы Земли. Перспективным направлением зондирования ионосферы являются современные методы частотно-углового зондирования, позволяющие на стадии аппаратного анализа производить разложение отражённого сигнала на составляющие его компоненты, например как это реализовано в Digisonde™ Portable Sounder (DPS) [6].

 

Литература

1.     Гинзбург В.Л., Рухадзе А.А. Волны в магнитоактивной плазме. Издание второе, переработанное. Главная редакция физико-математической литературы из-ва «Наука», 1975. – 256 с.: ил.

2.     Яковлев О. И., Павельев А. Г., Матюгов С. С. Спутниковый мониторинг Земли: Радиозатменный мониторинг атмосферы и ионосферы. – М.: Книжный дом «Либроком», 2010. – 208 с.

3.     Piggott W.R., K. Rawer. URSI handbook of Ionogram Interpritation and Reduction. INAG (Ionospheric Network Advisory Group) WORLD DATA CENTER A. National Academy of Sciences, 2101 Constitution Avenue, N.W. Washington, D.C., U.S.A., 20418/Second edition, november, 1972. –145 p.

4.     Яковлев О. И., Якубов В. П., Урядов В. П., Павельев А. Г. Распространение радиоволн. – М.: ЛЕНАНД, 2009. – 496 с.

5.     Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Из-во «Наука», 1970. – 664 с.

6.     Background to Ionospheric Sounding. [Electronic resource]: — Access mode: http://ulcar.uml.edu/DPS.htm, 01854 — Title of screen. — open. 600 Suffolk Street, 3rd floor Lowell, MA, Lang. English.