УДК 535.42, 535.13
АНАЛИЗ РАССЕЯНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН СИСТЕМОЙ НАНОРАЗМЕРНЫХ ЧАСТИЦ В ТОНКОЙ МЕТАЛЛИЧЕСКОЙ ПЛЕНКЕ МЕТОДОМ ДИСКРЕТНЫХ ИСТОЧНИКОВ
А.В. Барышев
физический факультет МГУ имени М.В. Ломоносова, кафедра
математики
Получена 20 октября 2010 г.
Аннотация. На основе метода дискретных источников реализована математическая модель оптической антенны. Проведен анализ рассеяния плоской электромагнитной волны антенной, представляющей собой совокупность нескольких наноразмерных частиц сфероидальной формы, расположенных в тонкой металлической пленке, которая нанесена на стеклянную подложку. Приведены результаты компьютерного моделирования рассеянной , в том числе в области неизлучающих волн.
Ключевые слова: оптическая антенна, метод дискретных источников, наноразмерные частицы.
Введение
В последнее время внимание ученых все больше привлекает такая область науки как плазмоника. В частности большое внимание уделяется вопросу изучения рассеивающих свойств оптических антенн [1-3], зачастую представляющих собой кластер наноразмерных частиц, расположенных на подложке или в тонких металлических пленках, которые в свою очередь наносятся на поверхность подложки. Подобно антеннам радио- и микроволнового диапазона, оптические антенны преобразуют энергию свободно распространяющего излучения в энергию локализованной волны, и наоборот. Оптические антенны позволяют усилить взаимодействие света с веществом, что дает возможность с успехом использовать их для повышения эффективности работы таких устройств, как биосенсоры, солнечные батареи, переключатели излучения, светоизлучающие органические диоды и другие [2].
В последнее время особое внимание было уделено исследованию характеристик рассеяния оптической антенны типа Яги [4-6], представляющей собой пять наноразмерных частиц (активный вибратор, рефлектор, и три директора) из благородного металла. Частицы располагались в свободном пространстве или в слоистой среде без поглощения, где индексы рефракции всех слоев приблизительно одинаковы, что позволяет рассматривать подобную среду как однородное пространство. В работах [4,5] было показано, что при возбуждении подобной системы в свободном пространстве квантовой точкой, расположенной вблизи активного вибратора, антенна рассеивает излучение в определенном направлении. Подобные результаты также были получены в работе [6], когда антенна располагалась в слоистой среде без поглощения с приблизительно одинаковыми индексами рефракции, и возбуждалась плоской электромагнитной волной, распространяющейся перпендикулярно оси антенны.
Чуть более десяти лет назад было открыто явление аномального просачивания энергии через наноразмерные отверстия в экране, сделанном из благородного металла [7]. Тремя годами позднее появилась работа [8], в которой было дано объяснение этому явлению, связанному с возбуждением плазмонов [9]. На основе математического моделирования было обнаружено экстремальное просачивание энергии через металлическую пленку, нанесенную на стеклянную призму, в которой присутствовало наноразмерное отверстие [10] или неоднородность [11], причем эффект проявляется в резком (на порядок) возрастании амплитуды интенсивности рассеяния исключительно в области неизлучающих волн, за углом полного внутреннего отражения.
В данной работе на основе метода дискретных источников проводится анализ рассеивающих свойств оптической антенны в области неизлучающих волн. Антенна представляет собой совокупность наноразмерных частиц, имеющих те же характеристические размеры, что и частицы, рассмотренные в работе [6]. Но в отличие от приведенной работы, мы рассматриваем кремниевые частицы, расположенные в тонкой пленке из благородного металла, которая нанесена на поверхность стеклянной призмы. В качестве внешнего возбуждения рассматривается неизлучающая плоская электромагнитная волна, распространяющаяся под таким углом, что это приводит к эффекту экстремального просачивания энергии.
Математическое моделирование оптических свойств подобных антенн с использованием таких методов, как метод конечных элементов [12], или метод конечных разностей во временной области [13], может быть неточным в силу того, что этим методы не позволяют строго учесть взаимодействие между частицами и бесконечной границей раздела подложка-пленка-воздух. Метод дискретных источников лишен подобного недостатка и позволяет строго учесть все возможные взаимодействия. В числе прочего, МДИ позволяет одновременно решать задачу для нескольких углов падения, а также для обеих поляризаций P/S плоской волны.
Математическая постановка задачи рассеяния
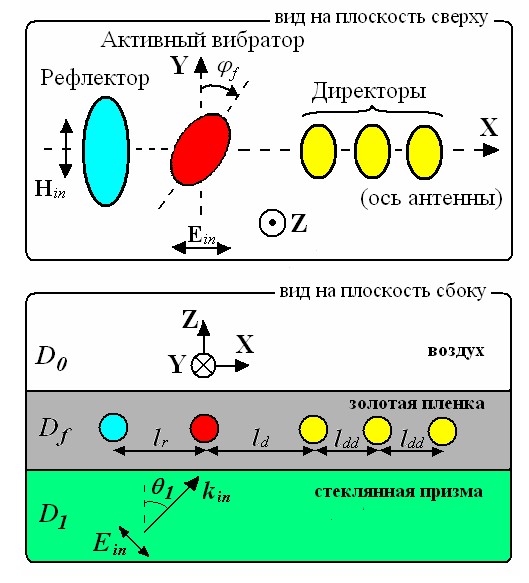
Математическую постановку будем проводить для ![]() частиц произвольной формы, расположенных в среде с плоско-параллельными слоями
(рис. 1). Введем прямоугольную систему координат с началом на плоскости
раздела подложка- металлическая пленка так, что эти плоско-параллельные слои
делят все пространство
частиц произвольной формы, расположенных в среде с плоско-параллельными слоями
(рис. 1). Введем прямоугольную систему координат с началом на плоскости
раздела подложка- металлическая пленка так, что эти плоско-параллельные слои
делят все пространство
![]() на три области:
на три области: ![]()
![]() , которую занимает стеклянная подложка,
, которую занимает стеклянная подложка, ![]()
![]() ,
которую занимает металлическая пленка толщины
,
которую занимает металлическая пленка толщины ![]() , и
, и ![]()
![]() ,
которую занимает воздух. Плоскость раздела подложка- металлическая пленка
обозначим через
,
которую занимает воздух. Плоскость раздела подложка- металлическая пленка
обозначим через ![]()
![]() . Плоскость раздела металлическая пленка-
воздух обозначим через
. Плоскость раздела металлическая пленка-
воздух обозначим через ![]()
![]() . Таким образом ось
. Таким образом ось ![]() направлена перпендикулярно плоскостям
направлена перпендикулярно плоскостям ![]() и
и ![]() в
сторону области
в
сторону области ![]() ,
которую занимает воздух. Проводящая пленка занимает пространство между
плоскостями
,
которую занимает воздух. Проводящая пленка занимает пространство между
плоскостями ![]() и
и ![]() .
. ![]() частиц с гладкой границей произвольной
формы, внутреннюю область которых обозначим
частиц с гладкой границей произвольной
формы, внутреннюю область которых обозначим ![]()
![]() ,
расположены целиком внутри пленки. Полагаем, что области
,
расположены целиком внутри пленки. Полагаем, что области ![]() являются односвязными. Границы частиц
обозначим через
являются односвязными. Границы частиц
обозначим через ![]() . В качестве внешнего
возбуждения будем рассматривать поле линейно поляризованной плоской волны
. В качестве внешнего
возбуждения будем рассматривать поле линейно поляризованной плоской волны ![]() , падающей из стеклянной
подложки
, падающей из стеклянной
подложки ![]() под углом
под углом ![]() относительно нормали на
плоскую границу
относительно нормали на
плоскую границу ![]() подложка-пленка.
Тогда математическая постановка задачи рассеяния будет иметь вид
подложка-пленка.
Тогда математическая постановка задачи рассеяния будет иметь вид
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() (1)
(1)
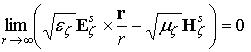 ,
, ![]()
![]()
![]() ,
, ![]()
Здесь ![]() - полные, а
- полные, а ![]() -
рассеянные поля в соответствующих областях
-
рассеянные поля в соответствующих областях ![]() ,
, ![]() - орт
- орт ![]() декартовой системы координат,
декартовой системы координат, ![]() - вектор нормали к поверхностям
- вектор нормали к поверхностям
![]()
![]() . Мы
также полагаем, что параметры сред удовлетворяют условиям
. Мы
также полагаем, что параметры сред удовлетворяют условиям ![]() (временная зависимость выбрана в виде
(временная зависимость выбрана в виде ![]() ). В этом случае
граничная задача имеет единственное решение. Отметим, что в областях
). В этом случае
граничная задача имеет единственное решение. Отметим, что в областях ![]() полное поле включает в себя падающую и
отраженную плоские волны, а в области
полное поле включает в себя падающую и
отраженную плоские волны, а в области ![]() -
преломленную волну.
-
преломленную волну.
Прежде чем строить приближенное решение для рассеянных полей, решим задачу
дифракции плоской волны ![]() на слоистой структуре
воздух-пленка-подложка. Это решение можно записать в явном виде [15]. Полученное
поле обозначим
на слоистой структуре
воздух-пленка-подложка. Это решение можно записать в явном виде [15]. Полученное
поле обозначим ![]()
![]() . Поле
внешнего возбуждения внутри пленки
. Поле
внешнего возбуждения внутри пленки ![]() для
P/S-поляризованного
возбуждения плоской волны может быть записано как
для
P/S-поляризованного
возбуждения плоской волны может быть записано как
![]() ,
, ![]()
где для P-поляризации
![]() ,
, ![]()
и для S-поляризации
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
, ![]()
Здесь ![]() ,
, ![]() -
соответствующие коэффициенты отражения и преломления на плоской границе,
разделяющей
-
соответствующие коэффициенты отражения и преломления на плоской границе,
разделяющей ![]() и
и ![]() [15].
[15].
Теперь будем строить приближенное решение задачи для рассеянного поля ![]() в
в ![]()
![]() и
полного поля в
и
полного поля в ![]() на основе метода дискретны источников
(МДИ) [14].
на основе метода дискретны источников
(МДИ) [14].
Суть МДИ заключается в представлении поля в виде
конечной линейной комбинации полей дискретных источников, которая аналитически
удовлетворяет системе уравнений Максвелла в областях ![]() , условиям на бесконечности для рассеянного
в
, условиям на бесконечности для рассеянного
в ![]() поля, а также условиям сопряжения для
тангенциальных компонент полей на
поля, а также условиям сопряжения для
тангенциальных компонент полей на ![]() . В
результате чего решение граничной задачи рассеяния (1) сводится к аппроксимации
поля внешнего возбуждения на поверхностях частиц
. В
результате чего решение граничной задачи рассеяния (1) сводится к аппроксимации
поля внешнего возбуждения на поверхностях частиц ![]()
![]() полями дискретных источников. Неизвестные
амплитуды ДИ определяются только из условий сопряжения на поверхностях частиц
полями дискретных источников. Неизвестные
амплитуды ДИ определяются только из условий сопряжения на поверхностях частиц ![]() ,
которые принимают вид:
,
которые принимают вид:
Где ![]() ,
, ![]() . Таким образом решение задачи (1),
первоначально сформулированной в неограниченной области, сведено к задаче
аппроксимации полей внешнего возбуждения на поверхностях частиц.
. Таким образом решение задачи (1),
первоначально сформулированной в неограниченной области, сведено к задаче
аппроксимации полей внешнего возбуждения на поверхностях частиц.
Приближенное решение будем строить для частиц произвольной формы. В основу для
представления рассеянного поля положим систему электрических диполей,
удовлетворяющих условиям сопряжения для тангенциальных компонент полей на
плоскостях ![]() , что позволяет учесть аналитически
всевозможные переотражения полей между частицами и плоскостями раздела сред
[16]. Для q-ой частицы
, что позволяет учесть аналитически
всевозможные переотражения полей между частицами и плоскостями раздела сред
[16]. Для q-ой частицы ![]() диполи
локализованы в точках
диполи
локализованы в точках ![]() и
располагаются всюду плотно не некоторой вспомогательной поверхности
и
располагаются всюду плотно не некоторой вспомогательной поверхности ![]() ,
, ![]() ,
которая располагается строго внутри
,
которая располагается строго внутри ![]() .
Структура полей ДИ будет определяться тензором Грина слоистой среды:
.
Структура полей ДИ будет определяться тензором Грина слоистой среды:
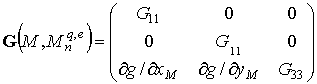
При этом компоненты тензора могут быть записаны в виде интегральных представлений Зоммерфельда
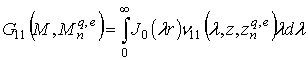
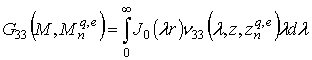
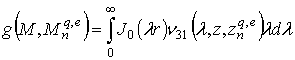
где ![]() ,
, ![]() ,
, ![]() -
цилиндрическая функция Бесселя,
-
цилиндрическая функция Бесселя, ![]() -
координаты точки
-
координаты точки ![]() . Для спектральных
функций
. Для спектральных
функций ![]() ,
, ![]() ,
, ![]() ,
обеспечивающих выполнение условий сопряжения на границах
,
обеспечивающих выполнение условий сопряжения на границах ![]() слоистой среды, справедливы следующие
представления [17]:
слоистой среды, справедливы следующие
представления [17]:
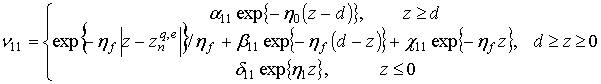
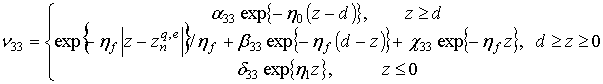
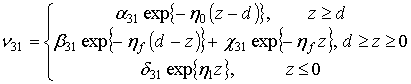
Здесь ![]() . Коэффициенты
. Коэффициенты
![]() ,
, ![]() ,
, ![]() определяются из условий сопряжения,
которым удовлетворяют спектральные функции, на границах
определяются из условий сопряжения,
которым удовлетворяют спектральные функции, на границах ![]() [16]:
[16]:
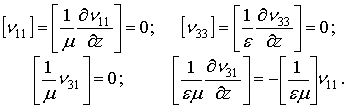
Где ![]() - скачок
переменной при переходе через поверхность.
- скачок
переменной при переходе через поверхность.
Для q-ой частицы ![]() полагаем,
что в каждой точке
полагаем,
что в каждой точке ![]() располагаются три
линейно независимых электрических диполя, ориентированных в соответствии с
цилиндрической системой координат. Тогда векторные потенциалы q-ой частицы, связанные с представлением рассеянного поля
и соответствующие каждому такому источнику, можно представить как:
располагаются три
линейно независимых электрических диполя, ориентированных в соответствии с
цилиндрической системой координат. Тогда векторные потенциалы q-ой частицы, связанные с представлением рассеянного поля
и соответствующие каждому такому источнику, можно представить как:
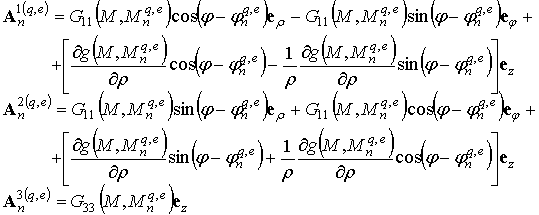
Для q-ой частицы ![]() диполи,
представляющие поле внутри частицы, локализованы в точках
диполи,
представляющие поле внутри частицы, локализованы в точках ![]() и
располагаются всюду плотно не некоторой вспомогательной поверхности
и
располагаются всюду плотно не некоторой вспомогательной поверхности ![]() ,
, ![]() ,
которая располагается строго внутри
,
которая располагается строго внутри ![]() .
Векторные потенциалы q-ой частицы
.
Векторные потенциалы q-ой частицы ![]() ,
связанные с представлением полного поля внутри частицы, могут быть записаны
следующим образом:
,
связанные с представлением полного поля внутри частицы, могут быть записаны
следующим образом:
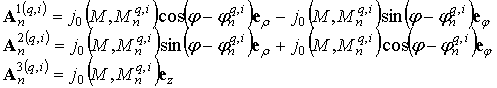
Здесь ![]() , где
, где ![]() - сферическая функция Бесселя нулевого
порядка.
- сферическая функция Бесселя нулевого
порядка.
Тогда для приближенного решения граничной задачи (1) справедливо следующее представление:
Где ![]() и
и
![]() представляют рассеянное системой частиц
поле во внешней области
представляют рассеянное системой частиц
поле во внешней области ![]() , а
, а ![]() и
и ![]() представляют
полное поле внутри
q-ой частицы.
представляют
полное поле внутри
q-ой частицы. ![]() и
и
![]() - количество дискретных источников,
выбираемых на вспомогательных поверхностях
- количество дискретных источников,
выбираемых на вспомогательных поверхностях
![]() и
и ![]() , и
представляющих поле в соответствующих областях.
, и
представляющих поле в соответствующих областях.
Построенное таким образом представление для приближенного решения удовлетворяет
всем условиям граничной задачи (1), за исключением условий сопряжения на
поверхностях частиц. Удовлетворяя условиям (2) в норме ![]() , где
, где
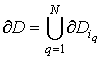 , определим
, определим
![]() . Заметим, что с помощью единого набора
амплитуд мы строим представление для рассеянного поля сразу во всех трех
областях
. Заметим, что с помощью единого набора
амплитуд мы строим представление для рассеянного поля сразу во всех трех
областях ![]() .
.
Имеет место следующее утверждение.
Теорема. Пусть электрические диполи локализованы в
точках ![]()
![]() и располагаются всюду плотно на
вспомогательной нерезонансной для данного волнового числа
и располагаются всюду плотно на
вспомогательной нерезонансной для данного волнового числа ![]() поверхности
поверхности
![]() ,
, ![]() , при
этом поверхность
, при
этом поверхность ![]() располагается строго внутри
располагается строго внутри ![]() . Тогда
приближенное решение вида (3) сходится равномерно к точному решению задачи (1) в
любой конечной области полупространства
. Тогда
приближенное решение вида (3) сходится равномерно к точному решению задачи (1) в
любой конечной области полупространства
![]() .
.
Вычислительный алгоритм МДИ
Следуя обобщенному методу поточечной сшивки, позволяющему получить наиболее
стабильные результаты [18], неизвестные амплитуды дискретных источников будем
определять как решение переопределенной системы линейных уравнений. Суть
обобщенного метода поточечной сшивки заключается в том, что на поверхности
каждой частицы выбирается набор точек коллокаций ![]() , равномерно покрывающих эту поверхность
[18]. Затем, повторяя эту операцию для каждой частицы, а также задавая на
вспомогательных поверхностях внутри частицы набор дискретных источников
, равномерно покрывающих эту поверхность
[18]. Затем, повторяя эту операцию для каждой частицы, а также задавая на
вспомогательных поверхностях внутри частицы набор дискретных источников ![]() и
и ![]() ,
представляющих рассеянное поле вне частицы и полное поле внутри частицы, мы
получим переопределенную систему линейных уравнений размерности
,
представляющих рассеянное поле вне частицы и полное поле внутри частицы, мы
получим переопределенную систему линейных уравнений размерности ![]() . Затем неизвестные амплитуды мы определяем
путем псевдообращения. Отметим, что применение подобной схемы позволяет
одновременно вычислять характеристики рассеяния для обеих поляризаций P- и S-типа и набора углов
падения плоской волны
. Затем неизвестные амплитуды мы определяем
путем псевдообращения. Отметим, что применение подобной схемы позволяет
одновременно вычислять характеристики рассеяния для обеих поляризаций P- и S-типа и набора углов
падения плоской волны ![]() .
.
Во всех наших численных экспериментах мы
рассматривали кластер сферических частиц, обладающий симметрией относительно
плоскости ![]() . При этом дискретные источники
располагались на вспомогательных сферах, радиус которых был вдвое меньше радиуса
рассматриваемых сферических частиц, а координаты и количество источников,
представляющих рассеянное поле вне частиц и полное поле внутри частиц,
совпадали.
. При этом дискретные источники
располагались на вспомогательных сферах, радиус которых был вдвое меньше радиуса
рассматриваемых сферических частиц, а координаты и количество источников,
представляющих рассеянное поле вне частиц и полное поле внутри частиц,
совпадали.
Для вычисления характеристик рассеянного поля на бесконечности необходимо
вычислить диаграмму рассеяния. В области ![]() она
определяется следующим образом:
она
определяется следующим образом:
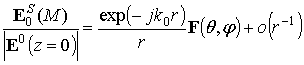 ,
,
![]() ,
, ![]()
Для получения конкретного вида диаграммы рассеяния
для приближенного решения (3) достаточно использовать асимптотические
представления для интегралов Зоммерфельда.
Тогда ![]() - компоненты диаграммы
рассеяния записываются следующим образом:
- компоненты диаграммы
рассеяния записываются следующим образом:
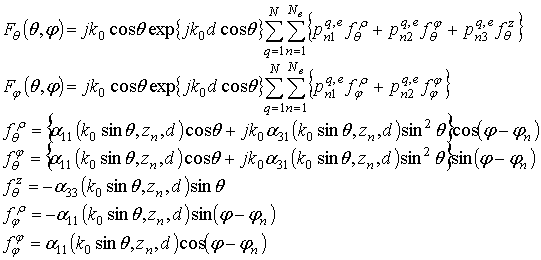
Обсуждение результатов моделирования
Нас интересует интенсивность рассеянного поля в
области ![]() ,
которая имеет вид:
,
которая имеет вид:
![]()
В качестве внешнего возбуждения во всех численных
экспериментах будем рассматривать
P-поляризованную плоскую волну единичной
амплитуды с длиной волны ![]() нм, волновой вектор
которой лежит в плоскости
нм, волновой вектор
которой лежит в плоскости ![]() , распространяющуюся из призмы, сделанной
из стекла BK-7 с индексом рефракции
, распространяющуюся из призмы, сделанной
из стекла BK-7 с индексом рефракции ![]() . P-поляризация
плоской волны была выбрана, поскольку в этом случае наблюдается эффект
экстремального просачивания энергии [11]. Пусть
. P-поляризация
плоской волны была выбрана, поскольку в этом случае наблюдается эффект
экстремального просачивания энергии [11]. Пусть ![]() - преломленный угол, под
которым волна проходит в
- преломленный угол, под
которым волна проходит в ![]() . В этом случае соотношение Снеллиуса имеет
вид
. В этом случае соотношение Снеллиуса имеет
вид ![]() . Поскольку показатель преломления стекла
больше показателя преломления воздуха, то при изменении угла падения
. Поскольку показатель преломления стекла
больше показателя преломления воздуха, то при изменении угла падения ![]() в диапазоне от 0 до
в диапазоне от 0 до ![]() наступает момент, начиная с
которого
наступает момент, начиная с
которого ![]() . Тогда
. Тогда ![]() и
и ![]() . Таким
образом, в верхнем полупространстве возникает неизлучающая волна, которая
распространяется вдоль границы раздела (оси
. Таким
образом, в верхнем полупространстве возникает неизлучающая волна, которая
распространяется вдоль границы раздела (оси ![]() ) и экспоненциально затухает по нормали к
границе (вдоль оси
) и экспоненциально затухает по нормали к
границе (вдоль оси ![]() ). При длине волны
). При длине волны ![]() нм для стекла с индексом рефракции
нм для стекла с индексом рефракции ![]() критический угол
критический угол ![]() , за которым
располагается область неизлучающих волн, оказывается равным
, за которым
располагается область неизлучающих волн, оказывается равным ![]() .
.
Во всех численных экспериментах в качестве
рассеивателей будем рассматривать кремниевые частицы
![]() сфероидальной формы, большая ось которых
параллельна плоскости
сфероидальной формы, большая ось которых
параллельна плоскости ![]() . Диаметр меньшей оси всех сфероидов
одинаков и равен
. Диаметр меньшей оси всех сфероидов
одинаков и равен ![]() нм, показатель
преломления
нм, показатель
преломления ![]() . Частицы целиком расположены внутри
золотой пленки
. Частицы целиком расположены внутри
золотой пленки
![]() толщины
толщины
![]() нм, имеющей показатель преломления
нм, имеющей показатель преломления ![]() , таким образом, что они удалены от
плоскостей
, таким образом, что они удалены от
плоскостей ![]() на одинаковое расстояние. Толщина пленки
выбрана исходя из условия возникновения плазмонного резонанса [11]. Для данной
конфигурации плазмонный резонанс наблюдается при угле падения волны
на одинаковое расстояние. Толщина пленки
выбрана исходя из условия возникновения плазмонного резонанса [11]. Для данной
конфигурации плазмонный резонанс наблюдается при угле падения волны ![]() градусов. Рассеянную
интенсивность мы будем анализировать в плоскости падения плоской волны
градусов. Рассеянную
интенсивность мы будем анализировать в плоскости падения плоской волны
![]() :
: ![]() .
.
Рис.1. Оптическая антенна
Конечной целью исследования является анализ
характеристик рассеяния оптической антенны, состоящей из одного «активного
вибратора», «рефлектора», и трех «директоров», размеры которых сходны с
размерами частиц, рассмотренных в [6]. Центры всех частиц лежат на одной прямой ![]() , называемой осью оптической антенны.
Прямоугольная система координат выбрана таким образом, что ось
, называемой осью оптической антенны.
Прямоугольная система координат выбрана таким образом, что ось ![]() проходит через центр активного
вибратора, а ось оптической антенны параллельна оси
проходит через центр активного
вибратора, а ось оптической антенны параллельна оси ![]() . Причем во всех численных
экспериментах, приведенных ниже, положение центра «вибратора» постоянно, а
изменяется лишь угол
. Причем во всех численных
экспериментах, приведенных ниже, положение центра «вибратора» постоянно, а
изменяется лишь угол ![]() между его большей осью, длина которой 85
нм, и осью
между его большей осью, длина которой 85
нм, и осью
![]() . «Рефлектор» и «директоры» располагается
по разные стороны от «активного вибратора» так, как показано на рис. 1. Причем
во всех численных экспериментах большие оси «рефлектора» и «директоров», длины
которых равны 100 и 60 нм соответственно, перпендикулярны оси антенны.
. «Рефлектор» и «директоры» располагается
по разные стороны от «активного вибратора» так, как показано на рис. 1. Причем
во всех численных экспериментах большие оси «рефлектора» и «директоров», длины
которых равны 100 и 60 нм соответственно, перпендикулярны оси антенны.
Рассмотрение начинаем с анализа характеристик
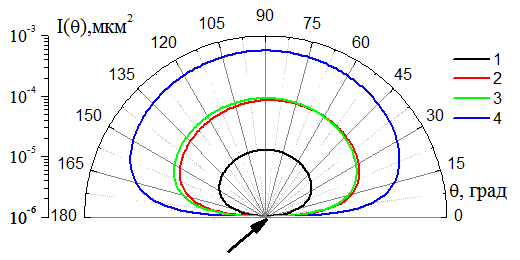
рассеяния «активного вибратора». На рис. 2 приведено сравнение интенсивности
рассеяния в логарифмическом масштабе в плоскости падения волны в зависимости от
положения «активного вибратора» и угла падения плоской волны. Кривая 1
соответствует нормальному падению волны, кривая 2-наклонному падению под углом ![]() в случае, когда большая
ось «активного вибратора» параллельна оси
в случае, когда большая
ось «активного вибратора» параллельна оси ![]()
![]() . Случаю, когда большая ось
параллельна оси оптической антенны
. Случаю, когда большая ось
параллельна оси оптической антенны ![]()
![]() , соответствуют кривые 3 (нормальное
падение) и 4 (падение под углом
, соответствуют кривые 3 (нормальное
падение) и 4 (падение под углом ![]() ). Черная стрелка на
рисунке показывает направление падения волны, в случае если она распространяется
под углом к оси
). Черная стрелка на
рисунке показывает направление падения волны, в случае если она распространяется
под углом к оси ![]() . Как можно видеть, падение волны
под углом
. Как можно видеть, падение волны
под углом ![]() , приводящее к
возникновению плазмонного резонанса, выражается в увеличении интенсивности
рассеяния почти на порядок. При этом также оказывается, что расположение
сфероида вдоль оси
, приводящее к
возникновению плазмонного резонанса, выражается в увеличении интенсивности
рассеяния почти на порядок. При этом также оказывается, что расположение
сфероида вдоль оси ![]()
![]() ,
дает увеличение интенсивности еще почти на один порядок. Поэтому во всех
дальнейших численных экспериментах в качестве внешнего возбуждения мы будем
рассматривать волну, распространяющуюся под углом
,
дает увеличение интенсивности еще почти на один порядок. Поэтому во всех
дальнейших численных экспериментах в качестве внешнего возбуждения мы будем
рассматривать волну, распространяющуюся под углом ![]() .
.
Рис.2. Интенсивность рассеяния на «активном вибраторе» в
зависимости от угла ![]() падения
плоской волны и угла
падения
плоской волны и угла ![]() между большей осью «вибратора» и осью
между большей осью «вибратора» и осью ![]() . 1:
. 1: ![]() , 2:
, 2: ![]() , 3:
, 3: ![]() , 4:
, 4: ![]() .
.
На рис. 3 приводится сравнение интенсивности
рассеяния двумя частицами- «активным вибратором» и «рефлектором»- в зависимости
от угла ![]() между
большей ось «вибратора» и осью
между
большей ось «вибратора» и осью
![]() . Расстояние между центрами частиц
. Расстояние между центрами частиц ![]() нм.
Угол
нм.
Угол ![]() последовательно
принимает следующие значения:
последовательно
принимает следующие значения:
![]() (кривая 1),
(кривая 1), ![]() (кривая 2),
(кривая 2), ![]() (кривая 3),
(кривая 3), ![]() (кривая 4). Из рисунка видно, что поворот
«активного вибратора» приводит не только к увеличению интенсивности рассеяния,
но также и к смене направления рассеяния излучения.
(кривая 4). Из рисунка видно, что поворот
«активного вибратора» приводит не только к увеличению интенсивности рассеяния,
но также и к смене направления рассеяния излучения.
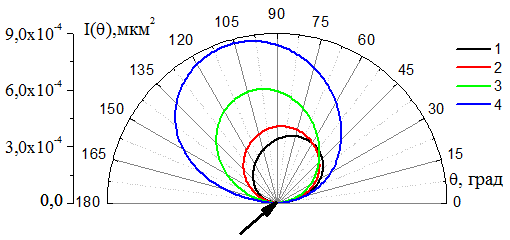
Рис.3. Интенсивность рассеяния на системе «активный вибратор» -
«рефлектор» в
зависимости от угла ![]() между
большей осью
между
большей осью
«вибратора» и осью ![]() .
Расстояние между центрами частиц
.
Расстояние между центрами частиц
![]() нм.
1:
нм.
1: ![]() , 2:
, 2: ![]() ,
3:
,
3: ![]() , 4:
, 4: ![]()
Преследуя цель получить максимально возможную
интенсивность, исходя из рис. 3, «активный вибратор» далее был расположен вдоль
оси антенны ![]() , а «рефлектор» последовательно смещался в
сторону от «вибратора» вдоль оси антенны. Результаты моделирования зависимости
рассеянной интенсивности от расстояния между центрами частиц
, а «рефлектор» последовательно смещался в
сторону от «вибратора» вдоль оси антенны. Результаты моделирования зависимости
рассеянной интенсивности от расстояния между центрами частиц ![]() приведены
на рис. 4 в виде кривых: 1 (
приведены
на рис. 4 в виде кривых: 1 (![]() нм), 2
(
нм), 2
(![]() нм), 3 (
нм), 3 (![]() нм), 4 (
нм), 4 (![]() нм), 5 (
нм), 5 (![]() нм). Из рисунка видно, что увеличение
расстояния между частицами приводит к изменению направления рассеяния излучения.
При этом излучение происходит в направлении падающей волны при больших
расстояниях между частицами, и «в противоположном» при небольших расстояниях.
Стоит также отметить, что при расстояниях между центрами частиц, превышающими
360 нм, начинают появляться заметные побочные лепестки излучения, поэтому
расстояния, большие указанной величины не рассматривались.
нм). Из рисунка видно, что увеличение
расстояния между частицами приводит к изменению направления рассеяния излучения.
При этом излучение происходит в направлении падающей волны при больших
расстояниях между частицами, и «в противоположном» при небольших расстояниях.
Стоит также отметить, что при расстояниях между центрами частиц, превышающими
360 нм, начинают появляться заметные побочные лепестки излучения, поэтому
расстояния, большие указанной величины не рассматривались.
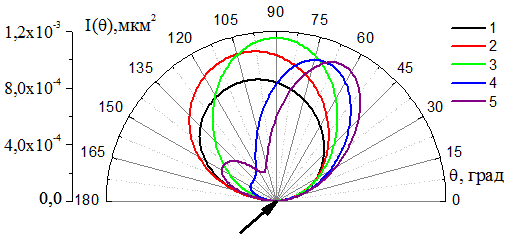
Рис.4. Интенсивность рассеяния на системе «активный вибратор» -
«рефлектор» в зависимости от расстояния между центрами частиц
.
,
. 1:
нм, 2:
нм, 3:
нм,
4:
нм, 5:
нм
На рис. 5 приводится сравнение интенсивности
рассеяния двумя частицами- «активным вибратором» и «директором»- в зависимости
от угла ![]() между
большей ось «вибратора» и осью
между
большей ось «вибратора» и осью ![]() . Расстояние между
центрами частиц
. Расстояние между
центрами частиц ![]() нм.
Угол
нм.
Угол ![]() последовательно
принимает следующие значения:
последовательно
принимает следующие значения:
![]() (кривая 1),
(кривая 1), ![]() (кривая 2),
(кривая 2), ![]() (кривая 3),
(кривая 3), ![]() (кривая 4). Как и в случае рассеяния на
системе «вибратор-рефлектор» видно, что поворот «активного вибратора» приводит к
смене направления рассеяния излучения, но не приводит к увеличению интенсивности
рассеяния.
(кривая 4). Как и в случае рассеяния на
системе «вибратор-рефлектор» видно, что поворот «активного вибратора» приводит к
смене направления рассеяния излучения, но не приводит к увеличению интенсивности
рассеяния.
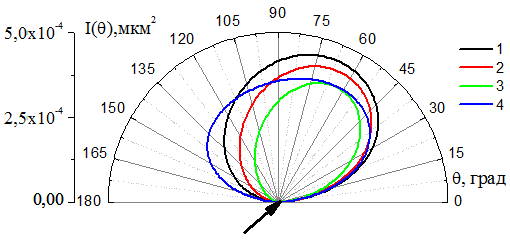
Рис.5. Интенсивность рассеяния на системе «активный вибратор» -
«директор» в
зависимости от угла ![]() между
большей осью
между
большей осью
«вибратора» и осью ![]() .
Расстояние между центрами частиц
.
Расстояние между центрами частиц
![]() нм.
1:
нм.
1: ![]() , 2:
, 2: ![]() ,
3:
,
3: ![]() , 4:
, 4: ![]()
Зависимость рассеянной на системе
«вибратор-директор» интенсивности от расстояния между частицами приводится на
рис. 6. «Вибратор» располагается вдоль оси антенны ![]() .
Расстояние между центрами частиц
.
Расстояние между центрами частиц ![]() последовательно
принимает следующие значения:
последовательно
принимает следующие значения: ![]() нм (кривая 1),
нм (кривая 1), ![]() нм (кривая 2),
нм (кривая 2), ![]() нм (кривая 3),
нм (кривая 3), ![]() нм (кривая 4),
нм (кривая 4), ![]() нм (кривая 5). Из рисунка видно, что
увеличение расстояния между частицами приводит к изменению направления рассеяния
излучения и увеличению интенсивности рассеяния. Причем, в отличие от рассеяния
на системе «вибратор-рефлектор», излучение в направлении падающей волны
происходит при небольших расстояниях, и «в противоположном»- при больших.
нм (кривая 5). Из рисунка видно, что
увеличение расстояния между частицами приводит к изменению направления рассеяния
излучения и увеличению интенсивности рассеяния. Причем, в отличие от рассеяния
на системе «вибратор-рефлектор», излучение в направлении падающей волны
происходит при небольших расстояниях, и «в противоположном»- при больших.
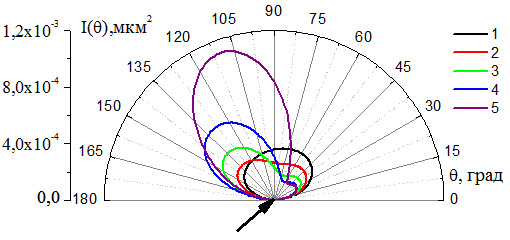
Рис.6. Интенсивность рассеяния на системе «активный вибратор» -
«директор» в зависимости от расстояния между центрами
частиц
![]() .
. ![]() ,
, ![]() . 1:
. 1: ![]() нм,
2:
нм,
2: ![]() нм,
нм,
3: ![]() нм, 4:
нм, 4: ![]() нм, 5:
нм, 5: ![]() нм
нм
Анализируя рассеяние на системах
«вибратор-рефлектор» и «вибратор-директор», можно прийти к следующему
умозаключению. Если располагать «вибратор» вдоль оси антенны ![]() ,
«рефлектор» вдали от «вибратора», а «директоры»- наоборот- поближе, рассеяние
оптической антенной будет происходить в направлении падающей волны.
Предположение было подтверждено в ходе численного эксперимента, результаты
которого представлены на рис. 7. На рисунке приведена интенсивность рассеяния
оптической антенной, состоящей из «активного вибратора», «рефлектора» и трех
«директоров». Расстояния между центрами «вибратора» и «рефлектора», «вибратора»
и ближайшего «директора», и между центрами соседних «директоров» равнялись
соответственно
,
«рефлектор» вдали от «вибратора», а «директоры»- наоборот- поближе, рассеяние
оптической антенной будет происходить в направлении падающей волны.
Предположение было подтверждено в ходе численного эксперимента, результаты
которого представлены на рис. 7. На рисунке приведена интенсивность рассеяния
оптической антенной, состоящей из «активного вибратора», «рефлектора» и трех
«директоров». Расстояния между центрами «вибратора» и «рефлектора», «вибратора»
и ближайшего «директора», и между центрами соседних «директоров» равнялись
соответственно
![]() нм,
нм, ![]() нм,
нм,
![]() нм. Из рисунка видно, что излучение
происходит в направлении падающей волны.
нм. Из рисунка видно, что излучение
происходит в направлении падающей волны.
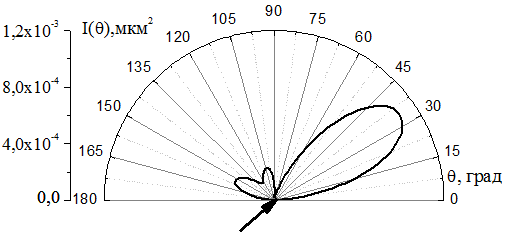
Рис.7. Интенсивность рассеяния на системе «активный вибратор» -
«рефлектор» - три
«директора». ![]() нм,
нм, ![]() нм,
нм, ![]() нм
нм
Если же располагать «рефлектор» вблизи от
«вибратора», а «директоры»- наоборот- подальше, рассеяние оптической антенной
будет происхоть в направлении, «противоположном» направлению падающей волны.
Это предположение также было подтверждено при моделировании рассеяния на той же
системе из пяти частиц. Расстояния между центрами частиц имели значения ![]() нм,
нм, ![]() нм,
нм,
![]() нм. Рассеянная в этом случае интенсивность
изображена на рис. 8. Излучение происходит в направлении, «противоположном»
направлению падающей волны.
нм. Рассеянная в этом случае интенсивность
изображена на рис. 8. Излучение происходит в направлении, «противоположном»
направлению падающей волны.
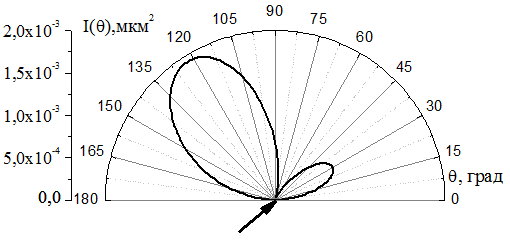
Рис.8. Интенсивность рассеяния на системе «активный вибратор» -
«рефлектор» - три
«директора». ![]() нм,
нм, ![]() нм,
нм, ![]() нм
нм
Заключение
В работе были исследованы характеристики рассеяния
оптической антенной, состоящей из пяти частиц: «активного вибратора»,
«рефлектора» и трех «директоров». Частицы состояли из кремния, располагались в
тонкой пленке из золота, которая была нанесена на поверхность стеклянной призмы.
Антенна возбуждалась плоской электромагнитной волной, распространяющейся под
углом ![]() к оси
к оси ![]() , что приводило к эффекту «экстремального
просачивания энергии» через металлическую пленку, и давало увеличение
интенсивности рассеяния почти на порядок. В ходе численных экспериментов было
установлено, что существует возможность управления направлением интенсивности
рассеянного такой оптической антенной излучения в широком диапазоне. Рассеяние
может происходить как в направлении падающей волны, так и в противоположном.
Направление рассеяния излучения определяется положением «рефлектора» и
«директоров» относительно «активного вибратора».
, что приводило к эффекту «экстремального
просачивания энергии» через металлическую пленку, и давало увеличение
интенсивности рассеяния почти на порядок. В ходе численных экспериментов было
установлено, что существует возможность управления направлением интенсивности
рассеянного такой оптической антенной излучения в широком диапазоне. Рассеяние
может происходить как в направлении падающей волны, так и в противоположном.
Направление рассеяния излучения определяется положением «рефлектора» и
«директоров» относительно «активного вибратора».
Работа выполнена при финансовой поддержке РФФИ, проект № 09-01-00318.
1. Вейко В.П., Вознесенский Н.Б., Воронин Ю.М., и др. Лазерная нанотехнология формирования оптических антенн для ближнепольных микроскопов и исследование их характеристик.// Известия РАН, Сер. Физическая. Т 63, № 11, с.1954-1963, 1999.
2. Bharadwaj P., Deutsch B., Novotny L. Optical antennas.// Advances in Optics and Photonics. 2009. 1 p. 438
3. Q-Han Park. Optical antennas and plasmonics.// Contemporary Physics. 2009. 50 p. 407.
4. Taminiau T.H., Stefani F.D., van Hulst N.F. Enhanced directional excitation and emission of single emitters by a nano-optical Yagi-Uda antenna.// Optics Express. 2008, 16 p. 10858.
5. Hofmann H.F., Kosako T., Kadoya Y. Design parameters for a nano-optical Yagi-Uda antenna.// New Journal of Physics. 2007. 9 p. 217.
6. Hofmann H.F., Kosako T., Kadoya Y. Directional control of light by a nano-optical Yagi-Uda antenna.// Nature Photonics. 2010. 4 p. 312.
7. Ebbesen T.W., Lezec H.J., Ghaemi H.F., et al. // Nature. 1998. 391 p. 667.
8. Wannamacher R. // Opt. Commun. 2001. 195 p. 107.
9. Raether H. Surface plasmon on smooth and rough surfaces and on gratings. B.: Springer. 1988. Ch. 2.
10. Гришина Н.В., Еремин Ю.А., Свешников А.Г. Математическая модель слоистой структуры с наноразмерным отверстием.// Вест. Моск. Ун-та. Сер. 15. Вычисл. Матеем. и Киберн. № 4, с.11-16, 2008.
11. Гришина Н.В., Еремин Ю.А., Свешников А.Г. Эффект экстремального просачивания энергии через проводящую пленку с наноразмерной неоднородностью в области неизлучающих волн.// ДАН. Т 424, №1, с.1-4, 2009.
12. Taflove A., Hagness S. Computational Electrodynamics: The Finite-Difference Time-Domain method. Norwood: Artech House, 2005.
13. Jin J. The Finite Element Method in Electromagnetics. Chichester: John Wiley & Sons, 1993.
14. Eremin Yu.A., Orlov N.V., Sveshnikov A.G. Models of electromagnetic scattering problems based on discrete sources method.// Generalized multipole techniques for electromagnetic and light scattering. Amsterdam: Elsevier Science. 1999. p 39-79.
15. Chew W. C. Waves and fields in inhomogeneous media. New York: IEEE Press, 1995.
16. Еремин Ю.А., Свешников А.Г. Компьютерная технология анализа задач рассеяния методом дискретных источников.// ЖВМиМФ. Т 39, №.12, с.1842-1856, 2000.
17. Дмитриев В.И. Поля в слоистых средах. М.: Изд-во МГУ, 1963. 131 с.
18. Фарафонов В.Г., Ильин В.Б. // Оптика и спектроскопия. 2006. Т. 100. № 3. С.484.
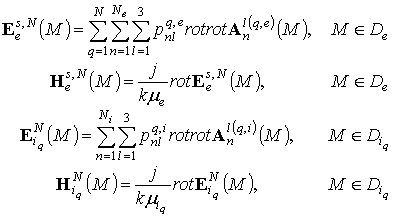 (3)
(3)