Экономичные алгоритмы двумерной Винеровской фильтрации в системах с ортогональными поднесущими.

ЭКОНОМИЧНЫЕ АЛГОРИТМЫ ДВУМЕРНОЙ ВИНЕРОВСКОЙ ФИЛЬТРАЦИИ В СИСТЕМАХ С ОРТОГОНАЛЬНЫМИ ПОДНЕСУЩИМИ

В. М. Смольянинов

Институт радиотехники и электроники им. В.А.Котельникова РАН,
Фрязинcкий филиал

Получена 4 октября 2011 г.

Аннотация. Для мобильных систем передачи дискретных сообщений с ортогональными поднесущими, используя разделимость частотных и временных корреляционных свойств стационарного канала некоррелированных отражателей и аппарат Кронекеровских произведений матриц, обоснованы экономичные вычислительные алгоритмы канального измерителя, реализующие оптимальную двумерную Винеровскую фильтрацию.

Ключевые слова: двумерная Винеровская фильтрация, ортогональные поднесущие, Кронекеровское произведение, канальный измеритель.

Abstract. The effective pilot-based channel estimation algorithms for mobile OFDM systems are grounded in this article. These algorithms are based on two-dimensional Wiener filtering and Kronecker type splitting of spaced-frequency spaced-time correlation function for wide-sense-stationary isotropic scattering channel model.

Key words: OFDM signals, pilot-based channel estimation, two-dimensional Wiener filtering, Kronecker type splitting.

Введение

Сигнально-кодовые конструкции на основе ортогональных поднесущих (orthogonal frequency division multiplexing - OFDM) позволяют просто и весьма эффективно бороться с многолучёвостью с помощью введения на передающей стороне защитного интервала в виде циклического префикса длительностью большей длительности импульсной переходной характеристики канала и в исключении его на приемной стороне. Наилучшие скоростные и вероятностно-энергетические характеристики систем достигаются при когерентном декодировании, которое требует измерения коэффициентов передачи на ортогональных поднесущих. Один из возможных путей построения измерителя основан на использовании пилотных поднесущих с фиксированными частотно-временными позициями и Винеровской фильтрации, которая для мобильных систем приобретает двумерный характер. Построению и анализу эффективности измерителей при таком подходе посвящено множество работ: [6-13] и другие. Целью большинства из них являлось поиск компромисса между сложностью реализации измерителя и его эффективностью. Предлагались различные варианты упрощенной реализации оптимального алгоритма и производилось их сопоставление по сложности и качеству функционирования применительно к стационарному каналу некоррелированных отражателей [5]. При этом исключалась возможность такой организации вычислительной процедуры оптимальной фильтрации, которая упрощает измеритель. Вследствие чего сопоставления не всегда были корректными.

Настоящая работа посвящена обоснованию экономичных вычислительных процедур, реализующих оптимальный алгоритм Винеровской фильтрации. Обоснована возможность разбиения процедуры на два этапа, на первом из которых осуществляется ослабление аддитивных помех, а на втором - восстановление коэффициентов передачи на информационных частотно-временных позициях. И далее для прямоугольной формы пилотных частотно-временных позиций, используя разделимость частотных и временных корреляционных свойств канала и аппарат Кронекеровских произведений матриц, для обоих этапов разрабатываются экономичные вычислительные процедуры.

1. Модель отсчетов на входе канального измерителя

В рассматриваемой системе излучаемое колебание состоит из последовательности OFDM-символов длительностью , содержащих ряд поднесущих, комплексные амплитуды которых манипулируются в соответствии с передаваемой информацией. Поднесущие ортогональны в усиленном смысле на интервале длительностью , меньшей длительности символа на длительность защитного интервала , колебание на котором является циклическим продолжением колебания на интервале ортогональности. Канал передачи сигналов представляется в виде линейного параметрического четырёхполюсника, описываемого изменяющимся во времени t низкочастотным эквивалентом импульсного отклика или его коэффициентом передачи , являющимся преобразованием Фурье от по переменной . Полагается, что на интервале длительностью изменением во времени можно пренебречь так, что сохраняется ортогональность поднесущих на приемной стороне. Кроме того длительность импульсного отклика по переменной полагается меньше длительности защитного интервала , что позволяет путем его исключения на приемной стороне избежать межсимвольной интерференции.

Здесь и в дальнейшем целочисленная переменная будет относиться к оси времени, а переменная - к оси частот.

Амплитуду излучаемой - ой поднесущей на частоте n-го передаваемого символа обозначим через s(n,k). Тогда при сделанных предположениях после разделения ортогональных поднесущих на приемной стороне будем иметь отсчёты , где: , а - независимые отсчёты, обусловленные белым гауссовским шумом. Для когерентного декодирования необходимо знание коэффициента передачи в дискретных частотно-временных позициях, представляемых на плоскости в виде прямоугольной решетки. Ряд фиксированных позиций в этой решетке выделен для пилотных поднесущих, с помощью которых осуществляется оценка коэффициентов передачи на всех позициях. Совокупность () позиций, занимаемых в решетке пилотными поднесущими, будем называть пилотной конструкцией. Сами позиции будем называть активными, а коэффициенты передачи на этих позициях - активными компонентами. Остальные позиции и коэффициенты передачи будем называть пассивными. Будем рассматривать прямоугольную пилотную конструкцию, в которой значения следуют через фиксированный интервал и при каждом значении одновременно излучаются все пилотные поднесущие с номерами .

Для синтеза алгоритмов функционирования измерителя необходимо задать статистические свойства канала передачи сигналов. Будем полагать его стационарным в широком смысле каналом некоррелированных отражателей [5]. В этом случае коэффициент передачи аппроксимируется двумерным гауссовским процессом с нулевым средним и корреляционной функцией [5; 11]

, (1)

где знак < > означает усреднение, а функции и равны единице при нулевых значениях и .

Соотношение (1) иллюстрирует разделимость частотных и временных корреляционных свойств в стационарном канале некоррелированных отражателей и играет важную роль в дальнейших выводах.

Пронормируем входные отсчёты , поделив их на . Кроме того отсчёты на пилотных позициях поделим на , полагая . Тогда на входе канального измерителя будем иметь отсчеты ,где имеют единичные дисперсии, а некоррелированные компоненты имеют дисперсию , обратнопропорциональную отношению сигнал/помеха на активных позициях.

Вектор-столбец активных компонент обозначим через , вектор-столбец всех измеряемых компонент , включая активные, обозначим через и вектор-столбец отсчётов обозначим через , который равен , где - независимый от вектор-столбец независимых помеховых компонент с дисперсиями . Все векторы имеют нулевые средние, а их корреляционные матрицы R R RI полагаются известными. Здесь верхний индекс означает эрмитово сопряжение (транспонирование и комплексное сопряжение), а I - единичная матрица. Элементы вектора имеют единичные дисперсии. Из независимости векторов и имеем RR; RRI.

Будем полагать, что вектор имеет мерность L , а вектора и - мерность .

2. Исходные соотношения

Винеровская фильтрация – это алгоритм линейного комбинирования элементов вектора , обеспечивающий минимум среднеквадратической погрешности оценивания элементов вектора . В общем виде он может быть записан как [1, 2]

=RRRRI). (2)

Он выполняет две функции: ослабление аддитивных помех и восстановление отсчетов на пассивных позициях. Последнюю функцию в дальнейшем будем называть интерполяцией, полагая, что пассивные позиции находятся внутри области задания активных.

Сложность алгоритма оценивают числом операций умножения [10], необходимых для вычисления одной компоненты вектора . Если реализацию осуществлять напрямую в соответствии с (2), то независимо от типа позиции (активной или пассивной) требуемое число операций равно мерности N вектора .

При обратная матрица (RI) всегда существует и при совпадении векторов и решается только задача ослабления аддитивных помех. Используя диагонализацию Эрмитовой матрицы R [3]

R; I, (3)

где - матрица собственных векторов матрицы R, а - диагональная матрица с собственными числами по диагонали, матрица R может быть представлена в виде

RD, (4)

где, в свою очередь, D - диагональная матрица с элементами по диагонали . При реализации вычислений в соответствии с (2) и (4) потребуется умножений на одну компоненту [10], где r - ранг матрицы R.

В отсутствии аддитивных помех ( и ) решается в чистом виде задача интерполяции. При линейной зависимости элементов вектора матрица R будет не обратимой. Ее ранг r будет меньше мерности N , а все элементы вектора могут быть представлены в виде линейной комбинации r его независимых компонент. Соответственно, элементы вектора также могут быть представлены в виде линейной комбинации тех же компонент. Так как независимые компоненты могут быть выбраны множеством способов, то задача интерполяции с минимальной погрешностью имеет множество решений. Для практического применения интерес представляют два решения.

Первое решение получается при дополнительном условии минимальной чувствительности алгоритма к возможным независимым аддитивным помеховым компонентам, которые обуславливают дополнительные погрешности интерполяции. Минимум этих погрешностей имеет место, когда интерполяционные вектор-строки имеют минимальную норму. Можно убедиться, что решение в этом случае имеет тот же вид (2) с заменой обратной матрицы R на псевдообратную R, равную [4] R, где - диагональная матрица с элементами по диагонали

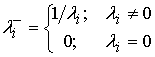
При реализации этого решения вначале будет осуществляться разложение вектора входных отсчётов по собственным векторам матрицы R. При этом достаточно вычислять только коэффициентов разложения, так как эти коэффициенты далее будут домножаться на . После домножения на получится - мерный вектор с ненулевыми компонентами, который далее домножается на матрицу R. В целом на одну компоненту потребуется операций умножения.

Второе решение, наиболее экономичное по числу вычислительных операций, получается путем выбора на этапе проектирования из вектора подвектора с r независимыми компонентами и осуществления интерполяции на основе подвектора . Это решение реализуется с помощью КИХ-фильтра с отводами и потребует умножений на одну позицию.

При соответствующем упорядочивании компонент, вектор в общем случае может быть представлен в виде

P, (5)

где - r-мерный подвектор вектора , r - ранг матрицы R , а P - матрица, состоящая из r столбцов и N строк, первые r строк которой представляют собой единичную матрицу I. Из (5) для корреляционных матриц получаем

RPRP, (6)

RRPRRRP. (7)

Для оценочного вектора активных компонент получаем соотношение
PRP(RI).

Так как первые r строк матрицы P представляют собой единичную матрицу, то верно соотношение

RP(RI), (8)

а вектора и связаны между собой также как и исходные вектора и =P.

В соответствии с (2), (7) и (8) алгоритм оценки всего вектора представляется в виде RR.

Таким образом оценка вектора осуществляется по алгоритму интерполяции, примененному к подвектору оценок отобранных независимых компонент. И, так как вектора и связаны между собой тем же соотношением, что и исходные вектора и , то интерполяцию можно производить с использованием полного оценочного вектора и псевдообратной матрицы R. Алгоритм в целом при этом приобретает вид

RR[R(RI)], (10)

где в квадратных скобках представлен вектор .

Таким образом, из изложенного следует, что оценку всех компонент вектора можно условно разбить на два этапа. На первом осуществляется оценка активных компонент с подавлением аддитивных помех, а на втором - пассивных с использованием алгоритма интерполяции, не зависящего от уровня аддитивных помех.

3. Двумерная интерполяция

Множество активных компонент, занимающих позиции (, прямоугольной пилотной конструкции представим в виде матрицы Z, в которой номера столбцов соответствуют номерам OFDM - символов, а номера строк - номерам поднесущих. Вектор активных компонент упорядочим в порядке последовательного считывания строк (или столбцов) этой матрицы. Не трудно убедиться, что с учетом разделимости корреляционных свойств (1) матрица R может быть представлена в виде Кронекерских произведений [3]

RRR либо RRR (11)

в зависимости от порядка считывания. Матрицы R и R - корреляционные матрицы подвекторов, соответствующих одной строке и одному столбцу матрицы Z, соответственно. Известно [3], что, если существуют обратные матрицы R и R, то

RRR. (12)

При этом собственные вектора матрицы R равны Кронекеровскому произведению собственных векторов матриц Rи R, а собственные числа - произведению собственных чисел и , то есть

R. (13)

Рассмотрим теперь некоторый элемент вектора , находящийся на позиции (n,k). Используя разделимость корреляционных свойств (1), корреляционную вектор-строку матрицы R можно представить в виде

либо , (14)

где - временная корреляционная вектор-строка пассивной компоненты, находящейся на позиции n , с активными компонентами на позициях при фиксированном номере поднесущей, а - частотная корреляционная вектор-строка пассивной компоненты, находящейся на позиции k, с активными компонентами на позициях при фиксированном номере OFDM-символа.

Верхний индекс введен для обозначения векторов-строк.

Используя (11)-(14), в предположении существования обратных матриц R и R можно получить выражение для оптимальной двумерной интерполяционной вектор-строки

R=, (15)

R; R (16)

являются оптимальными одномерными интерполяционными вектор-строками. В отсутствии обратных матриц R и R их следует заменить на псевдообратные R и R .

Пусть вектор получен путем построчного считывания матрицы Z активных компонент, т.е. он состоит из последовательности подвекторов , соответствующих j -ым строкам матрицы. Тогда интерполяционное значение элемента будет вычисляться в соответствии с соотношением

, (17)

где вектор-столбец состоит из элементов

v. (18)

Таким образом алгоритм двумерной интерполяции реализуется путем последовательного применения двух одномерных.

Обозначим через R и R интерполяционные матрицы, состоящие из интерполяционных строк и , соответственно. Тогда для интерполяционного значения вектора в целом будем иметь соотношение

RR=(RR. (19)

Рассмотрим блок из N OFDM - символов c K поднесущими в каждом. Тогда в матричном представлении X вектора будет содержаться столбцов и строк. Пилотная конструкция в блоке содержит временных и частотных позиций. Полагаем, что обратные матрицы R и R существуют. Матрица R будет состоять из строк () длительностью каждая, а матрица R - из строк ( ) длительностью каждая. Вектора-столбцы () будут содержать элементов.

Если вычисляется только одно интерполяционное значение в соответствии с (17) и (18 ), то понадобится умножений, т. е. больше чем мерность вектора . Однако величины v (18 ) могут быть использованы для вычисления интерполяционных значений на всех частотных позициях . С учетом этого требуемое количество умножений на одну позицию существенно сокращается.

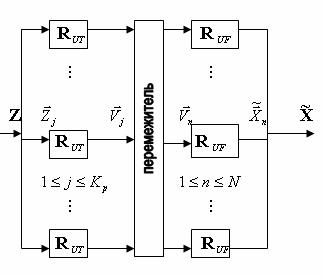
Рис.1. Блок-схема двумерного интерполятора.

На рисунке 1 представлена блок-схема двумерного интерполятора, осуществляющего интерполяцию всего вектора (матрицы X) при последовательном считывании строк матрицы активных компонент Z. Подвектора-столбцы () имеют мерность . Они домножаются слева на матрицу R, содержащую строк и столбцов, в результате получаются подвектора-столбцы мерностью . Совокупность этих подвекторов образуют матрицу V, содержащую строк и столбцов. В перемежителе производится последовательное считывание строк этой матрицы, образуя вектора-столбцы (), фигурирующие в соотношении (17). Их мерность равна . Эти вектора домножаются слева на матрицу R, содержащую строк и столбцов. В результате получаются интерполяционные подвектора () мерностью . Совокупность этих векторов образуют матрицу интерполяционных значений .

Не трудно убедиться, что требуемое число операций умножения на одну позицию в этой схеме при полных рангах матриц R и R равно

. (20а)

При последовательном считывании столбцов матрицы Z активных компонент вначале будет производиться домножение слева подвекторов-столбцов на матрицу R , а затем - на матрицу R. Число операций умножения на одну компоненту при этом будет равно

. (20б)

В любом случае, эти величины (20а и 20б) значительно меньше числа операций , необходимых при реализации интерполятора в соответствии с исходным соотношением (2). Кроме того, при заданных параметрах сигнально-кодовой конструкции можно, исходя из соотношений (20а) и (20б), выбрать наиболее экономичный вариант формирования вектора из матрицы активных компонент Z.

При неполных рангах и матриц R и R, соответственно, требуемое число операций умножения зависит от типа одномерных интерполяторов и варианта формирования вектора . Если одномерные интерполяторы строятся на основе КИХ-фильтров с и отводами по времени и частоте, то при построчном считывании матрицы Z требуемое число умножений на одну позицию равно . При считывании матрицы Z по столбцам требуемое число умножений будет равно . Если одномерные интерполяторы строятся на основе псевдообратных матриц и матрица Z считывается построчно, то число операций будет равно

4. Двумерная оценка активных и пассивных компонент

При оценке активных компонент, вектор в соотношении (2) следует заменить на вектор и, соответственно, матрицу R - на матрицу R. Алгоритм оценки активных компонент можно упростить, используя диагонализацию Эрмитовых матриц [3]. При последовательном считывании строк матрицы Y для формирования вектора алгоритм оценки можно записать в виде

D, (21)

где D - диагональная матрица с элементами по диагонали
.

Сопоставляя (21) с (19) видим, что алгоритм оценки активных компонент состоит из двух частей, каждая из которых аналогична алгоритму двумерной интерполяции. На рисунке 2 представлена блок-схема устройства, осуществляющего оценку активных компонент, которая получена с учётом следующего легко проверяемого соотношения

[], (22)

где вектор формируется последовательным считыванием строк его матричного представления V, а - последовательным считыванием столбцов. Т.е. индекс означает перемежение.

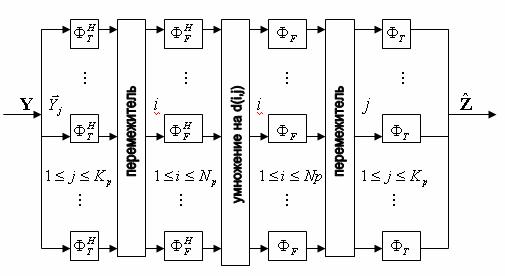
Рис.2. Блок-схема двумерного оценивателя активных компонент.

В схеме подвектора-столбцы () формируются последовательным считыванием строк матрицы Y. При последовательном считывании столбцов этой матрицы на входе будут подвектора-столбцы () и последовательность матричных умножителей сменится на противоположную ().

Прямая реализация соотношения (2) для оценки активных компонент при полном ранге матрицы R потребует операций умножения на каждую компоненту, а представленная схема - операций. Если ранги и матриц R и R меньше их мерности, то число операций сократится до величины 2(.

В соответствии с изложенным ранее, оценка пассивных компонент осуществляется путём интерполяции оценочного вектора активных компонент, которую можно реализовать либо на основе КИХ-фильтров либо с использованием псевдообратной матрицы R. В последнем случае процессы оценки активных компонент и интерполяции можно объединить в единый процесс. Действительно, используя соотношение (10) и диагонализацию матриц, для оценочного значения вектора можно получить соотношение

GG)D, (23)

где матрицы G и G состоят из векторов-строк и ,соответственно, а матрица D - диагональная с элементами по диагонали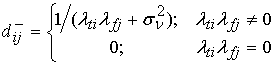

Сопоставляя (21) и (23), видим, что блок-схема, реализующая соотношение (23), аналогична блок-схеме рис. 2.

Заключение

Таким образом, в работе для прямоугольной пилотной конструкции, используя разделимость частотных и временных корреляционных свойств стационарного канала некоррелированных отражателей, обоснованы экономичные вычислительные процедуры оптимальной двумерной Винеровской фильтрации, существенно упрощающие канальный измеритель в мобильной системе связи с ортогональными поднесущими. Полученные оценки для числа операций умножения, необходимого при реализации различных соотношений, позволяют выбирать наиболее экономичный вариант построения канального измерителя при заданных параметрах сигнально-кодовой конструкции.

Литература

1. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов: Пер. с англ. М.: Связь, 1980.

2. Цифровая обработка изображений в информационных системах: Учеб. Пособие: И.С. Грузман, В.С. Киричук и др.: Новосибирск: НГТУ, 2002.

3. Беллман Р. Введение в теорию матриц: Пер. с англ. М.: Наука, 1976.

4. Марпл-мл. С.А. Цифровой спектральный анализ и его приложения: Пер. с англ. М.: Мир, 1990.

5. Bello P. Characterization of randomly time-variant linear channels// IEEE Trans. On Comm., vol. Cs-11, Dec. 1963, pp. 360-393.

6. Cavers J.K. An analysis of pilot symbol assisted modulation for Rayleigh fading channels// IEEE Trans. On Veh. Techn., Vol. 40, №4, November 1991.

7. Van de Beek J.-J., Edfors O. et al. On channel estimation in OFDM systems// in Proc. IEEE Veh. Techn. Conf., Vol. 2, pp. 815 – 819, Chicago, IL, July 1995.

8. Sandell M., Edfors O. A comparative study of pilot-based channel estimators for wireless OFDM// Div. Signal Processing, Lulea Univ. Technology, Lulea, Sweden, Res. Rep. TULEA 1996: 19, Sept. 1996.

9. Nilsson R., Edfors O., Sandell M., Borjesson P.O., An analysis of two-dimensional pilot-simbol assisted modulation for OFDM// Div. Signal Processing, Lulea Univ. Technology, S – 971 87 Lulea, Sweden.

10. Edfors O., Sandell M. et al. OFDM channel estimation by singular value decomposition// IEEE Trans. On Comm., Vol. 46, July 1998.

11. Li Y., Cimini L.J., Sollenberger N.R. Robust channel estimation for OFDM systems with rapid dispersive fading channels// IEEE Trans. On Comm., Vol. 46, July. 1998.

12. Yang B., Cao Z., Letaief K.B. Analysis of low-complexity windowed DFT-based MMSE channel estimator for OFDM systems// IEEE Trans. On Comm., Vol. 49, November, 2001.

13. Каюков И.В., Манелис В.Б. Оценка канала в мобильных системах связи OFDM// Мобильные системы, 2005, №10, с. 20 - 24.