УДК 537.8
КОМПЛЕКСНЫЙ ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ РУДНЫХ МИНЕРАЛОВ В МИКРОВОЛНОВОМ ДИАПАЗОНЕ
А. Л. Дзарданов1, В. В. Тихонов2, Д. А. Боярский2, О. Н. Полякова1, Г. Н. Гольцман1
1Московский педагогический государственный университет,
2 Институт космических исследований РАН
Получена 25 сентября 2012 г.
Аннотация. В работе приводятся результаты исследований комплексной диэлектрической проницаемости ряда рудных минералов (магнетит, гематит, сфалерит, халькопирит, пирит и ильменит) и сопутствующих им нерудных минералов (лабрадор и олигоклаз). Описываются методы измерения отражательной и пропускательной способности плоскопараллельных образцов минералов в диапазоне частот 12...145 ГГц, а также способы и результаты расчета диэлектрических характеристик минералов из полученных экспериментальных данных. Приводятся аппроксимационные выражения для расчета действительной и мнимой части комплексной диэлектрической проницаемости минералов в зависимости от частоты излучения в диапазоне 12...145 ГГц.
Авторы высказывают искреннюю признательность компаниям ООО «ТЕХНОРОС» и ООО «РАДОС» г. Красноярска за предоставленные образцы минералов.
Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг, а также при поддержке РФФИ (проект № 10-05-00037).
Ключевые слова: электродинамическая модель, минералы, микроволновое излучение, отражательная способность, пропускательная способность, комплексная диэлектрическая проницаемость.
Abstract: The paper discusses results of studies of complex dielectric permittivity of a number of ore minerals (magnetite, hematite, sphalerite, chalcopyrite, pyrite and ilmenite) and associate barren minerals (labradorite and oligoclase) in copper ore. Techniques to measure the reflection power and transmission coefficient of plain-parallel samples of minerals in the frequency range of 12....145 GHz are described, as well as computation methods and results for dielectric characteristics of the minerals based on the obtained experimental data. Approximation expressions are presented for the real and imaginary parts of complex dielectric permittivity of the minerals depending on radiation frequency in the range of 12…145 GHz.
Authors express sincere gratitude to the companies of Open Company TECHNOROS and Open Company RADOS (Krasnoyarsk) for given samples of minerals.
The work was supported by FTP "Scientific and scientific-pedagogical personnel of innovative Russia" for 2009-2013 years, by the Russian Foundation for Basic Research (project N 10-05 00037).
Key words: electrodynamic model, minerals, microwave radiation, reflectivity, transmissivity, complex dielectric permittivity.
Введение
Дистанционные методы исследования поверхности Земли и планет находят практическое применение в разнообразных областях хозяйствования и научных исследований. В последнее время аэрокосмическое зондирование широко используется в поисковой и инженерной геологии: поиск полезных ископаемых, исследование состояния дамб, подземных объектов и т. п. [1-4]. Одной из проблем, препятствующих развитию этого направления, является недостаточная исследованность диэлектрических характеристик горных пород и слагающих их минералов в микроволновом диапазоне [5-7].
1. Методика измерений
1.1. Характеристики образцов минералов.
Для проведения измерений были подготовлены образцы следующих минералов: магнетита (Fe3O4), халькопирита (CuFeS2), пирита (FeS2), гематита (Fe2O3), сфалерита (ZnS) и ильменита (FeTiO3). Все минералы имеют относительно малое удельное сопротивление на низких частотах (10-5...106 Ом·м) и считаются полупроводниками [5]. Также были подготовлены образцы двух нерудных минералов, относящихся к серии плагиоклазов: лабрадора и олигоклаза (изоморфная смесь альбита — Na[AlSi3O8] и анортита — Ca[Al2Si2O8] в различных концентрациях). Оба эти минерала являются типичными представителями несущей породы (породообразующими минералами). Они имеют высокое удельное сопротивление на низких частотах (1011...1012 Ом·м) и считаются диэлектриками [5]. Исследуемые образцы представляли собой сростки нескольких кристаллов одного минерала с небольшими примесями других минералов. Для рудных минералов количество пор (мелких пустот) и примесей нерудных минералов (кварц, плагиоклазы) у каждого образца не превышало 10 %. Для нерудных минералов количество примесей рудных минералов также не превышало 10 %.
1.2 Диапазон частот 12...38 ГГц.
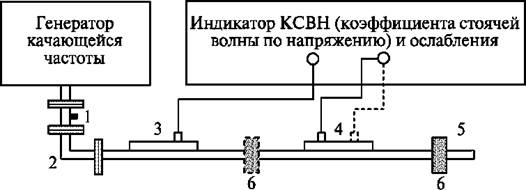
Частотные зависимости отражательной R(f) и пропускательной T(f) способности плоскопараллельных образцов минералов в диапазоне частот 12...38 ГГц измерялись на панорамном измерителе коэффициента стоячей волны и ослабления: Р2-67 (диапазон частот 12…17 ГГц), Р2-66 (диапазон частот 17…26 ГГц), Р2-65 (диапазон частот 25…38 ГГц). Для проведения измерений образцы изготавливались под волноводную ячейку № 1 размером 11*5,5 мм (диапазон 17...26 ГГц) и ячейку № 2 размером 16*8 мм. (диапазон 12...17 ГГц). Для диапазона частот 25…38 ГГц использовался волноводный переход с ячейки № 1 на волновод размером 8*3,6 мм. Схема экспериментальной установки для измерения коэффициента стоячей волны и ослабления приведена на рис. 1.
|
|
Рис. 1. Схема панорамного измерителя коэффициента стоячей волны и ослабления: 1 — аттенюатор; 2 — волноводный переход; 3 — направленный ответвитель падающей волны; 4 — направленный ответвитель отраженной волны; 5 — согласованная нагрузка; 6 — образец. Пунктир — расположение элементов при измерении ослабления.
В основу панорамных измерителей положен принцип раздельного выделения и непосредственного детектирования сигналов падающей и отраженной волны. При измерении отражения (рис. 1) сигнал, пропорциональный амплитуде напряжения волны, падающей на исследуемый образец, выделяется направленным ответвителем падающей волны. Сигнал, отраженный от исследуемого образца, выделяется направленным ответвителем отраженной волны. По шкальному устройству производится непосредственный отсчет коэффициента стоячей волны по напряжению ρ. Отражательная способность R определяется как:
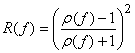 (1)
(1)
При измерении пропускания определяется ослабление сигнала (в дБ), прошедшего через образец, которое потом пересчитывается в пропускательную способность T. В эксперименте удавалось измерять значения Т до 10-4. Погрешность измерений R и T не превышала 5 %.
В ходе эксперимента были получены зависимости R(f) и T(f) для трех рудных минералов: халькопирита, пирита и магнетита, а также для лабрадора (рис. 2).
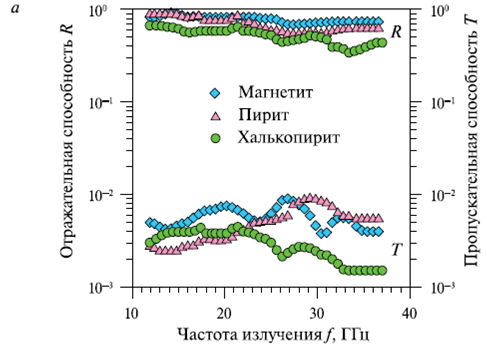
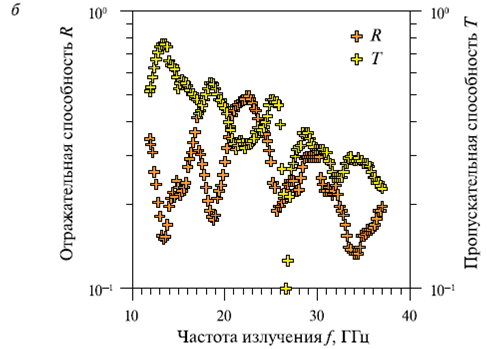
Рис. 2. Спектральные зависимости R(f) и T(f) в диапазоне частот 12…38 ГГц для образцов трех рудных минералов (а) и лабрадора (б). Толщина образцов (см): магнетит — 0,55; пирит — 0,48; халькопирит — 0,57; лабрадор — 0,665.
1.3. Диапазон частот 77…145 ГГц
Зависимости R(f) и T(f) образцов минералов в диапазоне частот 77...145 ГГц измерялись с помощью миллиметрового спектрометра, собранного на лампах обратной волны (миллиметровый ЛОВ-спектрометр). Спектрометр состоял из генератора, измерительного квазиоптического тракта и приемного блока (рис. 3).
В качестве источников монохроматического электромагнитного излучения использовались: в диапазоне частот 77…119 ГГц — генератор РГ4-14 (ЛОВ-71), а в диапазоне частот 126...145 ГГц — генератор Г4-161 (ЛОВ-76).
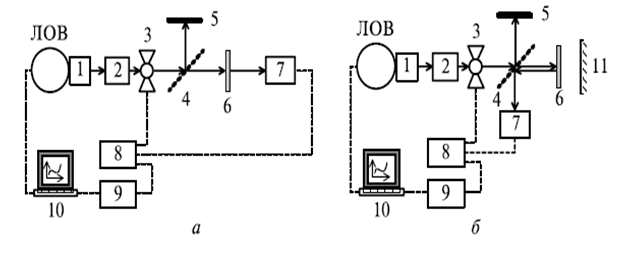
Рис. 3. Блок-схема миллиметрового ЛОВ-спектрометра: а — измерение T(f); б — измерение R(f): 1 — рупор/волноводно-лучеводный переход; 2 — аттенюатор; 3 — модулятор; 4 — делитель луча; 5 — поглотитель; 6 — исследуемый образец; 7 — оптико-акустический преобразователь; 8 — синхродетектор; 9 — цифровой вольтметр; 10 — компьютер; 11 — зеркало.
Измерительный квазиоптический тракт спектрометра был собран на базе лучеводов, которые обеспечивали одномодовое распространение электромагнитной волны путем поглощения остальных типов волн в диэлектрике с потерями.
Приемный блок состоял из приемника — ячейки Голея (приемный элемент оптико-акустического преобразователя), синхродетектора и цифрового вольтметра Agilent 34401 A.
Выходящее из ЛОВ монохроматическое излучение с помощью рупора (диапазон частот 77…119 ГГц) или волноводно-лучеводного перехода (диапазон частот 126...145 ГГц) поступало в измерительный тракт. Далее электромагнитное излучение модулировалось по амплитуде механическим модулятором с частотой 12,5 Гц и затем по квазиоптическому тракту подводилось к приемному блоку.
При измерении спектра пропускания образец помещался в держателе так, чтобы излучение падало на него нормально, а сам образец полностью перекрывал отверстие лучевода (см. рис. 3а). Электромагнитное излучение падало на слюдяную делительную пластину толщиной 0,03 мм. В частотном интервале 77…145 ГГц коэффициент пропускания пластины составлял 50 %. Часть излучения проходила через делительную пластину в измерительный канал, через исследуемый образец и фиксировалась приемником. Часть излучения отражалась от делительной пластины и поступала во второе плечо схемы. Там находился поглотитель, за счет которого не возникало побочных резонансов из-за переотражения на делителе луча.
Перед началом измерений проводилась калибровка установки при отсутствии в держателе исследуемого образца. Уровень мощности падающего на приемник микроволнового излучения уменьшался калиброванным поляризационным аттенюатором, позволяющим ослаблять сигнал на 30 дБ.
Спектр пропускания T(f) записывался в два этапа. Сначала снималась частотная зависимость мощности сигнала без образца в держателе измерительного тракта P1(f), затем мощность сигнала при наличии образца в измерительном тракте P2(f). Абсолютная величина пропускательной способности образца получалась делением двух массивов чисел:
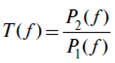 (2)
(2)
В эксперименте удавалось измерять значения Т до 10-7.
Спектр отражения R(f) также определялся в два этапа. Вначале снималась частотная зависимость мощности сигнала, отраженного от калибровочного зеркала P3(f), установленного в держателе на месте образца (см. рис. 3б). Сигнал отражался от делителя луча и фиксировался приемником. Затем снималась частотная зависимость мощности сигнала, отраженного от образца, установленного на месте зеркала P4(f). Абсолютная величина отражательной способности образца получалась делением двух соответствующих массивов чисел:
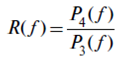 (3)
(3)
Основные параметры спектрометра, используемого в эксперименте: мощность рабочего излучения — 4…6 мВт; относительное частотное разрешение — Δν/ν ~ 10-4; отношение сигнал/шум — 104…106; эквивалентная мощность шума (NEP) —10-10 Вт/Гц0,5; динамический диапазон — не менее 60 дБ; вольт- ваттная чувствительность —105 В/Вт; степень поляризации рабочего излучения — 99,99%. Погрешность измерений составляла не более 3 %.
Результаты спектральных измерений R(f) и T(f) всех исследуемых минеральных образцов представлены на рис. 4 и рис. 5.
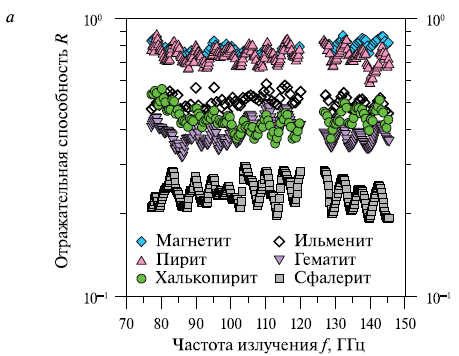
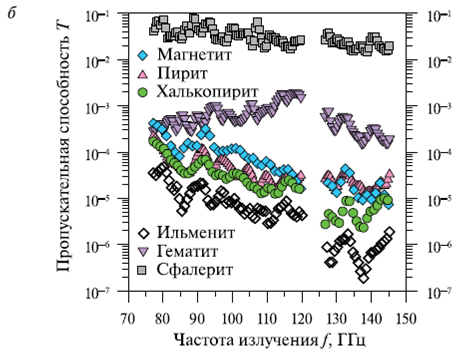
Рис. 4. Спектральные зависимости R(f) (а) и T(f)
(б) в диапазоне частот 77…145 ГГц для образцов рудных минералов. Толщина
образцов (см): магнетит — 1,283; пирит — 1,275; халькопирит — 1,33; ильменит —
2,01; гематит — 1,98; сфалерит — 1,963
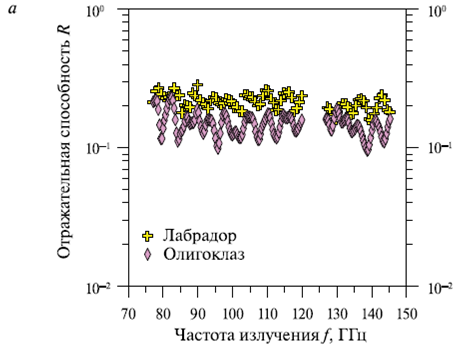
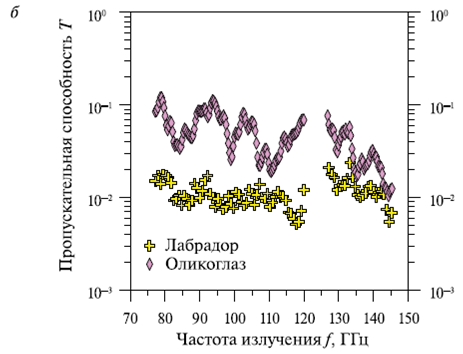
Рис. 5. Спектральные зависимости R(f) (а) и T(f) (б) в диапазоне частот 77...145 ГГц для образцов нерудных минералов. Толщина образцов (см): лабрадор — 1,28; олигоклаз — 1,32
2. Расчет диэлектрических характеристик
Для определения действительной ε' и мнимой ε'' части комплексной диэлектрической проницаемости ε (ε = ε' + i·ε") минералов из экспериментальных спектральных зависимостей R(f) и T(f) была рассмотрена следующая задача (рис. 6): на плоскопараллельный слой вещества (среда 2), находящийся в вакууме (среда 1), под углом Θ = 0°, падает плоская электромагнитная волна с интенсивностью I0. Слой имеет толщину h и комплексный показатель преломления n = n' + i·n" . Интенсивности излучения IR и IT, отраженного от слоя и прошедшего сквозь слой, с учетом многократного отражения от границ будут определяться следующими соотношениями [8]
![]() , (4)
, (4)
где R и T — отражательная и пропускательная способность, которая связана с коэффициентами отражения r и пропускания t следующим образом [8]:
где 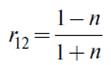 — коэффициент отражения от границы раздела вакуум-вещество;
— коэффициент отражения от границы раздела вакуум-вещество;
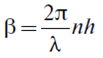 , λ — длина волны
излучения.
, λ — длина волны
излучения.
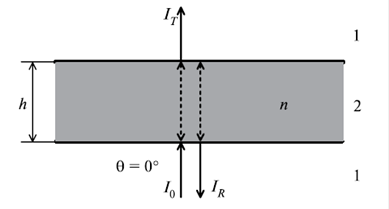
Рис. 6. Схема задачи
Действительная и мнимая части комплексной диэлектрической проницаемости связана с действительной и мнимой частями комплексного показателя преломления следующими соотношениями:
Для определения n' и n" вещества необходимо решить систему уравнений (5). Эта система уравнений не поддается аналитическому решению и решается численными методами. Каждый диапазон, в котором были получены зависимости R(f) и T(f) минералов (12…38 и 77...145 ГГц), был разбит на одинаковые небольшие частотные интервалы шириной Δf. Предполагалось, что в частотном интервале Δf действительная и мнимая части комплексного показателя преломления минерала остаются постоянными. В каждом интервале частот Δf, путем минимизации целевой функции F(n', n") определялись значения n' и n". Целевая функция
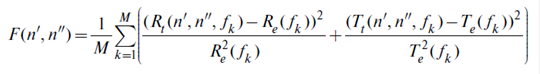 (7)
(7)
представляла собой сумму квадратов коэффициентов вариации теоретических зависимостей отражательной и пропускательной способности в интервале частот Δf. В выражении (7): fk — частота излучения в интервале Δf; Rt(n', n", fk) и Tt(n', n", fk) — теоретически рассчитанные из (5) значения отражательной и пропускательной способности при заданных параметрах оптимизации n' и n" на частоте излучения fk; Re(fk) и Te(fk) — экспериментальные значения отражательной и пропускательной способности при той же частоте излучения; M — количество экспериментальных точек в интервале частот Δf.
Для минимизации целевой функции был применен метод Розенброка [9]. Этот метод представляет собой типичный метод поиска, в котором направления минимизации полностью определяются на основании последовательных вычислений целевой функции. Метод Розенброка был успешно применен авторами при определении структурных параметров сухих песчаников [10, 11]. Алгоритм вычислений имел следующий вид:
1. Задавались разумные ограничения на n' и n": 1 < n' < 50, n">0;
2. Для диапазона 12…38 ГГц выбирался интервал Δf = 2 ГГц, для диапазона 77…145 ГГц — Δf = 5 ГГц. На каждом участке Δf задавалось значение n' с шагом 0,01 от 1 до 50. При этих значениях минимизировалась целевая функция (7) и определялось значение n".
3. С помощью полученного массива n' и n", на интервале Δf, из (5) определялись теоретические R и T, которые сравнивалась с экспериментальными R и T. Наилучшее совпадение теоретических и экспериментальных R и T давало конечные величины n' и n".
Найденные значения n' и n" аппроксимировались гладкими функциями от частоты излучения. Ниже приведены полученные аппроксимационные выражения n' и n" для всех исследованных минералов:
магнетит, диапазон 12...145 ГГц:
пирит, диапазон 12...145 ГГц:

халькопирит, диапазон 12...145 ГГц:
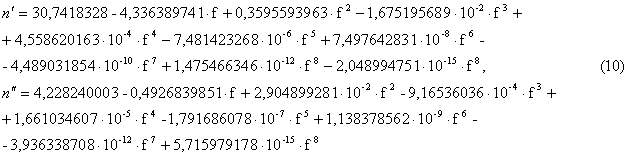
сфалерит, диапазон 12...145 ГГц:
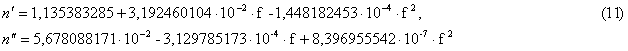
ильменит, диапазон 12...145 ГГц:
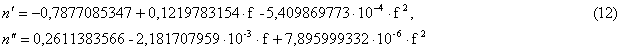
гематит, диапазон 12...145 ГГц:

лабрадор, диапазон 12...145 ГГц:

олигоклаз, диапазон 12...145 ГГц:
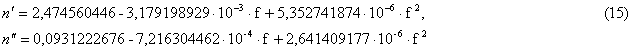
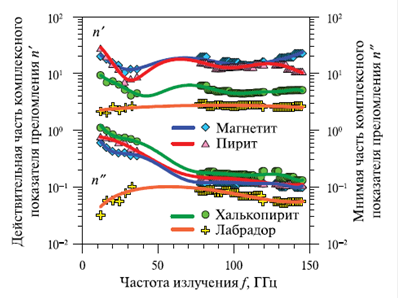
Рис. 7. Частотные зависимости
действительной и мнимой частей комплексного показателя преломления магнетита,
пирита, халькопирита и лабрадора в диапазоне 12...145 ГГц. Символы — значения,
полученные при использовании вычислительного алгоритма, кривые — аппроксимации
полученных значений.
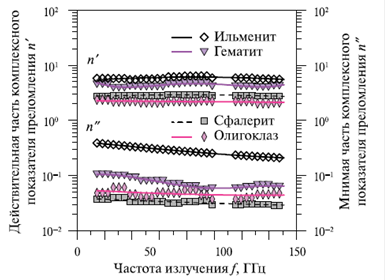
Рис. 8. Частотные зависимости
действительной и мнимой частей комплексного показателя преломления ильменита,
гематита, сфалерита и олигоклаза в диапазоне 12...145 ГГц. Символы — значения,
полученные при использовании вычислительного алгоритма, кривые — аппроксимации
полученных значений.
В выражениях (8)—(15) f — частота излучения, выраженная в гигагерцах.
Действительная ε' и мнимая ε'' части комплексной диэлектрической проницаемости минералов вычисляются из выражений (6), в которых значения n' и n" определяются из (8)—(15). Приведенные аппроксимационные функции могут быть использованы для вычисления n' и n" или ε' и ε'' минералов в соответствующем диапазоне частот.
На рис. 7 и рис. 8 представлены значения действительной и мнимой частей комплексного показателя преломления минералов, полученные из экспериментальных данных при численном решении системы уравнений (5), а также аппроксимационные зависимости этих значений, рассчитанные из выражений (8)—(15).
3. Выводы
В данной работе были исследованы отражательные и пропускательные характеристики рудных и нерудных минералов в микроволновом диапазоне электромагнитных волн. В процессе проведенных исследований были получены аппроксимационные выражения для действительной и мнимой частей комплексного показателя преломления ряда минералов в диапазоне частот 12…145 ГГц.
Литература
1. Яковлев О. И. Космическая радиофизика. М.: Науч. кн., 1998. 432 с.
2. Sharkov E.A. Passive Microwave Remote Sensing of the Earth: Physical Foundations. Chichester, UK: Springer/PRAXIS, 2003. 612 p.
3. Быстров Р. П., Загорин Г. К., Соколов А. В., Фёдорова Л. В. Пассивная радиолокация: методы обнаружения объектов. М.: Радиотехника, 2008. 320 с.
4. Цымбал В. Н., Яцевич С. Е., Ефимов В. Б., Курекин А. С., Матвеев А. Я., Гавриленко А. С., Бычков Д. М. Использование многочастотных радиолокационных данных для выявления геологических структур и месторождений полезных ископаемых дистанционными методами // Соврем. проблемы дистанц. зондирования Земли из космоса. 2010. Т. 7. № 2. С. 354-360.
5. Справочник физических констант горных пород / Под ред. С. Клар¬ка. М.: Мир, 1969. 544 с.
6. CampbellM. J., Ulrichs J. Electrical properties of rocks and their signifi¬cance for lunar radar observations // J. Geophysical Research. 1969. V. 74. N. 25. P. 5867-5881.
7. Романов А. Н. Экспериментальные исследования диэлектрических свойств почвообразующих минералов и минеральных солей в микро¬волновом диапазоне. Барнаул: АГУ, 2002. 50 с.
8. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720 с.
9. ХиммельблауД. М. Прикладное нелинейное программирование. М.: Мир, 1975. 534 с.
10. Боярский Д. А., Гершензон В. Е., Гершензон Е. М., Гольцман Г. Н., Пти- цина Н. Г., Тихонов В. В., Чулкова Г. М. О возможности определения микроструктурных параметров нефтеносной породы по данным радиофизических измерений // Радиотехника и электроника. 1996. Т. 41. № 4. С. 441-447.
11. Boyarskii D.A. Method of Retrieval of Media Structural Parameters from Frequency Dependence of Transmission Coefficient // Intern. Geoscience and Remote Sensing Symp. (IGARSS'96): Proc. 1996. V. 2. P. 1349-1351.
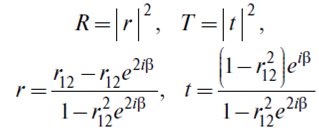 , (5)
, (5)