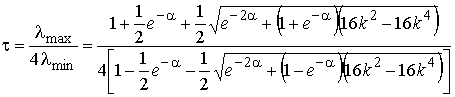Многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах.

УДК 681.513.6

МНОГОКАНАЛЬНЫЙ АДАПТИВНЫЙ КОМПЕНСАТОР СО СЛЕПЫМ РАЗДЕЛЕНИЕМ ПОМЕХ В ОПОРНЫХ КАНАЛАХ

А. Е. Манохин

Институт радиоэлектроники и информационных технологий-РТФ УрФУ им. первого Президента РФ Б.Н.Ельцина, кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург

Статья получена 15 октября 2014 г.

Аннотация. В статье представлен многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах. Благодаря разделению помех обусловленность корреляционной матрицы помех улучшается, а скорость сходимости адаптивного алгоритма наименьших квадратов увеличивается. При этом выигрыш в скорости сходимости при использовании модифицированного алгоритма слепого разделения Жуттена-Эро составляет не менее 6 раз.

Ключевые слова: слепое разделение сигналов, многоканальный адаптивный компенсатор, модифицированный алгоритм Жуттена-Эро, скорость сходимости.

Abstract: In the paper the multichannel adaptive canceller with blind disturbances separation in reference channels is presented. Thanks to disturbances separation conditionality of a disturbances correlation matrix improves, and convergence rate of least mean square algorithm increases. Thus using modified Jutten–Herault algorithm the gain of convergence rate equals not less than 6 times.

Key words: blind sources separation, multichannel adaptive canceller, modified Jutten–Herault algorithm, convergence rate.

Введение

Многоканальные автокомпенсаторы помех целесообразно применять в тех случаях, когда необходимо скомпенсировать помехи, приходящие из нескольких точек, и можно получить несколько линейных независимых компенсационных колебаний, представляющих собой смесь помех [1]. Структурная схема многоканального адаптивного компенсатора Уидроу изображена на рис. 1. Для наглядности представления пренебрежем некоррелированными шумами в основном и опорном каналах, а число помех N выберем равное числу входов опорного канала. Помехи проходят через внешний канал до основного канала пути с коэффициентами передачи F_i(jw), а в опорный проходят пути с коэффициентами передачи G_ij(jw).

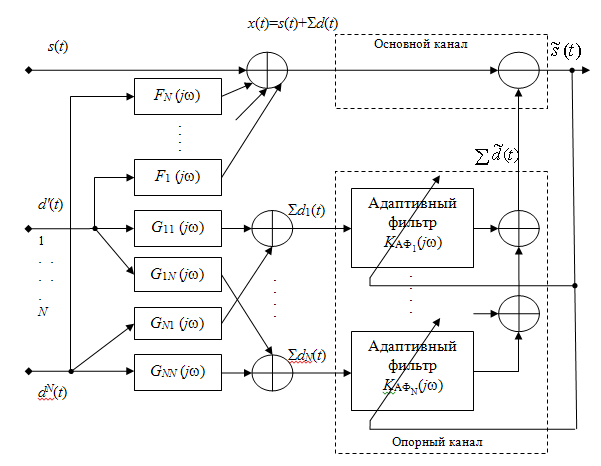
Рис. 1. Структурная схема многоканального адаптивного компенсатора Уидроу.

Если на каждом входе опорного канала действовала бы только одна помеха, то задача адаптации была бы тривиальна в том смысле, что каждый адаптивный фильтр отслеживал бы только одну помеху по критерию минимизации СКО. Однако задача адаптации в данном случае решается сложнее.

Так имеется смешивающая матрица помех:

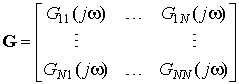, (1)

где G_ij(jw) — передаточная функция от источника i ко входу j.

Определим вектор передаточных функций от источника помехи к i-му входу:

. (2)

Если определить W как вектор оптимальных передаточных функций

, (3)

тогда [2]:

(4)

Однако недостатком такого решения задачи является то, что, во-первых, обратная матрица G может и не существовать на всех частотах [2], а во-вторых, в процессе адаптации весовых коэффициентов может наблюдаться их медленная сходимость к оптимальным значениям из-за плохой обусловленности корреляционной матрицы помех и в связи с тем, что адаптация является взаимозависимой во всех каналах.

Постановка задачи

Наиболее распространенным критерием оценки весовых коэффициентов фильтров в многоканальном адаптивном компенсаторе является минимум среднего квадрата ошибки, а самым простым в алгоритмической реализации и с минимальной вычислительной сложностью методом поиска значений этих коэффициентов — метод наименьших квадратов:

(5)

где m — параметр адаптации, который определяет скорость и устойчивость процесса адаптации; X — вектор входного сигнала адаптивного фильтра в опорных каналах; W— вектор весовых коэффициентов адаптивного фильтра в опорных каналах; e — выходной сигнал многоканального компенсатора.

Обусловленность матрицы влияет на постоянную времени обучающей кривой и, как следствие, на скорость сходимости алгоритма. Число обусловленности c для симметричных положительно определенных матриц есть отношение их максимального и минимального собственных чисел [3].

Максимальное значение постоянной времени обучающей кривой для алгоритма наименьших квадратов в случае действительных весовых коэффициентов находится [4]:

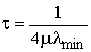(6)

где l_min — минимальное собственное число корреляционной матрицы входного сигнала адаптивного фильтра.

В выражении (6) параметр адаптации m зависит от максимального собственного числа [2]:

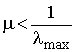, (7)

поэтому максимальное значение постоянной времени обучающей кривой не может быть меньше четверти отношения максимального и минимального собственных чисел корреляционной матрицы или четверти ее числа обусловленности:

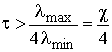(8)

Определим значение постоянной времени обучающей кривой для многоканального адаптивного фильтра через уравнение собственных значений:

(9)

R — корреляционная матрица помех; I — единичная матрица.

Для простоты возьмем для рассмотрения двухканальный вариант реализации адаптивного компенсатора помех. В опорном канале действует смесь помех — белого гауссова шума n₀(n) и гауссово-марковского процесса d(n) с относительной шириной полосы a:

— в 1 опорном канале; (10)

— во 2 опорном канале, (11)

где k и — СКО помех в каналах.

Составим корреляционную матрицу помех в опорном канале:

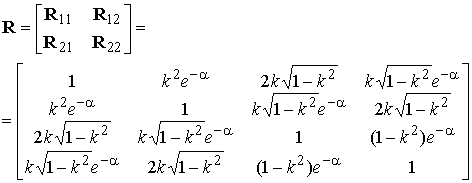(12)

Тогда уравнение собственных значений (9):

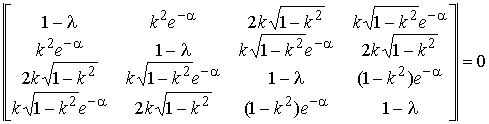(13)

Решая систему уравнений (13) относительно l, получаем:

(14)

Рисунок 2 демонстрирует наихудшую обусловленность матрицы и, как следствие, наибольшую постоянную времени обучающей кривой при равных мощностях помех на каждом входе адаптивных фильтров, поэтому важно не допускать таких соотношений. Следовательно, сначала необходимо разделить помехи, а только потом подать на опорные входы компенсатора.

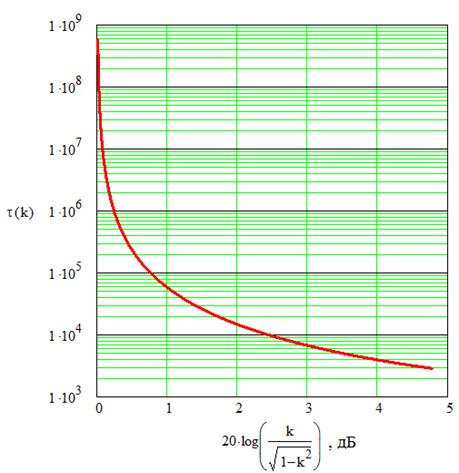
Рис. 2. Зависимость максимального значения постоянной времени обучающей кривой от отношения мощностей помех в каналах (α=0.001).

Многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах

В этой связи предлагается структурная схема компенсатора помех на основе многоканальной адаптивной обработки с предварительным слепым разделением[1]помех в опорном канале. От традиционной многоканальной компенсации схема отличается тем, что сначала помехи с помощью соответствующего алгоритма разделяются, а затем раздельно подаются на отдельный вход каждого опорного канала. Таким образом, можно иметь гарантированную и быструю сходимость к оптимальным весовым коэффициентам.

Выбор слепых алгоритмов для разделения помех обусловлен их работоспособностью, когда отсутствует информация о параметрах помех за исключением отдельных априорных предположений (о принадлежности к классу распределений, о различии статистических характеристик помех, о некоторых корреляционных свойствах помех и т. п.). Еще одним их достоинством является возможность применения алгоритма слепого разделения, в котором количество приемных датчиков может быть меньше количества помех. Например, таковым является алгоритм DUET.

Таким образом, структурная схема, реализующая компенсационный метод на основе многоканальной адаптивной обработки сигналов и слепого разделения помех в опорном канале, может быть представлена следующим образом (рис. 3).

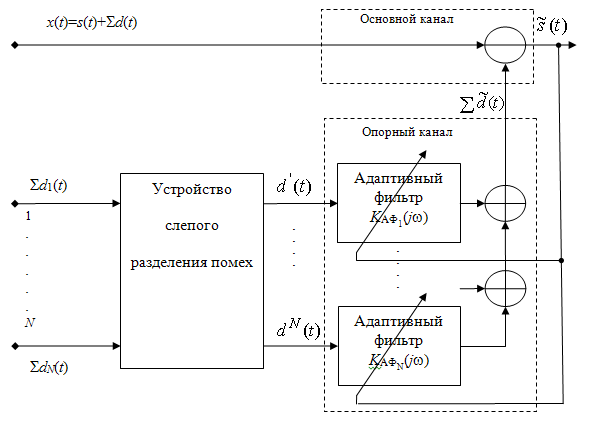
Рис. 3. Структурная схема, реализующая компенсационный метод на основе многоканальной адаптивной обработки сигналов и слепого разделения помех в опорном канале

На входы устройства разделения помех подаются сигналы с N датчиков, в которых действуют смеси помех Σd_i(t). На выходе устройства разделения оценки помех подаются на входы опорных каналов. Адаптивные фильтры работают независимо, по единому выходному сигналу. По окончании адаптации на выходе структурной схемы формируется оценка полезного сигнала .

Адаптивная компенсация помех с использованием модифицированного алгоритма слепого разделения Жуттена-Эро

Наиболее простым для реализации является модифицированный алгоритм слепого разделения сигналов Жуттена-Эро[2] [5]. Вводится предположение, что разделяемые процессы s₁…s_n независимые. В качестве устройства разделения используется искусственная нейронная сеть (ИНС) с обратными связями (рис. 4).

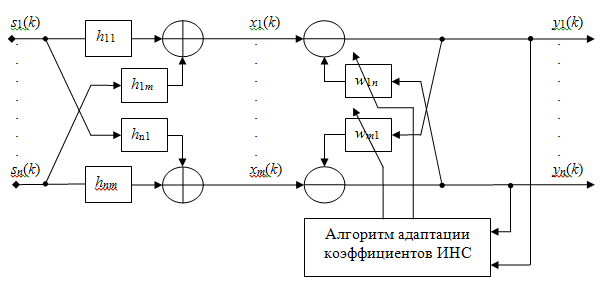
Рис. 4. Нейронная сеть для разделения сигналов

Алгоритм адаптации весовых коэффициентов ИНС выражается:

, (15)

где Λ — единичная матрица; f(y) и g(y) — нечетные функции активации (например, можно использовать нечетные функции tanh(y) и y³); m_инс — параметр адаптации нейронной сети.

Диагональные коэффициенты нейронной сети w_ii обеспечивают самонормализацию дисперсий выходных сигналов, что улучшает характеристики сети, даже если смешивающая матрица является плохо обусловленной [6].

Алгоритм (15) представлен в среде Mathcad на рис. 5. Для разделения моделируется аддитивная смесь объемом выборки N из двух процессов — гауссова широкополосного шума и гауссово-марковского процесса с относительной полосой α=0.001, которая принимается двумя датчиками.

Рис. 5. Программная реализация модифицированного алгоритма Жуттена-Эро в среде Mathcad

Качество разделения контролировалось по отношению мощностей сигналов в каналах после их разделения:

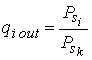, (16)

где — мощность i-го отделяемого сигнала; — мощность k-го сигнала.

Результаты компьютерного моделирования алгоритма (15) отображены в таблице 1 (при µ_инс=10^-3).

Таблица 1.

q_in, дБ	0.5	1	3
q_{1 out}, дБ	12.3	12.4	14.7
q_{2 out}, дБ	11.3	11.9	13.1

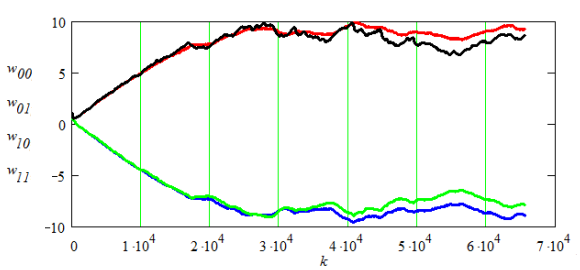
Рис. 6. Зависимость коэффициентов нейронной сети от времени при отношении мощностей в каналах 0.5 дБ и µ_инс=10^-3 (w₀₀ – красная; w₀₁– синяя; w₁₀– зеленая; w₁₁ – черная)

Время сходимости, рассчитанное по формуле (14), без предварительного разделения помех и при отношении мощностей в каналах 0.5 дБ составляет порядка 220000 отсчетов. При этом с использованием алгоритма слепого разделения помех (15) время сходимости коэффициентов нейронной сети (по рисунку 6) составит не более 30000 отсчетов, а время сходимости градиентного алгоритма наименьших квадратов с учетом табличных значений отношения мощности помех в каналах (таблица 1) при 11.3 дБ — не более 800 (по ф. 14). Соответственно суммарное время сходимости получается путем сложения времени сходимости коэффициентов нейронной сети и времени сходимости алгоритма наименьших квадратов.

Таким образом, выигрыш по скорости сходимости от предварительного слепого разделения помех в каналах составляет:

(17)

Компьютерное моделирование работы многоканального адаптивного компенсатора помех со слепым разделением помех

Проведем компьютерное моделирование работы многоканального адаптивного компенсатора помех с использованием модифицированного алгоритма Жуттена-Эро слепого разделения помех в каналах. Полезный сигнал — гауссово-марковский процесс с относительной полосой α=0.1. Помехи — широкополосный шум с распределением Рэлея и узкополосный гауссово-марковский процесс с относительной полосой α=0.001. Параметры и результаты моделирования изображены в таблице 2 и рис. 7.

Таблица 2.

*Параметр*	*Значение*
Число весовых коэффициентов адаптивного фильтра в каждом канале	2
Коэффициент адаптации АКП	0,01
Параметр адаптации нейронной сети	0,001
Алгоритм адаптации АКП	метод наименьших квадратов
Входное отношение сигнал-помеха, дБ	-15,5
Выигрыш в отношении сигнал-помеха на выходе АКП, дБ	24
Отношение мощностей помех в каналах до разделения q_in, дБ	0,5
Отношение мощностей шума к гауссово-марковскому процессу в 1 канале после разделения q_1out, дБ	23,2
Отношение мощностей гауссово-марковского процесса к шуму во 2 канале после разделения q_2out, дБ	14,3

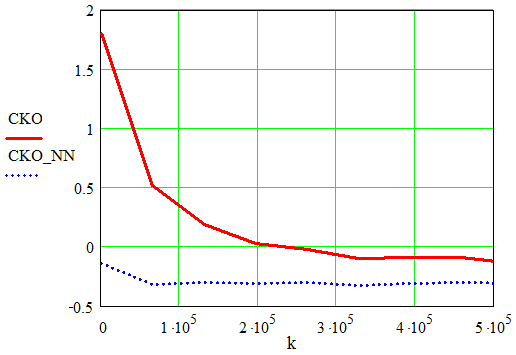
Рис. 7. Изменение дисперсии ошибки фильтрации во времени без предварительного разделения помех (СKO) и с предварительным разделением помех (CKO_NN) при отношении мощностей в каналах 0,5 дБ

Выигрыш в сходимости при использовании алгоритма слепого разделения помех в опорном канале составляет не менее 6 раз.

Проведем аналогичный эксперимент с аддитивной смесью из двух узкополосных помех и одной квазигармонической помехи, при этом выделяемый сигнал — М-последовательность. Для приближения работы адаптивного компенсатора к реальным условиям помехи в опорном канале проходят через фильтры, имитирующие особенности радиоканала, с импульсными характеристиками, изображенными на рис. 8. Параметры моделирования отображены в таблице 3, результаты моделирования — в таблицах 4, 5 и рис. 9.

Качество выделения сигнала компенсатором контролировалось через зависимость вероятности ошибки приема отсчета (p_ош) и выигрыша по отношению сигнал-помеха на выходе АКП (G) от отношения сигнал-помеха на входе устройства разделения (η).

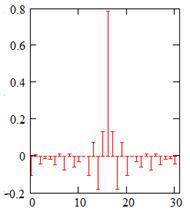
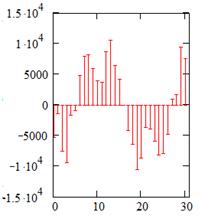
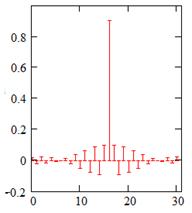
а) б) в)

Рис. 8. Импульсные характеристики фильтров а) для квазигармонической помехи, б) для первой узкополосной помехи, в) для второй узкополосной помехи

Таблица 3.

*Параметр*	*Значение*
Период М-последовательности	2⁵-1
Формирующий полином М-последовательности
Центральная частота и ширина полоса 1 узкополосной помехи	300; 0,001
Центральная частота и ширина полоса 1 узкополосной помехи	500; 0,001
Центральная частота квазигармонического процесса	100
Число весовых коэффициентов адаптивного фильтра	256
Коэффициент адаптации АКП	0,01
Алгоритм адаптации АКП	метод наименьших квадратов
Параметр адаптации ИНС	0,0001
Общий объем выборки	589824
Объем выборки для оценки р_ош	32768

Таблица 4.

Отношение мощностей 1 (2,3) помехи к остальным помехам в 1 (2,3) канале до разделения q_in, дБ	0
Отношение мощностей квазигармонической помехи к остальным помехам в 1 канале после разделения q_{1 out}, дБ	26,0
Отношение мощностей 1 узкополосной помехи к остальным помехам во 2 канале после разделения q_{2 out}, дБ	16,0
Отношение мощностей 2 узкополосной помехи к остальным помехам в 3 канале после разделения q_{3 out}, дБ	20,3

Таблица 5.

η, дБ		-18.8	-15.1	-12.7	-9.3	-6.6	-4.8	-1.45	1.2
Без разделения помех	p_ош	0.38	0.32	0.27	0.19	0.11	0.07	0.03	0.01
Без разделения помех	G, дБ	8.7	8.4	8.4	8.1	8.1	8.0	7.3	6.6
С разделением помех	p_ош	0.25	0.14	0.1	0.04	0.02	0.01	0.008	0.007
С разделением помех	G, дБ	15.4	15.7	15.2	14.6	13.8	13.7	11.3	9.7

Худшие результаты в таблице 5 дает адаптивный компенсатор без предварительного разделения помех в каналах, что объясняется его более медленной сходимостью и незавершенностью процесса адаптации АКП за весь обрабатываемый объем выборки.

Слепых алгоритмов подавления помех существует большое множество и в случае аддитивного смешивания помех возможно применение достаточно быстрых алгоритмов, время сходимости которых значительно меньше, чем сходимость градиентных алгоритмов при плохой обусловленности корреляционной матрицы входного сигнала адаптивного фильтра. Например, при разделении речевых сигналов скорость сходимости алгоритма ICA составляет не более 500 итераций [7], а при разделении квазигармонических сигналов натуральным градиентным алгоритмом — не более 200 итераций [8]. Поэтому используя предварительное слепое разделение помех в каналах можно в несколько раз снизить время сходимости алгоритма наименьших квадратов при адаптации весовых коэффициентов фильтра.

а)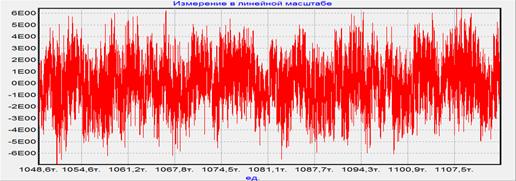

б)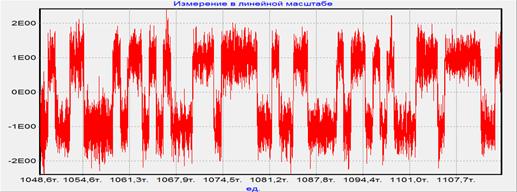

Рис. 9. Аддитивная смесь полезного сигнала и помех на входе АКП (а), выходной сигнал АКП с предварительным разделением помех (б) при отношении сигнал-помеха h=-4.8 дБ

Выводы

1.     Синтезирован многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах, позволяющий при использовании алгоритма адаптации МНК повысить скорость сходимости при плохой обусловленности корреляционной матрицы помех.

2.     Доказано, что при использовании модифицированного алгоритма слепого разделения Жуттена-Эро можно увеличить скорость сходимости в 6-7 раз.

3.     Продемонстрировано, что при выделении М-последовательности многоканальным адаптивным компенсатором со слепым разделением на фоне помех с отношением сигнал-помеха минус 15 дБ и заданным в эксперименте объемом выборки 589824 отсчетов можно снизить вероятность ошибки более чем в 2 раза по сравнению с многоканальным компенсатором Уидроу.

Литература

1. Венскаускас К.К. Компенсация помех в судовых радиотехнических системах. – Л. : Судостроение, 1989. – 264 с., ил.

2. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Пер. с англ. – М. : Радио и связь, 1989. – 440с.

3. Шарый С.П. Курс вычислительных методов. – Новосибирск : Институт вычислительных технологий СО РАН, 2013. – 497 с.

4. Джиган В.И. Адаптивная фильтрация: теория и алгоритмы. – Москва : Техносфера, 2013. – 528 с.

5. C. Jutten and J. Herault. Blind separation of sources. Part I. An adaptive algorithm based on neuromimetic architecture. Signal Processing, 24(1) : 1–10, July 1991.

6. A. Cichocki and S. Amari. Adaptive blind signal and image processing: learning algorithms and applications, John Wiley & Sons (2002).

7. H. Saruwatari T. Kawamura K. Shikano. Fast-convergence algorithm for ICA-based blind source separation using array signals processing Proceedings of the 11th IEEE Signal Processing Workshop on Statistical Signal Processing. 2001 pp.464-467.

8. M. G. Jafari, S. R. Alty, and J. A. Chambers, “New natural gradient algorithm for cyclostationary sources” IEE Proc.-Vision Image and Signal Processing, February 2004, vol. 151(1), pp. 62–68.