Повышение эффективности обработки и формирования сигналов в РЛС с СДЦ методами рандомизации

 

Ю. Н. Горбунов

ИРЭ им. В.А. Котельникова РАН, Фрязинский филиал

Статья получена 29 сентября 2014 г.

Аннотация. В статье анализируется развитие стохастических когерентно-импульсных РЛС с СДЦ: от первого внедрения в них режимов псевдослучайной вобуляции частоты повторения зондирующих импульсов для устранения эффекта «слепых скоростей» до рандомизации приема сигналов, реализации принципов стохастического принятия решений, стохастического «обеления» пассивных и активных помех и в перспективе - полномасштабного применения шумовой СШП радиолокации, реализующей форму функции неопределенности, удовлетворяющей требованию круговой симметрии.

Ключевые слова: когерентно – импульсные РЛС, селекция движущихся целей (СДЦ), рандомизация, шумовая радиолокация.

Abstract. The article analyzes the development of stochastic coherent-pulse radar MTI: from the first introduction of these modes wobble pseudorandom pulse repetition frequency to eliminate the effect of the "blind speed" before randomization to receive signals, implementation of the principles of the stochastic decision-stochastic "whitewashing" of passive and active interference and in the future - the full implementation of the noise UWB radar implements a form of ambiguity function satisfies the requirements of the circular symmetry.

Keywords: coherent - Pulse radar, moving target indication (MTI), randomization, noise radar.

 

Введение и постановка задачи

Исследования на тему «современная радиолокация» безусловно в первую очередь идут по пути выбора вида зондирующих сигналов и совершенствования методов и средств цифровой, в общем случае пространственно-временной (ПВ, «the spatial time processing» SP) обработки эхо-сигналов в когерентно-импульсных РЛС с системой СДЦ (класс РЛС «coherent pulsed radar» с системой СДЦ  «system moving target indication»  MTI).

Актуальность исследований заключается во внедрении в технику обработки и формирования РЛ сигналов новых цифровых технологий, поднимающих радиолокацию на новый современный уровень. Это:

- использование когерентно-импульсных зондирующих сигналов (последовательностей) со случайными параметрами (периодом повторения, несущей частоты, фазой квантования и т. д.), прирост «стохастичности» в стремлении реализации преимуществ сверхширокополосной (СШП) радиолокации по сравнению с традиционной радиолокацией с детерминированными сигналами;

- реализация распределённой системы пространственно-временной (ПВ) обработки  в когерентно-импульсных. РЛС с СДЦ и ФАР, осуществляющей доплеровско - угловую селекцию целей на фоне мощных активных А и пассивных П помех с помощью адаптации приема и подавления помех с помощью формирования «нулей» в АЧХ системы СДЦ и ДНА ФАР РЛС;

- реализация адаптивного приёма и формирования сигналов в условиях произвольных помех и большой неопределенности в выборе параметров сигнала и способов их обработки;

- повышенная скрытность работы РЛС с реализацией сниженного уровня заметности защищаемого объекта.

Цифровой обработке (ЦО), несмотря на известные преимущества, присущи недостатки: наличие  эффектов стробоскопического характера («слепые фазы», «слепые направления», «слепые скорости»), нелинейностей амплитудных характеристик типа  «зона нечувствительности», «люфт», «жёсткое ограничение», наличие шумов квантования,  округления  и т.п., которые обычными способами, вытекающими из классической теории ПВ обнаружения учесть не удается.

При устранении указанных недостатков в авиационных и космических РЛС для получения гарантированных решений необходимо учитывать не только ограничения по определению области предсказания в выборе и параметров сигналов, но и ресурсные ограничения: разрядность, частоты квантования, размеры окон ПВ выборок, размеры областей предсказания и многообразие способов устранения априорной неопределенности.

В работах [1-3] и других российских и зарубежных авторов исследованы вопросы анализа и синтеза цифровых устройств и алгоритмов обработки РЛ-сигналов, однако специальные разделы, относящиеся к устранению вышеуказанных недостатков исследованы недостаточно.

 На Рис. 1, приведены примеры изображений ЛА, летящего на «оптимальной скорости» при 16- разрядной обработке и бинарном квантовании при различных отношениях сигнал/шум , видно, что разрядность обработки выбрана нерационально и хорошее качество выделения сигнала  может быть достигнуто и при бинарном квантовании  с рандомизацией порога на уровне 0,5 по напряжению [4].

                      

= 20 дБ

          

= 0 дБ                                                = -10 дБ

 

Рис. 1 Обработанные изображения ЛА с рандомизацией порога (слева) и без рандомизации (справа)

В то же время, если попытаться использовать весь ресурс 16- разрядной обработки и слабый сигнал «обрабатывать правильно», то при полете цели на «слепой» скорости она все же полностью исчезнет с экрана радара.

Рандомизация обработки РЛ сигналов

Малоразрядной цифровой обработке в условиях вышеупомянутых ресурсных ограничений посвящена работа [4]. Эти ограничения проявляется в современных авиационных и космимческих РЛС, где система ЦО, в особенности для РЛС с ФАР представляет собой достаточно разветвленную сеть (многопроцессорную, многоканальную).

 При параллельной обработке информации (на регистровом и топологическом уровнях, в параллельных интерфейсах) разрядность информационных потоков радиолокационных данных напрямую определяет техническую сложность построения аппаратуры (фазовращатели, умножители, процессоры, нормализаторы задержек). Поэтому разрядность РЛ данных, частоты дискретизации, размеры окон ПВ-выборок должны быть минимальными.

В [4] приведен пример реализации принципа рандомизации на примере стохастического 2-х битового АЦП, в котором использован способ «зашумления» измеряемого сигнала симметричным шумом , где обнаружены «узлы» и «пучности» дисперсии шума квантования вокруг линии «идеального» (многоразрядного) АЦП. Дисперсия уменьшается как 1/N с ростом числа N обрабатываемых отсчетов при независимых отсчетах.

Следует отметить, что в рассмотренном примере использовался двухбитовый АЦП. Можно привести еще один пример, когда для установления факта пересечения подбрасываемой иглы на параллельные линии в методе Монте-Карло использовался 1 бит, в тоже время частота пересечений линий в серии N испытаний была связана с числом p, которое, как известно, является иррациональным числом, а следовательно представления кодом с бесконечной разрядностью [5].

Необходимо отыскать резервы повышения эффективности ЦО при использовании РЛ данных с бинарными признаками (малоразрядных, бинарно-знаковых, булевых и т. п.).

Для того, чтобы обнаружить цель, необходимо ослабить действие стробоскопического эффекта, т.е. исключить регулярность квантования в медленном (по Доплеру) времени аналогично рандомизации по амплитуде при рандомизированном квантовании, т.е. хаотически изменять период повторения зондирующих импульсов.   

Таким образом, актуальной задачей для получения гарантированных решений, повышающих эффективность ЦО ПВ сигналов, её основных процедур (обнаружения, оценивания параметров, а в общем случае фильтрации по обычным и пространственным частотам - угловым направлениям, фильтрации траекторий) в условиях неопределенности в выборе параметров и ресурсных ограничений является отыскание адекватных решений.

Для этих случаев автором в течение многих лет была подробно исследована совокупность технических приёмов (методов, способов) уменьшения влияния стробоскопических и интерференционных эффектов, других эффектов дискретизации и квантования, что связано с целенаправленным использованием преимуществ рандомизированной обработки.

Термин randome (случайный) предполагает искусственное введение случайностей (случайные пороги, случайные аддитивные учитываемые добавки, случайные весовые коэффициенты и др.) в процедуру обеления шумов квантования, обусловленных дискретизацией. Процедуры подобного типа известны в литературе, однако систематизированное и научное изложение данного вопроса на сегодня отсутствует. На основе такого подхода на сегодня автором создан целый ряд конкретных устройств, реализирующих различные способы обеления («рандомизации», «стохастической линеаризации», «накачки», «вобуляции» и т.п.).

Предложенный метод, базирующийся на идейной основе метода Монте-Карло, в рамках рассматриваемого подхода был применен при построении различных технических устройств.

Вобуляция частоты повторения зондирующих импульсов в РЛС

В ранее закрытой работе [6] впервые было рассмотрено стохастическое квантование в «медленном времени», как средство устранения эффекта «слепых» скоростей РЛС в режиме СДЦ .

Периодически повторяющиеся «узлы» и «пучности» дисперсии шума квантования вокруг линии «идеального» (многоразрядного) АЦП эквивалентны периодически повторяющимися «слепым» и «оптимальным» скоростям, когда радиальная скорость цели , где , либо , - длина волны, Т- период повторения зондирующих импульсов РЛС.

Фазовое состояние РЛС, задаваемое выбранным значением периода повторения зондирующих импульсов , i = 1, 2, … N, где N – число импульсов в пачке, для каждого  определяет регулярное на оси скоростей положение «слепых» и «оптимальных» скоростей и соответствующих им доплеровских частот. Желательно, чтобы  соответствовало «оптимальной» скорости, однако при неизвестной скорости цели и в условиях ограничений на диапазон перестройки периода повторения обеспечить это невозможно.

В результате решения вариационной задачи в условиях неизвестной скорости была проведена статистическая оптимизация закона вобуляции частоты  повторения (ВЧП)   в    когерентно-импульсной РЛС с СДЦ.

С математической точки зрения указанная задача по своему содержанию сводилась к решению классической вариационной задачи отыскания минимума определенного интеграла (интеграла Стилтьеса), задаваемого функцией N переменных , удовлетворяющей по каждой переменной граничным условиям и условиям нормировки. Этот интеграл для распределения доплеровских скоростей F(V) являлся функционалом качества:

,

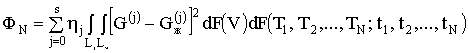где  - N-мерное множество решений,  - варьируемые и желаемые скоростные характеристики системы СДЦ и их j -е производные.

Совместная оптимизация алгоритма вобуляции достигалась тем, что значения периодов зондирования  выбирались из условия получения требуемой случайной модуляции с учетом корреляционных свойств формируемой последовательности .

В начале семидесятых годов в системах синхронизации РЛС для образования случайных кодов ВЧП зондирующих импульсов успешно использовались генераторы шума на основе полупроводниковых элементов, таких как диоды, транзисторы.

Первый цифровой ВЧП [7], имеющий повышенную надежность, проявляющуюся в стабильности      воспроизведения    вероятностных характеристик потока случайных импульсов  запуска РЛС при изменении климатических условий, был внедрен в разработки РЛС в 1972 г.

Для вектора наблюдения , сигнала цели  отношение правдоподобия, после логарифмирования и упрощения для гипотез,  записывается в виде [8]:

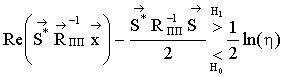                        ,                                        (1)

 где  - корреляционная матрица гауссовой П  с нулевым средним неизвестной мощности, * - знак комплексного сопряжения, η – порог.

Первое слагаемое в формуле (1) является отбеливающим режекторным фильтром (РФ), а второе - согласованным фильтром. Разность сравнивается с модифицированным порогом.

Известно, что согласованный фильтр максимизирует отношение в условиях равномерного шума, а отбеливающий фильтр декоррелирует цветной шум, делая его белым, при этом, порядок выполнения вышеупомянутых операций, может быть произвольным.

Величина есть отношение , увеличение которого способствует разделению функции плотности распределения вероятностей принимаемой сигнально-помеховой смеси для гипотез  и .

Однако, поскольку АП коррелированна по пространству,  схема обработки для угла прихода АП формирует ноль характеристики пространственного фильтра. Далее осуществляется пространственная согласованная фильтрация, которая в целом максимизирует . Таким образом, система ПВ обработки формирует «нули» на оси доплеровских (для ПП) и пространственных (для АП) частот.

Пассивная помеха ПП демонстрирует двухкоординатную корреляцию по углу и времени (Доплеру), что сегодня оформлено построением современной теории ПВ обработки [8]). Эта теория легко развивается на случай N импульсов в пачке и MхL пространственных каналов по азимуту и углу места с использованием ПВ «окна наблюдений» размером NхMхL.

Пространственно-временные отличия сигналов цели и помех увеличивают соответствующие степени свободы взвешивания статистики наблюдения с помощью вектора пространственно-временных коэффициентов . Взвешивание отчетов с помощью этого вектора  осуществляется с целью реализации принципа согласованной фильтрации адаптивно в реальном времени.

Помехи от местных предметов коррелированны по пространству и времени, в то время как преднамеренная помеха коррелированна по углу и однозначно определена ситуационной задачей взаимного положения цели и постановщика помех.

ПВ обработка сигналов включает в себя  адаптивную настройку весовых коэффициентов , где N, M, L – номера временных и пространственных (по азимуту  и по углу места ) отсчетов, а N, M, L – размеры временного (N) и пространственного (M×L) окна, в попытке достичь максимального значения  и, следовательно, вероятности правильного обнаружения .

При этом используется понятие «сигнал/(помеха+шум+шум дискретизации и квантования)» , которое учитывает шумы квантования и (в более общем случае) другие эффекты дискретизации и квантования, присущие дискретной и цифровой обработке сигналов. Детализацию отношения  целесообразно проводить по Брэннану – Риду [3].

Стохастическая интерполяция дальности

Возможность повышения инструментальных возможностей рандомизации применительно к задаче уточнения положения центра тяжести сигнала по пачке N импульсов РЛС в режиме обнаружения [9] ( см. Рис. 2) при бинарном квантовании дальности внутри элемента разрешения по дальности Δ впервые доказана в [10] и далее подробно исследована в [11, 12].

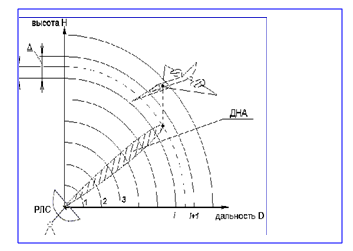
Рис.2. Интерполяция дальности D

Очень часто из-за неопределенности положения центра тяжести сигнала внутри элемента разрешения Δ энергия пачки импульсов распределяется между соседними элементами разрешения, что приводит к энергетическим потерям полезного сигнала и необходимости «сшивания пакета».  

В [11,12] приведены результаты исследований по разделу «Адаптация приёма ПВ сигналов путём организации многоэтапных рекурсивных процедур для оценивания параметров (компонент) вектора измеряемых параметров», где на примере измерения дальности обосновывается возможность изменять условия измерений, сформулированная как адаптация приема ПВ сигналов.

Процесс измерений параметров повторяющегося сигнала организован по принципу «удлиняющейся серии». В результате обзора методов отмечена близость предлагаемого способа к «урновой схеме Пойя» и в меньшей степени сходство с классической процедурой Вальда.

Процесс оценивания может быть организован последовательно по серии (пачке) из N временных, и М, L пространственных отсчетов в апертуре ФАР, в результате чего снижаются требования к разрядности квантователей и открываются возможности применения рандомизированной обработки по всем координатам. Размеры временных и пространственных окон по времени (N), азимуту (M), и углу места (L) выступают как естественный ресурс доплеровской и пространственной селекции. «Обеление» П и А помех осуществляется одновременно с «обелением» шумов квантования.

 Задача интерполяции дальности, скорости, азимута и угла места – сводится к задаче измерения уточняющей интерполирующей добавки  и связанной с ней вероятностью p=/Δ, где - ошибка квантования, подлежащая оценке; - шаг квантования.

Таким образом, речь идет об измерении  методом статистических испытаний с использованием «грубой» (булевой) статистики . Разумно введенная отрицательная корреляция между элементами всего вектора-выборки размером NxМxL может приводить к отрицательным членам с ковариациями в формуле для СКО и уменьшить её по сравнению с обычным случаем. 

Стохастическое обнаружение

В классической теории решений [13] проектировщик системы не может управлять сигналом на входе: операция передачи  задаётся априори, все сигналы заданы наперёд вместе с вероятностями наступления каждого из них, и проектировщик не может изменять эти данные, т. е. заданы распределения принимаемых сигналов F_N,M,L(/0) и F_N,M,L(/), где и  – N,M,L - мерные векторы пространства наблюдений и сигналов.

В работе [4,14] сформулирован подкласс задач, отличающихся тем, что в формировании пространства наблюдений принимает участие «Наблюдатель», который может рандомизировать процесс приема сигналов путем использования случайных порогов (порогового «джиттера»).

В таких обнаружителях пространство наблюдений разбивается не на два (как это принято в классической теории), а на три множества с образованием промежуточной зоны, в которой вероятность принятия решения назначается Наблюдателем ).

Нормировка распределений достигается использованием статистики сравнений Манна-Уитни [15] (булевой или ранговой статистики), в результате чего процедуры обнаружения приобретают робастные (непараметрические) свойства, а вероятностные характеристики эффективности РЛС становятся инвариантными к распределению шума.

Путём рандомизации пороговых уровней в дискретных точках вероятностей правильного обнаружения и ложной тревоги становится возможным линеаризовать рабочую характеристику  радара.

На примере сглаживания траекторных измерений сближающихся объектов в задаче прогнозирования промаха был рассмотрен метод комбинаторного статистического анализа, в котором задача обнаружения траектории сближающихся объектов («ракета-цель», «георадар-мина») сведена к задаче обнаружения «зашумленной» константы [16].

Для достижения цели в методе предложено сглаживать ошибки измерения на редуцированных плоскостях, при этом снижается порядок эквивалентных «α,β – фильтров» (или фильтров Калмана) при фильтрации достаточно «крутых» гиперболических (по дальности) и обратно-тригонометрических  (по углам) пролётных функций.

Тривиальная модель сближения объектов взаимодействия была взята для упрощения доказательства возможности сглаживания шумов квантования и рандомизирующего шума. Очевидно и то, что не использование обработки «грубых» отчётов на редуцированных плоскостях приводило к увеличению порядка эквивалентных «α, β – фильтров» (или фильтров Калмана) при фильтрации достаточно «крутых» гиперболических (по дальности) и обратно-тригонометрических  (по углам) полётных функций сближения объектов.

Цифровая фильтрация

В [17] рассмотрены особенности цифровой фильтрации сигналов по направлению с использованием понятия пространственных частот (см. раздел из «оптики» - «разложение по волновым числам») и процедуры измерения частоты и пеленга в РЛС с ФАР по алгоритмам БПФ.

В результате такой обработки исходная полоса входного сигнала ΔF разбивается на более мелкие частотные интервалы  (< ) («соты», «домены», «фракталы»), в результате чего повышается чувствительность и разрешение «группового» сигнала.

В [17] также приведены результаты аналитических исследований по новой трактовке метода приведения «небелого» шума к «белому» и сформулирован принцип построения стохастических обеляющих фильтров со случайными весовыми коэффициентами (ВК) а_i, в которых с целью сохранения структурно-канонической инвариантности и нормализации задержек по дальности, скорости  и угловым координатам, стабилизации уровня предпорогового шума введена  корреляция ВК при .

В стохастических ЦРФ в виду наличия оператора M₁{·} появляется возможность воспользоваться его интерполирующим действием, т.к. известно, что независимо от того, является ли исходная случайная величина непрерывной или дискретной, ее моменты – являются непрерывными величинами.

В работе [4] рассмотрены вопросы построения стохастических ФАР, при этом отмечена неожиданная взаимосвязь с заметностью антенн, что весьма важно для интегрированных бортовых РЛК. Показано, что контролируемый джиттер весовых коэффициентов ПВ-фильтров (ФАР) уменьшает фоновую составляющую КНД, обусловленную шумами квантования цифровой системы даграммообразования.

В [4] также приведены результаты аналитических исследований  цифровой системы СДЦ с идеальным (жестким) ограничением сигнала на входе и рандомизацией алгоритма обработки N-импульсной пачки импульсов после бинарно-знакового АЦП.

Стохастическая дискретизация пространства

Проведены аналитические исследования вопросов восстановления сигнальных полей, дискретизированных по времени и пространству с применением стохастических шкал квантования [4, 18], сформулированы варианты теорем отсчётов, дающие возможность восстанавливать дискретизированные по времени и пространству сигнальные поля в связи с необходимостью их фильтрации по обычным и пространственным частотам (угловым направлениям).

В [4] приведены результаты моделирования частотомеров и пеленгаторов для задач РТР-РЭП и радиолокации. В качестве метода измерения моделирования взят моноимпульсный метод, а в качестве конкретного способа выбран способ «фрактальной суммарно-разностной обработки», согласно которому на оси обычных  или пространственных  частот выявляется пара смежных каналов i, i+1 и образуются суммарные  и разностные  каналы. В рабочей зоне по частоте и угловым координатам образуется «веер лучей» каналов временного или пространственного БПФ.

Моделирование квазилинейных трактов ПВ обработки сигналов в условиях искусственно загрубленного квантования квадратурных компонент входного сигнала (использована предельно «грубая» статистика μ_i=±1) и доказало линеаризующее действие шумового напряжения, рандомизирующего процесс квантования.

В ходе моделирования применялся амплитудный, временной (фазовый) «джиттер» (дрожание шкал квантования), а также «джиттер» ВК стохастического ЦФ (временного и диаграммообразующего).

Многочастотная и шумовая радиолокация

Наибольшее распространение в многочастотной радиолокации получили сигналы с линейным законом изменения частоты сигнала от импульса к импульсу, т.е. сигналы с линейной БПЧ. Сигнал с линейной БПЧ по существу является последовательностью узкополосных импульсов с изменяющейся частотой, который в определенной степени аналогичен одиночному импульсу с внутриимпульсной линейной частотной модуляцией (ЛЧМ), который трансформирован в пачку N импульсов, значения амплитуд и фаз эхо-сигналов которых записываются в память ЭВМ. Далее в электронном виде формируется многочастотно-временная матрица рассеяния (МВМР), состоящая K из  столбцов и N строк. В столбцах МВМР располагаются комплексные данные на N различных частотах зондирования, а в строках – данные наблюдений во времени в пределах выбранного интервала синтезирования T_c = NТК [19, 20, 21].

Выбор закона БПЧ в пользу линейного, как и большинства других детерминированных, нельзя считать удачным, т.к. при работе РЛС в условиях АП после проведения противником несложного радиочастотного мониторинга не исключается постановка ответных синхронных помех на частоте закона детерминированной БПЧ. Таким образом, закон БПЧ должен быть случайным.

Перестройка несущей частоты по случайному закону также желательна и по причине придания телу неопределенности формы круговой симметрии, обеспечивающей одинаковые возможности совместного разрешения сигналов как по дальности R, так и по скорости V и борьбы с АП [22].

Однако получить тело неопределенности с нулевыми боковыми лепестками невозможно, т.к. существует известное ограничение, которое не позволяет произвольно менять форму тела неопределенности. По условиям решаемой задачи РЛС подвергается воздействию интенсивных АП, в частности хаотических импульсных помех (ХИП), которые существенно искажают синтезируемое изображение.

Применение на приеме сигналов алгоритмов обработки типа «широкополосное ограничение АП и узкополосная фильтрация» (так называемые системы  ШОУ-фильтр) в этой ситуации является весьма полезным, т.к. бинарно-знаковое квантование сигнала в квадратурах в процессе обработки сигналов (как это показано, например, в [4] ) может быть частично линеаризовано, а жесткое ограничение сигнала на входе придаст свойство непараметричности входной статистике и отнормирует масштаб РЛИ.

Формирование РЛИ

Получение РЛИ цели основывается на способе обработки с помощью преобразования Фурье комплексных огибающих отраженных от объекта сигналов, полученных в процессе многочастотного импульсного зондирования по случайному закону при жестком ограничении квадратурных составляющих входного сигнала на входе.

Комплексная огибающая отраженного от объекта сигнала есть

                                                                                       (2)

 

где А – амплитуда отраженного сигнала,

R - расстояние от РЛС до цели,

λ - длина волны зондирующего сигнала,

φ_отр - скачки фазы, возникающие при отражении от объекта.

Модель исследуемого объекта – совокупность ЛЦР, у которых эффективная площадь рассеяния (ЭПР) при величине λ, изменяется в относительно небольшой полосе  |Δλ|≤0,15λ_ср, где λ_ср – средняя в полосе перестройки длины волны.

Несущая частота РЛС изменяется по случайному закону в диапазоне частот от f_min до  f_max= f_min+ΔF с шагом Δf= ΔF/2^N.

Для получения основных соотношений для получения двумерного РЛИ в координатах x, y, прежде проведем аналогию с теорией антенн.

Известно, что измерение дальности и скорости зависит от характера функции неопределенности в той же мере, в которой угловые измерения зависят от формы диаграммы направленности (ДН) антенны. В нашем случае мы имеем результаты измерения комплексных огибающих (2) на N частотах в K циклах. Совокупность N частотных откликов позволяет построить одномерные РЛИ по дальности x, а K циклов дадут информацию от РЛИ по второй координате y.

Далее будем считать соотношение между числом частот зондирований N, периодом повторения импульсов T и диапазоном перестройки частоты ΔF выбраны таким образом, что измерениями ЭПР за время излучения многочастотной последовательности можно пренебречь, т.е. наиболее узкий лепесток ЭПР цели больше величины изменения ее углового положения. Изменение угла ψ между вектором скорости цели и линии визирования должны достигать 16°, что может быть реализовано естественным образом, либо путем выполнения носителем РЛС специального маневра типа «змейка» или «облет» вокруг объекта.

Комплексные огибающие Φ отраженных сигналов запоминаются в течение времени синтезирования T_c = NТК в угловом секторе ψ и образуют матрицу отсчетов комплексных огибающих размером NK. Далее эта матрица с помощью быстрого двумерного преобразования Фурье преобразуется в матрицу синтезированных откликов. Для каждого элемента матрицы в момент времени t_nm,  измеряется частота f(t_nm) зондирующих импульсов, где n – номер шага перестройки частоты в полосе ΔF, m – номер повторного цикла перестройки.

Результаты измерений комплексных огибающих по аналогии с антенной техникой далее будем рассматривать как результаты измерения комплексной ДН антенны, амплитудно-фазовое распределение поля в апертуре которой подлежит вычислению.

Оператор синтезирования РЛИ выбирается двумерным. Используя понятие пространственных круговых частот [17]

                                                   и

 

запишем выражение для оператора синтезирования  РЛИ, которое представляют собой  двумерное обратное преобразование Фурье

                            .            (3)

 

Измерения Φ производят при дискретных значениях f и ψ, вследствие этого преобразование (3) должно быть представлено в дискретной форме. Для этого переменные интегрирования заменяют номерами элементов некоторой новой двумерной матрицы T

                            ,     ,

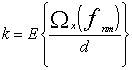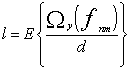где функция целой части числа , d – шаг построения элементов матрицы.

Поскольку диапазон изменения координат  одинаков и равен  где максимальное значение частоты в полосе ΔF ее перестройки, то величина d может быть выбрана одинаковой для .

На практике выбор величины d можно производить исходя из условия недопущения повторного размещения значений  в элементы матрицы T. При этом задают размерность K матрицы T, размещают величины  в элементы матрицы и фиксируют события повторного размещения. Если таковые есть, то размер матрицы увеличивается вдвое и т.д.

Опыт моделирования показывает, что размерность K матрицы T в области переменных  является в 2÷4 раза большим, чем в области переменных f и ψ.

При дискретизации переменных  преобразование в дискретной форме выражается в виде суммы

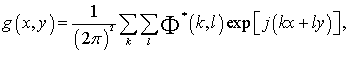                                                (4)

являющейся двумерным дискретным преобразованием Фурье.

Если размерность матрицы Т удовлетворяет условию  , где р – целое число, то реализация (4) выполняется с помощью быстрого двумерного дискретного преобразования Фурье.

Вклад i-го ЛЦР с координатами  и ЭПР  в комплексную огибающую отраженного сигнала на частоте зондирования  в момент времени есть:

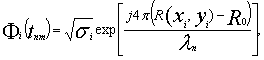                                                              (5)

где  - расстояние от фазового центра антенны РЛС до точки объекта с координатами  в момент времени , - расстояние от РЛС до ЦСЦ.

Это выражение преобразуется к виду

                                                             (6)

где  - координаты i-го ЛЦР.

Результаты моделирования

Задавалась модель объекта в виде совокупности неподвижной относительно связанной системы отсчета ЛЦР.

Зондирующие сигналы РЛС – импульсы с периодом повторения  20 мкс. Несущая частота сигнала изменялась от импульса к импульсу с шагом Δf=3000/511 МГц в полосе частот 3 ГГц от 8,5 до 11,5 ГГц.

Объект вращался по курсу со скоростью 12°/с.

Сектор синтезирования Δψ=16°.

ЛЦР в количестве 30 располагались тремя изолированными группами. В каждой группе имелись ЛЦР с большими,  средними и малыми значениями ЭПР.

Было несколько экспериментов с 2-мя различными группами точек. Зондирование выполнялось на 512 частотах и 128 ракурсах, угол синтезирования 16 град.

1-я группа состояла из 5 точек с ЭПР 5кв.м, 5 точек с ЭПР 0.5кв.м и 39 точек с ЭПР 0.01 кв.м., всего 49 точек. Точки расположены равномерной сеткой 7 X 7 c шагом 1 м. Конкретное расположение точек дано ниже.

2 –я группа отличалась от первой только тем, что была только одна крупная точка, 2 - в 5 раз меньше крупной и 7 – в 50 раз меньше крупной.

ЭПР в этих исходных данных переведена в амплитуду и нормирована к единице.

На рис.3 приведено синтезированное РЛИ  в дБ (относительно максимума равного 1)  без шума приемника, при отсутствии амплитудных и фазовых ошибок и при многоразрядной обработке. Из 39 «маленьких» ЛЦР было распознано 35.

 

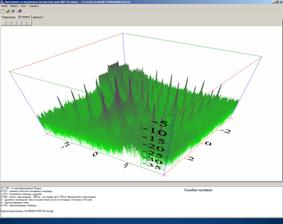
Рис. 3. РЛИ цели из  49 точек.

При ограничении сигнала на входе в условиях мощных АП типа ХИП, превышающих полезный сигнал более чем на 10 дБ, были обнаружены все 10 (5 «больших» и 5 «средних» доминирующих отражателей. Наблюдались эффекты подавления «слабых» ЛЦР «сильными» при малых N  << 512 и К << 128 размерах выборок. Потенциальные потери малоточечных ЛЦР с соезмеримыми ЭПР  составили 1-2 дБ. Хаотические импульсные помехи были подавлены полностью.

Таким образом получение качественных РЛИ целей при работе РЛС  в условиях мощных активных хаотических импульсных помех представляет сложную техническую задачу. Тем не менее, синтез двумерных РЛИ целей с ограниченным числом равновеликих доминирующих отражателей методом многочастотной радиолокации, вполне реален. Точки с малыми значениями ЭПР подавляются. Алгоритмы обработки сигналов предполагают использование ограничения активных помех в квадратурах с последующей рандомизацией бинарно-знаковой статистики при формировании РЛИ. Основой синтеза РЛИ является большая  совокупность элементов многочастотно-временной матрицы рассеяния, состоящей из отсчетов амплитуд и фаз комплексной огибающей на всем интервале синтезирования.   Потери потенциальной помехоустойчивости обнаружения и измерения координат ЛЦР составят 1-2 дБ.

Заключение:

1. Проведен научно-аналитический обзор методов и средств рандомизации процедур цифровой обработки и формирования сигналов в когерентно-импульсных РЛС с системами СДЦ, разрешающих неопределенность по априорной информации о координатном положении и   движении цели в условиях аппаратных и ресурсных ограничений по: разрядности АЦП и ЦФ, частотам квантования при стохастической интерполяции, размерам окон ПВ выборок, размерам областей предсказания и многообразию способов устранения неопределенности.

2. Обоснована необходимость введения рандомизирующих хаотических воздействий на параметры обрабатываемых сигналов с целью расширения полос шумов квантования (для  последующего сглаживания), уменьшения влияния стробоскопических эффектов дискретизации, стохастческой линеаризации нелинейностей с целью минимизации потерь обнаружения слабых сигналов движущихся целей на фоне мощных пассивных и активных помех.

3. Выявлена тенденция системно-функционального «прироста стохастичности» в параметры синтезируемых зондирующих сигналов и в параметры соответствующих устройств цифровой обработки в направлении снижении аппаратных и ресурсных ограничений в реализации современных РЛС авиационного, космического и наземного (морского) базирования с разветвленной сетью дискретной и цифровой пространственно-временной обработки.

4. В результате моделирования процедур СШП радиолокации с ПНЧ при построении объемного РПИ цели на несущей частоте 10 ГГц с полосой ΔF = 3 ГГц в секторе углов синтезирования Δψ=16° подтверждены основные параметры пространственно-углового сверхразрешения ЛЦР многоточечной цели (коэффициент сжатия спектра до 30 дБ) с сохранением линейных свойств тракта в условиях использования «грубой» непараметрической (робастной) статистики сигналов µ =  в динамическом диапазоне более 20 дБ.

5. Подтверждена тенденция развития современной радиолокации по пути более широкого внедрения СШП радиолокации на основе использования зондирующих сигналов в виде  непрерывных хаотических колебаний (шумов) в качестве материальных носителей информации, модуляция параметров эхо-сигналов которых позволит с более высокой эффективностью определить параметры пространственного положения и движения малоразмерных целей на фоне мощных пассивных и активных помех.    

 

Литература

1. Лихарев В.А. Цифровые методы и устройства в радиолокации. - М.: Советское радио, 1973.- 456 с.

2.  Слока В.К. Вопросы обработки радиолокационных сигналов. - М.: Советское радио, 1970. – 256 с.

3.  Brennan L. E., Reed I. S. Quantization Noise in digital Moving Targets Indication Systems. // IEEE Transaction, 1966, vol. AES-2, №6. - р. 655-658.

4.  Горбунов Ю. Н. Цифровая обработка радиолокационных сигналов в условиях использования грубого (малоразрядного) квантования: Монография // Федеральное космическое агентство, ФГУП «ЦНИРТИ им. академика А. И. Берга» - М., 2007. –  87 с.

5. Соболь И.М. Численные методы Монте-Карло.-М.: Наука, 1973.

6.  Горбунов Ю.Н. Теоретическое и экспериментальное исследование вопросов повышения точности автоматического отсчета дальности в импульсных РЛС с цифровой обработкой сигналов.: Кандидатская диссертация. // МАИ. - М.: 1978. – 167 с.

7.  Горбунов Ю.Н., Григоров Н.Р. Вобулятор частоты повторения для РЛС. – Авт. свид. СССР № 80286, 1972.

8. R. Klemm. Space-Time Detection Theory // The material in this publication wa assembled to support a lecture series under the sponsorship of the sensor and lectronicsTechnology Panel (SET) and the Consultant and Exchange Programmer of RTO presented on 23-24 september 2002 in Moscow, Russia.

9.  Lapeyre J.L. Radar a impulsions utilisant l’effet Doppler: influence de l’echantillononag de la distance sur la probabilite de detectetion, interpolation de la distance. // Anales des elecommunications. - 1971, v. 26, № 9/10. - р. 341.

         10. Гайсов В.Г., Горбунов Ю.Н. Двухэтапная процедура измерения временных интервалов методом статистических испытаний с обратной связью. // Автометрия.– СО АН СССР, 1982, № 2.- с.  54 – 60.

         11. Горбунов Ю.Н. Многоэтапная процедура измерения параметров повторяющегося сигнала методом стохастического усреднения цифровых отсчетов. // Автометрия – Сибирское отделение АН СССР, 1985, № 3.  с. 96 – 99.

12. Горбунов Ю.Н. Цифровые методы дальнометрии в импульсных обзорных РЛС.// Автометрия.- 1988, №2.

13. Миддлтон Д. Введение в статистическую теорию связи. // В 2-х томах. – Т. 1,2. Пер.с англ. под ред. Б.Р. Левина. – М., «Сов. Радио» , 1961, 1962.

   14. Горбунов Ю.Н. Цифровые стохастические радары: принятие решений, стохастическое обеление помех, рандомизация измерений параметров, применение. // Труды VIII международной научно-технической конференции «Кибернетика и высокие технологии XXI века». – Воронеж: НПФ «Саквоее», 2007, т.I.-С. 446-455.

15. Томас. Непараметрические методы обнаружения сигналов.// ТИИЭР. - 1970. - т. 58. - №5. – с. 23 – 31.

16. Горбунов Ю.Н., Дружко С.Н., Гончаров В.А. Квантование временных и пространственных параметров сигнала при прогнозировании промаха сближающихся высокоскоростных объектов в условиях ограничения эненргопотенциала РЛС объекта атаки. //Труды 18-й Международной научно-технической конференции «Радиолокация, навигация и связь», организатор НПФ «Саквоее» при поддержке ОАО Концерн «Созвездие», 2012, т. I. – 8 с.

         17. Горбунов Ю. Н. Цифровые системы СДЦ и их оптимизация: Монография // Государственное образовательное учреждение высшего профессионального образования “Московский государственный институт радиотехники, электроники и автоматики (технический университет)”– М., 2008. – 132 с.

18. Горбунов Ю.Н. Стохастическое временное и пространственное квантование в плоских апертурах фазированных антенных решеток. // Труды X Международной научно-технической конференции «Радиолокация, радионавигация и связь». – Воронеж: Изд. НПФ «Саквоее», 2005, т. III. - с. 1790 - 1798.

        19. Криспин Ж.В. мл., Маффет А.Л.//ТИИЭР. 1965.Т.53.№8.с.960.

        20. Блиновский А.М., Крюков С.В. Способ получения двумерного радиолокационного изображения объекта в большом диапазоне изменения величин эффективных площадей рассеяния локальных центров при многочастотном импульсном зондировании. Патент RV 2372627 с1, кл. G01S13/89.

          21. Горбунов Ю.Н. Особенности формирования радиолокационного изображения цели методом многочастотной радиолокации при работе в условиях активных помех.// Труды 17 Международной научно-технической конференции «Радиолокация, навигация и связь», г.Воронеж, 12-14 апреля 2011 г.- т.3, с.2067-2078.

          22. Горбунов Ю.Н. Особенности работы бортовых авиационных комплексов наблюдения и поиска целей в условиях пассивных и активных помех. // Сборник научных трудов Международной  НТК «Научно-технические проблемы построения систем и комплексов землеобзора, дозора  и управления и комплексов с беспилотными ЛА», проведенной в ОАО «Концерн «Вега», г. Москва, 23 мая 2013 г.