УДК  621.371

Анализ некоторых экспериментальных работ по продольным электромагнитным волнам с позиций классической электромагнитной теории

 

А. Н. Абрамов, В. А. Пермяков, С. В. Пермяков

Национальный исследовательский университет «МЭИ»

 

Статья поступила в редакцию 12 октября 2015 г.

 

Аннотация. Проведен анализ двух экспериментов, опубликованных в работах Monstein, Wesly (1992) и Ацюковского (2011), которые трактуются авторами работ, как наблюдение продольных электромагнитных волн. Показано, что результаты указанных экспериментов могут быть объяснены с позиций классической теории электромагнитных волн без привлечения понятия продольных волн.

Ключевые слова: эксперименты,  продольные электромагнитные волны, классическая теория электромагнитных волн.

Abstract. Two experiments published in the works by Monstein and Wesly (1992) and Atsyukovskii (2011), which are interpreted by the authors as observation of longitudinal electromagnetic waves, are analyzed. It is shown that the results of these experiments can be explained from positions of classical theory of electromagnetic waves without involvement of the concept of longitudinal waves.

Keywords: experiments, longitudinal electromagnetic waves, classical theory of electromagnetic waves.

1. Введение

Для описания реально наблюдаемых процессов распространения электромагнитных волн (ЭМВ) в свободном пространстве  и их  взаимодействия  с материальными  средами в подавляющем большинстве  практических случаев достаточным теоретическим фундаментом является классическая макроскопическая электродинамика, базирующаяся на уравнениях Максвелла (УМ) и простейших  материальных уравнениях, в которых среда описывается такими параметрами, как диэлектрическая  и магнитная проницаемости и проводимости.

В современной электромагнитной теории понятие продольных волн вводится специальными материальными уравнениями для сред с пространственной дисперсией [1,2], развивается также общая теория волн в электромагнитоупругих средах [3].  В ряде работ [4-6] предложены уравнения  обобщенной электродинамики, в которых для описания продольных электромагнитных волн вводятся дополнительные потенциалы, однако эти уравнения являются эвристическими и требуют экспериментального подтверждения.

За последние четверть века появился ряд экспериментальных работ [7-15] (см. также обзор [16] и монографию [17]), которые трактуются,  как  возбуждение электромагнитными полями продольных ЭМВ (ПЭМВ),   обладающих свойствами, существенно отличающими их  от классических ЭМВ.  Характерным недостатком этих публикаций является отсутствие или неполнота трактовки полученных результатов на основе классической электромагнитной теории, под которой в данной статье будем иметь в виду УМ с простейшими материальными уравнениями. Считаем, что согласно принципу «бритвы Оккама»  следует обязательно привлекать  к трактовке   экспериментов  классическую  электродинамику с целью выявления противоречий между теорией и экспериментом. Только в случае обнаружения противоречий  есть  основания привлекать для объяснения экспериментов понятие ПЭМВ. Исходя из этого, проанализируем ниже две публикации по ПЭМВ [11,15] с позиций  классической электромагнитной теории.

 

2. Эксперимент по распространению ПЭМВ между антеннами, расположенными над земной поверхностью

В работе Monstein., Wesley [11]  описан эксперимент по распространению ЭМВ между двумя антеннами  из проводников сферической формы. Возбудителем передающей антенны является коаксиальный кабель, внутренняя жила которого соединена с внутренней оболочкой проводящей сферы, а внешняя оплетка  изолирована от  наружной поверхности сферы. Конструкция приемной антенны аналогична.  Передающая и приемная антенны располагались на фиксированных высотах     относительно земной поверхности. На частоте  433 МГц измерялась зависимость мощности электромагнитной волны, поступившей на приемную антенну, от расстояния между двумя антеннами.   Результаты измерений приведены на рис. 1a) точками, расчет  коэффициента передачи мощности показан – сплошной линией [11]. 

В [11] принята теоретическая модель распространения ПЭМВ, основанная на следующих допущениях.

1. Напряженность электрического поля ПЭМВ выражается через градиент сферически симметричного электрического скалярного потенциала, удовлетворяющего волновому уравнению.

2. Плотность потока мощности ПЭМВ выражается через  напряженность продольного    электрического поля.

3.  Влияние земной поверхности учитывается по принципу зеркального изображения, при этом для согласования с экспериментом расчетные высоты передающей и приемной антенн берутся на  половину длины волны    больше  реальных высот. 

4. Коэффициент отражения ПЭМВ от земной поверхности является подгоночным параметром и подбирается таким образом, чтобы положения двух минимумов, расположенных в интервале дальностей 20…40 м  согласовались наилучшим образом с экспериментом.

         Несмотря на использование подгоночных параметров,  расчетная модель [11] дает  значительные отличия от экспериментальной кривой (рис.1а). Принципиально, что расчетная кривая имеет интерференционный минимум коэффициента передачи на расстоянии  свыше 100 м, отсутствующий в эксперименте. Также теория [11]  не может объяснить  причины резкого убывания экспериментального коэффициента передачи  на больших дистанциях (x>100 м).

 

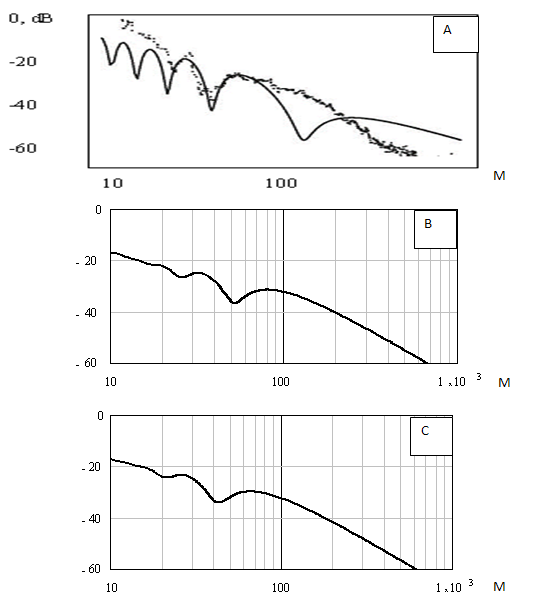
Рис.1.A) Сопоставление экспериментальной зависимости принятой мощности от расстояния между антеннами (точки) с теорией продольных ЭМВ (сплошная линия) [11]. B) Расчет зависимости принятой мощности от расстояния между антеннами по классической теории с учетом отражения электромагнитной волны параллельной поляризации от земной поверхности с  диэлектрической проницаемостью  ε=3 и проводимостью  σ=0,001 См/м. Высота передающей антенны 4м, приемной – 4,4 м. 

C) Аналогичный  расчет по классической теории для высоты передающей антенны 3,6 м, приемной – 4,0 м.

 

         Модель излучения ПЭМВ, принятую  в [11],  следует подвергнуть критике по ряду причин.  Прежде всего обсудим возможность  возбуждения продольной волны скалярным сферически симметричным потенциалом, созданным одиночной сферической проводящей антенной.  Такая возможность ранее обсуждалась в [18] при рассмотрении колебаний плотности заряда, ограниченных сферической поверхностью. Было показано,  что колебания плотности электрического заряда внутри сферической области не меняют распределения электрического поля вне сферы вследствие того, что полный заряд должен оставаться неизменным согласно закону сохранения заряда, то-есть поле вне сферы должно оставаться статическим. Такая ситуация возможна в случае, когда сфера пульсирует и плотность заряда на сфере меняется обратно пропорционально ее площади [19]. Однако для одиночной сферы фиксированного радиуса из закона сохранения заряда следует постоянство плотности заряда на ее поверхности. Поэтому пульсации плотности заряда невозможны. Подобная критика в адрес [11] была дана в [20].

         В применении к эксперименту [11] необходимо учитывать два дополнительных фактора: наличие земной поверхности и реальную асимметрию конструкции антенны с подводящим кабелем. С учетом этих факторов закон сохранения осциллирующего заряда  будет  выполнен в системе в целом.  Поскольку конструкция антенны не является идеально симметричной, на антенне и подводящем кабеле  возникнут несимметричные колебания плотности заряда, создающие классические ЭМВ Е типа, имеющие поперечные компоненты электрического и магнитного поля и продольную компоненту электрического поля [21]. Излучающим эквивалентом такой антенны является система мультиполей, причем из физических соображений наибольший вклад в излучение в горизонтальном направлении должен давать вертикальный электрический диполь.  Кроме того, влияние земли проявится не только в формировании  зеркального изображения излучателя, но и   в искажениях распределений плотностей зарядов на излучателе и его зеркальном изображении. Учет всей совокупности перечисленных факторов достаточно сложен. По этой причине мы рассмотрим простейшую классическую модель экспериментальной  системы [11], представляющую собой два вертикальных диполя, расположенных над плоской земной поверхностью. 

         Классическая модель излучения вертикального диполя над плоской земной поверхностью детально рассмотрена в монографии Фейнберга [22]. Согласно [22]  полное поле вертикального диполя над землей представляет собой сумму трех слагаемых: первичного поля  диполя в свободном пространстве, поля, отраженного от земли и «поверхностной» (в определении [22]) волны. Вкладом «поверхностной» волны можно пренебречь при условии, что высота подъема антенны значительно больше длины электромагнитной волны. Это условие  выполняется в эксперименте.  Оставшаяся часть поля  согласно законам геометрической оптики описывает интерференцию падающего и отраженного от земли полей.   При сформулированных выше условиях для расчета электромагнитного поля можно использовать формулу (27.14) в [22], в которой пренебрежем «поверхностной» волной.

В принятой нами модели также имеются свободные параметры. К ним относятся: дипольный момент вибратора, диэлектрическая проницаемость и проводимость земной поверхности,  высоты подъема вертикальных вибраторов, заменяющих реальные антенны.  Поэтому проведем расчеты, варьируя в разумных пределах свободные параметры. Высоты подъема антенн в соответствии с приведенными в  [11]  данными будем отсчитывать от поверхности земли до центров сфер: высота передающей антенны h₁=4 м,  высота приемной антенны  -   h₂=4,4 м.  

Расчет по формуле Фейнберга (27.14) из [22], учитывающий влияние параметров земли, приведен на рис. 1В  для плоской земной поверхности  с параметрами  ε=3,  σ=0,001 См/м при высотах подъема передающей антенны 4 м и приемной антенны – 4,4 м. Значения параметров земной поверхности выбраны с учетом того, что измерения проводились в городе [11]. При сопоставлении с экспериментом нормирующий множитель   в формуле (27.14) из  [22] выбран из условия совпадения амплитуд расчетных коэффициентов  передачи с амплитудой последнего экспериментального  максимума,  наблюдавшегося при x ≈ 65 м.

Из сравнения расчетов рис. 1B с экспериментом следует, что число расчетных экстремумов коэф. передачи согласуется с   экспериментом в интервале расстояний 20….100 м, в котором экстремальные значения четко выражены. Положения расчетных экстремумов несколько отличаются от экспериментальных. Характер убывания расчетного коэф. передачи рис.1Б на больших дистанциях (x> 100 м  ) ближе к экспериментальному, нежели в расчете  [11].  Последнее объясняется тем, что в модели [11] плотность потока мощности «продольных» ЭМВ убывает обратно пропорционально x², в то время как в нашей модели на больших расстояниях приближение геометрической оптики  переходит в известную формулу Введенского, согласно которой   плотность потока мощности  поперечной ЭМВ убывает обратно пропорционально x⁴ .

Обратим теперь внимание на то, что  вследствие затекания токов по кабелю высоты эквивалентных вертикальных диполей становятся меньше высот расположения сферических антенн. На рис. 1C приведены соответствующие расчеты для высот эквивалентных вибраторов 3,6 м  и 4 м соответственно. Видно, что уменьшение высоты вибраторов приводит к лучшему согласию расчетных положений экстремумов нашей модели с экспериментом.

Выводы по пункту 2:

Использованная в [11]  модель ПЭМВ не согласуется с экспериментом на больших расстояниях (x>100 м), предсказывая ненаблюдаемый минимум коэффициента передачи и меньшую скорость убывания плотности потока энергии с расстоянием.    Только на расстояниях 20…40 м теоретическая модель [11] обеспечивает согласие  с экспериментом благодаря использованию подгоночных параметров, в частности, увеличения высот подъема антенн по сравнению с реальными высотами.

Классическая модель расчета радиолинии между двумя вертикальными вибраторами, расположенными над плоской землей [22], дает качественное и приемлемое количественное согласие с экспериментом [11], в том числе в области измерений, где теория, предложенная в [11], непригодна.  Классическая теория  может быть уточнена при более полной информации о конструкции  антенн и параметров  земной поверхности.

В заключение данного раздела отметим следующее.

·             В работах  [20,23] эксперименты [11] подвергались критике с позиций, сходных с нашими, однако влияние земной поверхности в [23] было учтено нестрого из-за использования  «плазменной» модели проводимости земли, которая менее корректна по сравнению с принятой нами. 

·             В [11]  приведены также результаты эксперимента, доказывающего,  по мнению авторов [11],    существование ПЭМВ  при передаче сигнала между обкладками конденсатора, содержащего фильтр из 9-ти  продольных полуволновых проводящих стрежней.  Такая конструкция  может быть проанализирована численными методами классической электродинамики, но  приведенная в [11] информация недостаточна  для  выполнения этих расчетов. С другой стороны, этот эксперимент доказывает лишь наличие продольной компоненты электрического поля, а не существование чисто продольных ЭМВ.

 

 3. Эксперименты по распространению ПЭМВ между антеннами, расположенными под поверхностью воды

Вопросы беспроводной радиосвязи между объектами, один из которых или более находятся под водой, остаются актуальными многие годы. Не останавливаясь на прикладной стороне подводной радиосвязи, обратимся к публикациям по интересующей нас теме.

Наряду с известными способами подводной связи с помощью классических ЭМВ в ряде работ обсуждались экзотические механизмы связи. В публикациях рекламного плана  1965 – 1967 годов Minto (США)  утверждал, что можно обеспечить подводную связь с помощью так называемых «гидронических» или «плазмонических» волн. В качестве антенн использовались горизонтальные вибраторы с перпендикулярными осям вибраторов  проводящими пластинами на торцах [24]. Связь велась в направлении осей вибраторов.  Утверждалось, что связь может быть обеспечена на частотах до 55 МГц независимо  от глубины погружения антенн. Подобное утверждение вызвало резонное сомнение специалистов, поскольку реально подводная радиосвязь  могла обеспечиваться только при малых глубинах погружения антенн   в режиме возбуждения боковой волны. Эксперименты Minto были критически проанализированы  в [25,26]  в применении к связи между морскими животными с помощью электромагнитных волн. При этом в [25] рассматривался только случай    прямой связи между животными без учета боковой волны. В монографии [26] подробно рассмотрены характеристики антенн для связи в проводящей среде на низких частотах.    

Согласно [15], в СССР  в 60-е - 80–е годы  проводились эксперименты  по связи между погруженными горизонтальными диполями  в пресной и морской воде, показавшие возможность связи на расстояниях порядка 20 км на частоте 1 МГц.  Утверждается [15], что данные эксперименты не могут быть объяснены, исходя из классических  УМ,  и для их качественного объяснения  необходимо привлечь понятие продольной волны и модифицировать УМ.  Подробных количественных результатов эксперимента и сравнения с классической теорией ЭМВ в [15] не приведено. 

В данном разделе предпринят анализ экспериментов [15] на основе классических УМ. Показано, что качественное объяснение экспериментов [15]  согласуется со  следствиями из решения электродинамической задачи об излучении горизонтального диполя  под водой [22,27].  Количественное сравнение расчетных и экспериментальных данных  не могло быть проведено из-за недостатка  последних.

Приведем описание экспериментов [15]. Эксперименты были проведены на Черном море. Генератор мощностью до 400 Вт работал на частоте  1 МГц и размещался в герметичном  контейнере, расположенном  на пирсе.  К выводам генератора подключались кабели, концы которых погружались в воду и присоединялись к плоским электродам -  квадратным металлическим пластинам, установленным перпендикулярно поверхности моря. При включении между пластинами в морской воде возникает ток проводимости. Таким образом, излучатель представлял собой горизонтальный диполь, ось которого  параллельна поверхности моря.  Конструкция приемной антенны была аналогичной.  Детали передающей и приемной систем и проведения эксперимента изложены в [15].

                Принципиальная особенность рассматриваемой радиолинии заключается в том, что горизонтальные диполи должны быть направлены осями друг на друга. Как известно, подобная система при расположении диполей в воздухе не используется для дальней радиосвязи, т.к. в направлении оси диполя амплитуда поля убывает с удалением от диполя обратно пропорционально квадрату расстояния, а в дальней зоне этому направлению соответствует нуль диаграммы направленности.

В результате серии экспериментов была достигнута дальность передачи в поверхностном слое морской воды до 20 км на частоте 1 МГц [15].  Сигнал регистрировался приемником при опускании электродов на глубину не  более 2,5-3-х метров, на больших глубинах сигнал не принимался.  Другие подробности эксперимента см. в [15].

Результаты проведенного эксперимента, прежде всего сам факт установления надежной связи на расстоянии 20 км, а также накопленный опыт эффективной реализации передающей и приемной антенн представляют безусловный интерес и полезны для постановки аналогичных экспериментов в будущем.

Однако, по мнению автора [15], проведенные эксперименты подтверждают  существование ПЭМВ. Возражения вызывает именно попытка автора объяснить результаты эксперимента существованием ПЭМВ  без учета фундаментальных достижений классической электродинамики, известных к моменту проведения экспериментов.

Теоретическая задача об излучении горизонтального диполя, расположенного в полупроводящей среде параллельно плоской поверхности, отделяющей ее от внешней среды (вакуума), рассматривалась в большом числе работ в связи с анализом работы подземных  антенн и подводной радиосвязи.  Мы ограничимся  ссылками на  итоговые монографии [22,27].

Наглядная трактовка работы радиолинии между двумя горизонтальными вибраторами, ориентированными осями друг на друга,  приведена в параграфе  30 монографии [22] и показана на рис. 2.  Качественное объяснение  работы радиолинии состоит в следующем.  Пусть вибраторы расположены в полупроводящей среде на одинаковой глубине от границы раздела сред. Сигнал от передающего вибратора к приемному попадает двумя путями. Первый путь - по прямому направлению вдоль осей  от одного вибратора к другому без учета границы раздела сред.  По порядку величины   плотность потока мощности от передающего вибратора в этом направлении  равна

    ,                                                 (1)

где  α – постоянная затухания, x – расстояние между вибраторами.  В отсутствие потерь в среде (α=0) плотность потока мощности убывает обратно

пропорционально четвертой степени расстояния,  а при учете значительных потерь можно ограничиться учетом только  экспоненциального  затухания.

 

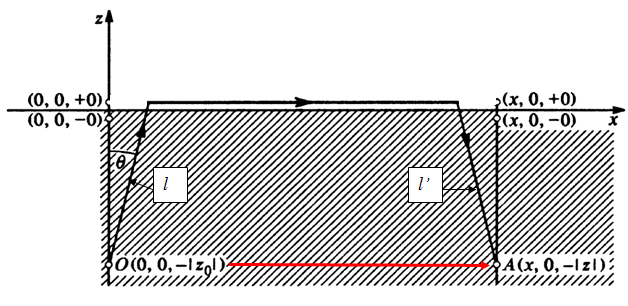
Рис. 2.  Распространение электромагнитного поля от передающего горизонтального диполя,
расположенного  под водной поверхностью в точке О (0,0,z₀ ),  до приемного горизонтального
диполя в точке О (0,0, z). Красная линия – прямой путь распространения поля между вибраторами.
Черная ломаная линия -  путь распространения поля по боковой волне. 

   

Второй путь соответствует возбуждению боковой волны [22]. Согласно лучевой трактовке поле вибратора идет от центра вибратора под углом θ к нормали относительно его оси  по пути l . Далее при  падении на границу раздела сред под критическим углом, равным , распространяется вдоль границы раздела сред по пути x’ и по пути l’=l попадает в приемную антенну. Предположим, что  │ε-i60λσ│>>1. Тогда можно положить, что  x’ ≈ x, l≈d,  где d  - глубина погружения диполя. В результате плотность потока мощности по суммарному пути  s=2l+x’  изменяется по закону [22]

    ,                                                     (2)

Из сопоставления ослабления плотности потока мощности на прямом пути (1) и    на боковом пути (2) следует, что в средах с  большими потерями     плотность потока мощности с ростом расстояния x убывает экспоненциально на прямом пути и степенным образом  -  на боковом пути. При этом вклад ослабления плотности потока мощности на боковом пути, обусловленный потерями в среде, мал при условии, что глубина погружения диполя мала по сравнению с глубиной проникновения поля в среду δ ≈1/α.

         Расчет ослабления поля по боковому пути проводится по приближенной  формуле (30.11)  монографии    [22].

         Несколько  иной подход изложен в [26]. Он базируется на строгом представлении  поля горизонтального диполя в полуограниченной поглощающей среде, полученном в интегральной форме. Представление поля было рассчитано  в [27] с применением специальных приемов  вычисления   быстроосциллирующих интегралов  и в окрестности точки ветвления.   В [27] было проведено также сравнение численных результатов с аппроксимирующими функциями, предложенными Баньосом.

Сопоставление методов [22] и [27] позволяет сделать предварительный вывод, что  различие  подходов должно сказаться только в ближней и промежуточной зонах диполя. В этой зоне расчетные формулы [27]  учитывают ослабление всех компонент электрического поля диполя порядка 1/d, 1/d², 1/d³ , где d -  расстояние от диполя, а в формулах  [22]  сохранено только слагаемое порядка 1/d, соответствующее дальней зоне (в приближенной формуле (2) предэкспоненциальный множитель этого порядка опущен). 

Для выяснения границ применимости  приближенных формул [22]  нами было проведено сравнение расчетов  по этим формулам с результатами [27].  При этом нормировка результатов [22]  проводилась по расчетам [27] на максимальной дальности, где можно было ожидать  согласия строгих [27]  и приближенных [22] формул. На рис. 3А приведено сравнение результатов [22]  и   [27]  для морской воды. Справа от точки пересечения кривых на уровне примерно  минус 100 дБ расчеты по строгой формуле [27],  формуле Баньоса для промежуточного поля и формуле   [22] графически совпадают.  Таким образом, приближение [22]  дает согласие с расчетами [27], начиная с расстояний  ≈ 8 м и более.

         Из результатов, представленных на рис.  3B ,  следует, что для пресной воды погрешность приближенной формулы [22] выше, чем для морской воды, тем не менее приближение [22] может быть использовано для грубых оценок ослабления сигнала с расстояний свыше 10 м. 

Исходя из приведенного сравнения, будем использовать приближение [21] для анализа энергетического потенциала радиолинии между двумя  горизонтальными диполями, погруженными в  соленую воду.  Потери в ближней  и промежуточной зонах диполя не учитываем, плотность потока мощности нормируем по ее значению на расстоянии 1 м от центра диполя. 

 

A)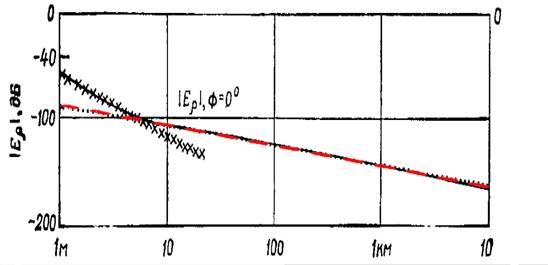

B)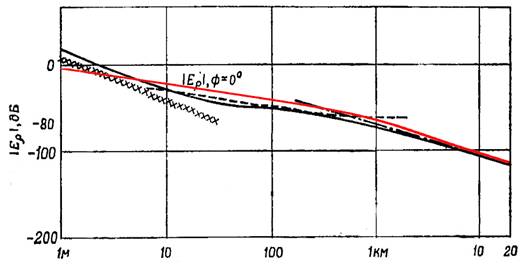

  

Рис. 3. Сравнение расчетов для радиальной компоненты электрического поля диполя по формулам [19] и  [27]

А) Морская вода, ε=80, σ=4 См/м, f=10 МГц, d=0,15 м, 

B)  Пресная вода ε=80, σ=0,004 См/м, f=10 МГц, d=0,15 м, 

Черные линии – расчеты [27] (A: рис. 11.7.1.в, B: рис. 11.7.2.[27] ) 

 

         На рис. 4 и 5  приведены зависимости уровня сигнала  между двумя соосными горизонтальными диполями, погруженными  в морскую воду с параметрами   ,  что соответствует солености S=35 ‰ (открытый океан). На рис. 4 даны результаты ослабления сигнала на различных частотах при расположении диполей  на глубине значительно меньше глубины проникновения (0,25 м на частоте 1 МГц).  Расчеты затухания поля по боковой волне проведены по формуле  (30.11) из [22],  расчеты затухания поля по прямой волне – по формуле (1). На рис.5  даны результаты расчета ослабления сигнала  на частоте 1 МГц по дальности при различных глубинах погружения  диполей.

 Из рис.4 и 5 следует, что на частоте 1 МГц затухание радиоволн в океане по боковой волне составляет от 80 дБ до  220 дБ на расстоянии 10 км  при погружении  диполей на глубину от 0 до  2 м.   Затухание по прямой составляет свыше 220 дБ на расстоянии более  8 между диполями. 

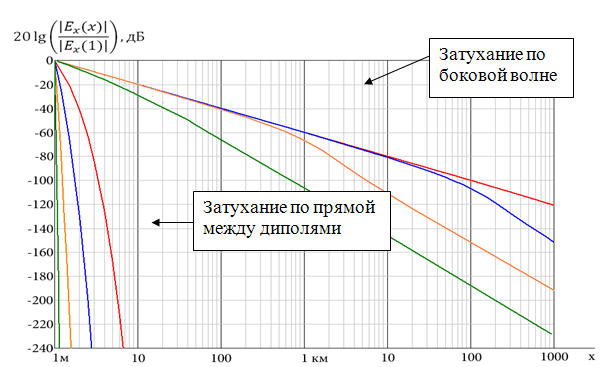
Рис. 4.  Сравнение зависимостей уровня сигнала от расстояния между горизонтальными диполями
в морской воде при передаче энергии боковой волной и по прямой на разных частотах.
Параметры воды: , , глубина погружения диполей –.

▬▬▬▬ 1 МГц; ▬▬▬▬ 10 МГц; ▬▬▬▬ 100 МГц; ▬▬▬▬ 1 ГГц.

 

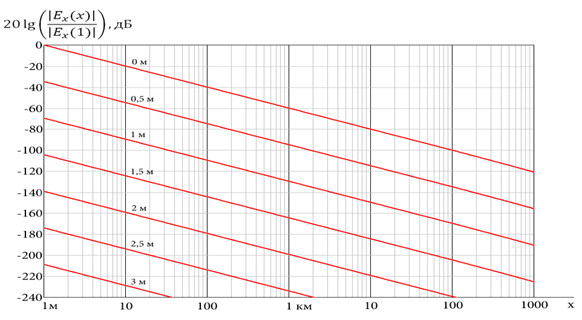
Рис. 5. Зависимость уровня сигнала от расстояния между горизонтальными диполями
в морской воде при передаче энергии боковой волной  и разных глубинах погружения диполей
 глубина указана на графиках. Частота 1 МГц. Параметры морской воды те же, что на рис.4

 

Аналогичные расчеты для Черного моря на частоте 1 МГц дали затухание радиоволн  по боковой волне на расстоянии 10 км от 80 дБ до  190 дБ при погружении  диполей на глубину от 0 до  2 м.  В то же время затухание по прямой составляет свыше 200 дБ на расстоянии более 7 м между диполями. 

При проведении расчетов оценочные значения проводимости морской воды были взяты из таблицы 6.11.1 [26] при температуре воды 15 ^оC для океана (соленость S≈35‰, проводимость 4,3 1/Ом*м) и для моря (соленость S≈20‰, проводимость 2,6 1/Ом*м).  В Черном море  на глубине до 50-100 м соленость воды составляет 18-21⁰/00, что меньше, чем в океане, соответственно меньше  электропроводность воды и затухание сигнала в дБ.  Более детальный количественный  анализ энергетического потенциала  подводной радиолинии нами не проводился  из-за неполноты экспериментальных данных [15]

Из  проведенных расчетов (см. рис. 4,5) следует, что ключевой результат экспериментов [15] - резкое ослабление сигнала при  погружении диполей на глубину свыше 2-3 м от поверхности морской воды объясняется  классической электромагнитной теорией передачи сигнала по боковой волне. 

Таким образом, объяснение экспериментов [15] с привлечением понятия продольной волны неубедительно, так как носит качественный характер и не основано на строгом электродинамическом анализе излучения диполя под водной поверхностью.  Прежде чем привлекать новые понятия, необходимо было показать неприменимость классической теории для объяснения экспериментов.

 

4. Заключительные замечания

         В данной статье приведено обсуждение  экспериментов  [11]  и [15], трактуемых авторами этих работ, как возбуждение ПЭМВ над или под земной поверхностью. Показано, что  экспериментальные результаты  этих работ   получают непротиворечивую трактовку с позиций классической электродинамики, не требуя привлечения эвристических  теорий, предполагающих существование ПЭМВ.    

Означает ли это, что не имеют смысла поиски и экспериментальное изучение   эффектов, которые при  предварительном рассмотрении  не согласуются с классической электродинамикой?  Ничего подобного!  Тщательно поставленный эксперимент стимулирует более глубокое изучение законов природы. Однако  для того, чтобы экспериментальные исследования способствовали движению вперед, необходимо, на наш взгляд,  выполнение как минимум следующих  достаточно очевидных условий.

1.     Постановка и результаты экспериментов  должны быть изложены с такой степенью подробности, чтобы они могли быть повторены независимыми научными группами и можно было провести сравнение с классической электродинамической теорией.

2.      В случае расхождения результатов эксперимента с классической теорией должны быть даны рекомендации по постановке новых экспериментов и /или по сопоставлению  с неклассическими теориями.   

С этих позиций целесообразно подходить и к анализу других экспериментальных   работ, претендующих на объяснение результатов с привлечением понятия ПЭМВ.  Наши выводы согласуются с оценкой состояния экспериментальных исследований,   данной в [17].

 

Литература

1.                Гинзбург В.Л. Распространение электромагнитных волн в плазме. -М.: Наука. 1969.   -683  с.

2.                 Агранович В.М., Гинзбург В.Л. Кристаллооптика с учетом пространственной дисперсии и теория экситонов. –М.: Наука. 1965, -374 с.

3.                 Бардзокас Д.И., Кудрявцев Б.А., Сеник Н.А.  Распространение волн в электромагнитоупругих средах. –М.: УРСС, 2003. -336 с.

4.                 Хворостенко Н.П. Продольные электромагнитные волны. // Изв. ВУЗов. Физика. – 1002.-№3. С. 24-29

5.                 Нефедов Е.И., Протопопов А.А. Обобщенная система уравнений электродинамики. // Электродинамика и техника СВЧ, КВЧ и оптических частот. 2000, т.8, вып. 3-4 (28), с.95-106.

6.                 Томилин А.К. Обобщенная электродинамика. – Усть-Каменогорск, ВКГТУ, 2009, - 168 с. 

7.                Протасевич Е.Т.. Некоторые особенности взаимодействия электромагнитных волн ТЕ- и ТЕМ-типов с металлами .  // Радиотехника и электроника, 1998, т. 43, №1, с.5-7.

8.       Колесников В.Н. и др. Способы передачи и приема электромагнитных волн через среду и устройства для их осуществления. Патент РФ на изобретение № 2143178 по заявке №98109181. Приоритет от 18.05.98, выдан 20.12.99.

9.      Tzontchev R.I., Chubukalo A.E., Rivera-Ju’arez J.M. Coulomb Interaction Does Not Spread Instantaneously // LANL arXiv: Physics/ 0010036 14 Oct 2000

10    Протасевич Е.Т. О возможности прохождения электромагнитных волн через металл // Труды 8-й международной конференции «Радиолокация, навигация, связь». (RLNC-2002). Воронеж, 2002, т.2, с. 1443-1448.

11.    Monstein C., Wesley J.P. Observation of scalar longitudinal electrodynamic waves. // Europhys. Lett. 59(4), pp. 514-520 (2002).

12.     Ермолаев Ю.М. Лампа накаливания и свеча как излучатели продольной ЭМВ //Электродинамика и техника СВЧ, КВЧ и оптических частот, 2004, т.12, вып. 3-4 (40), с.33-44.

13.      Konstantin Meyl, Scalar wave technology. 2001, ISBN 3980254267

14.      B. Sacco, A.K. Tomilin The Study of Electromagnetic Processes in the          Experiments of Tesla. //viXra.org > Classical Physics > viXra:1210.0158

15.    Ацюковский В. А. Эфиродинамические основы электромагнетизма. -М.: Энергоатомиздат, 2011,  194 c.

16.     Пермяков В.А. О продольных электромагнитных волнах. Критический

        анализ некоторых публикаций. // Электродинамика и техника СВЧ, КВЧ и  оптических частот, 2007, т. 15, вып. 1(43), с.30-39.

17.    Агеев И.М., Шишкин Г.Г. Продольные волны. –М.: МАИ, 2014, - 272 с.  

18.   Болотовский Б.М., Угаров В.А. Об одном «парадоксе» электродинамики. //УФН, 1976, т. 119, вып.2, с. 371-374

19.   Пермяков В.А. Анализ существования продольных электрических  волн в изотропной однородной среде. //Известия ВУЗов, Физика, 2012, т.55, № 8/3, с. 44-47.

20.  Bray J. R., Britton М.С. Comment on “Observation of scalar longitudinal electrodynamic waves” by C. Monstein and J.P. Wesley. // Europhys. Lett. 66 (1) pp.153–154 (2004)

21.  Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М-Л.: Энергия, 1967,- 376 с.   

22   Фейнберг Е.Л. Распространение радиоволн вдоль земной поверхности. 2-е изд. – М.: Наука. Физматлит, 1999. – 496 с.

23.   Rebilas K. On the origin of “longitudinal electrodynamic waves” //  Europhys. Lett., 83 (2008) 60007.

24.   Jack Althhouse. Build hydronic-radiation transmitter. // Radio electronics. 1967. Vol. 38, No.5. p. 37-38. 

25.  Остроумов Г.А. На каком расстоянии могли бы морские животные сообщаться при помощи электромагнитных волн // Дифракция и распространение радиоволн, 1968, вып.8, ЛГУ, с.3-24

26. Ольшанский В.М.  Бионическое моделирование электросистем слабоэлектрических рыб. –М.: Наука, 1990, - 208 с.  

27.    Кинг Р., Смит  Г. Антенны в материальных средах. Т.2, -М.:МИР, 1984, - 824 с.