ИСЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТЕМ РУПОРОВ
В. А. Калошин 1,2, К. З. Нгуен 2, Х. Ш. Нгуен 2
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 Московский физико-технический институт (государственный университет)
Статья получена 25 сентября 2015 г.
Аннотация. С использованием методов конечных элементов проведено численное моделирование характеристик согласования и излучения ТЕМ рупоров в сверхширокой полосе частот. Исследованы характеристики регулярного и двух типов нерегулярных ТЕМ рупоров с постоянным волновым сопротивлением - с монотонно возрастающими и монотонно убывающими величинами локальных углов раствора.
Ключевые слова: сверхширокополосные антенны, ТЕМ рупор, нерегулярный ТЕМ рупор.
Abstract: The numerical simulations of matching and radiation characteristics of TEM horns in UWB of frequencies were conducted with using the finite element method.The characteristics of regular horns and two types of irregular TEM horns with uniform impedance – with a monotonically increasing and monotonically decreasing value of the local angle of the solution are researched.
Key words: UWB antennas, TEM horns, irregular TEM horns, matching, radiation.
Введение
Регулярные и нерегулярные симметричные TEM рупоры являются излучателями, широко используемыми в качестве сверхширокополосных (СШП) антенн и их исследованию посвящено большое количество работ [1-19]. Геометрия регулярного (классического) ТЕМ рупора характеризуется тремя параметрами - длиной рупора L и углами раскрыва α и β (рис. 1), которые определяют характеристики его согласования и излучения. В случае нерегулярных ТЕМ рупоров (рис.2, 3), локальные углы α и β являются функциями, зависящими от продольной координаты. ТЕМ рупоры, в том числе нерегулярные, исследовались, главным образом, с точки зрения согласования [1–11]. Кроме того, следует отметить, что среди нерегулярных ТЕМ рупоров исследовались, главным образом, рупоры с переменным волновым сопротивлением. Характеристики излучения ТЕМ рупоров исследованы значительно меньше [2, 12–19]. При этом показано, что эти характеристики и, в частности, коэффициент усиления, немонотонно зависят от частоты. В работе [20] была исследована рупорно–линзовая антенна на основе регулярного металлодиэлектрического ТЕМ рупора. Эта антенна обладает монотонно возрастающим с увеличением частоты коэффициентом усиления (КУ) и высоким коэффициентом использования поверхности (КИП). Однако наличие диэлектрического заполнения и выполнение выходной поверхности в форме линзы приводит к усложнению конструкции рупора и увеличению его веса.
В данной работе проводится исследование характеристик ТЕМ рупоров без диэлектрического заполнения. Исследованы как широко известные типы ТЕМ рупоров, в которых углы α и β являются постоянными или монотонно возрастающими функциями продольной координаты, так и рупоры с монотонно уменьшающимися по направлению к апертуре углами α и β.
Для исследования характеристик согласования и излучения геометрия всех ТЕМ рупоров была выбрана таким образом, чтобы импеданс Z = 150 Ом оставался постоянным в любом сечении рупора. Это достигается за счет выбора примерно одинаковых значений локальных значений углов α и β в каждом сечении, в результате чего обеспечивается квадратная выходная апертура. Длины рупоров L подбирались таким образом, чтобы размеры апертуры были примерно равны 100 х 100 (мм). Углы регулярного ТЕМ рупора (рис.1) при этом составили: α = 700, β = 620, длина L = 100мм.
Первый тип нерегулярного ТЕМ рупора (рис.2) – широко известный ТЕМ рупор с монотонно увеличивающимися величинами углов α и β. В работе рассматриваются два варианта изменения ширины рупора: с экспоненциальной и квадратичной формой образующей.
- Для ТЕМ рупора с экспоненциальной образующей, где зависимость ширины и расстояния между пластинами рупора от продольной координаты:
где a0 = h0 = 1мм –
ширина и расстояние между пластинами рупора в узле возбуждения, ![]() ,
и
,
и ![]() ,
, ![]() и
и ![]() – размер апертуры рупора (рис.2), L - длина
рупора по продольной координате.
– размер апертуры рупора (рис.2), L - длина
рупора по продольной координате.
- Для ТЕМ рупора с квадратичной образующей:
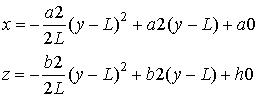 (2)
(2)
где ![]() и
и ![]() , начальные
углы в узле возбуждения α1 = 770, β1 = 700, L - длина рупора
по продольной координате.
, начальные
углы в узле возбуждения α1 = 770, β1 = 700, L - длина рупора
по продольной координате.
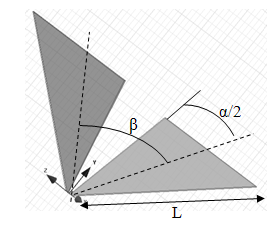
Рис.1. Регулярный ТЕМ рупор
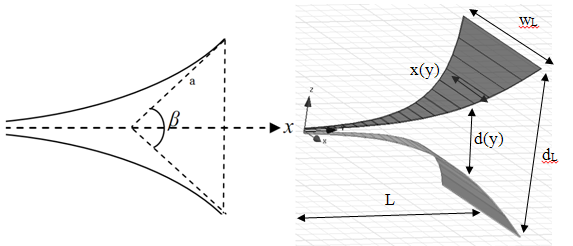
Рис. 2. Нерегулярные ТЕМ рупоры 1-го типа
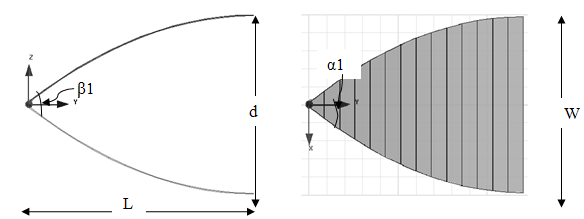
Рис. 3,4. Нерегулярные ТЕМ рупоры 2-го типа
Для нерегулярных ТЕМ рупоров второго типа - с монотонно уменьшающимися величинами углами α и β (рис.3,4) форма образующих описывается выражениями:
- Для ТЕМ рупора с экспоненциальной образующей:
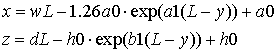 (3)
(3)
- Для ТЕМ рупора с квадратичной образующей:
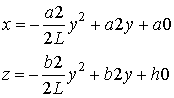 (4)
(4)
1. Характеристики согласования ТЕМ рупоров
Как показано в работе [2] для оценки нижней границы частот согласования для регулярного и нерегулярного ТЕМ рупоров 1-го типа можно использовать асимптотическую теорию отражения от конца двумерного рупора, развитую в работе [21]. Выражение для первого члена коэффициента отражения может быть представлено в следующем виде:
где k – волновое число в пространстве; g(0,0,2) = -1 – дифракционный коэффициент, описывающий решение задачи дифракции плоской волны на полуплоскости; β – угол образующей касательными линиями от конца рупора (рис. 2);
Для оценки нижней границы частот согласования нерегулярных ТЕМ рупоров 2-го типа будем использовать формулу Вайнштейна [22] для коэффициента отражения от открытого конца двумерного волновода:
где d = d(L) – размер апертуры ТЕМ рупора в Е – плоскости (рис.3)
На рис.5 представлены зависимости коэффициента отражения от частоты регулярного ТЕМ рупора разной длины L = 100 мм (синие штриховые линии), L = 127мм (красные штриховые линии), вычисленные с использованием метода конечных элементов, а также с использованием асимптотической формулы (5) (сплошные линии). В качестве питающей линии здесь и далее использована двухпроводная симметричная микрополосковая линия с импедансом 150 Ом.
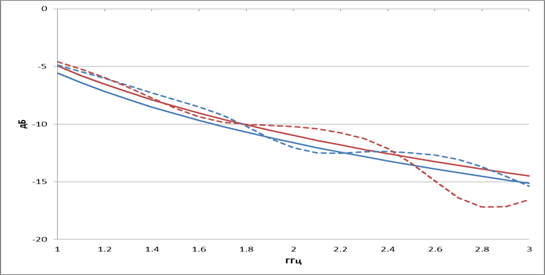
Рис.5. Зависимость коэффициента отражения регулярного ТЕМ рупора от частоты
Как видно на рисунке асимптотическая формула неплохо предсказывает нижнюю частоту согласования рупора (по уровню -10 дБ).
Для нерегулярных ТЕМ рупоров 1-го типа зависимости коэффициента отражения от частоты представлены на рис. 6 и рис. 7, соответственно, для рупора с экспоненциальной и квадратичной образующей. Синими и красными линиями показаны, соответственно, результаты для рупора с длиной L = 110 мм и 165мм. Штриховыми и сплошными линиями приведены результаты, полученные с использованием метода конечных элементов и асимптотической формулы (5), соответственно.
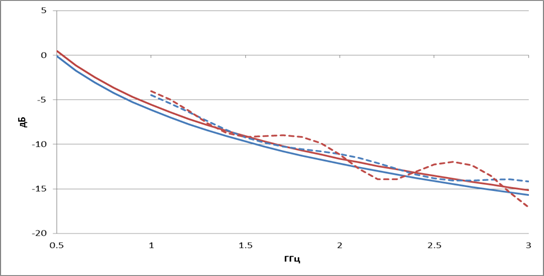
Рис.6. Зависимость коэффициента отражения нерегулярного ТЕМ рупора 1-го типа с экспоненциальной образующей от частоты
Как и в предыдущем случае, асимптотическая формула неплохо предсказывает нижнюю частоту согласования нерегулярного рупора1-го типа с экспоненциальной образующей. Можно также отметить слабое влияние длины рупора на характеристики согласования.
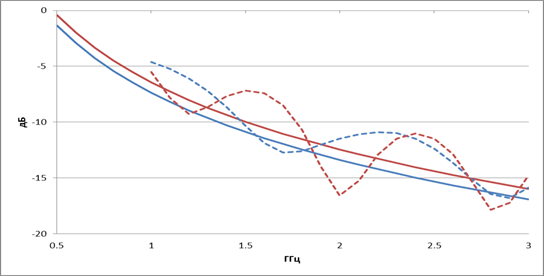
Рис.7. Зависимость коэффициента отражения нерегулярного ТЕМ рупора 1-го типа с квадратичной образующей от частоты
Для нерегулярного ТЕМ рупора 1-го типа с квадратичной образующей характеристики согласования становятся более изрезанными, а формула (5) хуже предсказывает нижнюю частоту согласования.
На рис.8 представлены зависимости коэффициента отражения от частоты нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей разной длины L = 73.3 мм (синие штриховые линии), L = 110 мм (красные штриховые линии), вычисленные с использованием метода конечных элементов, а также с использованием формулы (6) (сплошные линии). Как видно на рисунке, в этом случае также наблюдаются сильные колебания коэффициента отражения от частоты. Формула (6) хорошо предсказывает нижнюю границу согласования только для короткого рупора.
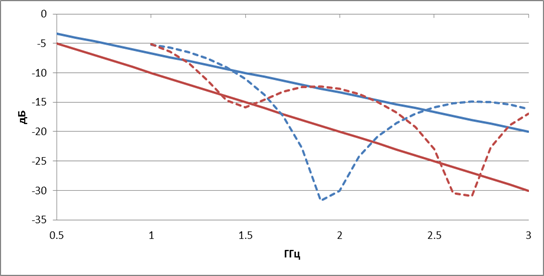
Рис.8. Зависимость коэффициента отражения нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей от частоты
На рис.9 представлены зависимости коэффициента отражения от частоты нерегулярного ТЕМ рупора 2-го типа с квадратичной образующей разной длины L = 87 мм (синие штриховые линии), L = 130 мм (красные штриховые линии), вычисленные с использованием метода конечных элементов, а также с использованием формулы (6) (сплошные линии). Как и в предыдущем случае, формула (6) хорошо предсказывает нижнюю границу согласования только для короткого рупора.
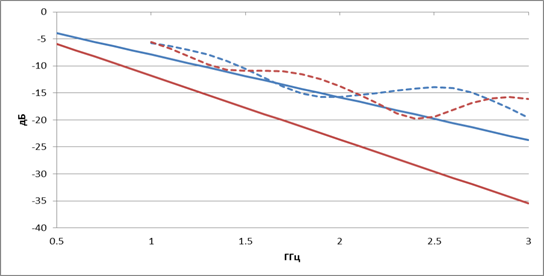
Рис.9. Зависимость коэффициента отражения нерегулярного ТЕМ рупора 2-го типа с квадратичной образующей от частоты
На рис.10. представлены зависимости коэффициента отражения ТЕМ рупоров от частоты: для регулярного ТЕМ рупора (синяя линия) – длина 100 мм, углы α = 700 и β = 620; для нерегулярных ТЕМ рупоров 1-го типа с экспоненциальной образующей (красная сплошная) и с квадратичной образующей (красная штриховая) – длины 110 мм, углы α = 770 и β = 700, для нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей (зеленная сплошная) – длина 110 мм, углы α = 770 и β = 700; с квадратичной образующей (зеленная штриховая) – длина 130 мм, углы α = 770 и β = 700.
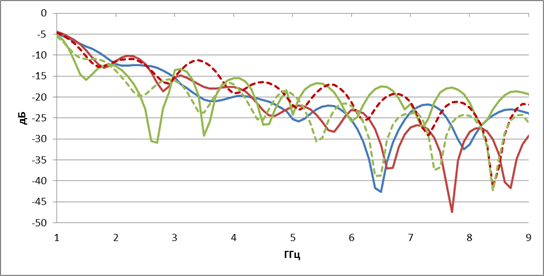
Рис.10. Зависимость коэффициента отражения ТЕМ рупоров от частот
Качество согласования оценим с помощью введенного в работе [23] коэффициента использования размера (КИР), равного отношению диаметра сферы Чу [23] к диаметру описанной вокруг антенны сферы.
Величины КИРа исследованных ТЕМ рупоров приведены в таблице 1.
Таблица 1
|
Тип рупоров |
Длина рупора (мм) |
КИР |
|
Регулярный ТЕМ рупор |
100 |
0.20 |
|
Нерегулярный ТЕМ рупора 1-го типа с экспоненциальной образующей |
110 |
0.21 |
|
Нерегулярный ТЕМ рупора 1-го типа с квадратичной образующей |
110 |
0.23 |
|
Нерегулярный ТЕМ рупора 2-го типа с экспоненциальной образующей |
110 |
0.27 |
|
Нерегулярный ТЕМ рупора 2-го типа с квадратичной образующей |
130 |
0.24 |
Можно отметить, что все величины КИРа находятся примерно на одном, достаточно низком уровне с учетом того, что максимальные значения КИР для нерегулярных ТЕМ рупоров к настоящему времени достигли величин 0.5 – 0.7 (см. [2, 3]). При этом максимальную величину КИРа имеет нерегулярный ТЕМ рупора 2-го типа с экспоненциальной образующей, что, вообще говоря, теорией не предсказывается.
2. Характеристики излучения ТЕМ рупоров
Для исследования характеристик усиления и излучения выбраны теже же параметры ТЕМ рупоров, как и в таблице 1.
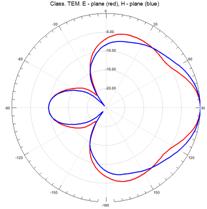
На рисунках 11–15 приведены результаты моделирования диаграмм направленности ТЕМ рупоров методом конечных элементов в Е – плоскости (красные линии) и в Н – плоскости (синие линии) на трех частотах: 3 ГГц (а), 5 ГГц (б) и 7 ГГц (в).
|
|
|
|
Рис.11. Диаграммы направленности регулярного ТЕМ рупора
|
|
|
|
Рис.12. Диаграммы направленности нерегулярного ТЕМ рупора 1-го типа с экспоненциальной образующей
|
|
|
|
Рис.13. Диаграммы направленности нерегулярного ТЕМ рупора 1-го типа с квадратичной образующей
|
|
|
|
Рис.14. Диаграммы направленности нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей
|
|
|
|
Рис.15. Диаграммы направленности нерегулярного ТЕМ рупора 2-го типа с квадратичной образующей
На рис.11 – 15, видно, что наиболее изрезанными являются диаграммы направленности ТЕМ рупоров в Е– плоскости. При этом максимальная изрезанность наблюдается у нерегулярных ТЕМ рупоров 2-го типа, а минимальная у нерегулярного ТЕМ рупора 1-го типа с экспоненциальной образующей.
На рис.16 синей линией показана рассчитанная методом конечных элементов зависимость коэффициента усиления от частоты регулярного ТЕМ рупора, красной сплошной линией - нерегулярного ТЕМ рупора 1-го типа с экспоненциальной образующей, красной штриховой линией - нерегулярного ТЕМ рупора 1-го типа с квадратичной образующей, зеленой сплошной линией - нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей, зеленой штриховой линией - нерегулярного ТЕМ рупора 2-го типа с квадратичной образующей.
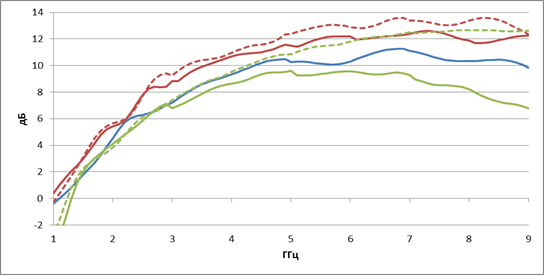
Рис.16. Зависимость коэффициенты усиления ТЕМ рупоров от частоты
Как и в случае классических рупоров, коэффициенты усиления ТЕМ рупоров на низких частотах с ростом частоты растут, достигают максимума и затем убывают. При этом максимальные коэффициенты усиления обеспечивают нерегулярные ТЕМ рупоры 1-го типа. На высоких частотах близкие результаты у рупора 2-го типа с квадратичной образующей, минимальное усиление – у нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей.
Заключение
На основании проведенных в работе исследований можно сделать следующие выводы:
1. Несмотря на постоянство локального импеданса исследованных ТЕМ рупоров (150 Ом), они не обладают улучшенным согласованием по отношению к ТЕМ рупорам с переменным импедансом и входным импедансом 50 ом. Более того, величина КИР исследованных рупоров в 2-3 раза меньше по сравнению с оптимизированными рупорами с переменным импедансом.
2. Приближенные аналитические формулы позволяют оценить нижнюю границу согласования рупоров различного типа по уровню -10 дБ. Наиболее точной получается такая оценка для коротких рупоров. Последнее можно объяснить меньшим влиянием на коэффициент отражения вытекающего характера рупорной моды.
3. Все исследованные рупоры обладают изрезанной формой диаграммы направленности на высоких частотах. При этом минимальной изрезанностью обладает диаграмма направленности нерегулярного ТЕМ рупор 1-го типа с экспоненциальной образующей.
4. Максимальное усиление и, соответственно, КИП имеет нерегулярный ТЕМ рупор 1-го типа с квадратичной образующей, близкие к нему результаты - нерегулярный ТЕМ рупор 1-го типа с экспоненциальной образующей и рупор 2-го типа с квадратичной образующей. Минимальное усиление – у нерегулярного ТЕМ рупора 2-го типа с экспоненциальной образующей.
Литература
1. Lee R.T., Smith G.S. A design study for the basic TEM horn antenna // IEEE Antennas and Propagation Society International Symposium, June 2003. Vol.1. pp. 225-228
2. Ефимова Н.А., Калошин В.А., О согласовании симметричных ТЕМ рупоров // Радиотехника и электроника, 2014. том 59. № 1, 60-66
3. Бирюков В.Л., Ефимова Н.А., Калиничев В.И., Калошин В.А., Пангонис Л.И. Исследование сверхширокополосной кольцевой антенной решетки // Журнал радиоэлектроники: электронный журнал., 2013, №1 URL: http://jre.cplire.ru/jre/jan13/20/text.pdf
4. Jinjin Sh., Guangyou F., Jingjing F., Yicai J., Hejun Y. TEM Horn antenna loaded with absorbing material for GPR applications // IEEE Antennas and Wireless Propagation Letters, 2014. Vol. 13. pp. 523-527
5. Chung K. H., S. H. Pyun, and J. H. Choi. Design of an ultrawide-band TEM horn antenna with amicrostrip-type balun // IEEE Transactions on Antennas and Propagation, , October 2005. Vol.53. №. 10, pp. 3410 - 3413
6. Majid Manteghi., Yahya Rahmat-Samii. A novel UWB feeding mechanism for the TEM horn antenna, reflector IRA, and theVivaldi antenna. IEEE Antennas and propagation Magazine, October 2004. Vol. 46. №. 5, pp. 81 – 87
7. Bassam S., Rashed-Mohassel J. A Chebyshev Tapered TEM Horn Antenna // Progress In Electromagnetics Research Symposium Online, 2006. Vol. 2. № 6
8. Kao Ch.-P., Li J., Liu R. Design and Analysis of UWB TEM Horn Antenna for Ground Penetrating Radar Applications // IEEE International Geoscience and Remote Sensing Symposium, July 6-11 2008, Boston, USA, pp. 569-572
9. Ameri A.A.H., Kompa G., Bangert A. Study About TEM Horn size reduction for Ultra-Wideband Radar Application // Proceedings of the 6th German Microwave Conference March 14-16 2011, Darmstadt, Germany pp. 1–4
10. Jinjin Sh., Guochang L., Yicai J., Guangyou F., Hejun Y. UWB TEM horn antenna for the asphalt pavement investigation // Journal of Electronics (China), Feb. 2014. Vol. 31. № 1, pp. 1–5
11. Singh S.K., Sarkar B.K. Effect of aperture matching on the performance of TEM horn antenna // 1st International Conference on Emerging Technology Trends in Electronics, Communication and Networking, Gujarat, India, 19 Dec - 21 Dec 2012. pp. 1–5
12. A. R. Mallahzadeh., F. Karshenas. Modified TEM horn antenna for broadband applications // Progress In Electromagnetics Research, PIER 90, 2009. pp. 105–119
13. Daniel Oloumi, Pedram Mousavi, Mats I. Pettersson,. Duncan G. Elliott. A modified TEM horn antenna customized for oil well monitoring applications // IEEE Transactions on Antennas and Propagation, December 2013. Vol.61. № 12, pp. 5902 – 5909
14. Malherbe J.A.G. Hybrid elliptic TEM horn with symmetric main beam // Antenna Technology and Applied Electromagnetics (ANTEM), 2012 15th International Symposium on 25-28 June 2012. Toulouse, pp. 1-4
15. Koshelev V. I., Buyanov Y. I., Koval'chuk B.M., и др. High-power ultra wideband electromagnetic pulse radiation // Proc. SPIE, 1997. Vol. 3158, pp. 209-219
16. Amjadi H., Hamedani F.T. A Novel 2-18 GHz TEM Double-Ridged Horn Antenna for Wideband Applications // 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, 26 Jul - 30 July 2011 Harbin, Heilongjiang, China. pp 341-344
17. Бобрешов А.М., Мещеряков И.И., Усков Г.К. Оптимизация геометрических параметров ТЕМ-рупора для излучения сверхкоротких импульсов в составе антенной решетки с управляемым положением главного лепестка // Радиотехника и электроника. 2013. Т. 58, № 3, С. 233-237
18. Campbell M.A., Okoniewski M., Fear E.C. TEM horn antenna for near-field microwave imaging // Microwave and Optical Technology Letters, 2010. pp. 1164–1170.
21. Kaloshin V.A., Scattering matrix for a junction of two horns // RJMP, 2009. Vol. 16. №. 2, pp. 246–250.
22. Вайнштейн Л.А. Теория дифракции и метод факторизации. М.: «Советское радио», 1966
23. Chu L.J. Physical limitations of Omni-directional antennas // Journal of Applied Physics, 19, December 1948. pp. 1163-1175
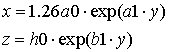
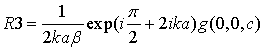
 а)
а)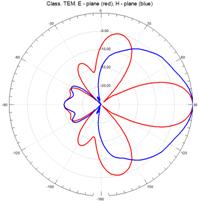 б)
б)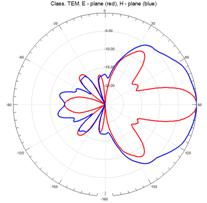 в)
в)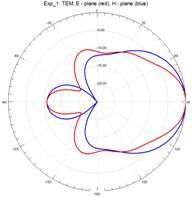 а)
а)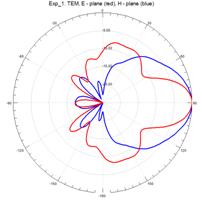 б)
б)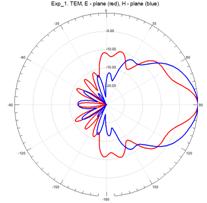 в)
в)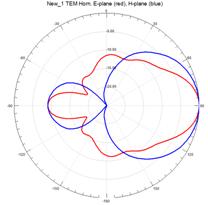 а)
а)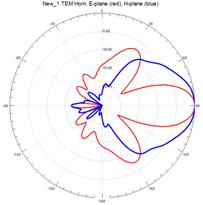 б)
б)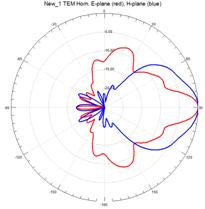 в)
в)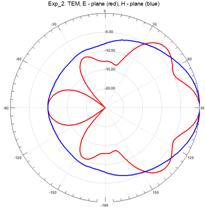 а)
а)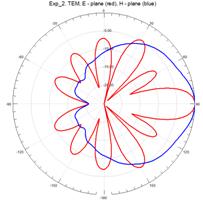 б)
б)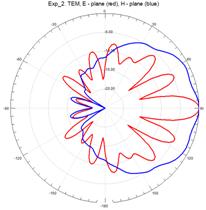 в)
в)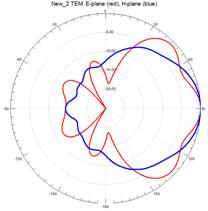 а)
а)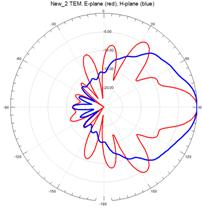 б)
б)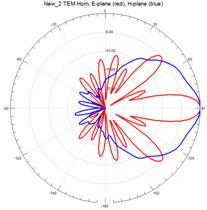 в)
в)