УДК 621.371.5; 550.388.2

Метод обнаружения сигнала ЛЧМ-ионозонда в частотной области с учетом уширения принимаемых мод ионосферного распространения

 

А. Е. Недопекин

Марийский государственный университет

 

Статья поступила в редакцию 28 сентября 2015 г., после доработки – 14 октября 2015 г.

 

Аннотация. В статье рассмотрен метод обнаружения сигнала ЛЧМ-ионозонда в частотной области. Метод учитывает принадлежность к выделяемой моде ионосферного распространения отсчетов, не являющихся аномальными для рассматриваемой выборки. В основе метода лежит двухэтапное цензурирование выборки с использованием критерия выделения аномальных отсчетов и порогового критерия, учитывающего эмпирическую оценку уширения моды.

Ключевые слова: ионосфера, выделение сигнала, коротковолновой канал, частотно-временная дисперсия, случайно-неоднородная среда.

Abstract: The article describes a method for isolating the signal chirp ionosonde in the frequency domain. The method takes into account that the mode of ionospheric propagation contains readings that are not abnormal for the given sample. The method is based on a two-stage sampling censoring based on the criterion of abnormal discharge readings and threshold criteria, taking into account the empirical evaluation of the broadening of  the mode.

Key words: ionosphere, extraction of signal, short-wave channel, time-frequency dispersion, randomly inhomogeneous medium.

Введение

В радиофизических исследованиях ионосферы и при диагностике коротковолновых каналов радиосвязи активно применяются ионозонды, использующие сигнал с линейной частотной модуляцией (ЛЧМ-ионозонды). Преимущество ЛЧМ-ионозонда заключается в использовании сигнала с большой базой, излучаемого непрерывно в полосе частот, совпадающей с полосой декаметрового (ДКМ) канала [1]. Это позволяет достигнуть хорошей помехоустойчивости при малом энергопотреблении и широком частотном диапазоне измерений. Но в широкую полосу полезного ЛЧМ-сигнала, имеющего скорость перестройки частоты 100-500 кГц/с, попадают сигналы радиотехнических устройств (РПУ), работающих в каналах, через которые проходит зондирующий сигнал. Сигналы эти, обладающие различной частотно-временной структурой, способны менять законы распределения смеси сигнал-шум. Так же при приеме зондирующего сигнала значительно выражена частотно-временная дисперсия, обусловленная нестационарным характером канала [2] и случайно-неоднородной структурой среды распространения сигнала [3]. Последние из указанных факторов вызывают замирания огибающих сигнала, искажения фазочастотных характеристик, вызывают рассогласование при приеме широкополосных сигналов. Это препятствует расширению использования ДКМ диапазона, затрудняет автоматическое обнаружение зондирующего ЛЧМ сигнала на спектрограмме при физических измерениях.

В работах [4, 5] рассмотрено обоснование методов обнаружения сигнала в частотной области на основе рассмотрения полезного сигнала как совокупности аномальных отсчетов в выборке, чья статистика обусловлена шумами и помехами от посторонних РПУ. В качестве критериев обнаружения был предложен критерий, использующий 95% квантиль цензурируемой выборки, и критерии, основанные на модифицированных статистиках цензурирования (статистики Кохрена и Граббса). Однако опытное использование разработанных критериев выявило их недостаток, который может быть ощутимым при радиофизических измерениях и квазиоптимальном приеме [6] широкополосного ЛЧМ сигнала. Выделяя наиболее мощные гармоники сигнала, критерии часто считают аномальными не все гармоники, принадлежащие уширению сигнала и дополнительной многолучевости, обусловленной неоднородностью канала земля-ионосфера. Повышение же чувствительности критериев приводит к росту количества ложных выделенных отсчетов.

Целью работы является разработка метода обнаружения сигнала ЛЧМ-ионозонда в частотной области с учетом необходимости выделения статистически неаномальных отсчетов моды.

2. Критерии обнаружения

Принятый сигнал ионосферного распространения умножается в приемнике на сигнал, когерентный излученному, после чего фильтр нижних частот отделяет сигнал разностной частоты. Он представляет собой смесь полезного сигнала, шумов ДКМ-диапазона и помех. Сигнал проходит оцифровку и обрабатывается при помощи дискретного преобразования Фурье элементами с произвольной длительностью (обычно 1 с) с получением для каждого элемента спектральной плотности мощности. В результате для всего сеанса зондирования строится спектрограмма (ионограмма). Обнаружение полезного многомодового сигнала производится по спектральной плотности мощности разностного сигнала. При этом с точки зрения радиофизических измерений важно выделить сигнал моды как можно полнее. Для обнаружения сигнала в спектральной области возможно использование статистических критериев, основанных на цензурировании выборки. При этом в роли аномальных отсчетов выступают отсчеты сигнала. Рассмотрим два таких критерия.

Первый критерий исходит из предположения, что доля аномальных отсчетов не превосходит 95% от выборки размера . Берется 95% квантиль  и определяется максимально возможный доверительный интервал как произведение среднеквадратического отклонения  и энтропийного коэффициента , вычисленных по первым  отсчетам вариационного ряда. Энтропийный коэффициент оценивается по гистограмме из соотношения [7]:

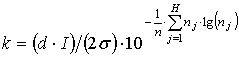,                                      (1)

 

где  — ширина столбца гистограммы,  — число столбцов гистограммы для первых 95% выборки,  — число элементов в j-м столбце гистограммы.

Каждый тестируемый отсчет  выборки проверяется условием вида . Если условие выполняется, то отсчет считается аномальным, что в случае частотного спектра соответствует выделенной гармонике сигнала.

Второй критерий использует для тестирования отсчета  статистику Кохрена

, , .                 (2)

 

Критические значения статистики  определяются по формуле

,                                                   (3)

полученной по результатам полуэмпирического моделирования выборок в [5], где  — эксцесс выборки, соответствующей первым 90% вариационного ряда. Превышение величиной  критического значения означает выделение  как аномального.

По результатам применения критерия для ионограммы создается такого же размера массив индикаторов, принимающих значение 1, если соответствующий отсчет в ионограмме выделен как сигнал, и нуль в противном случае. Случайные выбросы, которые так же выделяются вместе с сигналом, фильтруются в массиве индикаторов с использованием скользящего квадратного медианного фильтра с нечетной апертурой. Отсчеты, попадающие в окно размера , выстраиваются в вариационный ряд (по возрастанию), после чего центральному элементу окна присваивается значение медианного отсчета. После фильтрации все оставшиеся значения индикаторов, равные единице и окруженные в радиусе одного отсчета менее чем  единицами, подлежат обнулению. Пример ионограммы для сеанса Lyon (Франция) — Йошкар-Ола (100 кГц/с, 24.04.2010 г, 21:21 UTC) приведен на рис. 1а). На рис. 1б) — соответствующий ей массив индикаторов после применения критерия Кохрена, на рис. 1в) — массив индикаторов после фильтрации фильтром  и порогом , равным 1.

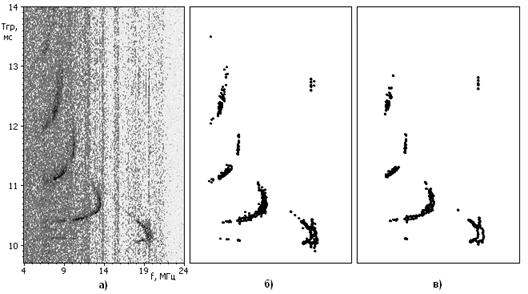
Рис. 1 а) Пример ионограммы до обнаружения сигнала, б) после обнаружения сигнала, в) после фильтрации

3. Неаномальные отсчеты моды

Как видно из сравнения рис. 1а) и рис. 1б), не всем отсчетам ионограммы, которые можно считать принадлежащими модам сигнала, соответствуют единичные индикаторы после применения критерия. На рис. 2 показаны примеры спектров мощности и обнаруженных в них аномальных отсчетов с использованием критерия со статистикой Кохрена и фильтром  () для сеансов на трассах Норильск — Йошкар-Ола (500 кГц/с) (рис. 2а) и Lyon — Йошкар-Ола (100 кГц/с) (рис. 2б).

Принятый сигнал на рис. 2 является двухмодовым, максимумы в спектре мощности соответствуют для случая а) одно- и двухскачковым отражениям от ионосферного слоя , для б) — двух- и трехскачковым отражениям от . На обоих рисунках вторая мода имеет гораздо большее уширение, чем первая, что связанно с траекторией сигнала, включающей большее число отражений от ионосферы и земной поверхности [3].

В [2,3,8] в приближении геометрической оптики и c использованием моделей ионосферных неоднородностей было показано, что наблюдаемое уширение сигналов не может быть объяснено одними лишь эффектами дискретного преобразования Фурье, применяемого для перевода сигнала в частотную область. Получаемые на опыте уширения имеют больший частотный диапазон в разностном спектре (особенно для многоскачковых мод), а так же могут иметь признаки дополнительной многолучевости в узком диапазоне частот, что видно для вторых мод на рис. 2 а) и б).

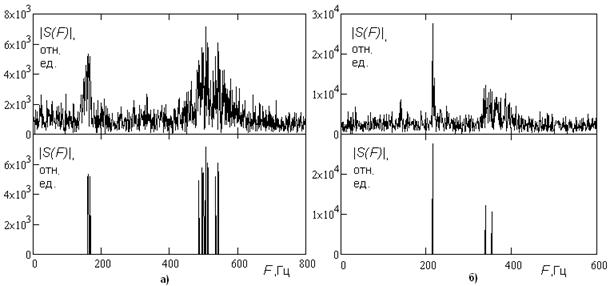
Рис. 2. Примеры спектров сигнала после процедуры обнаружения

Из рис. 2 видно, что далеко не все отчеты, принадлежащие модам, обнаружены использованным критерием. В то же время установлено, что пропущенные отсчеты, как правило, превышают средний уровень шумов на величину, достаточную для обнаружения отсчетов. Из [5] известно, что при работе критериев равновероятностная ошибка 5% достигается при отношении мощности сигнала к мощности шумового фона 8-9 дБ. Это значит, что отсчеты сигнала, не являющиеся аномальными, можно с малым риском ошибки выбирать из тех, которые не были выделены критерием, но превышают на 8-9 дБ уровень шума в некоторой окрестности уже выделенных отсчетов моды. Для этого предлагается саму процедуру обнаружения сигнала разбить на два основных этапа. Первый этап: выделение аномальных отсчетов. Второй этап: выбор отсчетов вблизи аномальных в окрестности величины , соответствующей оценке уширения моды. Выбор должен производиться из числа тех отсчетов, что превышают порог обнаружения сигнала. Определение отсчетов, превышающих порог и подозрительных на принадлежность сигналу, производится в выборке после замены аномальных отсчетов на средние значения, полученные в окне размера . На рис. 3 приведен пример спектра сигнала из рис. 2б), на который наложены две регрессионных кривые, описываемые полиномами пятой степени.

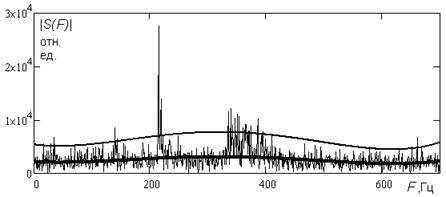
Рис. 3 Спектр сигнала с огибающей шумов и порогом обнаружения

Кривые получены следующим образом. Из выборки вначале были устранены аномальные отсчеты, выделенные критерием Кохрена, с заменой их на средние значения в окне , соответствующем времени задержки 1 мс. Подбор величины  должен обеспечить усреднение по числу отсчетов, большему, чем возможная ширина моды, в противном случае заменяющее значение может быть слишком велико. В данной работе  соответствует оценке среднего расстояния между модами в спектрограмме. Центр окна принимался равным месту положения заменяемого отсчета в выборке. Далее полученная выборка сглаживалась медианным фильтром с апертурой . Для полученных данных строилась регрессионная кривая , соответствующая сглаженной огибающей шума (на рисунке жирная) и кривая , соответствующая уровню в 8 дБ относительно первой кривой (на рисунке тонкая).

Все отсчеты, превышающие вторую кривую, являются кандидатами на выделение в качестве отсчетов сигнала, но среди них есть случайные выбросы. Поэтому считается, что отсчет-кандидат должен быть близок по своему положению в выборке к аномальным отсчетам, выделенным на первом этапе. Для этого необходимо иметь априорные представления о возможной ширине моды принимаемого сигнала в спектре. Для определения величины окрестности  необходимо исходить из некоторых верхних оценок частотно-временной дисперсии и уширения, вызванного неоднородной структурой среды распространения сигнала. При этом привлечение модельных расчетов в зависимости от неоднородности электронной концентрации [9], географии трассы и ландшафта земной поверхности представляется громоздким и требующим большого количества дополнительной информации. Это неудобно для автоматической обработки спектрограмм, поэтому величина  принимается равной числу подозрительных отсчетов, попадающих в окно . Априори считается, что все эти отсчеты должны принадлежать уширению моды. Естественно, что не все из них окажутся в -окрестности аномальных отсчетов. Такие удаленные отсчеты не будут считаться принадлежащими сигналу.

4. Алгоритм обнаружения

Основываясь на изложенных соображениях, можно сформулировать следующий алгоритм обнаружения полезного сигнала в частотной области, интерпретирующий спектральную плотность мощности элемента сигнала как массив данных размера .

1.         Выделение аномальных отсчетов в каждой спектральной выборке  одним из представленных критериев выделения. Фильтрация случайных выбросов для всего двумерного массива индикаторов .

2.         Оценка среднего расстояния  между модами сигнала по массиву, полученному усреднением всех столбцов бинарного массива индикаторов, соответствующих спектрам, в которых были выделены отсчеты сигнала.

3.         Замена всех выделенных аномальных отсчетов в каждом  на средние значения в окне , где i — номер заменяемого аномального отсчета в выборке. Получение новых выборок .

4.         Медианная фильтрация выборок  с окном, равным  и получение массивов .

5.         Построение для каждого массива  регрессионной кривой  в виде полинома 5-7-ой степени.

6.         Определение в массиве  для всех подвыборок размера  положения  максимальных аномальных отсчетов и количества  отсчетов массива , больших, чем значение  и принадлежащих . Эти отсчеты образуют подмножество отсчетов, подозрительных на принадлежность к сигналу.

7.         Все подозрительные отсчеты, в -окрестности которых присутствуют аномальные отсчеты, считаются принадлежащими сигналу. Этим отсчетам соответствует свой массив индикаторов .

8.         Поэлементная дизъюнкция массивов  и . Фильтрация полученного массива, как в пункте 1. Поэлементное умножение спектрограммы на результирующий массив.

На рис. 4 представлен пример использования алгоритма в сравнении с простым выделением аномальных отсчетов, которому соответствует первый пункт приведенного алгоритма. В качестве спектрограммы взяты спектрограммы для сеансов из примера на рис. 2.

 

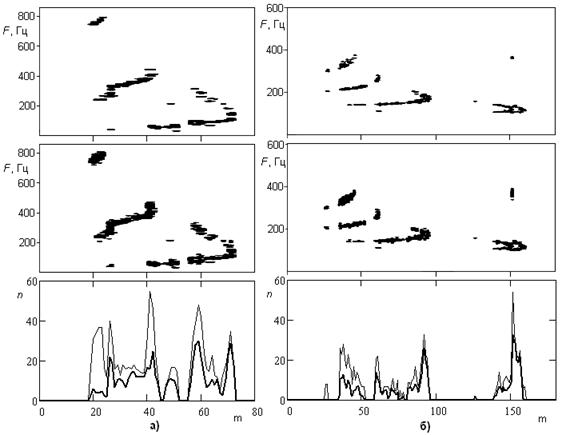
Рис. 4 Сравнение методов обнаружения сигнала.

 

На рис. 4а) для сеанса на трассе Норильск — Йошкар-Ола (500 кГц/с, 23.02.2010 г., 10:58 UTC) представлены сверху вниз: отметки на ионограмме сигнала, обнаруженного только критерием тестирования аномальных отсчетов, отметки сигнала, обнаруженного по представленному алгоритму, количество n отсчетов сигнала, выделенных в каждом спектре с порядковым номером m. Жирная линия соответствует первому способу выделения, тонкая — второму. Аналогично, на рис. 4б) представлены результаты для сеанса на трассе Lyon — Йошкар-Ола. Для первого сеанса алгоритм обнаружил на 80% больше отсчетов, для второго — на 60% больше, чем при простом использовании критерия.

Была проведена апробация на суточных циклах ЛЧМ-зондирования с шагом в один час для трасс Lyon — Йошкар-Ола (24 ионограммы, принятые 9.11.2009 г.) и Горьковская (Ленинградская обл.) — Йошкар-Ола (24 ионограммы, принятые 14.07.2011 г.). Для первой трассы было обнаружено отсчетов в среднем на 47% больше (минимум 22%, максимум 63%), чем при простом использовании критерия, для второй — на 30% (минимум 7%, максимум 60%). Оценочно число выделенных ложных отсчетов при использовании данного метода превышает число ложных отсчетов при простом использовании критериев обнаружения в 1,5-2 раза. Учитывая, что для критериев из [5] ошибка ложного обнаружения составляла не более 0,17% от общего числа фоновых отсчетов, то для представленного метода она составит не более 0,34%. При этом не происходит увеличения количества «ложных спектров», то есть элементов анализа, в которых обнаружен сигнал при его отсутствии. Связано это с тем, что второй этап обнаружения сигнала в описанном методе проводится только для элементов анализа, в которых уже выделены аномальные отсчеты.

5. Выводы

В работе представлен усовершенствованный метод обнаружения сигнала ЛЧМ-ионозонда в частотной области, базирующийся на выделении аномальных отсчетов и выделении отсчетов сигнала, входящих в уширение моды, обусловленное частотно-временной дисперсией и случайно-неоднородной структурой среды распространения сигнала. Разбиение процедуры на два этапа с эмпирической оценкой окрестности значимого (большего уровня шума на 8 дБ) уширения моды позволило избежать значительного увеличения числа ложных выделенных отсчетов при увеличении числа выделенных отсчетов сигнала в среднем на 30-40%.

 

Литература

 

1.    Вертоградов Г.Г., Урядов В.П., Вертоградов В.Г., Вертоградова Е.Г., Кубатко С.В., Валов В.А. Многофункциональный комплекс для наклонного зондирования на базе ионозонда-радиопеленгатора // Журнал радиоэлектроники: электронный журнал. 2010. № 12. URL: http://jre.cplire.ru/jre/dec10/4/text.pdf

2.    Иванов В.А., Иванов Д.В., Колчев А.А. Исследования особенностей дисперсионных характеристик радиоканалов с помощью ЛЧМ-ионозонда // Известия высших учебных заведений. Радиофизика. 2001. Т. 44. № 3. С. 241-254.

3.    Afanas'yev N.T., Grozov V.P., Nosov V.E., Tinin M.V. The Structure of a Chirp Signal in the Randomly Inhomogeneous Earth-Ionosphere Channel // Radiophysics and Quantum Electronics. 2000. Т. 43. № 11. С. 847-857.

4.    Колчев А.А., Щирый А.О., Недопекин А.Е. Математические модели и методики измерения АЧХ многолучевых ионосферных коротковолновых радиолиний. Йошкар-Ола, 2013. 147 с.

5.    Недопекин А.Е. Адаптация стандартных критериев тестирования статистических выбросов для выделения сигнала ЛЧМ-ионозонда // Журнал Радиоэлектроники: электронный журнал. 2013. № 9. URL: http://jre.cplire.ru/jre/sep13/5/text.pdf

6.    Колчев А.А., Шпак Д.Г. Исследование энергетических потерь при квазиоптимальной обработке ЛЧМ-сигнала // Фундаментальные проблемы радиоэлектронного приборостроения. 2009. Т. 9., № 4. С. 43-46.

7.    Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. Л.: Энергоатомиздат. Ленингр. отд-ние., 1991. 304 с.

8.    Колчев А.А., Недопекин А.Е., Шумаев В.В. Погрешности измерения доплеровского смещения частоты с помощью амплитудно-модулированного ЛЧМ-сигнала // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. 2010, № 4. С. 42-48.  

9.    Колесник С.Н., Тинин М.В., Афанасьев Н.Т. Имитационное моделирование распространения радиоволн в случайно-неоднородной ионосфере // Известия высших учебных заведений. Радиофизика. 2002. Т. 45., № 9. С. 731-745.