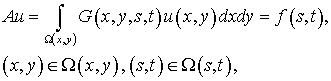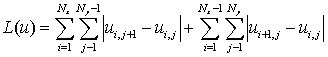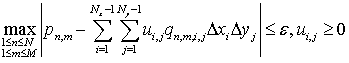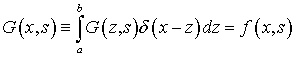УДК 520.622
Моделирование формирования изображения с субдифракционным разрешением на одномерной экспериментальной модели сканирующего одноапертурного терагерцового телескопа
А. Н. Выставкин1,3*, С. Е. Банков1,3, М. Е. Жуковский2,3, С. В. Подоляко2,3,
О. В. Корюкин1,*, Ю. Н. Казанцев1, А. Г. Коваленко1,*, Е. А. Выставкин 1,3,*,
А. С. Ильин2,*, .А. В. Уваров
2,*
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 Институт прикладной математики им. М.В. Келдыша РАН,
3ООО «Лаборатория терагерцовых радиометров» (резидент Инновационного центра "Сколково")
*Группа экспериментаторов Лаборатории терагерцовых сверхпроводниковых болометров ИРЭ им. В.А. Котельникова
Статья поступила в редакцию 9 октября 2015 г.
Аннотация. Предложен способ получения изображений с субдифракционным угловым разрешением с помощью сканирующего одноапертурного терагерцового телескопа. Описываются кратко схема телескопа и предлагаемый для процедуры сканирования и реконструкции изображения алгоритм. В статье поставлена простейшая задача моделирования формирования изображения с субдифракционным разрешением на одномерной экспериментальной модели сканирующего одноапертурного телескопа. Результатом моделирования явилась оценка возможности улучшения углового разрешения до ~ 140 раз. Предварительно намечены задачи, которые необходимо решить на пути создания одноапертурного двухмерного телескопа с формированием изображения с субдифракционным разрешением.
Ключевые слова: радиоастрономия терагерцового диапазона электромагнитного излучения, телескопы космические и наземные, способы улучшения характеристик телескопов, способы улучшения углового разрешения телескопов.
Abstract. A method of imaging formation with sub-diffraction angular resolution using a scanning one – aperture terahertz telescope was offered. We describe briefly the scheme of the telescope and the proposed algorithm for the procedure of scanning and reconstruction of images. The simplest problem of simulation of imaging formation with sub- diffraction resolution on one-dimensional experimental model of scanning one – aperture terahertz telescope has been put in the article. The estimation of the possibility of improvement of angular resolution up to ~ 140 times was the result of the simulation. Tasks which should be solved in the way of creating a one–aperture two-dimensional telescope with imaging formation with sub- diffraction resolution have been a prescheduled.
Keywords: radio astronomy of terahertz range, space and ground telescopes, methods of improvement of telescopes characteristics, angular resolution improvement.
Введение
Авторами патента на изобретение [1] предложен способ, позволяющий в значительной степени преодолеть дифракционные ограничения, а также шумовые и другие помехи в устройствах радиовидения (включая наземные и космические телескопы) миллиметрового, терагерцового и дальнего инфракрасного диапазонов электромагнитного излучения в задачах реконструкции изображений наблюдаемых объектов (распределения плотности источников). Акцент на перечисленных выше диапазонах электромагнитного излучения связан с интересами наблюдений вновь открытых в последние годы астрофизических особенностей микроволнового космического фона (см. Заключение), не более того. При применении упомянутого способа ожидаются достигаемые пространственное разрешение и четкость изображений распределений источников излучения значительно более высокими, чем у существующих устройств радиовидения указанных диапазонов в одноапертурном исполнении без применения названного выше способа (см. Заключение).
Схема упомянутого выше в названии статьи и тезисах сканирующего одноапертурного терагерцового телескопа в кратком изложении в одном из вариантов представляет собой следующее. Для достижения названных в предыдущем абзаце новых свойств телескопа предложено ввести в него конструктивные дополнения, а именно, слегка сдвинутое в сторону поперек от главной оптической оси вторичное зеркало по схеме Кассегрена для достижения некоторого переменного эксцентриситета и выполнения кругового сканирования изображения с этим эксцентриситетом относительно матрицы прямых приемных детекторов в фокальной плоскости телескопа (рис. 1).
Рис. 1. Схема сканирующего субдифракционного телескопа: 1- первичное зеркало оптической системы телескопа по схеме Кассегрена, 2 – вторичное зеркало: пунктир - исходное положение, сплошная линия - сдвинутое положение для осуществления сканирования, сплошные и пунктирные стрелки, ограничивающие сканируемый поток излучения, относятся к этим же положениям вторичного зеркала, 3 - блок с двумя шаговыми двигателями, осуществляющими сдвиг вторичного зеркала вбок от оси (штрих-пунктир) и вращение его по кругу относительно оси, 4 - матрица детекторов (например, сверхпроводниковых наноболометров, работающих на краю сверхпроводникового перехода [2]) в камере со сверхнизкой температурой (≤ 0,3 К), 5 – блок аналого-цифровых преобразователей и цифровых накопителей электрических сигналов pn,m и qn,m,i,j (об этих сигналах речь идет далее).
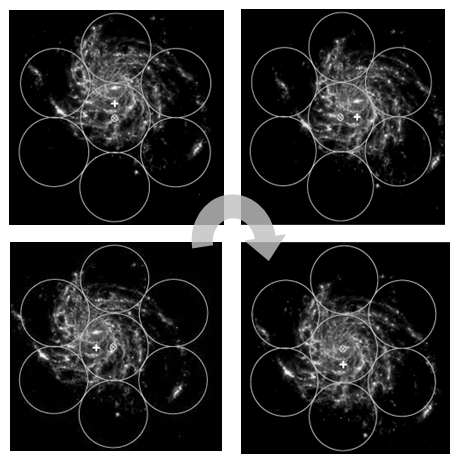
Рис. 2. Схема сканирования: изображение спиральной галактики М101 (с центром “белый крестик”) перемещается по кругу относительно матрицы из семи рупоров с детекторами с общим центром (на заднем плане). Белые окружности обозначают входы рупоров. Показано четыре положения при сканировании, на самом деле их много больше (>>100) с тем, чтобы обеспечить избыточность данных измерений над числом переменных в задаче. За n шагов одного кругового цикла сканирования при измерении электрических откликов на излучение от наблюдаемого объекта и от калибровочного источника с m детекторов приемной матрицы накапливается и заносится в память накопителей 5 (рис. 1) N×M значений pn,m откликов.
В качестве другого эквивалентного способа сканирования с эксцентриситетом, возможно применить известное К-зеркало [2]. Стратегия сканирования для обоих случаев представлена на рис. 2..Возможны другие способы сканирования с эксцентриситетом.
До отправки космической обсерватории с телескопом на орбиту или до начала (или после) наблюдений в случае наземного телескопа проводятся измерения аппаратной функции оптической системы телескопа. Главная составляющая этой аппаратной функции - дифракционные искажения. Для этих измерений в плоскости наблюдения источников вводится прямоугольная сетка (Рис. 3) с узлами в точках с координатами xi и yj. По всем узлам с помощью дополнительного приспособления перемещается отдельный точечный источник излучения и для каждого узла измеряются такие же отклики при сканировании, как в предыдущем случае. Обозначим их qn,m,i,j, где n и m - те же индексы, что и у откликов от изображения объекта, а i и j - индексы у координат узлов введенной прямоугольной сетки.
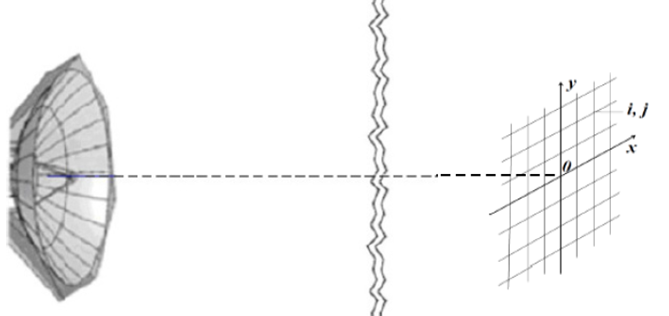
Рис. 3. Схема, поясняющая построение аппаратной функции оптической системы телескопа: слева - главное зеркало телескопа, справа – воображаемая прямоугольная сетка в плоскости источников излучения. Вторичные зеркала не показаны.
Наблюдаемое изображение восстанавливается в виде массива дискретных значений (пикселей) ui,j интенсивности изображения в узлах той же прямоугольной сетки с использованием данных всех описанных выше измерений при условии минимизации вариации интенсивности изображения L(u):
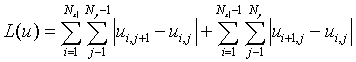(1)
при ограничениях
Функция распределения плотности
источников является решением системы интегральных уравнений первого рода [‡]). Соответствующая задача отыскания указанной функции
является некорректно поставленной. Неустойчивость таких задач и неточная
информация о входных данных требуют разработки т.н. регуляризирующих алгоритмов [3].
Требования к этим алгоритмам повышаются при рассмотрении задач, точные решения
которых являются функциями, обладающими сложной структурой (разрывы, угловые
точки и т.п.). Уточнить характер искомого решения позволяет использование
априорной информации различного типа[4-6].
Функция распределения плотности источников является, в общем случае, функцией, имеющей разномасштабную структуру, обусловленную различной яркостью и контрастностью изображений. Это обстоятельство порождает наличие особенностей в решении задачи (негладкость искомой функции).
Традиционные методы дают
«заглаживание» решения в окрестности особенностей искомой функции (размытие
решения), тем большее, чем больше погрешность входных данных 
(эта погрешность определяется искажениями
оптической системы, погрешностью измерительной системы, а также наличием шума
различного происхождения). Совокупное искажение искомого решения может быть
неприемлемым даже при не слишком больших уровнях погрешности входных данных .
Вместе с тем, в широком круге прикладных задач существует априорная информация о решении, использование которой при построении соответствующих методов может существенно улучшить качество приближенных решений [4,5]. Для этого следует при разработке регуляризирующего алгоритма использовать методы отбора приближений, обеспечивающих сходимость приближенного решения к точному решению вместе с производной на участках соответствующей гладкости. Реально, характер изменения кривой в данной точке определяется координатой и направлением касательной. Поэтому, приближая на гладких участках не только само решение, но и его производную, можно кардинальным образом повысить качество приближений [5].
В рассматриваемой работе исходная задача была определена как задача решения системы интегральных уравнений Фредгольма первого рода. Такие задачи являются некорректно поставленными и для их устойчивого решения были применены фундаментальные методы, разработанные в[4,5]. Применение этих методов при численном решении указанных уравнений дает возможность свести исходную бесконечномерную задачу к конечномерной задаче линейного программирования [6], которая решается методом последовательного улучшения решения, известного как модифицированный симплекс-метод[6,7]. С середины прошлого века этот метод с большим успехом применялся в основном для задач организационно-экономического типа. Начиная с 60-х г.г. прошлого столетия симплекс-метод “находил и находит сегодня уже успешное применение и для решения задач также в физике, химии, энергетике, геологии, биологии, механике и теории управления” [8]. Сюда же теперь следует добавить и радиовидение как раздел физики.
В данной статье
описываются разработанные методы решения задачи реконструкции функции
распределения плотности источников, а также результаты моделирования
предложенного способа формирования изображений с помощью экспериментальной
одномерной модели (имитатора) одноапертурного телескопа коротковолновой части
миллиметрового диапазона (
мм).
Методы решения рассматриваемых задач
Рассмотрим основные черты предлагаемых алгоритмов и их отличия от традиционных методов регуляризации.
Представим задачу в операторном виде:
|
(1) |
Здесь 
- интегральный
оператор 1-го рода, 
- правая часть (результаты измерений),
- искомое решение.
Если правая часть - известна не точно, а с некоторой погрешностью
(
, 
- норма в функциональном пространстве 
), то приближенные решения 
, такие, что 
могут
сколь угодно сильно отличаться друг от друга при сколь угодно малом 
Подавляющее большинство регуляризирующих алгоритмов решения задачи (1) традиционно основаны в том или ином виде [3,4] на минимизации функционала
|
(2) |
При этом, 
- т. н. стабилизатор, а 
- параметр регуляризации. Стабилизатор
вводится для того, чтобы обеспечить устойчивость получаемых приближений к малым
изменениям
поскольку решения задачи минимизации
функционала 
не обладают свойством устойчивости.
В соотношении (2) видна
причина указанного выше заглаживания (размытия) решения. Такое заглаживание
дает использование вполне непрерывного оператора в
функционале 
Для отыскания функции распределения источников в рассматриваемом проекте предлагается использовать идеи работ [4-6]. Основное отличие представленных в этих работах алгоритмов от традиционных методов заключается в том, что вместо (2) ставится вариационная задача отыскания минимума вариации искомого решения (и/или его производных):
|
(3) |
При этом, соотношение рассматривается как дополнительное
условие, наряду с другими условиями, следующими из априорной информации о
решении и записанными в виде линейных ограничений на искомое решение.
Вариация
функции характеризует дифференциальные свойства этой функции, а
дифференциальный оператор является неограниченным и, потому, может иметь
непрерывный обратный оператор, что дает возможность построения устойчивых
решений, сохраняющих свойства гладкости искомых функций. Решение задачи (3) не
требует введения «стабилизаторов» (можно доказать, что функционал 
сам является «стабилизатором»), а также
позволяет отказаться от понятия параметра регуляризации .
Предлагаемый метод решения состоит в следующем.
Рассмотрим интегральное уравнение
|
(4) |
соответствующее преобразованию
распределения плотности источников (искомой функции 
) в
измеряемую величину 
(изображение). В (4): 
- область определения ; 
-
область определения .
Пусть известна
погрешность эксперимента (в эту погрешность включаются
шумовые помехи, неточности измерительной аппаратуры и др.) такая, что 
. Здесь через 
обозначена
норма в пространстве функций 
.
В качестве искомой
функции рассматривается решение вариационной
задачи
|
(5) |
Здесь 
- вариация или ее
производных. Задача (5) решается при дополнительных ограничениях на искомую
функцию, которые следуют из априорной информации об этой функции. Например,
очевидным является требование неотрицательности решения 
.
Привлечение априорной информации уточняет характер искомого решения и в ряде случаев позволяет заметно повысить точность приближений. Поэтому, чем полнее в соответствующих методах учитывается имеющаяся априорная информация, тем, как правило, выше качество получаемых приближенных решений.
Таким, образом, алгоритм приближенного решения операторного уравнения (4) сводится к решению задачи (5) при дополнительных ограничениях, соответствующих априорной информации различного типа и записываемых в виде линейных условий (неравенств) на функционалы от искомой функции.
При численной реализации
предложенного метода реконструкции распределения плотности источников
проводится дискретизация двумерных областей 
и 
. В простейшем случае, когда в (5) обозначает вариацию функции , минимизируемый функционал на дискретной
области записывается в виде:
|
(6) |
Неравенство имеет смысл ограничений и вместе с требованием
неотрицательности искомого решения () выглядит следующим
образом:
|
(7) |
В формуле (7) введены
обозначения: 
; 
.
Таким образом, решение исходной задачи для уравнения (4) аппроксимируется решением дискретной задачи (6), (7).
Отметим в заключение этого раздела, что на практике вид аппаратной функции конкретного эксперимента, а именно, ядро уравнения (4), редко бывает известен с достаточной степенью точности. Поэтому в общем случае поиск искомого распределения источников по данным наблюдения сводится к решению двух задач:
1. определение функции отклика системы (ядро
уравнения (4) - 
) и
2. собственно, реконструкция функции распределения плотности источников.
Для решения первой из указанной задач применены подходы и алгоритмы, описанные в [9, 10]. Способы решения задачи (4) основаны, как уже указывалось, на применении идей работ [4-6].
Постановка одномерной задачи моделирования
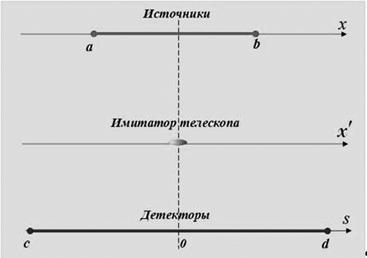
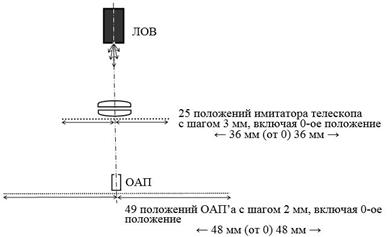
Обобщенная схема одномерного эксперимента представлена на рис. 4, а эскиз ее аппаратной реализации – на рис. 5.
Пусть искомая плотность распределения
источников излучения 
. Имитатор телескопа, точнее,
его центр, находится в точке 
(рис. 4).
Изображение 
формируется на линии детекторов 
.
Уравнение, связывающее плотность источников и их изображение на детекторной линии, записывается в виде:
|
(8) |
Таким образом, задача
отыскания функции 
сводится к решению интегрального
уравнения первого рода (8).
|
|
|
Рис. 4 – Схема одномерного эксперимента.
|
Следуя замечанию в конце
предыдущего раздела, необходимо вначале определить функцию 
. Ядро интегрального оператора в уравнении (8), имеющее смысл аппаратной
функции экспериментальной установки, определяется следующим образом [9]:
|
(9) |
Формально, соотношение (9)
определяет отклик «оптической» и измерительной системы (в нашем случае –
линейки детекторов) на точечный источник единичной мощности (то есть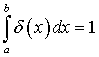 
).
Равенство (9) указывает
способ определения ядра интегрального уравнения (8), аппаратной функции
одномерного эксперимента. То есть, для того, чтобы построить , необходимо измерить сигнал 
в каждой точке 
от
дельта-источника излучения в каждой точке 
.
Важно отметить, что
функция (аппаратная функция эксперимента) определяется
как «оптической» системой, так и измерительным (регистрирующим) устройством.
Для численного решения
уравнения (8) необходимо провести дискретизацию задачи. Вводятся дискретные
сетки 
и 
. На
таких дискретных сетках тем или иным способом аппроксимируются плотность
источников (
) и показания детекторов (
), а также ядро 
уравнения
(8).
Значения функции 
в узловых точках двумерной области 
получаются путем измерения сигнала от
точечного источника, расположенного в точке 
,
детектором, находящимся в точке 
для всех значений 
. Значения функции в
промежуточных точках области 
можно получить,
например, с помощью билинейной интерполяции.
Дискретный аналог задачи (5) в одномерном случае записывается очевидным образом:
|
(10) |
с ограничениями:
|
(11) |
В
(11): 
; 
; 
.
Экспериментальная установка для получения изображения f(s)
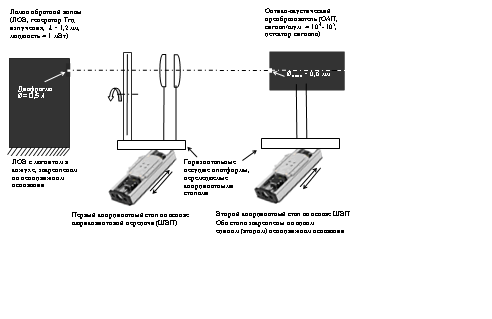
Эскиз экспериментальной установки представлен на рис. 5. Все компоненты установки верхнего ряда входят в состав и заимствованы из спектрометра миллиметрового/субмиллиметрового диапазона Института общей физики имени А. М. Прохорова РАН [11]. Координатные столы произведены и поставлены Компанией «НПФ Электропривод»[12]. Управление координатными столами и сбором данных осуществлялось с помощью универсального программного комплекса, разработанного в ИРЭ им. В.А.Котельникова РАН [13].
|
Рис. 5 – Эскиз экспериментальной установки. |
|
Выбранная схема перемещения имитатора телескопа относительно неподвижно закрепленной ЛОВ и перемещения ОАП’а относительно ЛОВ в каждом положении ЛОВ в горизонтальной плоскости вдоль линий, перпендикулярных оси квазиоптического тракта, в процессе измерений представлена на рис. 6.
|
|
|
|
Рис. 6 – Схема перемещения имитатора телескопа и ОАП’а
|
Очевидно, что описанная экспериментальная установка не дает прямой
возможности получить ядро уравнения , поскольку
в ней используется один источник и один детектор. Для имитации совокупности
источников реализован механизм перемещения имитатора телескопа, а для
имитации совокупности детекторов - механизм перемещения детектора (ОАП’а). Такой способ имеет ряд
преимуществ перед фактическим использованием нескольких источников и
нескольких детекторов. Очевидно, во-первых, что при указанном способе можно
достичь идентичности источников излучения и детекторов измерительной системы.
Во-вторых, такая схема эксперимента, безусловно, снижает расходы на требуемую
аппаратуру.
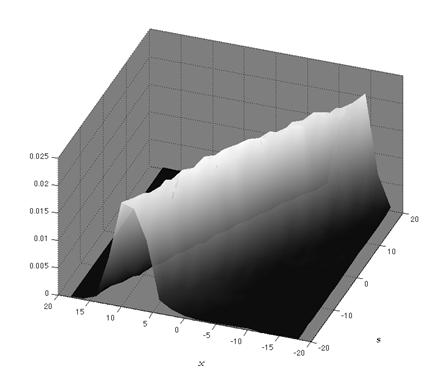
С помощью описанной
установки был проведен ряд очевидных измерительных процедур, результаты которых
дали возможность построить функцию отклика регистрирующей аппаратуры (ядро
уравнения ). Построенная графически функция изображена на рис. 7.
|
|
|
Рис. 7 – Функция |
Результаты моделирования
Для демонстрации возможностей разработанного метода реконструкции поля источников была проведена серия экспериментально-расчетных действий в рамках описанной выше одномерной модели.
В качестве аппаратной
функции использовалось построенное ядро
интегрального уравнения (8), изображенное на рис. 7. Поле источников задавалось
в виде двух точечных источников, расположенных на разных расстояниях друг от
друга в пределах дифракционного размытия их регистрируемого изображения.
Рассмотрим два примера моделирования.
Пример I. Суммарное излучение (сигнал) двух точечных источников, расположенных
в точках 
и 
,
фокусируется с помощью имитатора телескопа, располагаемого в точках на оси 
от 
до 
. После фокусировки интенсивность сигнала
измерялась с помощью детектора, последовательно располагаемого в точках на оси от 
до 
(рис. 6).
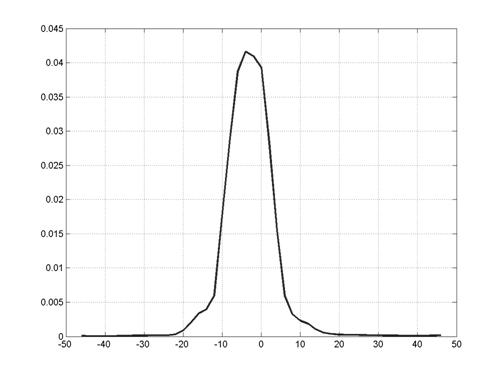
На рис. 8 представлен график зависимости интенсивности от положения детекторов при регистрации суммарного сигнала от двух точечных источников единичной интенсивности, расположенных в указанных выше точках. Погрешность измерений сигнала (включая шум) составила около 2% в равномерной сеточной метрике. То есть, максимальная величина отклонения составила 0.001.
|
|
|
Рис. 8. Изображение двух источников, полученное с помощью линейки детекторов. |
На рис. 9
приведен результат реконструкции положения и интенсивности источников
излучения, суммарный сигнал от которых изображен на рис.8. По оси абсцисс на
этих рисунках - расстояние в мм. На рис. 5 положение детекторов (линия на рис. 4). На рис. 6 - положение источников (линия 
на
рис. 4).
|
|
|
Рис. 9. Результат реконструкции положения и интенсивности двух источников (тонкие серые линии, спрятанные за толстыми и выступающие сверху, – точное решение), пример I. |
|
|
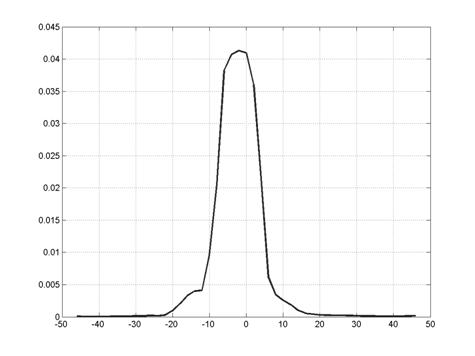
Рис. 10. Изображение двух источников, полученное с помощью линейки детекторов.
Пример II. На рис. 10 показан график интенсивности суммарного сигнала от двух точечных источников единичной интенсивности, расположенных на расстоянии 0.1 мм друг от друга. Погрешность эксперимента, как и в предыдущем случае (рис. 5), составила 2%.
На рис. 11 представлен результат реконструкции положения и интенсивности источников. По оси абсцисс на этих рисунках - расстояние также в мм.
Рис. 11. Результат реконструкции положения
и интенсивности двух источников
(тонкие серые линии, спрятанные за толстыми и
выступающие сверху, – точное решение), пример II.
Приведенные результаты показывают, что восстановление положения источников получается практически без погрешности. Ошибка определения интенсивности источников (заданные источники имеют единичную интенсивность) составила от 3% до 4%.
Отметим, что полуширина размытия изображения сигнала от двух источников в приведенных примерах (рис. 8 и рис. 10) составила примерно 12.5 мм.
Указанное размытие обусловлено дифракционными
эффектами и дефектами материала имитатора телескопа. В рассмотренных
экспериментах длина волны излучения составила λ
1,2мм.
Использовалась оптическая система из двух линз (имитатор телескопа) со
следующими параметрами: диаметр линз D = 50 мм, фокусное расстояние F = 120 мм. В этих условиях
размытие, обусловленное дифракцией (пятно Эйри), имеет характерную величину:
мм.
В приведенных примерах диаметр размытия около двух раз больше. Это обусловлено неоднородностями диэлектрического материала фокусирующей спаренной линзы, что приводит к рассеянию излучения и увеличению размытия.
Важно отметить, что разработанный способ расчета аппаратной функции спаренной линзы в эксперименте учитывает любые (в том числе перечисленные) дефекты и искажения, обусловленные как оптической системой, так и регистрирующей аппаратурой.
Определенный таким способом в рассматриваемом случае диаметр размытия аппаратной функции (14 мм) и принимается в качестве меры дифракционного ограничения углового разрешения конкретного устройства радиовидения, в нашем случае, имитатора телескопа при моделировании наблюдения им изображения из двух точек, разнесенных на расстояние 0,1 мм (во втором примере). Учитывая, что в описываемом случае моделирования формирования изображения с субдифракционным разрешением было достигнуто разрешение изображения из двух точек, разнесенных на расстояние 0,1 мм, мы определяем улучшение углового разрешения в 14: 0,1 = 140 раз. Поскольку все процедуры в данной работе выполнены на одномерной модели одноапертурного телескопа, мы расцениваем достижение улучшения углового разрешения как оценочный результат, стимулирующий проведение эксперимента по достижению субдифракционного разрешения на реальном телескопе (т.е. двухмерном) или на модели такого телескопа.
Замечание. Уровень погрешности в 2%, указанный в описании результатов расчетно-экспериментальных исследований, обусловлен шумовыми помехами и точностью использованной измерительной аппаратуры.
Исследование зависимости качества искомых распределений (количества источников, точность определения расстояния между ними, интенсивность источников) не входило в задачу данной работы. Главной целью проведенных исследований было установить принципиальную возможность преодоления дифракционных
ограничений при использовании одноапертурных телескопов терагерцового диапазона. Эта цель была достигнута. Исследование возможности преодоления шумовых и других ограничений целесообразно проводить в рамках того эксперимента, который соответствует реальной конструкции телескопа и реальным условиям проведения соответствующих экспериментов.
В результате проведенных исследований с одномерной моделью есть основания предполагать, что 5-типроцентный уровень погрешности (включая шум) не является критичным для наблюдений с субдифракционным разрешением.
Заключение
Достижение высокого углового разрешения у приборов радиовидения, в особенности у телескопов, и, в первую очередь, у космических телескопов, в терагерцовом диапазоне частот, в котором дифракционное ограничение углового разрешения, будучи пропорциональным рабочей длине волны, выражено гораздо сильнее, чем у коротковолновых приборов радиовидения, начиная с инфракрасного диапазона в сторону увеличения длины волны, представляет большой интерес после открытия ряда особенностей излучения космического фона в терагерцовом диапазоне частот и в ожидании на этой основе новых открытий [14, 15]. Подготовка к космическим миссиям дальнего инфракрасного и терагерцового диапазонов частот излучения идет полным ходом. Об этом свидетельствует перечень готовящихся миссий в разных странах: пример – перечень нескольких миссий НАСА США (Рис. 12) [16-20]. В России – это Космическая Миссия МИЛЛИМЕТРОН [21]. В этих программах придается большое значение как одноапертурным телескопам, так и интерферометрическим бинокулярным телескопам, угловое разрешение у которых (последних) существенно лучше, чем у одноапертурных телескопов (без применения изобретения [1]). Дело в том, что ожидается обнаружение весьма маломасштабным локальных особенностей космического фона, которые могут многое добавить к уже обнаруженным особенностям [14, 15]. В рамках программы “Космическая Миссия МИЛЛИМЕТРОН” сделано исключительно интересное предложение о реализации углового разрешения до нескольких наносекунд дуги с помощью бинокулярного интерферометрического телескопа “Космос-Земля”, когда составляющими этого телескопа являются собственно орбитальный телескоп “МИЛЛИМЕТРОН” и 68-апертурный наземный телескоп ”ALMA” на плато Чайнантор в Чили [22]. Для того, чтобы названный телескоп “Космос-Земля” работал более эффективно и производительно, авторам данной статьи представляется, что предлагаемый ими одноапертурный телескоп субдифракционного разрешения, САФИРсубдифр (см. рис. 12), или ему подобный, будет вполне кстати к применению для работы в связке с первым телескопом (интерферометрическим) для проведения предварительных обзорно-поисковых наблюдений с целью формирования-пополнения перечня объектов наблюдения для первого телескопа.
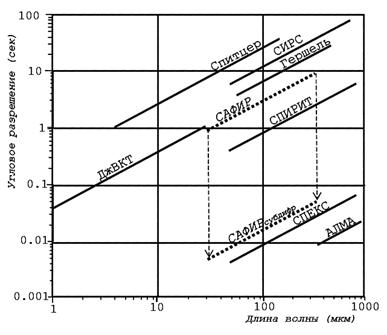
Рис. 12. Вновь планируемые в США во втором десятилетии 21-го века космические миссии дальнего ИК и ТГц диапазонов: космич. телескоп им. Дж. Вэбба[17], Космич. Миссия САФИР[18], два бинокулярных интерферометрических космич. телескопа СПИРИТ[19] и СПЕКС[20]. Частым пунктиром отображена зависимость углового разрешения одноапертурного телескопа Миссии САФИР до и после применения к нему способа формирования изображения с субдифракционным разрешением[1] при улучшении исходного разрешения в 140 раз, какое получено (оценка) при моделировании на одномерной модели, описанном выше. При этом, на долю второго телескопа можно будет взять вполне достаточно “работы” и по объектам “второго эшелона” (удовлетворяемых угловому разрешению ≈ < 0,01- 0,1сек), поскольку угловое разрешение такого телескопа на порядок, и даже чуть более чем на порядок лучше, чем у космического телескопа им. Дж. Вэбба (см. рис. 12) и подобным ему одноапертурным телескопам.
В свете всего сказанного, по мнению авторов статьи, заслуживает самого серьезного внимания одноапертурный телескоп, проведенное и описанное в предыдущих разделах исследование одномерной модели которого показало принципиальную возможность достижения углового разрешения до двух порядков с небольшим лучшего путем применения изобретенного способа формирования изображения с субдифракционным разрешением для таких телескопов [1]. Как это выглядит, показано на рис. 12 с телескопом САФИР. Следует подчеркнуть, что телескоп САФИРсубдифр обладает угловым разрешением на порядок лучшим, чем телескоп ДжВКТ (без применения обсуждаемого способа улучшения углового разрешения), хотя рабочий частотный диапазон у последнего и находится на порядок выше, чем у телескопа САФИРсубдифр!
Естественно, важно отметить, что полученные и описанные в предыдущем разделе результаты носят первый, предварительный характер и требуют дальнейших исследований, как в аппаратурном плане, так и в части алгоритмов реконструкции поля источников. Важно также сказать, что переход к реальным двумерным изображениям требует применения более сложных схемотехнических решений в терагерцовом диапазоне, а также разработки более сложных алгоритмов и более мощной (в том числе, гибридной) вычислительной техники. Второе, в частности, связано и с тем, что аппаратная функция в двумерном случае является функцией четырех переменных и для ее определения требуется очень большой объем вычислений. От всего сказанного в совокупности следует ожидать получения еще лучшего углового разрешения телескопа, хотя бы потому, что можно оптимизировать схемотехническое и алгоритмическое решения по большему числу параметров.
В заключение можно отметить, что изобретение с названием как в [1], по существу является также и изобретением нового телескопа, а именно, сканирующего одноапертурного телескопа терагерцового диапазона с субдифракционным разрешением. По крайней мере, авторам изобретения такой телескоп до сих пор был не известен. Не известен такой способ, а, следовательно, и такой телескоп, и экспертам Роспатента, что отмечено в отчете Роспатента о поиске [1].
Литература
1. Патент РФ № 2533502: А. Н. Выставкин, С. Е. Банков, М. Е. Жуковский, С. В. Подоляко, «Способ формирования изображения с субдифракционным разрешением», дата приоритета 20.02.2013, Бюллетень Роспатента № 32, 20.11.2014.
2. A.N. Vystavkin, A.G. Kovalenko, S.V. Shitov, S.E, Bankov, A.V. Pestryakov et al., Millimeter and Submillimeter Detectors and Instrumentation for Astronomy, Proc. of SPIE, Vol. 7020, P. 702024-1, 26-28 June 2008.
3. А.Н.Тихонов, В.Я. Арсенин Методы решения некорректно поставленных задач, М.: Наука. 1986.
4. В. П. Загонов, С. В. Подоляко, Некоторые алгоритмы приближенного решения интегральных уравнений первого рода при наличии априорных ограничений, Математическое Моделирование, 1992, Т.4, N 4, С. 89-100.
5. В. П. Загонов, Некоторые вариационные методы построения приближений негладких решений некорректно поставленных задач, ЖВМ и МФ, 1987, Т.27, №11, С.1614-1627.
6. В. П. Загонов, О приближении негладких решений некорректно поставленных задач в метрике Хаусдорфа, Препринт ИПМ им. М. В. Келдыша АН СССР, 1990, № 158.
7. Д. Б. Юдин, Е. Г. Гольштейн, Задачи и методы линейного программирования, Советское радио, Москва, 1961. Гл. 3 «Метод последовательного улучшения плана».
8. С.С. Кутателадзе, В.Л. Макаров, И.В. Романовский, Г.Ш. Рубинштейн, «Леонид Витальевич Канторович», Сибирский математический журнал, 2002, т. 43, № 1, с. 3-8, http://www.math.nsc.ru/LBRT/u2/nauka/kant.html.
9. Ю.А. Криксин, Численное решение интегральных уравнений первого рода мето-дом локальных невязок, Препринт ИПМ им. М.В.Келдыша АН СССР, 1986, №52.
10. M.E. Zhukovskiy, G.-R. Jaenisch, A. Deresch, S.V. Podoliako, Mathematical model-ing of radiography experiments. Beitrag zu einem Tagungsband, 18th WCNDT - World conference on nondestructive testing, Proceedings, 2012, Paper 305, 1-7 ISBN 978-0-20-52872-6.
11. Н.А. Ирисова, Метрика субмиллиметровых волн, Вестник АН СССР, 1968, в. 10, с. 63.
12. НПФ «Электропривод», http://www.eprivod.ru/index.htm
13. I. A.Cohn, A. G. Kovalenko and A. N. Vystavkin. "Experimental research control software system." In Journal of Physics: Conference Series, vol. 510, no. 1, p. 012004. IOP Publishing, 2014.
14. Дж. Ф. Смут, Нобелевская лекция, Анизотропия реликтового излучения: от-крытие и научное значение, Успехи физических наук, Декабрь 2007 г., Том 177, № 12.
15. Community Plan for Far-Infrared/Submillimeter Space Astronomy, paper representing the consensus view of the 124 participants in the “Second Workshop on New Con-cepts for Far-Infrared/Submillimeter Space Astronomy,” being held on 7 – 8 March 2002 in College Park, Maryland, issued by February 21, 2003.
16. D. Leisawitz, T. Armstrong, D.J. Benford et al., Probing the Invisible Universe: The Case for Far-IR / Submillimeter Interferimetry, (the same source).
17. J. P. Gardner, J. C. Mather, M. Clampin et al, The James Webb space telescope, Space Science Reviews, 2006, 123: 485–606, DOI: 10.1007/s11214-006-8315-7.
18. D.J. Benford, M.J. Amato, Mission concept for the single aperture far-infrared (SAFIR) observatory, Astrophysics and Space Science 2004, 294, 177–212.
19.David Leisawitz,, Charles Baker at al, The space infrared interferometric telescope (SPIRIT): High-resolution imaging and spectroscopy in the far-infrared, Advances in Space Research, 2007, 40, pp. 689–703.
20. D. Leisawitz, SPECS: The Kilometer-baseline Far-IR Interferometer in NASA's Space Science Roadmap, Optical, Infrared, and Millimeter Space Telescopes, Advances in Space Research, 2004, 34, pp. 631–636.
21. A.V. Smirnov, A.M. Baryshev, S.V. Pilipenko, N.V. Myshonkova, V.B. Bulanov, M.Y. Arkhipov, I.S. Vinogradov, S.F. Likhachev and N.S. Kardashev, Space mission Millimetron for terahertz astronomy, Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Proc. of SPIE, 2012, Vol. 8442, paper 84424C-1.
22. Н. С. Кардашев, “РАДИОАСТРОН” – Радиотелескоп много больше Земли. Научная программа, Успехи физических наук, Ноябрь 2009, Том 179, №11. (О программе “Миссия МИЛЛИМЕТРОН”, в части бинокулярного интерферометрического телескопа “Космос-Земля”, см. в [22], на стр. 1201-1202 и на рис. 17).