Usually frequency selective structures (FSS) are applied for frequency separation in dual frequency band antennas and for back scattering decreasing in radomes.

It is well known that gratings with conductive resonant elements of different shapes represent band-reflective FSSs [1-7]. At the resonant frequency, each element of the grating strongly scatters an incident wave, and therefore the grating reflects the wave completely. So, at the resonant frequency, the reflection coefficient is close to unity, and the transmission coefficient is close to zero.

Here we propose another method for the design and investigation of the band-reflective FSSs, when the grating is formed of both inductive and capacitive coupling elements in a conductive screen. For example, non-resonant round or square holes as well as sufficiently wide slots parallel to electric field serve as the inductive coupling elements. Narrow slots perpendicular to electric field represent the capacitive coupling elements. Note that the holes in the well-known pass-band FSSs [8-13] are resonant. Fig.1 shows some variants of investigated FSSs. Dark segments correspond to conductive parts and white segments correspond to slots and holes. The FSS shown in Fig.1a represents the array of mutually orthogonal narrow and wide slots cut in the thin conductive screen (or, which is the same, the two-dimensional array of metal rectangles). The FSS shown in Fig.1b represents an array of square holes and mutually orthogonal narrow slots cut in the thin conductive screen. The structures shown in Figs.1c and 1d are nearly the same as is in Fig1b, except the arrangement and the number of slots. In turn, the structures presented in Figs.1e and 1f differ from the structures 1b and 1d, respectively by the shape of the holes (round instead of square). The structure shown in Fig.1a operates at one incident wave polarisation when the electric field is parallel to the wide slots. The remaining structures can operate at two orthogonal polarisations.

The operation principles of these FSSs can be explained in the following way. The reflection and transmission coefficients for the structures under consideration may be written as

The term is due to the inductive coupling elements. It is positive and proportional to frequency. The term is due to the capacitive coupling elements. It is negative and inversely proportional to frequency. At certain frequency (rejection frequency), the terms and are cancelled mutually and the transmission coefficient vanishes, whereas the reflection coefficient tends to unity.

Note that some of the structures shown in Fig.1 do not differ from well-known resonance ones in their geometry.

The structures in Figs.1a, 1b and 1d may be considered as two-dimensional gratings with flat dipoles [3], square loops [7] and crossed dipoles [4] respectively. (A single grating element in Figs.1a, 1b and 1d is drawn in black.) The structures in Figs.1b and 1c may be considered as inverse gridded square or round elements arrays. The characteristic of the FSSs under consideration is the fact that the elements are located closely to each other and resonate collectively at frequency . The size of the elements may be substantially less than the rejection wavelength . It ensures the absence of the grating side lobes in the reflected field.

Note, all considered structures are total transmitting at the high frequency band due to eigen resonances of inductive coupling elements.

Previously the problem of scattering by a two-dimensional grating represented in Fig.1a was solved by numerical methods [3]. We obtain the approximate analytical solution when the grating periods do not exceed the wavelength and the grating elements are extended along the E-vector of the incident field. The inductive and capacitive terms of the transparency r are obtained in explicit form in the case of small (in comparison with l ) grating periods. We also give the expressions for evaluating the reflection and transmission coefficients of the FSSs shown in Figs.1b and 1e. We investigate experimentally all the variants of FSSs presented in Fig.1.

2. Two-dimensional grating with thin metal rectangles

Let a plane wave

be normally incident upon the two-dimensional grating with thin metal rectangles. The grating periods along the x and y-axes are 2A and 2B respectively; the rectangle dimensions are 2a and 2b (Fig.2). We assume at first, that the grating parameters satisfy the conditions

Due to the periodicity of the structure, it is sufficient to consider a problem within a single period of the structure . The incident field induces a surface current through the metal rectangle , which creates the scattered field . In view of we can neglect the x component of the current [3] and, consequently, x component of the electric field. In this approximation the electric Hertzian potential has only one component which satisfies the equation

    ,   .    (7)

The function represents the y component of surface current, which is nonzero only inside the metal rectangle

The electrical vector of the scattered field is expressed in terms of by the formula:

Its y component is given by

The tangential component of the total electric field satisfies the zero boundary condition on the metal surface:

     (10)

subject to the Neumann boundary conditions on the walls

In addition the function is assumed to satisfy the waveguide radiation condition; i.e. this function must not contain any waves incoming from infinity.

The functions , , and are related by the well-known formula [15]

Since is an even function of both co-ordinates, this formula can be rewritten as

  (14)

where is the even part of the function G.

The function can be represented as an expansion in terms of the waveguide eigen-functions:

  (15)

where

      (16)

Under conditions (5), the propagation constants of higher modes are imaginary, and we can use the approximation

(20)

The relation

    (22)

follows from (9) and (10).

Taking into account (14), we obtain from (22) the integro-differential equation for the current f(x, y):

  (23)

where

     (24)

The solution of the equation (23) is sought for the class of functions satisfying the following condition for the current on the rectangle edge [15]

      (25)

Reduction of the problem to a real equation

It follows from (23), (26), (27) that

    (28)

Using expression (1) for the reflection coefficient, we obtain from (21) and (28) that the grating transparency r is expressed in terms of the function g(x, y) as follows

      (29)

Taking into account (24), (15)-(19), the kernel of integro-differential equation (27) can be represented as

(30)

Here the symbol denotes that the term m=0 and n=0 is omitted in the sum.

Functions , satisfying condition (25) also satisfy the relation

  (31)

where

This relation is obtained in a usual way by changing the order of differentiation and integration (see, for example, [15]).

Taking into account (31), we rewrite equation (27) in the form 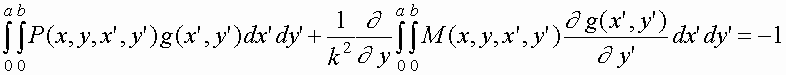. (33)

The kernels and of equation (33) are invariant under the permutation . Using this property we obtain the stationary representation

    (34)

When the condition is valid, it is appropriate to take a test function in the stationary functional (34) in the form of the product

Substitute the expressions (35) - (37) into the stationary representation (34). To calculate the integrals and the sums, we use the formulae

where are the Legendre polynomials.

As a result, we obtain the expression.

When or , this expression turns into the expression for the transparency r of a metal strip grating in the case of E or H-polarisation, respectively [14].

The transparency (46) contains the inductive and capacitive terms. At a certain frequency , when these terms are cancelled (i. e. ), the total reflection effect is observed.

This theory did not take into account the effect of dielectric substrate with permittivity e on which the metal rectangles are placed in a real grating. We can take into account this effect approximately by introducing the correction factor into the capacitive terms of expression (46):

(47)

This correction factor is advisable when dielectric substrate is present only on one side of the grating, the substrate thickness s is small in comparison with the wavelength in dielectric and large as compared to the narrow slots width .

In the derivation of expression (46), we take into account that the propagation constant (17) of the mode is real while the other modes are imaginary. For this to be true, it is sufficient that the grating parameters satisfy the conditions

instead (5). These conditions ensure the absence of grating side lobes in the scattered field. In this case, we cannot neglect the dependence on k of the kernels of the integro-differential equation (33):

(49)

(50)

Therefore the inductive and capacitive terms cannot be expressed in explicit form like in the expressions (46), (47). Instead of (47) we obtain the following series expansion for the transparency in terms of the Legendre polynomials:

(51)

It is supposed that Here, we have taken into account the correction factor .

Comparison of calculation results with experimental data

For the experimental verification of the theory, we prepared seven specimens of the grating shown in Fig.1a. These and all other specimens described below are made from a 12 m m thick aluminium foil deposited on 100 m m thick mylar () substrate. The basic dimensions and the rejection frequencies of the specimens are given in Table 1.

Table 1.

We will represent the experimental and calculated data by solid and dashed curves, respectively.

Figs.3-5 show the experimental and calculated results for specimens No 1, 3, 6 (see Table 1). The comparison of the experimental data with the theory shows that they are in a good agreement for specimens 1-5, i.e. up to values of .

Figs.6-8 display the calculated frequency dependences of the transmission and reflection coefficients for different parameters of the grating.

The rejection frequency band and the rejection frequency essentially depend on the grating period 2A (Fig.6). When the period 2A decreases and other parameters are constant, the rejection frequency band increases, and the rejection frequency also increases. The grating dimensions are indicated in the figure caption.

When the grating period 2A and the rectangle width 2a are changed simultaneously so that the width of the inductive coupling slots is constant, the rejection frequency is changed weakly, while the rejection frequency band is changed considerably (Fig.7).

When the grating period 2B and the rectangle length 2b are changed simultaneously so that the width of the capacitive coupling slots is constant, the rejection frequency band is changed weakly, while the rejection frequency is displaced considerably (Fig.8).

Fig.3. Transmission coefficient for specimen No 1 versus frequency.

Fig.4. Transmission coefficient for specimen No 3 versus frequency.

Fig.5. Transmission coefficient for specimen No 6 versus frequency.

Fig.6. Calculated transmission and reflection coefficients for structure 1a,

2A is variable, 2a = 0.2 cm, 2B = 1.2cm, 2b = 1.198 cm.

Fig.7. Calculated transmission and reflection coefficients for structure 1a,

2A and 2a are variable, 2b = 1.198 cm, 2B = 1.2cm, cm.

Fig.8. Calculated transmission and reflection coefficients for structure 1a,

2B and 2b are variable, 2a = 0.2 cm, 2A = 1.2cm, cm.

3. Other gratings

For investigating the frequency dependences of the transmission and reflection coefficients for all structures shown in Fig.1, we prepared six more specimens. Their basic dimensions are given in Table 2.

Table 2.

The results of measurements and theoretical estimations of these dependences are represented in Figs.9-14.

Fig.9. Transmission and reflection coefficients for specimen No 8 versus frequency.

Fig.10. Transmission and reflection coefficients for specimen No 9 versus frequency.

Fig.11. Measured transmission and reflection coefficients for specimen No 10 versus frequency.

Fig.12. Measured transmission and reflection coefficients for specimen No 11 versus frequency.

Fig.13. Transmission and reflection coefficients for specimen No 12 versus frequency.

Fig.14. Measured transmission and reflection coefficients for specimen No 13 versus frequency.

The solid curves in figures show the results of measurements, and the dashed curves in Figs. 9, 10, 13 display the results of theoretical estimates. Calculations for specimen No 8 was made by the formulae (1), (2) and (51). For specimens No 9 and 12, we made this estimate by the formulae (1), (2) and (3) under the assumption that the inductive and capacitive couplings are independent of each other. We calculated the value of from the expression for the transparency of the periodic array of square holes in metal screen [12]:

(52)

where c is the hole side, 2B is array period, , .

In the case of round holes, we used the same expression (52). As c we took the square side, whose area is equal to the area of the holes:

(53)

where d is the diameter of the holes.

For calculating the value of , we used the well-known expression for the transparency of metal strip grating given, for example, in [14]:

  (54)

where 2b is the strip width, 2B is the grating period. Here, we took into account the correction factor . The formula (54) is correct for gratings whose period is small as compared to the wavelength.

Note that the results of calculations and measurements do not conflict with each other, though the estimation is rather rough.

For frequencies , the transmission coefficients increase with frequency and virtually reach unity at a certain frequencies close to , where are the permittivity and permeability of the free space (Figs 9-14). One can see that the reflection coefficient at frequency is very small (from –18 down to ). This total transmission is due to the eigen resonance of the holes. Note, that the resonance at high frequencies is observed both for FSSs with holes (Figs 9-14) and for FSSs with inductive coupling slots (Figs 6, 8, 9). Such considered FSSs are characterised by both the rejection frequency band and the transmission frequency band. Recall that for frequencies (i.e. ) grating side lobes appear in the reflected and transmitted field.

4. Conclusion

The FSSs considered in this paper represent a thin metal screen with periodic holes and slots. Some of these holes and slots are inductive coupling elements and some are capacitive coupling elements. At the rejection frequency the inductive and capacitive coupling reciprocally compensate each other so that the transmission coefficient vanishes and the reflection coefficient tends to unity.

For the structures of comparatively simple geometry in the form of two-dimensional grating with thin extended metal rectangles (Fig.1a), we obtained analytical expressions for the reflection and transmission coefficients. If the grating periods are small in comparison with the wavelength, the expression for the transparency contain in explicit form the inductive (proportional to frequency) and capacitive (inversely proportional to the frequency) terms. Experimental verification of the theory has shown a good agreement between experimental and theoretical results for .

Experimental measurement of the FSSs properties of more complex structures (Fig.1b-f) showed that the transmission energy virtually vanishes () at the rejection frequency. Our rough theoretical estimation of transmission and reflection coefficients and experimental measurements for structures 1b and 1e are in a satisfactory agreement.

When choosing geometrical dimensions of the inductive and capacitive couplings elements, it is useful to keep in mind some common considerations. As the inductive or capacitive coupling increases, the rejection frequency band decreases. The rejection frequency decreases as the inductive coupling increases or increases as the capacitive coupling increases. When both inductive and capacitive couplings increase (decrease) simultaneously, the rejection frequency band decreases (increases), but the rejection frequency can change weakly.

References.

1. MITTRA R., CHAN C.H.: 'Techniques for analyzing frequency selective surface – a review', Proc. of the IEEE, 1988, vol. 76, pp. 1593-1614.
2. ORTA R., TASCONE R., ZICH R.: 'Frequency selective surfaces: spectral characterization and application to multifrequency antenna systems', Ann. Telecommun., 1985, vol. 40, pp. 378-386.
3. OTT R. H., KOUYOUMJIAN R. G., PETERS L., JR., 'Scattering by a Two-Dimension Periodic Array of Narrow Plates', Radio Science, 1967 vol. 2, pp. 1347-1359.
4. Pelton E.L., Munk B.A., 'Scattering from periodic arrays of crossed dipoles', IEEE Trans. on Antennas and Propagation, 1979, vol. AP-27, pp. 323-330.
5. Chen C.C., 'Scattering by a two-dimensional periodic array of conducting plates', IEEE Trans. on Antennas and Propagation, 1970, vol. AP-18, pp. 660-665.
6. Parker E.A., Hamdy S.M.A., 'Rinds as elements for frequency selective surface', Electron. Lett.,1981, vol. 17, pp. 612-614.
7. Langley R.J., Parker E.A., 'Equivalent circuit model for arrays of square loops', Electron. Lett.,1982, vol. 18, pp. 294-296.
8. Kieburtz R.B., Ishimaru A., Scattering by periodically apertured conducting screen', IEEE Trans. on Antennas and Propagation, 1961, vol. AP-9, pp. 506-514.
9. Chen C.C., 'Transmission through a conducting screen perforated periodically with apertures', IEEE Trans. Microw. Theory Tech., 1970, vol. MTT-18, pp. 627-632.
10. Chen C.C., 'Transmission of microwave trough perforated flat plates of finite thickness', IEEE Trans. Microw. Theory Tech., 1973, vol. MTT-21, pp. 1-6.
11. Mittra R., Hall R.C., Tsao G.H., 'Spectral-domain analyses of circular patch frequency selective surface', IEEE Trans. on Antennas and Propagation, 1984, vol. AP-32, pp. 533-536.
12. Lee S.W., Zarrillo G., Law C.L., 'Simple formulas for transmission through periodic metal grids or plates', IEEE Trans. on Antennas and Propagation, 1982, vol. AP-30, pp. 904-909.
13. Chen C.C., 'Diffraction of electromagnetic waves by a conducting screen perforated periodically with circular holes', IEEE Trans. Microw. Theory Tech., 1971, vol. MTT-19, pp. 475-481.
14. Electrodynamic Theory of Antennas with Translucent Surfaces: Methods of Constructive Synthesis', Editors: Katsenelenbaum B. Z. and Sivov A. N, Moscow, Nauka Press, 1989, (in Russian).
15. Hцnl H., Maue A. W., Westptahl K., in the 'Handbuch der Physik', Springer, Berlin, 1961, vol. 25/1.

Authors: