| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2001 |  |
ОПТИМИЗАЦИЯ УПРАВЛЕНИЯ МНОГОПОЗИЦИОННОЙ РЛС НА ОСНОВЕ ПРИМЕНЕНИЯ АППАРАТА СМЕШАННОГО РАСШИРЕНИЯ МАТРИЧНЫХ ИГР "НЕКЛАССИЧЕСКОГО" ТИПА
А. А. Строцев
Ростовский военный институт ракетных войск
Получена 9 августа 2001 г.
В статье рассмотрена задача поиска оптимального управления многопозиционной РЛС в условиях конфликта, в которой разыгрывание ситуаций предполагается ограниченное количество раз и ориентация на средний выигрыш за все партии не всегда обоснована. Для этой ситуации применяется аппарат смешанного расширения матричной игры "неклассического" типа.
Введение. Эффективность информационных подсистем, особенно в условиях конфликта, во многом определяет эффективность систем в целом. Из возможных вариантов построения этих подсистем в последнее время большое внимание уделяется многопозиционным РЛС (МПРЛС). Вопросам эффективности МПРЛС посвящено большое число работ и в качестве критериев эффективности чаще рассматриваются их собственные характеристики. При этом высокая эффективность может быть достигнута либо при их проектировании [1], [2], либо путём оптимизации алгоритмов их функционирования (оптимальное управление наблюдениями) [3] - [5]. Интересным направлением оценки эффективности МПРЛС является их оценка по критериям, характеризующим эффективность целой системы, в которой МПРЛС составляют информационную подсистему. Так, например, в [6] в качестве показателя эффективности радиолокационной системы, состоящей из 2 РЛС воздушного базирования, и входящей в состав ударного комплекса для уничтожения групповых наземных целей, принято относительное изменение потерь разведываемых объектов за время боевого эпизода. Следует отметить, что последний подход является наиболее продуктивным, поскольку учитывает влияние информационной подсистемы на выходной показатель эффективности всей системы.
Поскольку в этом случае рассмотрению подлежит вся система и, как правило, алгоритмы её функционирования, то сложность задачи определения показателей эффективности значительно возрастает, а вместе с ней усложняется и процесс поиска оптимального управления МПРЛС, особенно в условиях конфликтного противодействия. В общем случае для определения таких показателей эффективности при фиксированных стратегиях поведения противников необходимо разработать сложную систему математических моделей и методик, основанных на имитационном моделировании. В результате показатели эффективности отражают средние характеристики (в [6] - средние потери объектов вооружения и военной техники), опора на которые обоснована только при большом числе реализаций игровой ситуации. Последнее обстоятельство не всегда выполняется. Например, при выполнении особо важных заданий, невыполнение которых может повлечь серьёзные последствия, в большей степени важны оценки гарантированного характера, а не среднего результата.
Таким образом, определение оптимального управления МПРЛС по комплексным критериям, характеризующим эффективность всей системы, в условиях малого числа реализаций конфликтной ситуации, является актуальной задачей.
1. Постановка задачи. Рассматривается система вооружения, включающая в
качестве информационной подсистемы МПРЛС. Для этой системы задана
математическая модель, позволяющая для некоторого управления МПРЛС
![]() ,
,
![]() , где
, где
![]() - множество возможных вариантов
управления МПРЛС, значений случайных факторов
- множество возможных вариантов
управления МПРЛС, значений случайных факторов
![]() ,
,
![]() , учитываемых в модели, и некоторого
варианта действий противника
, учитываемых в модели, и некоторого
варианта действий противника
![]() ,
,
![]() , где
, где
![]() - множество возможных вариантов действий
противника, определить требуемый показатель эффективности системы (
- множество возможных вариантов действий
противника, определить требуемый показатель эффективности системы (![]() ), т.е. задан оператор
), т.е. задан оператор
Применение СВ носит конфликтный характер в отношении противника, при этом предполагается, что число реализаций игровой ситуации невелико.
Требуется в этих условиях построить модель игровой ситуации и найти оптимальные смешанные стратегии игроков.
2. Построение модели игровой ситуации. Поскольку число возможных стратегий противоборствующих
сторон полагается конечным (число вариантов управления МПРЛС равно
![]() , а число вариантов
действий противника -
, а число вариантов
действий противника -
![]() ),
то игровая ситуация может быть описана матрицей игры
),
то игровая ситуация может быть описана матрицей игры
![]() ,
,
![]() , с элементами
, с элементами
![]() ,
,
![]() ,
,
![]() . Ясно, что значения
. Ясно, что значения
![]() должны отражать
должны отражать
![]() и учитывать небольшое
число реализаций игровой ситуации. Поскольку
и учитывать небольшое
число реализаций игровой ситуации. Поскольку
![]() носит стохастический характер, то для
получения подходящих по смыслу решаемой задачи значений
носит стохастический характер, то для
получения подходящих по смыслу решаемой задачи значений
![]() можно воспользоваться, например,
методом имитационного моделирования [6] и получить статистический закон
распределения
можно воспользоваться, например,
методом имитационного моделирования [6] и получить статистический закон
распределения
![]() для
для
![]() ,
,
![]() ,
,
![]() ,
,
![]() , либо требуемые оценки числовых
характеристик.
, либо требуемые оценки числовых
характеристик.
Для единичных (или особо важных) применений системы
вооружения в качестве критерия оптимальности управления МПРЛС следует принять
критерий вероятностной гарантии
![]() с высокой вероятностью достижения
гарантированного результата [7]. При большом числе реализаций игровой ситуации
критерий оптимальности может отражать средние характеристики
с высокой вероятностью достижения
гарантированного результата [7]. При большом числе реализаций игровой ситуации
критерий оптимальности может отражать средние характеристики ![]() . В частности, в [6] в качестве
выходного показателя эффективности радиолокационной системы принято
относительное изменение потерь разведываемых объектов за время рассматриваемого
боевого эпизода, рассчитываемое на основе средних потерь.
. В частности, в [6] в качестве
выходного показателя эффективности радиолокационной системы принято
относительное изменение потерь разведываемых объектов за время рассматриваемого
боевого эпизода, рассчитываемое на основе средних потерь.
Однако для условий рассматриваемой задачи требуется
взвешенная позиция, для получения которой воспользуемся методом суперкритерия с
аддитивным включением частных критериев
![]() и
и
![]() [7]:
[7]:
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() - нормирующие коэффициенты, а
- нормирующие коэффициенты, а
![]() - весовой коэффициент,
- весовой коэффициент,
![]() .
.
Таким образом, в зависимости от значения
![]() элементы матрицы игры
элементы матрицы игры
![]() будут выражать, либо
большую склонность лица, принимающего решение (ЛПР) к получению гарантированного
результата (при малом числе реализаций игры), либо к максимальному среднему
выигрышу за большое число реализаций игры.
будут выражать, либо
большую склонность лица, принимающего решение (ЛПР) к получению гарантированного
результата (при малом числе реализаций игры), либо к максимальному среднему
выигрышу за большое число реализаций игры.
Модели матричных игр хорошо изучены и представлены
традиционными матричной игрой в "чистых стратегиях" и смешанным
расширением матричной игры. При этом оптимальная стратегия в матричной игре при
наличии седловой точки в чистых стратегиях совпадает со стратегией оптимальной
по минимаксному (ММ) или максиминному критерию для каждого из игроков. В
смешанном расширении матричной игры стратегии игроков, принадлежащие спектру
(а следовательно, реализуемые в процессе разыгрывания) оптимальны для
каждого из игроков относительно критерия Байеса-Лапласа (критерий BL). Однако эти модели в условиях решаемой задачи не
применимы, т.к. нет оснований полагать, что матрица игры в общем случае имеет
хотя бы одну седловую точку в чистых стратегиях, а критерий Байеса-Лапласа
хорошо согласуется только с опорой ЛПР на средний результат за большое число
реализаций игровой ситуации. В [8], [9] показана возможность построения модели
конфликта в виде смешанного расширения матричной игры
"неклассического" типа, которая отличается более гибким подходом к
учёту интересов ЛПР. Так, в [8] построена модель смешанного расширения
матричной игры "неклассического типа", использующая критерий Ходжа-Лемана
(критерий HL) с параметром
![]() . Для этой модели при предельных
значениях
. Для этой модели при предельных
значениях
![]() (
(![]() =1,
=1,
![]() =0) модель предпочтения ЛПР
соответствует или критерию BL, или MM-критерию.
Выбор промежуточного значения параметра
=0) модель предпочтения ЛПР
соответствует или критерию BL, или MM-критерию.
Выбор промежуточного значения параметра
![]() обеспечивает ориентацию как на средний
результат, так и на получение наилучшего гарантированного результата в
соотношении, связанном со значением
обеспечивает ориентацию как на средний
результат, так и на получение наилучшего гарантированного результата в
соотношении, связанном со значением
![]() . Поскольку такая модель игровой ситуации в
полной мере соответствует поставленной задаче, рассмотрим её построение.
. Поскольку такая модель игровой ситуации в
полной мере соответствует поставленной задаче, рассмотрим её построение.
Определим множества
![]() и
и
![]() , являющиеся множествами смешанных
стратегий
, являющиеся множествами смешанных
стратегий
![]() ,
,
![]() , соответственно, для
первого и второго игроков, т.е.
, соответственно, для
первого и второго игроков, т.е.
![]() ,
,
![]() и
и
![]() ,
,
![]() таковы, что
таковы, что
В качестве первого игрока определим ЛПР (сторону применяющую систему вооружения), а под вторым игроком будем понимать противника. В этом случае в соответствии с [8] функция выигрыша первого игрока, которую второй игрок стремиться минимизировать, может быть представлена в виде
Тогда в качестве смешанного расширения матричной игры "неклассического"
типа, основанного на использовании критерия Ходжа-Лемана с параметром b вторым игроком (т.е. критерия
![]() ), определим тройку вида
), определим тройку вида
Отметим, что при
![]() = 1 имеем
= 1 имеем
![]() , где
, где
![]() - смешанное расширение матричной игры "классического"
типа, а
- смешанное расширение матричной игры "классического"
типа, а
![]() -
функцию выигрыша первого игрока в этой модели игры,
-
функцию выигрыша первого игрока в этой модели игры,
С учётом (2) выражение (4) принимает вид
В тех случаях, когда нет необходимости учитывать
средние характеристики в элементах матрицы игры, т.е. при
![]() , выражение (7) совпадает с
функцией выигрыша рассмотренного в [8] смешанного расширения матричной игры
"неклассического" типа.
, выражение (7) совпадает с
функцией выигрыша рассмотренного в [8] смешанного расширения матричной игры
"неклассического" типа.
3. Алгоритм поиска оптимального управления МПРЛС по
комплексному критерию. В соответствии с постановкой задачи и моделью игровой
ситуации, описываемой игрой вида
![]() с функцией выигрыша (7), алгоритм поиска
оптимального управления МПРЛС по комплексному критерию можно представить в
следующем виде:
с функцией выигрыша (7), алгоритм поиска
оптимального управления МПРЛС по комплексному критерию можно представить в
следующем виде:
1.
На основе (1) с использованием (2) строится матрица игры. При этом ЛПР исходя
из числа реализаций игровой ситуации определяет весовой коэффициент
![]() . Нормирующие
коэффициенты
. Нормирующие
коэффициенты
![]() и
и
![]() определяются
в соответствии с требованиями метода суперкритерия [7].
определяются
в соответствии с требованиями метода суперкритерия [7].
2.
Для формирования игры
![]() ЛПР для своей модели предпочтения, учитывая
число реализаций игровой ситуации, определяет значение параметра
ЛПР для своей модели предпочтения, учитывая
число реализаций игровой ситуации, определяет значение параметра
![]() .
.
3. Для определения оптимальной смешанной стратегии строятся и решаются двойственные задачи линейного программирования вида [8]:
найти
при ограничениях
![]() ,
,
![]() ; (9)
; (9)
найти
при ограничениях
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() - векторы, соответствующей размерности,
каждая компонента которых равна единице,
- векторы, соответствующей размерности,
каждая компонента которых равна единице,
![]() - вектор-столбец с компонентами
- вектор-столбец с компонентами
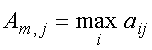 .
.
4.
Нахождение оптимальных смешанных стратегий
![]() ,
,![]() и значения игры
и значения игры
![]() осуществляется по выражениям:
осуществляется по выражениям:
где
![]() ,
,
![]() ,
,![]() ,
,
![]() - решения задач (8), (9) и (10), (11).
- решения задач (8), (9) и (10), (11).
4. Пример оптимизации управления МПРЛС по комплексному критерию на
основе построения игры ![]() .
.
Рассмотрим систему вооружения, описанную в [6]. Она включает МПРЛС воздушного базирования для обнаружения групповых наземных целей и системы высокоточного оружия. В качестве возможных вариантов действий противника рассматриваются возможности применения средств снижения заметности обнаруживаемых целей, средств активного радио (оптико) - электронного подавления, средств противовоздушной обороны.
Множество стратегий ЛПР может быть сформировано путём применения различных способов применения РЛС.
Пусть в условиях примера
![]() , число реализаций игровой ситуации не
велико и задана методика комплексной оценки эффективности МПРЛС в условиях
конфликтного противодействия [6]. В качестве показателя эффективности системы
(1) примем число поражённых целей.
, число реализаций игровой ситуации не
велико и задана методика комплексной оценки эффективности МПРЛС в условиях
конфликтного противодействия [6]. В качестве показателя эффективности системы
(1) примем число поражённых целей.
Требуется определить оптимальные смешанные стратегии игроков в конфликтной ситуации.
Для решения поставленной задачи построим ей
соответствующую игру вида
![]() .
.
При формировании матрицы игры (п.1 алгоритма) положим, что в условиях примера:
![]() - среднее число поражённых одиночных целей
из состава групповой за время типового боевого эпизода при i-й
чистой стратегии ЛПР и j-й чистой стратегии
противника;
- среднее число поражённых одиночных целей
из состава групповой за время типового боевого эпизода при i-й
чистой стратегии ЛПР и j-й чистой стратегии
противника;
![]() - число поражённых с вероятностью
- число поражённых с вероятностью
![]() одиночных целей из
состава групповой за время типового боевого эпизода при i-й
чистой стратегии ЛПР и j-й чистой стратегии
противника;
одиночных целей из
состава групповой за время типового боевого эпизода при i-й
чистой стратегии ЛПР и j-й чистой стратегии
противника;
![]() - число одиночных целей в составе групповой
(
- число одиночных целей в составе групповой
(![]() );
);
Пусть в соответствии с методикой [6] определены
вероятности ![]() поражения
одиночной цели из состава групповой за время типового боевого эпизода при i-й чистой стратегии ЛПР и j-й
чистой стратегии противника:
поражения
одиночной цели из состава групповой за время типового боевого эпизода при i-й чистой стратегии ЛПР и j-й
чистой стратегии противника:
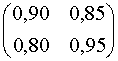 .
.
Тогда на основе выражений
где
 ,
,
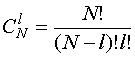 ,
,
![]() -множество целых чисел,
-множество целых чисел,
получим:
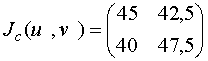 ,
,
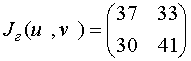 .
.
С учётом выражения (2) и значений (13) параметров суперкритерия матрицу
игры
![]() можно
представить в следующем виде
можно
представить в следующем виде
Для анализа решения задачи положим
![]() Кроме решения
матричной игры, т.е. кроме значений
Кроме решения
матричной игры, т.е. кроме значений
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , определим для первого игрока вероятность
получения им в любой из партий выигрыша
, определим для первого игрока вероятность
получения им в любой из партий выигрыша
![]() не меньшего максимального
гарантированного:
не меньшего максимального
гарантированного:
![]() ,
а для второго игрока - вероятность получения им в любой из партий проигрыша не
большего минимального гарантированного:
,
а для второго игрока - вероятность получения им в любой из партий проигрыша не
большего минимального гарантированного:
![]() . Для рассматриваемых исходных данных
. Для рассматриваемых исходных данных
![]() , а
, а
![]() . Результаты решения
задач (8)-(11), (17) с использованием (12) приведены в табл. 1.
. Результаты решения
задач (8)-(11), (17) с использованием (12) приведены в табл. 1.
Таблица 1.
Результаты решения игры
|
Рассчитываемая величина |
|
|
|
|
|
|
1,0000 |
1,0000 |
0,8238 |
0,7357 |
|
|
0 |
0 |
0,1762 |
0,2643 |
|
|
1,0000 |
0,7381 |
0,5286 |
0,5286 |
|
|
0 |
0,2619 |
0,4714 |
0,4714 |
|
|
0,7720 |
0,7720 |
0,7546 |
0,7371 |
|
|
1,0000 |
1,0000 |
0,9069 |
0,8603 |
|
|
1,0000 |
1,0000 |
0,9169 |
0,8754 |
Из анализа данных таблицы следует, что при
![]() и
и
![]() второй игрок гарантированно (с
вероятностью равной единице) получает в любой отдельной партии проигрыш не
превышающий проигрыш, соответствующий его минимаксной стратегии, а первый игрок
также гарантированно (с вероятностью равной единице) получает в любой отдельной
партии выигрыш не меньший выигрыша, соответствующего его максиминной стратегии
(так же как и в игре с матрицей А при наличии седловой точки в чистых стратегиях). С
ростом значения
второй игрок гарантированно (с
вероятностью равной единице) получает в любой отдельной партии проигрыш не
превышающий проигрыш, соответствующий его минимаксной стратегии, а первый игрок
также гарантированно (с вероятностью равной единице) получает в любой отдельной
партии выигрыш не меньший выигрыша, соответствующего его максиминной стратегии
(так же как и в игре с матрицей А при наличии седловой точки в чистых стратегиях). С
ростом значения
![]() вероятности
получения гарантированных результатов уменьшаются, а средний проигрыш второго
игрока уменьшается и при
вероятности
получения гарантированных результатов уменьшаются, а средний проигрыш второго
игрока уменьшается и при
![]() результаты решения игры
результаты решения игры
![]() совпадают с
результатами игры
совпадают с
результатами игры
![]() .
Ясно, что при малом числе разыгрываний предпочтение игроков должно быть смещено
в сторону гарантированных результатов. При увеличении числа разыгрываний предпочтение
второго игрока может быть смещено в сторону уменьшения среднего проигрыша.
Таким образом, применение модели матричной игры "неклассического"
типа позволяет провести оптимизацию управления МПРЛС на основе гибкого учёта в
моделях предпочтения игроков фактора числа реально проводимых разыгрываний.
.
Ясно, что при малом числе разыгрываний предпочтение игроков должно быть смещено
в сторону гарантированных результатов. При увеличении числа разыгрываний предпочтение
второго игрока может быть смещено в сторону уменьшения среднего проигрыша.
Таким образом, применение модели матричной игры "неклассического"
типа позволяет провести оптимизацию управления МПРЛС на основе гибкого учёта в
моделях предпочтения игроков фактора числа реально проводимых разыгрываний.
Заключение. В статье рассмотрено применение аппарата смешанного расширения матричных игр "неклассического" типа для решения задачи оптимизации управления МПРЛС в условиях конечного числа возможных стратегий противоборствующих сторон. Показано, что применение этого аппарата расширяет возможности учёта предпочтений игроков.
СПИСОК ЛИТЕРАТУРЫ
1. Черняк В.С. Многопозиционная радиолокация. М.: Радио и связь, 1993.
2. Кондратьев В.С., Котов А.Ф., Марков М.Н. Многопозиционные радиотехнические системы / Под ред. В.В. Цветанова. М.: Радио и связь, 1986.
3. Хуторцев В.В. Оптимальное управление наблюдениями в комплексных информационных системах. МО РФ, 1993.
4. Хуторцев В.В. Оптимальное планирование измерительных средств в многопозиционных радиосистемах со стохастической структурой каналов наблюдения / Радиотехника и электроника, 1991, т.36, №6.
5. Хуторцев В.В., Строцев А.А. Инвариантно-групповые принципы оптимизации наблюдений многоканальной импульсной РЛС в составе многопозиционной комплексной измерительной системы / Радиотехника и электроника, 1992, т.37, №6, с.63-70.
6. Керков В.Г. Скабаров М.М. Методика комплексной оценки эффективности радиолокационной системой в условиях конфликного противодействия. – Интернет-публикация, М.: Журнал радиоэлектроники , №12, 2000.
7. Мушик Э., Мюллер П. Методы принятия технических решений. М.: Мир, 1990.
8. Строцев А.А. Построение смешанного расширения матричной игры "неклассического" типа / Изв.АН. Теория и системы управления, 1998, №3.
9. Строцев А.А. Модифицированный метод Бауна решения смешанного расширения матричной игры "неклассического" типа / Экономика и математические методы, 2001, № 2.
Автор:
Строцев Андрей Анатольевич, кандидат
технических наук,
доцент кафедры Ростовского военного института ракетных войск
e-mail: apl@aaanet.ru
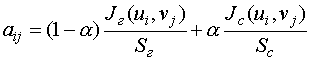 , (2)
, (2)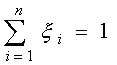 ,
,
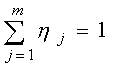 . (3)
. (3)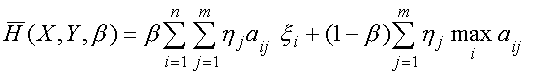 (4)
(4)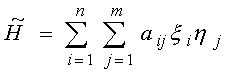 .
(6)
.
(6)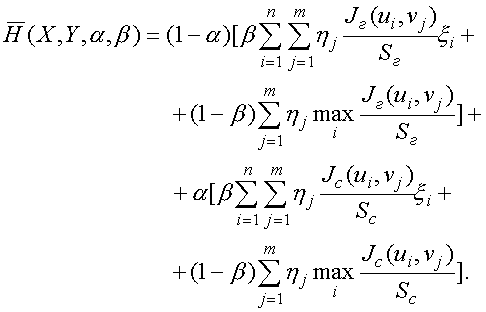 (7)
(7) ,
(8)
,
(8) ,
,  ,
(10)
,
(10)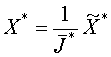 ,
,
 ,
,
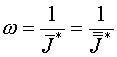 ,
(12)
,
(12)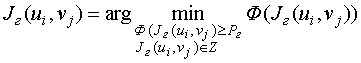 ,
(15)
,
(15)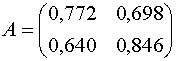 .
(17)
.
(17)