ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ОСЕСИММЕТРИЧНЫХ ДВУХЗЕРКАЛЬНЫХ
АПЛАНАТИЧЕСКИХ АНТЕНН
 

А.Г. Давыдов, В.А.Калошин , Е.В. Фролова,

Институт радиотехники и электроники РАН

 

Получена 15 сентября 2005 г.

 

Приводятся результаты исследования  характеристик осесимметричных аплантических двухзеркальных антенн на основе схем Кассегрена и Грегори. Проведен анализ зависимости формы зеркал, КИПа и диаграмм направленности от геометрических параметров системы, ширины диаграммы направленности облучателя и угла отклонения луча. Основной анализ выполнен с учетом трех последовательных  дифракций поля облучателя на вспомогательном и главном зеркалах в приближении Кирхгофа, что позволило учесть эффект затенения излучения вспомогательным зеркалом. Характеристики излучения приближенной модели как для  реального облучателя (гофрированного рупора), так и для всей системы при центральном положении луча, сопоставлены с результатами строгого расчета, полученного на основе метода интегрального уравнения.

 

Введение

 

         Двухзеркальная осесимметричная апланатическая система  типа Кассегрена с фокусировкой в дальней зоне впервые, по-видимому, была исследована в работе [1], в связи с чем, ее часто называют системой Шварцшильда. Несмотря на существенное уменьшение аберраций при отклонении луча апланатической антенны при смещении облучателя из фокуса по сравнению с классическими двухзеркальными системами Грегори и Кассегрена, апланатические антенны не получили до настоящего времени широкого применения. Как отмечено в [2], число работ, посвященных исследованию характеристик апланатических антенн, также невелико. Однако в последнее время интерес к таким антеннам возрос в связи с их возможностями формирования многолучевых диаграмм направленности в широкой полосе частот. Целью данной работы является исследование характеристик двухзеркальных осесимметричных апланатических антенн типа Кассегрена и Грегори в зависимости от их геометрических параметров, ширины диаграммы направленности облучателя и угла отклонения луча. 

                       

 

1.Синтез образующих апланатической системы.

 

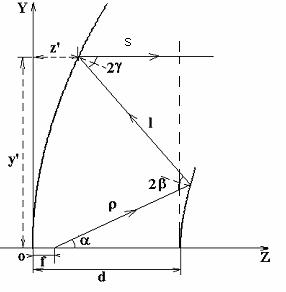
         Поместим начало координат в вершину главного зеркала (см. рис.1), а источник излучения в фокус системы на расстоянии f от начала координат. На рисунке обозначено:

d - расстояние между главным и вспомогательным зеркалом на оси системы,

f – расстояние между источником и главным зеркалом (фокальный отрезок),

z¢,y¢ –декартовые координаты образующей главного зеркала в плоскости ZY,

r(a) – радиус-вектор образующей вспомогательного зеркала.

Чтобы обеспечить синфазность поля в апертуре антенны, необходимо, чтобы все лучи, отраженные от главного зеркала, были параллельны оси системы. Для обеспечения отсутствия аберраций, пропорциональных первой степени смещения облучателя из фокуса,  функция отображения выходящего из облучателя лучевого фронта и фронта в апертуре главного зеркала должна удовлетворять условию синусов Аббе: y¢=, где - фокальный радиус апланатической системы.

 

 

а)                                                                      б)

 

Рис.1

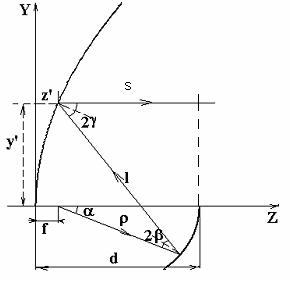
Геометрические схемы к расчету образующих двухзеркальных

апланатических антенн типа  Кассегрена (а) и Грегори (б).

 

 

При заданных условиях для схем, изображенных на рисунке 1, можно получить [2] следующую систему уравнений

 

      1)    ;

     2)    ;

      3)    ;                                                                                               

      4)    ;

                                                                                                   (1)

      5)    ;

      6) ;

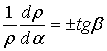где знак «+»  относится к схеме Кассегрена (рис.1а), а знак «-» к схеме Грегори (рис.1б).

Решение системы (1) для радиуса-вектора образующей вспомогательного зеркала и декартовых координат образующих главного зеркала имеет вид

 

  

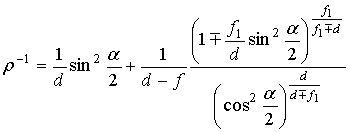
 (2)

                                                             

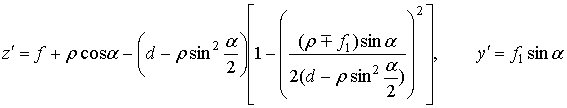
Y¢=, где  -угловой размер вспомогательного зеркала.

         В осесимметричной антенне поверхности зеркал образуются вращением апланатических образующих, которые описываются формулами (2), относительно оси Z. Отметим, что полученные формулы отличаются от приведенных в [2].

 

2.Моделирование источника излучения.

        

         При  решении задачи последовательной дифракции волны на  поверхностях главного и вспомогательного зеркал методом Кирхгофа в качестве модели облучателя использовалась круглая плоская апертура радиуса   с распределением вертикальной составляющей электрического поля Еy в виде функции Бесселя 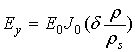, где d= 2,4048 . Заданная аппроксимация распределения поля обеспечивает ширину диаграммы направленности в дальней зоне на уровне 10дБ 60° и в пределах этого углового сектора достаточно хорошо моделирует реальный облучатель в виде гофрированного рупора (рис.2).

 

 

Рис.2

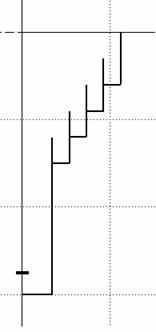
Образующая рупора с продольным гофром.

 

Нормированные диаграммы направленности гофрированного рупора, расчитанные на основе метода интегральных уравнений (ИУ) и его апертурной модели в вертикальной и горизонтальной плоскостях приведены на рис.3.

 

Рис.3

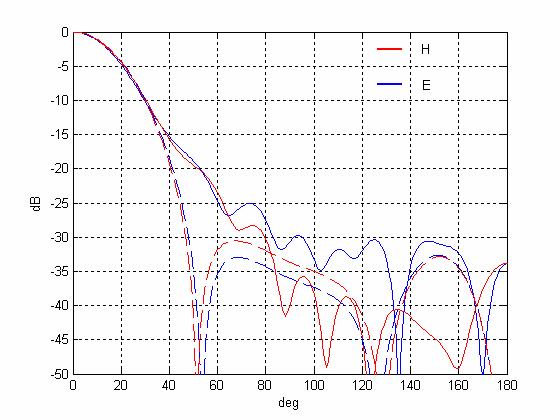
Диаграммы направленности облучателя.

 

Красные кривые - в Н плоскости, синие - в Е плоскости, сплошные кривые – моделирование методом ИУ для гофрированного рупора, пунктирные кривые – диаграммы эквивалентной плоской апертуры .

         Из рисунка видно, что апертурная модель в секторе углов ±30° хорошо описывает диаграмму направленности реального рупорного облучателя.

 

 

3.Моделирование диаграммы направленности  двухзеркальной

апланатической антенны типа Грегори двумя методами.

 

В осесимметричных  двухзеркальных системах необходимо учитывать эффект затенения излучения вспомогательным зеркалом. Для оценки этого эффекта  и других эффектов, которые не учитываются приближением Кирхгофа, диаграммы направленности апланатической антенны типа Грегори вычислялись двумя методами: методом ИУ и методом Кирхгофа. Причем решение методом ИУ было получено как для сплошного главного зеркала, так и для случая  главного зеркала с центральным отверстием с радиусом, равным радиусу апертуры вспомогательного зеркала.

 

         На рисунках 4-5 представлены диаграммы направленности (зависимости коэффициента усиления G от угла наблюдения)  двухзеркального апланата типа Грегори  в вертикальной (рис.4) и горизонтальной (рис.5) плоскостях.

Синий цвет кривых – метод Кирхгофа (сплошные кривые – с учетом затенения, штриховые – без учета ), зеленый – метод ИУ для сплошного главного зеркала, красный – метод ИУ для зеркала с отверстием.

         Расчеты проведены для следующих параметров системы: расстояние между главным и вспомогательным зеркалом d=1,02м, расстояние между источником и главным зеркалом f=0,12м, угловой размер вспомогательного зеркала 2α_max=60°,  фокальный радиус апланатической системы f₁=2, размер апертуры главного зеркала y^'_max=1м (отношение диаметра к длине волны D/l=100).

 

Рис. 4

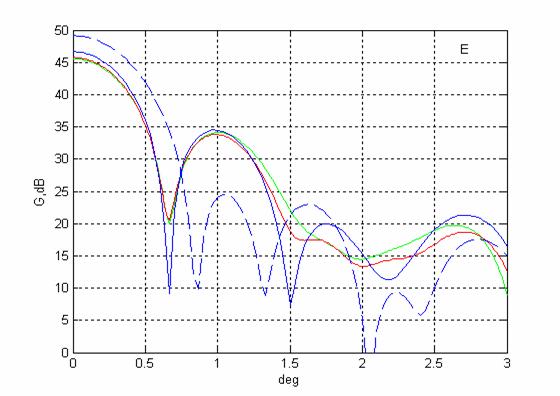
Диаграммы направленности двухзеркальной апланатической

антенны типа Грегори в Е плоскости.

Рис. 5

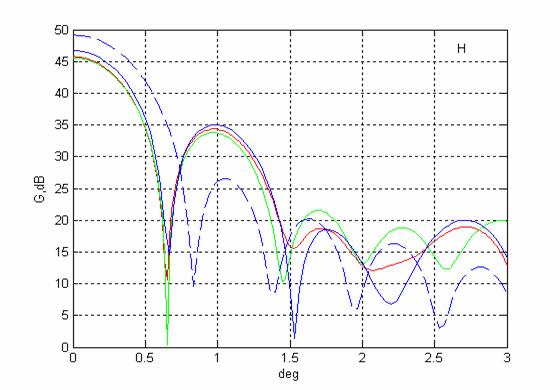
Диаграммы направленности двухзеркальной апланатической

антенны типа Грегори в Н плоскости.

        

         Из рисунков видно, что:

1. Первые два лепестка диаграмм направленности, рассчитанных строгим и приближенным методом, достаточно хорошо совпадают в обеих плоскостях.

2. Абсолютные значения диаграмм направленности, рассчитанных двумя методами, отличаются примерно на 0,9 дБ.

3. Учет затенения вспомогательным зеркалом приводит к падению усиления примерно на 2,5 дБ  и росту относительной величины первого бокового лепестка примерно на 10 дБ.

Отличие абсолютных величин коэффициентов усиления, рассчитанных двумя методами, объясняются, во-первых, отличием коэффициентов усиления моделей облучателей (примерно 0,25 дБ)  и, во-вторых, отличием их фазовых диаграмм направленности. Действительно,  дополнительные расчеты, результаты которых здесь не приводятся, показали, что, изменяя положение гофрированного рупора так, чтобы его фазовый центр совпал с фокальной точкой, можно добиться увеличения коэффициента усиления на 0.4 дБ.

Из вышесказанного следует, что приближенная методика достаточно хорошо моделирует реальную антенну (из рассмотрения исключаются только элементы крепления) и в дальнейшем анализе мы будем использовать только ее.  

 

4.Анализ характеристик сканирования.

 

         Проведем анализ зависимости КИП антенны от угла отклонения луча в зависимости от расстояния облучателя до вспомогательного зеркала при фиксированной ширине диаграммы направленности облучателя и углового размера вспомогательного зеркала. Диаметр апертуры главного зеркала здесь и далее предполагается неизменным. На рисунке 6 показана геометрия антенны типа Кассегрена для трех положений облучателя и соответствующих диаметров апертуры вспомогательного зеркала (0.6, 0.8 и 1 м.). На рисунке 7 соответствующим цветом показаны зависимости КИП от угла отклонения луча. На рисунках 8,9 приведены результаты аналогичных расчетов для антенны типа Грегори. На рисунках 10 - 13 показаны результаты аналогичных расчетов в зависимости от ширины диаграммы направленности облучателя и соответствующего изменения размера вспомогательного зеркала. Из рисунков видно, что, независимо от причины увеличения размера вспомогательного зеркала, характер поведения КИП одинаковый. Т.е. с увеличением апертуры вспомогательного зеркала  для центрального положения луча КИП падает (из-за увеличения затенения), а при увеличении угла отклонения луча кривые зависимости КИПа, соответствующие разным размерам вспомогательного зеркала, сближаются, что объясняется, видимо, уменьшением аберраций при увеличении апертуры вспомогательного зеркала.

         Сравнение аналогичных зависимостей для систем типа Грегори и Кассегрена показывает, что сканирующие свойства первых при прочих равных условиях хуже вторых. Это наглядно видно на рисунках 14, 15.   

 

                       

Рис.6

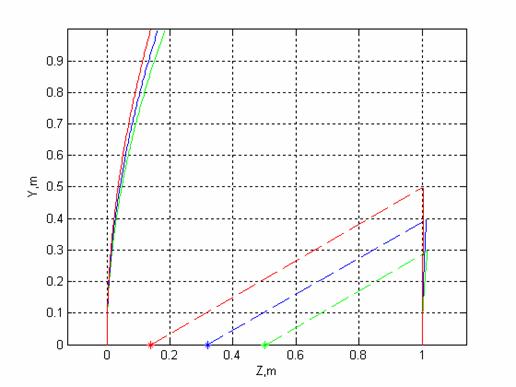
Вид образующих зеркал в системе Кассегрена в зависимости от положения облучателя

 

Рис.7

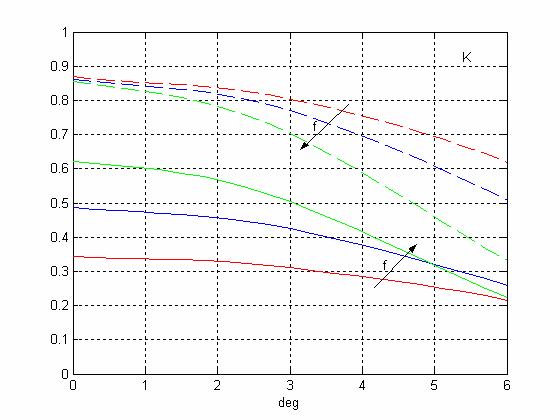
Зависимости КИП системы Касегрена от угла отклонения луча при различных положениях облучателя (пунктирные кривые  - без учета затенения, сплошные кривые - с учетом затенения, d=1м, f=0.14м; 0,32м; 0,5м)

 

 

Рис.8

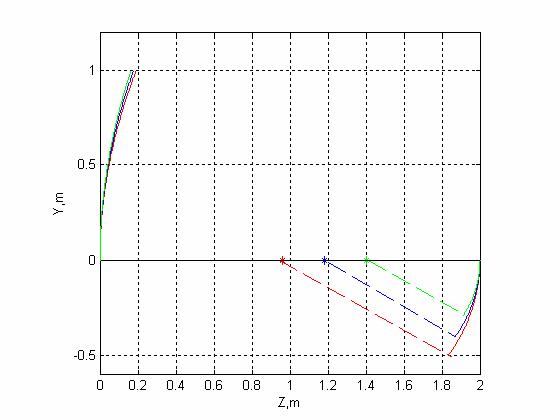
Вид образующих зеркал в системе Грегори в зависимости от положения облучателя

Рис.9.

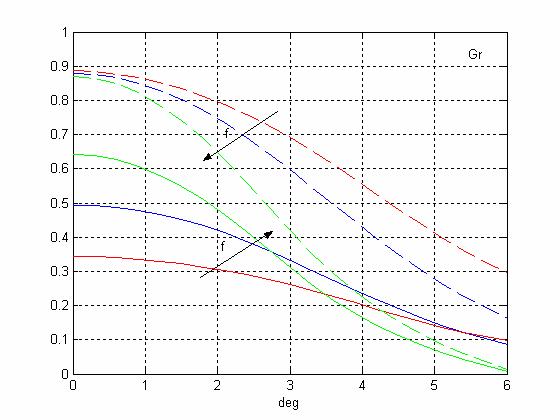
Зависимости КИП системы Грегори от угла сканирования при различных положениях облучателя (пунктирные кривые  - без учета затенения, сплошные кривые - с учетом затенения, d=2м, f=0.96м; 1,18м; 1,4м)

 

Рис10.

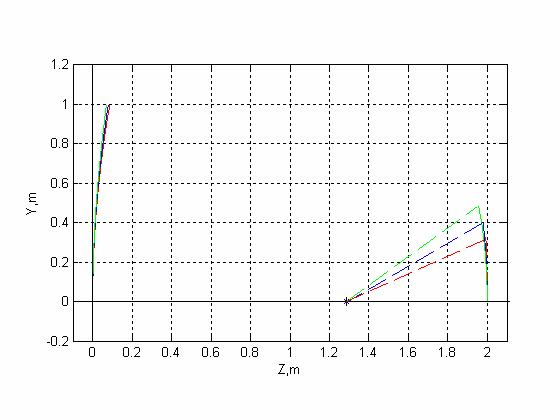
Вид образующих зеркал в системе Касегрена в зависимости от ширины диаграммы направленности облучателя

 

Рис.11

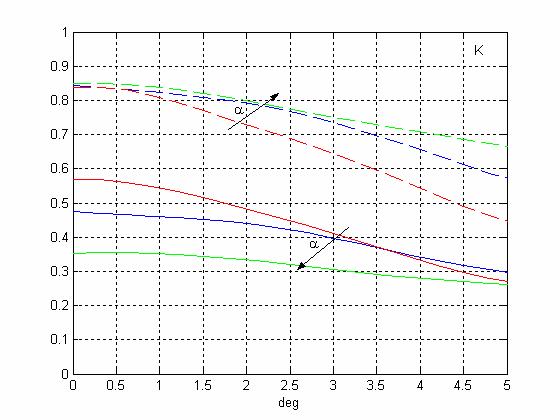
Зависимости КИП системы  Касегрена от угла сканирования при изменении ширины диаграммы направленности облучателя и, соответственно, углового раскрыва вспомогательного зеркала (d=2м, f=1,32м; a_о=50°; 60°; 72°)

 (пунктирные кривые  - без учета затенения, сплошные кривые - с учетом затенения)

 

Рис.12

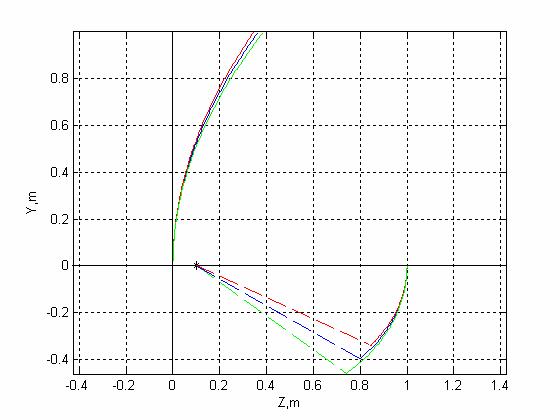
Вид образующих зеркал в системе Грегори в зависимости от ширины диаграммы направленности облучателя и, соответственно, углового раскрыва вспомогательного зеркала

Рис.13

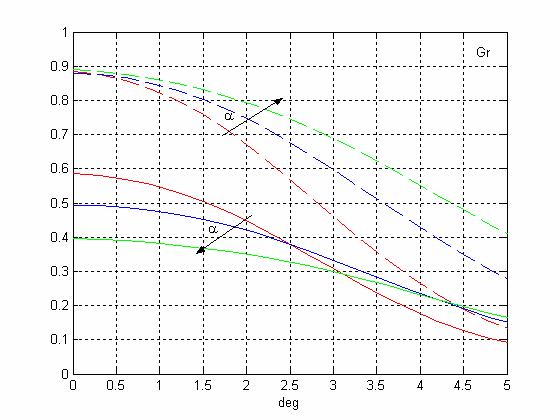
Зависимости КИП системы  Грегори от угла сканирования при изменении ширины диаграммы направленности облучателя  (d=1м, f=0,1м; 2a_о=50°; 60°; 72°)

(пунктирные кривые  - без учета затенения, сплошные кривые - с учетом затенения)

 

Рис.14

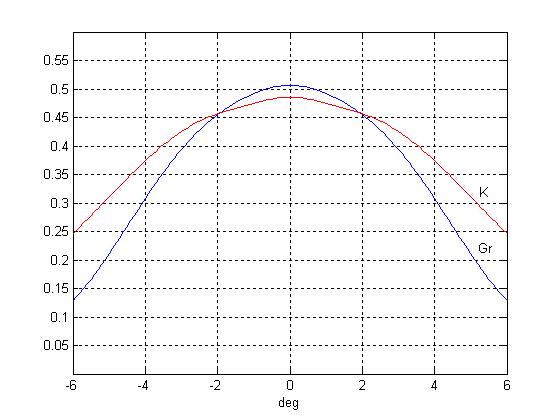
Зависимости КИП систем Кассегрена  (красная кривая) и Грегори (синяя кривая) от угла отклонения луча  (расстояние между зеркалами d=1м)

 

Рис.15

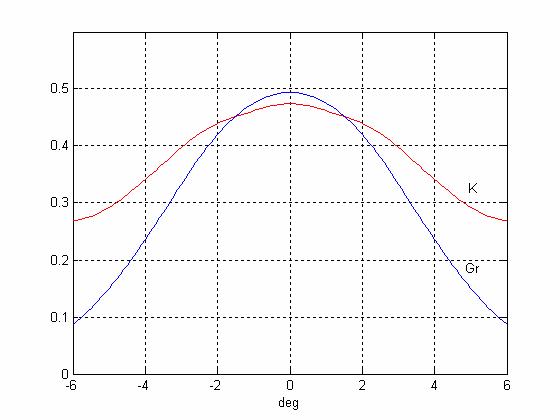
Зависимости КИП систем Касегрена  (красная кривая) и Грегори (синяя кривая) от угла  отклонения луча (d=2м)

 

Рис.16

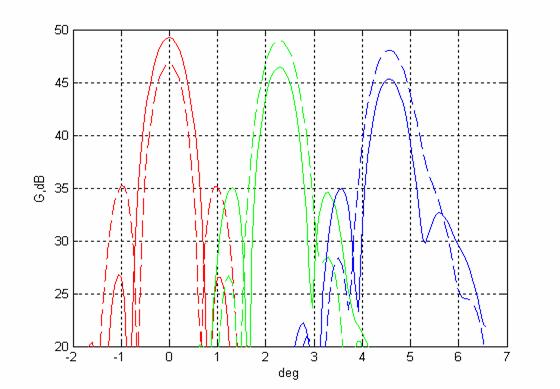
Диаграммы направленности прямого и отклоненных лучей

в системе Кассегрена (d=1; f=0.32)

 

 

Рис.17

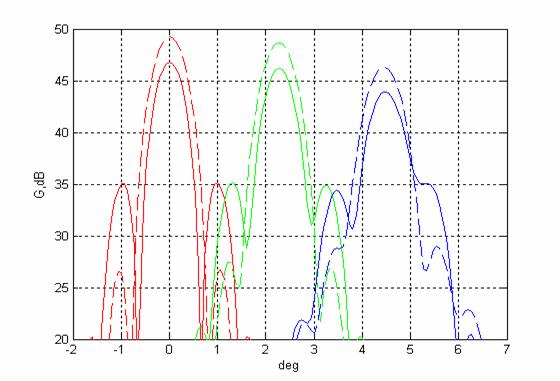
Диаграммы направленности прямого и отклоненных лучей

в системе Грегори (d=1; f=0.1).

 

На рисунках 15, 16 изображены, соответственно,  характеристики сканирования систем Кассегрена и Грегори в виде диаграмм направленности прямого и отклоненного луча. Красные кривые - прямой луч, зеленые и синии – отклоненные лучи,  соответствующие  смещению облучателя вдоль оси X,  соответственно, на 8l и 16l, (пунктир – без учета затенения, сплошные линии – с учетом затенения). Из анализа кривых следует, что с увеличением угла отклонения  вместе с падением максимума усиления происходит искажение луча, появляется асимметрия  боковых лепестков, причем абсолютный уровень первого бокового лепестка в системах Грегори и Кассегрена примерно одинаковый.

  

Литература.

 

1. Schwarzchild K. Untersuchungen zur geometrischen Optik. Pt. II. Wiss Cottingen Math. Phys., 1905, Klasse IV.

2. Бахрах Л.Д., Галимов Г.К.  Зеркальные сканирующие антенны. М.: Наука,1981.