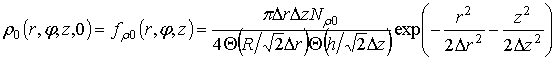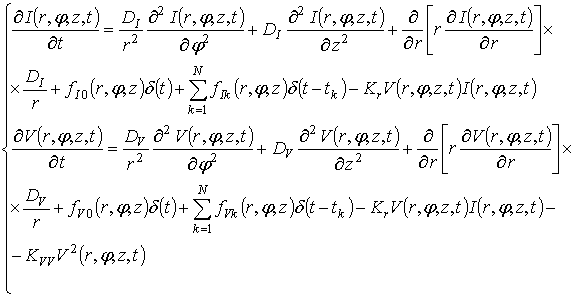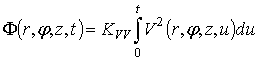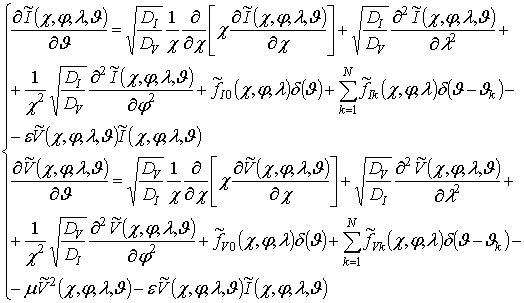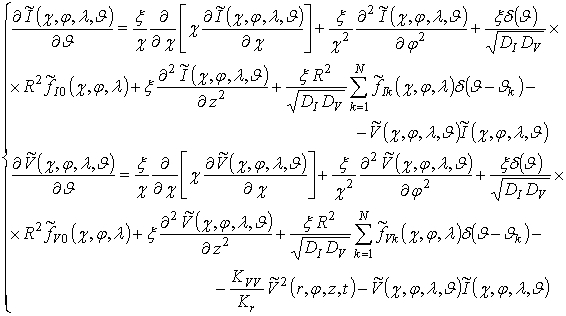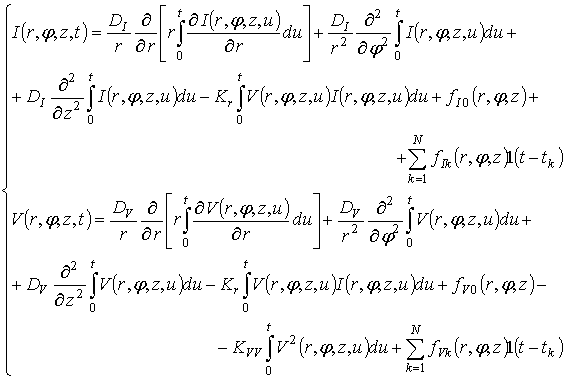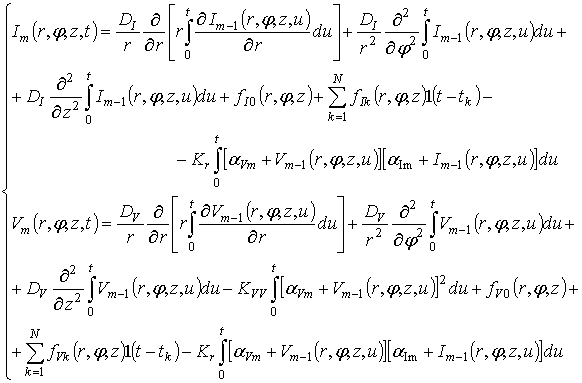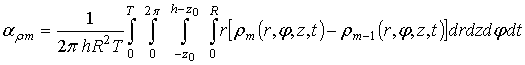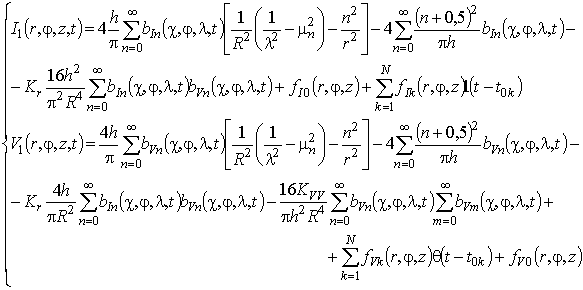РАСЧЕТ ЭВОЛЮЦИИ КЛАСТЕРОВ РАДИАЦИОННЫХ ДЕФЕКТОВ С УЧЕТОМ ДИФФУЗИИ И НЕКОТОРЫХ ВТОРИЧНЫХ ПРОЦЕССОВ
Е.Л. Панкратов
Институт физики
микроструктур РАН,
Нижний Новгород
Получена 26 мая 2007 г.
В настоящей работе проведен анализ эволюции концентрации точечных дефектов при ионном облучении твердых тел. Предложена приближенная аналитическая методика для ее описания с учетом диффузии и некоторых вторичных процессов (рекомбинация точечных дефектов и образование дивакансий). Расчеты произведены с учетом дискретного во времени и пространстве попадания ионов на поверхность образца. На примере облучения кремния ионами неона рассчитаны зависимости концентрации дефектов от глубины при различных дозах (временах облучения) и зависимость дозы аморфизации от плотности ионного тока.
Введение
Вопрос об образовании и эволюции концентрации точечных дефектов при ионном облучении является одним из ключевых в физике ионной имплантации и радиационной физике. Несмотря на то, что этому вопросу уделялось много внимания, в том числе в теоретических работах, существующие аналитические подходы в основном ограничиваются либо слишком грубыми, либо асимптотическими приближениями [1,2]. При этом обычно не учитываются реальные факторы, такие как плотность потока частиц (плотности тока в случае ионного облучения). Учет этих факторов приводит к математическим трудностям при получении аналитических решений, численные же методы обладают известными недостатками.
В настоящей работе сделана попытка развития приближенного аналитического подхода к этой проблеме с учетом представляющихся наиболее важными вторичных процессов [3,4].
В настоящей работе рассмотрена среда, в которой образовался кластер точечных радиационных дефектов (вакансий и междоузельных атомов) с эллипсоидальной симметрией и гауссовым распределением концентрации после попадания в нее быстрой частицы (например, иона). Дефекты диффундируют с постоянным коэффициентом диффузии и участвуют в образовании дивакансий (по бимолекулярному механизму). Одновременно происходит прямая рекомбинация дефектов друг с другом. В работе определялись концентрации междоузельных атомов, вакансий и дивакансий, как функции координат и времени, при наложении (в пространстве и времени) на кластер дефектов, сформированный одной радиационной частицей (ионом), кластеров, созданных другими частицами (ионами), в зависимости от дозы и плотности ионного тока. Такая модель позволяет моделировать процесс дефектообразования при различных скоростях набора дозы, в частности, прогнозировать дозы аморфизации. Этот анализ полезен при формировании наноструктур методом ионного облучения кремния [5,6] в зависимости от сорта ионов и плотности ионного тока. Данная задача решена методом осреднения функциональных поправок с улучшенной сходимостью. Особенностью данного подхода по сравнению с более распространенным, когда концентрация дефектов считается непрерывной и однородной по поверхности образца, является учет пространственно-временной дискретности падения ионов на образец. Следует также заметить, что в аналогичных работах (см., например, [1]) по моделированию стабилизации кластеров дефектов рассматривались предельные случаи медленной и быстрой диффузии (из рассмотрения динамики перераспределения дефектов исключались соответственно или диффузионная составляющая, или все остальные). Данная работа является обобщением этих предельных случаев.
Методика анализа
Рассмотрим
эволюцию концентрации радиационных дефектов, образовавшихся в результате
попадания в образец твердого тела радиационных частиц (ионов). В этом случае
область распространения дефектов близка по форме к цилиндрической. В результате
попадания одной частицы образуется кластер дефектов. Предполагается, что
междоузельные атомы имеют существенно больший коэффициент диффузии и покидают
поврежденную область образца быстрее вакансий. Распределение концентрации междоузельных
атомов ![]() и вакансий
и вакансий ![]() по радиальной
по радиальной ![]() , угловой
, угловой ![]() и осевой
и осевой ![]() координатам в момент окончания динамической стадии эволюции каскада,
принятый за начало отсчета по времени
координатам в момент окончания динамической стадии эволюции каскада,
принятый за начало отсчета по времени ![]() , имеет вид:
, имеет вид:
где 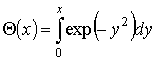 - функция ошибок [7];
- функция ошибок [7]; ![]() ;
; ![]() и
и ![]() – полное количество междоузельных
атомов и вакансий в начальный момент времени;
– полное количество междоузельных
атомов и вакансий в начальный момент времени; ![]() и
и ![]() – область распространения дефектов;
– область распространения дефектов; ![]() – координата облучаемой поверхности
образца. Здесь
– координата облучаемой поверхности
образца. Здесь ![]() – толщина образца, которая считается
большой по сравнению с пробегом ионов, а
– толщина образца, которая считается
большой по сравнению с пробегом ионов, а ![]() вводится таким образом, чтобы эта величина была большой по
сравнению с поперечным радиусом кластера и поэтому выбор
вводится таким образом, чтобы эта величина была большой по
сравнению с поперечным радиусом кластера и поэтому выбор ![]() слабо влияет на результат. Плоскость
слабо влияет на результат. Плоскость
![]() совпадает с
плоскостью, на которой расположен максимум начального распределения дефектов по
оси
совпадает с
плоскостью, на которой расположен максимум начального распределения дефектов по
оси ![]() ; угловая
координата изменяется в интервале
; угловая
координата изменяется в интервале ![]() . С течением времени часть точечных дефектов
продиффундирует за пределы исходного кластера, другая часть - образует
комплексы (в данной работе ограничимся образованием дивакансий), третья часть –
рекомбинирует при взаимодействии друг с другом. Во время эволюции данного
кластера в образец в случайные моменты времени
. С течением времени часть точечных дефектов
продиффундирует за пределы исходного кластера, другая часть - образует
комплексы (в данной работе ограничимся образованием дивакансий), третья часть –
рекомбинирует при взаимодействии друг с другом. Во время эволюции данного
кластера в образец в случайные моменты времени ![]() попадают другие частицы (будем
считать, что попало N
новых частиц с одинаковой энергией и одинаковым пробегом
попадают другие частицы (будем
считать, что попало N
новых частиц с одинаковой энергией и одинаковым пробегом ![]() ), образуя при этом новые
кластеры с количеством дефектов в каждом
), образуя при этом новые
кластеры с количеством дефектов в каждом ![]() и
и ![]() и координатами максимума
и координатами максимума ![]() ,
, ![]() и
и ![]() . Их начальное распределение:
. Их начальное распределение:
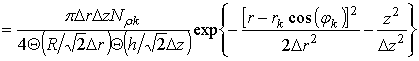 , (1a)
, (1a)
где ![]() .
.
Динамика
точечных радиационных дефектов на этапе стабилизации кластеров может быть
описана с учетом их диффузии, а также их рекомбинации друг с другом и
образования дивакансий. В цилиндрической системе координат ![]() можно записать:
можно записать:
где ![]() и
и ![]() – концентрации междоузельных атомов и вакансий образованных всеми
каскадами;
– концентрации междоузельных атомов и вакансий образованных всеми
каскадами; ![]() ,
, ![]() ,
, ![]() и
и ![]() – соответственно коэффициенты
диффузии междоузельных атомов и вакансий, кинетические коэффициенты захвата
вакансии вакансией (при образовании дивакансий) и рекомбинации [8],
– соответственно коэффициенты
диффузии междоузельных атомов и вакансий, кинетические коэффициенты захвата
вакансии вакансией (при образовании дивакансий) и рекомбинации [8], ![]() ) – односторонняя дельта-функция Дирака [7].
Содержащие дельта-функцию слагаемые системы уравнений (2) соответствуют
генерации новых кластеров дефектов при попадании в образец новых ионов. Данная
система должна быть дополнена описывающим перераспределение дивакансий
уравнением, которое может быть записано в следующем виде:
) – односторонняя дельта-функция Дирака [7].
Содержащие дельта-функцию слагаемые системы уравнений (2) соответствуют
генерации новых кластеров дефектов при попадании в образец новых ионов. Данная
система должна быть дополнена описывающим перераспределение дивакансий
уравнением, которое может быть записано в следующем виде:
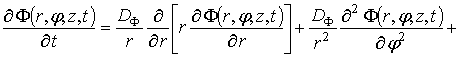
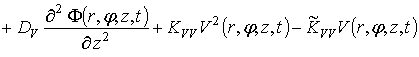 ,
,
где ![]() и
и ![]() – соответственно концентрация и коэффициент диффузии дивакансий,
– соответственно концентрация и коэффициент диффузии дивакансий, ![]() - кинетический коэффициент распада дивакансий. Однако,
параметры
- кинетический коэффициент распада дивакансий. Однако,
параметры ![]() и
и ![]() обычно существенно меньше соответственно
обычно существенно меньше соответственно ![]() и
и ![]() , а также KVV. По этой причине концентрация дивакансий может быть определена с помощью
следующего соотношения [1]:
, а также KVV. По этой причине концентрация дивакансий может быть определена с помощью
следующего соотношения [1]:
Систему
уравнений (2) необходимо дополнить граничными условиями. Формально радиальная
составляющая ее общего решения является суперпозицией функций Бесселя первого
порядка первого и второго рода соответственно. Однако, функции Бесселя второго
рода являются физически нереализуемыми, что приводит к необходимости
приравнивания нулю соответствующей постоянной интегрирования. Ввиду того, что
дефекты фактически не достигают границ ![]() и
и ![]() (значение
(значение ![]() выбиралось так, чтобы процессы, происходящие при
выбиралось так, чтобы процессы, происходящие при ![]() , не оказывали заметного
влияния), концентрация дефектов непрерывна, отсутствуют отрицательные значения
угловых координат, и считается равным нулю поток дефектов в область значений
осевой координаты
, не оказывали заметного
влияния), концентрация дефектов непрерывна, отсутствуют отрицательные значения
угловых координат, и считается равным нулю поток дефектов в область значений
осевой координаты ![]() (отражающая поверхность), можно использовать следующие граничные условия:
(отражающая поверхность), можно использовать следующие граничные условия:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 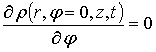 ,
, 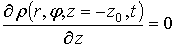 .
.
В общем
случае на перераспределение междоузельных атомов и вакансий, описываемое
системами уравнений (2) или (4), оказывают влияние диффузия точечных дефектов,
комплексообразование (образование дивакансий) и взаимодействие вакансий с
междоузельными атомами. Для оценки относительного влияния тех или иных
процессов на накопление дефектов и дозу аморфизации рассчитаем так называемые
функции влияния [9]. Обычно для качественных и некоторых количественных оценок
достаточно расчета линейных функций влияния. В нашем случае соответствующие
функции имеют вид: 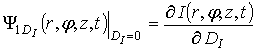 ,
,
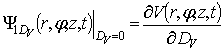 ,
, 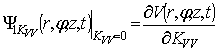 ,
, ![]()
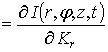 и
и 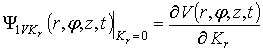 . Иногда требуется учет квадратичных
функций влияния, соответственно равных
. Иногда требуется учет квадратичных
функций влияния, соответственно равных ![]()
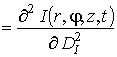 ,
, 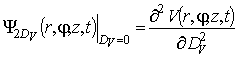 ,
, 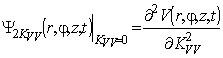 ,
, 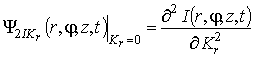 и
и 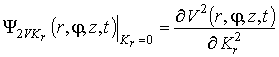 . Функции влияния могут быть вычислены следующим
образом. Запишем исходное уравнение (2) в безразмерных переменных:
. Функции влияния могут быть вычислены следующим
образом. Запишем исходное уравнение (2) в безразмерных переменных:
где 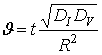 ,
, 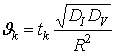 ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, 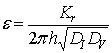 ,
, 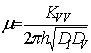 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для
определения функций влияния запишем решение системы уравнений (2а) в виде
степенных рядов: 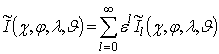 и
и
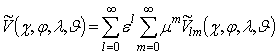 . Можно показать
(см., например, [10]), что функция
. Можно показать
(см., например, [10]), что функция ![]() совпадает с линейной функцией влияния образования
дивакансий, а функции
совпадает с линейной функцией влияния образования
дивакансий, а функции ![]() и
и
![]() совпадают с
линейными функциями влияния рекомбинации на перераспределение радиационных
дефектов. Функции
совпадают с
линейными функциями влияния рекомбинации на перераспределение радиационных
дефектов. Функции ![]() ,
,
![]() и
и ![]() совпадают с
аналогичными квадратичными функциями влияния. Для определения функций влияния
диффузионного “расплывания” точечных радиационных дефектов целесообразно ввести
другие безразмерные величины:
совпадают с
аналогичными квадратичными функциями влияния. Для определения функций влияния
диффузионного “расплывания” точечных радиационных дефектов целесообразно ввести
другие безразмерные величины: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 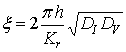 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В этом случае уравнения (2) преобразуются к следующему
виду:
. В этом случае уравнения (2) преобразуются к следующему
виду:
Решение
данного уравнения может быть получено по аналогии с решением уравнения (2а),
т.е. в виде ряда: 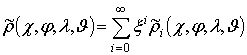 .
Функции
.
Функции ![]() и
и ![]() совпадают
соответственно с линейной и квадратичной функциями влияния диффузии точечных
дефектов на эволюцию их распределения (см., например, [10]). Анализ функций влияния
показал, что для параметров, принятых в наших расчетах, преобладающий вклад в
эволюцию распределения дефектов дает их диффузионное “расплывание”.
Рекомбинация дефектов является следующим по значимости эффектом. Процесс
образования дивакансий оказывает минимальное влияние на распределение дефектов.
совпадают
соответственно с линейной и квадратичной функциями влияния диффузии точечных
дефектов на эволюцию их распределения (см., например, [10]). Анализ функций влияния
показал, что для параметров, принятых в наших расчетах, преобладающий вклад в
эволюцию распределения дефектов дает их диффузионное “расплывание”.
Рекомбинация дефектов является следующим по значимости эффектом. Процесс
образования дивакансий оказывает минимальное влияние на распределение дефектов.
Представляет интерес также влияние диффузии дефектов и их комплексообразования на дозу аморфизации. Расчет соответствующих функций влияния показывает, что и ускорение диффузии, и замедление комплексообразования дефектов приводят к увеличению дозы, необходимой для достижения аморфизации.
Преобразуем систему уравнений (2) к следующей системе интегро-дифференциальных уравнений:
где ![]() – переменная
интегрирования по времени, временная единичная функция определяется следующим
соотношением [7]:
– переменная
интегрирования по времени, временная единичная функция определяется следующим
соотношением [7]: ![]() .
.
Решение
системы уравнений (4) производится приближенно с помощью метода осреднения
функциональных поправок (см., например, [11,12]). В рамках данного метода
функции ![]() и
и ![]() , а также их производные в правой части системы уравнений (4)
в первом приближении заменяются на пока не известные постоянные:
, а также их производные в правой части системы уравнений (4)
в первом приближении заменяются на пока не известные постоянные: ![]() и
и ![]() и т.д. Далее полученное решение уточняется следующим образом.
Концентрация вакансий в m-ом
приближении определяется из системы уравнений (4) через концентрации дефектов в
(m-1)-ом приближении путем замены в
правых частях уравнений:
и т.д. Далее полученное решение уточняется следующим образом.
Концентрация вакансий в m-ом
приближении определяется из системы уравнений (4) через концентрации дефектов в
(m-1)-ом приближении путем замены в
правых частях уравнений: ![]() ,
, ![]() , т.е.
, т.е.
где
t=T – момент окончания наблюдения за эволюцией концентрации дефектов (после попадания N ионов).
Подстановка
(5) в (6) позволяет получить соотношения для функций ![]() и
и ![]() , а также параметров
, а также параметров ![]() и
и ![]() в окончательном виде. Они не
приводятся из-за громоздкости. Практическое применение данного метода
затруднено медленной сходимостью. Для ускорения сходимости функции
в окончательном виде. Они не
приводятся из-за громоздкости. Практическое применение данного метода
затруднено медленной сходимостью. Для ускорения сходимости функции ![]() и
и ![]() в правой части (4) в первом приближении заменим не на постоянную
величину, а на более точную аппроксимацию, например, на решение уравнения (2) в
чисто диффузионном приближении. В результате такой замены из (4) получаем
первое приближение для концентрации радиационных дефектов в модифицированном
методе осреднения:
в правой части (4) в первом приближении заменим не на постоянную
величину, а на более точную аппроксимацию, например, на решение уравнения (2) в
чисто диффузионном приближении. В результате такой замены из (4) получаем
первое приближение для концентрации радиационных дефектов в модифицированном
методе осреднения:
где 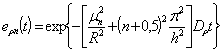 ,
, 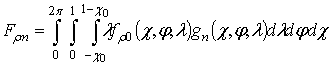 ,
, 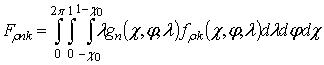 ,
, ![]() ,
, ![]() ,
, ![]() . Здесь
. Здесь ![]() - функция Бесселя первого рода первого порядка,
- функция Бесселя первого рода первого порядка, ![]() – корень уравнения
– корень уравнения ![]() ,
, 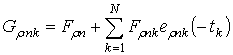 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Подстановка пространственно-временного распределения вакансий в соотношение (3) позволяет найти пространственно-временное распределение концентрации дивакансий. В данной работе получено первое приближение пространственно-временного распределения дивакансий. Приближения более высоких порядков пространственно-временного распределения концентрации вакансий вычисляются аналогично, используя (5)-(6), а затем из (3) определяются соответствующие приближения пространственно-временного распределения дивакансий.
Результаты анализа
Расчет
проводился для случая облучения кремния ионами Ne+ с энергией 100 кэВ. Параметры распределения дефектов
в каскаде, согласно [13], следующие: ![]() нм;
нм; ![]() нм;
нм; ![]() нм. Для параметров
нм. Для параметров ![]() ,
, ![]() ,
, ![]() и
и ![]() приняты значения [3,4,8]:
приняты значения [3,4,8]: ![]() см2/с,
см2/с, ![]() см2/с,
см2/с, ![]() см-3с-1 и
см-3с-1 и ![]() см-3с-1. В общем случае данный метод
требует выбора радиуса R
и числа N падающих на площадку частиц. Так как
число
см-3с-1. В общем случае данный метод
требует выбора радиуса R
и числа N падающих на площадку частиц. Так как
число ![]() при
определенном
при
определенном ![]() и дозе фиксировано, то фактически
выбирается только параметр
и дозе фиксировано, то фактически
выбирается только параметр ![]() . Очевидно, что чем большее значение
. Очевидно, что чем большее значение ![]() , тем лучше статистика и точнее будет результат, но более длителен
расчет. Для определения минимально приемлемых значений
, тем лучше статистика и точнее будет результат, но более длителен
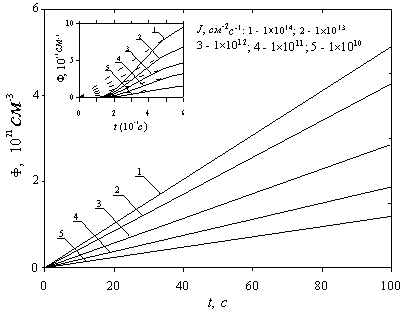
расчет. Для определения минимально приемлемых значений ![]() были выполнены расчеты
были выполнены расчеты ![]() ,
, ![]() и
и ![]() при различных значениях
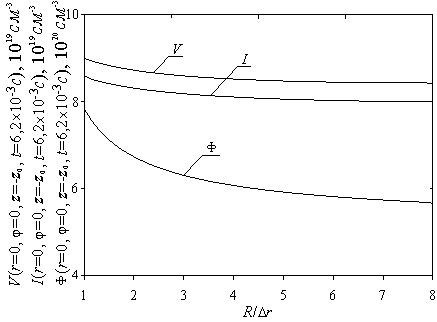
при различных значениях ![]() . Результаты расчета приведены на рис. 1, из которого
видно, что
. Результаты расчета приведены на рис. 1, из которого
видно, что ![]() ,
, ![]() и
и ![]() при
при ![]() становятся слабо зависящими от величины
становятся слабо зависящими от величины ![]() . При этом имеет место достаточно хорошее сглаживание
флуктуаций, связанных со статистическим разбросом распределения дефектов от
разных каскадов.
. При этом имеет место достаточно хорошее сглаживание
флуктуаций, связанных со статистическим разбросом распределения дефектов от
разных каскадов.
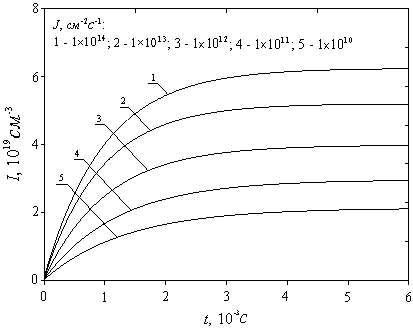
На рис.
2а
и 2б приведены временные зависимости концентрации междоузельных атомов и
вакансий в начале координат (при R=4Dr) при различных плотностях потока
частиц J (плотность тока варьировалась от 1,6´10-3 до 16 мкА/см2).
Видно, что при заданных параметрах ![]() и
и ![]() выходят на квазистационарный уровень
примерно за ~5´10-4с
и ~6´10-4с практически
независимо от плотности ионного тока. С ростом J этот уровень, естественно, увеличивается. Скачки
концентраций точечных дефектов, связанные с дискретностью падения ионов, в
выбранном масштабе не заметны.
выходят на квазистационарный уровень
примерно за ~5´10-4с
и ~6´10-4с практически
независимо от плотности ионного тока. С ростом J этот уровень, естественно, увеличивается. Скачки
концентраций точечных дефектов, связанные с дискретностью падения ионов, в
выбранном масштабе не заметны.
Рис.1. Зависимость расчетных значений
концентрации вакансий и междоузельных атомов (в единицах 1019 см-3),
а также дивакансий (в единицах 1020 см-3) в точке (![]() ,
,![]() ,
,![]() ) при
) при ![]() с от выбора радиуса R облучаемой площадки. Выбор
с от выбора радиуса R облучаемой площадки. Выбор ![]() с соответствует
времени падения 17-ой частицы при
с соответствует
времени падения 17-ой частицы при ![]() см-2с-1 (доза
см-2с-1 (доза ![]() см-2)
см-2)
Рис.2а. Зависимость
концентрации междоузельных атомов I(r=0,j =0,z=0) от времени при R=4Dr для различных значений J
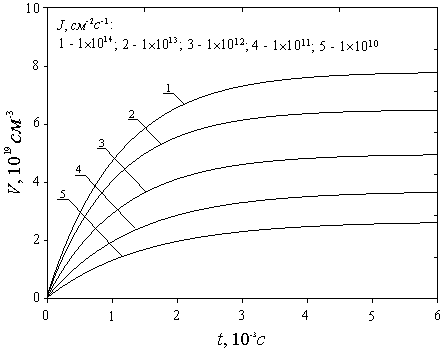
Рис.2б. Зависимость
концентрации вакансий V(r=0,j =0,z=0) от времени при R=4Dr для различных значений J
На рис. 3 представлена временная зависимость концентрации дивакансий в начале координат при тех же значениях J, что и на рис. 2. Видно, что F(r,j,z,t) растет со временем (т.е. с дозой) сначала с возрастающей скоростью (вследствие роста концентрации вакансий, из которых дивакансии образуются по бимолекулярному механизму), а затем – практически линейно (в области времен, при которых V(r,j,z,t) выходит на квазистационарное значение).
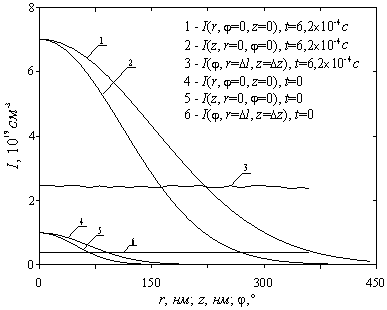
На рис. 4а,
4б и 5 приведены распределения междоузельных атомов, вакансий и дивакансий
к моменту попадания частицы с k=17,
что соответствует дозе F»1,2´1011 см-2.
Плотность потока взята равной J=2´1013 см-2с-1
(3 мкА/см2). Получено, что при дальнейшем увеличении числа ионов профиль
меняется слабо. Как видно из рис. 4, для принятых нами параметров за времена,
сравнимые со временем выхода V
на уровень насыщения, происходит расплывание кластера вакансий. Размер кластера
дивакансий (рис. 5) меньше размера кластера вакансий. Последнее связано с
бимолекулярным механизмом образования дивакансий. Угловые распределения I, V и F, как и следовало ожидать, практически однородны вследствие симметрии
задачи.
Рис.3.
Зависимость концентрации
дивакансий ![]() от
времени при
от
времени при ![]() для
различных значений J
для
различных значений J
Рис. 4а. Зависимость концентрации междоузельных
атомов осевой (z), радиальной (r) и угловой
координат (![]() )
после попадания 17-ой частицы (доза
)
после попадания 17-ой частицы (доза ![]() см-2) на площадку с радиусом
см-2) на площадку с радиусом ![]() при
при ![]() см-2с-1
(кривые 1-3) и распределения междоузельных атомов от одной частицы (кривые
4-6). Для кривых 4-6 значение концентрации I увеличено
в 10 раз
см-2с-1
(кривые 1-3) и распределения междоузельных атомов от одной частицы (кривые
4-6). Для кривых 4-6 значение концентрации I увеличено
в 10 раз
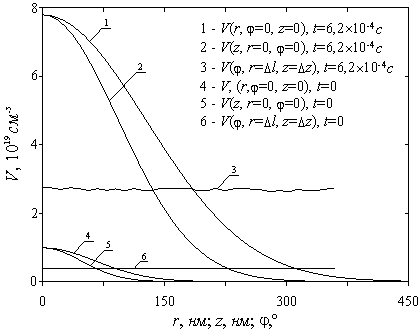
Рис.4б. Зависимость концентрации вакансий
осевой (z), радиальной (r) и угловой
координат (![]() )
после попадания 17-ой частицы (доза
)
после попадания 17-ой частицы (доза ![]() см-2) на площадку с радиусом
см-2) на площадку с радиусом ![]() при
при ![]() см-2с-1
(кривые 1-3) и распределения вакансий от одной частицы (кривые 4-6). Для кривых
4-6 значение концентрации V увеличено в 10 раз
см-2с-1
(кривые 1-3) и распределения вакансий от одной частицы (кривые 4-6). Для кривых
4-6 значение концентрации V увеличено в 10 раз
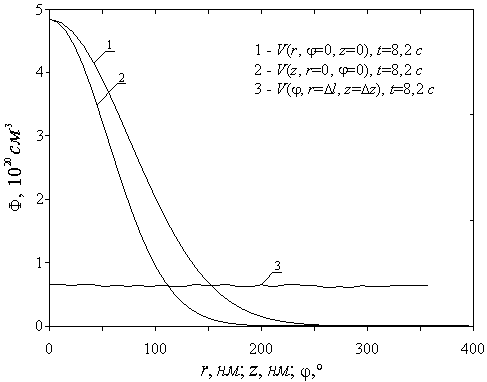
Рис.5. Зависимость концентрации
дивакансий от радиальной, осевой и угловой координат при дозе ![]() см-2,
см-2,![]() см-2с-1 (3 мкА/см2)
см-2с-1 (3 мкА/см2)
Были
получены дозы аморфизации как функции J. За дозу аморфизации принималась доза, при которой
концентрация дивакансий достигала 10% от числа атомов кремния Si в 1 см3. Из рис. 6 видно,
что при малых J дозах
аморфизации ![]() ,
при больших значениях J
она падает приблизительно по закону
,
при больших значениях J
она падает приблизительно по закону ![]() , затем снова стремится к постоянному значению. При малых значениях J зависимость Fам от плотности тока при постоянной
дозе слабая из-за того, что свободные вакансии в кластере от каждой частицы
почти успевают исчезнуть к моменту попадания в его область следующих частиц,
так что кластеры от отдельных частиц эволюционируют квазинезависимо друг от
друга. При очень больших J
практически все вакансии, генерированные каждой падающей частицей, к моменту
удара следующей частицы выживают в свободном виде, поэтому концентрация
дивакансий определяется только дозой, и зависимость от J должна исчезать. Полученные нами
дозы аморфизации при плотности тока 1¸10 мкА/ см2 по порядку
величины согласуются с экспериментальными значениями [16], что свидетельствует
об адекватном выборе параметров задачи.
, затем снова стремится к постоянному значению. При малых значениях J зависимость Fам от плотности тока при постоянной
дозе слабая из-за того, что свободные вакансии в кластере от каждой частицы
почти успевают исчезнуть к моменту попадания в его область следующих частиц,
так что кластеры от отдельных частиц эволюционируют квазинезависимо друг от
друга. При очень больших J
практически все вакансии, генерированные каждой падающей частицей, к моменту
удара следующей частицы выживают в свободном виде, поэтому концентрация
дивакансий определяется только дозой, и зависимость от J должна исчезать. Полученные нами
дозы аморфизации при плотности тока 1¸10 мкА/ см2 по порядку
величины согласуются с экспериментальными значениями [16], что свидетельствует
об адекватном выборе параметров задачи.
Сравнение
полученных аналитических результатов для первого приближения с результатами
прямого численного решения системы уравнений (2) показывает различие в 5¸7 %. Это свидетельствует о быстрой сходимости
используемого нами метода.
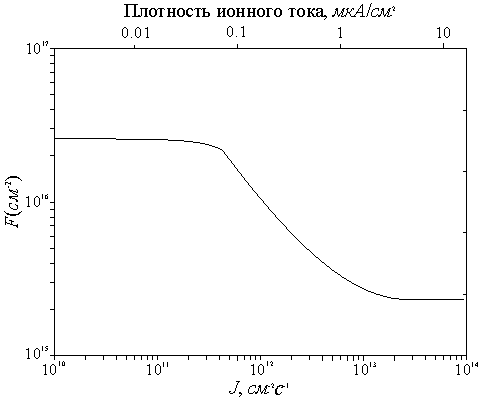
Рис.6. Зависимость дозы аморфизации Fам от плотности потока частиц (за Fам принята доза, при которой V составляет 10% от числа атомов Si в 1 см-3)
Заключение
В настоящей работе проведен анализ эволюции кластеров точечных радиационных дефектов при ионном облучении с учетом диффузии и наиболее важных вторичных эффектов (рекомбинация и образование дивакансий). Получена зависимость дозы аморфизации (на примере Ne+ с энергией 100 кэВ) от плотности ионного тока. Проведен анализ относительного влияния изменений параметров эволюции дефектов на их концентрацию. Данный метод расчета применим не только к ионному, но и к другим видам дефектообразования под действием “надпороговой” радиации.
Литература
[1] В.Л. Винецкий, Г.А. Холодарь. Радиационая физика полупроводников. Киев: "Наукова думка", 1979.
[2] L. Pelaz, L. Marques and J. Barbolla // J. Appl. Phys. 2004. V.96. №11. P. 5947.
[3] N.P. Morozov, D.I. Tetelbaum, P.V. Pavlov, and E.I. Zorin. // Phys. Stat. Sol. 1976. V.37. №1. P.57.
[4] Н.П. Морозов, Д.И. Тетельбаум // ФТП. 1980. Т.14. №5. С. 934.
[5] Д.И. Тетельбаум, С.А. Трушин, А.В. Питиримов // Известия академии инженерных наук им. А.М. Прохорова. Технология материалов и компонентов электронной техники. 2004. Т.7. №11. С. 17.
[6] А.А. Ежевский, Д.И. Тетельбаум, А.Н. Михайлов А.А. Ежевский, Д.И. Тетельбаум, А.Н. Михайлов, М.Ю. Лебедев, Ю.А. Менделеева, С.В. Морозов, Д.В. Гусейнов.// Optical Materials. 2001. V.17. №1-2. P. 57.
[7] Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1974.
[8] P.M. Fahey, P.B. Griffin, J.D. Plummer // Rev. Mod. Phys. 1989. V.61. №2. P. 289.
[10] E.L. Pankratov // Phys. Rev. B. 2005. V.72. №7. P. 075201.
[11] Ю.Д. Соколов // Прикладная механика. 1955. Т.1. С. 23.
[12] А.Ю. Лучка. Теория и применение метода осреднения функциональных поправок. Киев: Издательство АН УССР. 1963.
[13] А.Ф. Буренков, Ф.Ф. Комаров, М.А. Кумахов, М.М. Темкин. Пространственные распределения энергии, выделенной в каскадах атомных столкновений в твердых телах. М.: Энергоатомиздат, 1985. 248 с.
[14] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. М.: Энергия, 1975. 130 с.