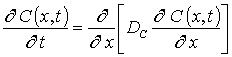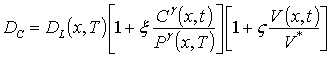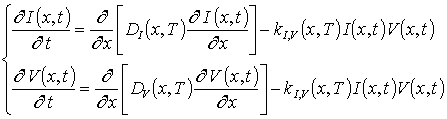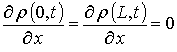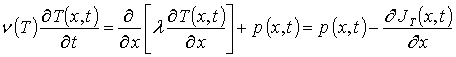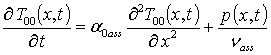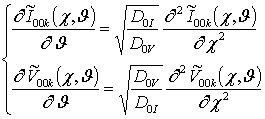Уменьшение глубины залегания p-n-переходов в полупроводниковой гетероструктуре путем последовательных радиационной обработки материалов и микроволнового отжига
Е. Л. Панкратов
Нижегородский архитектурно-строительный университет
Получена 13 июля 2011 г.
Аннотация. Ранее было показано, что формирование диффузионных и имплантационных p-n-переходов в полупроводниковых гетероструктурах после соответствующего выбора ее материалов и оптимизации длительности отжига позволяет сформировать p-n-переходы с более компактным и равномерным в обогащенной области распределением примеси. Формирование неоднородного температурного поля применением лазерного или микроволнового отжигов позволяет усилить оба эффекта. Из эксперимента известно, что предварительная радиационная обработка материалов приводит к изменению перераспределения примеси в процессе отжига. В настоящей работе рассматривается возможность применения последовательных радиационной обработки материалов гетероструктуры и микроволнового отжига для одновременного усиления эффектов увеличения компактности распределения примеси в имплантационном p-n-переходе и увеличения ее равномерности в обогащенной области.
Ключевые слова: увеличение резкости p-n-переходов; биполярные гетеротранзисторы; оптимизация отжига; радиационная обработка материалов; микроволновый отжиг.
Abstract. It has recently been shown, that manufacturing of diffusive-junction rectifiers and implanted-junction rectifiers in a semiconductor heterostructure after appropriate choosing of parameters of the structure and optimization of annealing time leads to increase of the sharpness of p-n-junction and at one time to increase the homogeneity of dopant distribution in doped area. Formation of inhomogeneity of temperature in the heterostructure by laser or microwave annealing gives us possibility to increase the both effects at one time. It has recently been shown by experiments, that predoping radiation processing of materials leads to changing of dopant diffusion in comparison with nonprocessed one. In this paper we consider the possibility to use serial radiation processing of materials of heterostructure before doping and microwave annealing of radiation defects after doping to increase the sharpness p-n-junctions and at one time to increase the homogeneity of dopant distribution in doped area in the heterostructure.
Keywords: increasing of sharpness of p-n-junctions; bipolar heterotransistors; optimization of annealing; radiation processing of materials; microwave annealing.
Введение
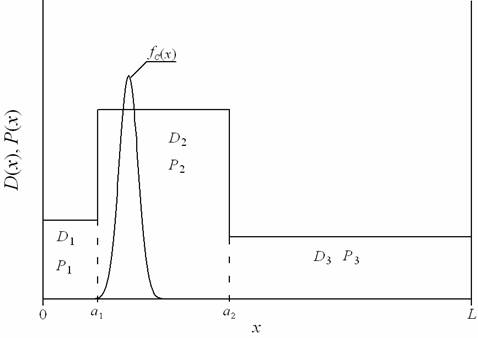
В настоящее время происходит интенсивное увеличение степени интеграции элементов интегральных схем (ИС), а также увеличения их быстродействия и надежности (в случае p-n-переходов и их систем) [1-3]. Одновременно происходит уменьшение глубины залегания элементов ИС. Для увеличения быстродействия осуществляется поиск новых материалов с более высокими скоростями носителей заряда [1-3]. Увеличения быстродействия, степени интеграции и надежности элементов ИС, а также уменьшение их глубины могут быть достигнуты за счет разработки новых и усовершенствование уже разработанных технологических процессов [1-7]. Например, для уменьшения глубины залегания p-n-переходов может быть использована неоднородность температурного поля, сформированная лазерным или микроволновым отжигами, а также формирование дефектности легируемой структуры. В данной работе рассматривается альтернативный способ уменьшения глубины залегания p-n-переходов. В рамках данного метода рассмотрим трехслойную гетероструктуру (Г), состоящую из подложки (П) и двух эпитаксиальных слоев (ЭС) (см. рис. 1). Ближайший к П ЭС обозначим как ЭС1. Второй ЭС обозначим как ЭС2. Типы проводимости П и ЭС2 считаются известными и одинаковыми (p или n). В ЭС1 с помощью имплантации вводится примесь, формирующая в данном слое второй тип проводимости (n или p). Далее проводится отжиг радиационных дефектов. Толщину ЭС1 и энергию ионов целесообразно подбирать таким образом, чтобы к завершению отжига примесь достигла бы границ раздела между слоями. В таком случае в окрестностях границ раздела между слоями формируются два p-n-перехода. Наличие границ раздела при соответствующим образом выбранных материалах Г позволяет одновременно увеличить резкость p-n-переходов и равномерность распределения примеси в обогащенной области по сравнению с однородным материалом [8,9]. Если в течении отжига радиационных дефектов примесь не достигла границ раздела, целесообразно провести дополнительный отжиг для смещения p-n-переходов на соответствующие глубины. Известно (см., например, [10-12]), что диффузия примеси в материалах после радиационной обработки отличается от диффузии примеси в необработанных материалах. Такая обработка приводит к ускорению диффузии. По этой причине целесообразно провести предварительную радиационную обработку эпитаксиальных слоев перед имплантацией примеси в ЭС1. Это приводит к увеличению разницы между коэффициентами диффузии примеси в ЭС1 и П. В таком случае происходит одновременное увеличение резкости соответствующего p-n-перехода и увеличения равномерности распределения имплантированной примеси. С другой стороны радиационная обработка приводит к ускорению диффузии примеси из ЭС1 в ЭС2, что делает второй p-n-переход более плавным с менее равномерным распределением примеси. Для снижения этих эффектов целесообразно провести микроволновый отжиг радиационных дефектов в ЭС2 для снижения их влияния на распределение имплантированной примеси в p-n-переходе, сформированном между эпитаксиальными слоями. Для наибольшей эффективности микроволнового отжига его частота должна соответствовать толщине скин-слоя, сопоставимой с толщиной ЭС2. Кроме того, микроволновый отжиг дефектов должен проводиться до начала отжига радиационных дефектов в Г. Основной целью данной работы является формирование методики и математическое описание перераспределения примеси и радиационных дефектов в процессе отжига, а также температурного поля. Второй целью данной работы является оптимизации длительности дополнительного отжига примеси в том случае, когда за время отжига радиационных дефектов в Г примесь не достигла границ раздела между ее слоями.
Рис. 1. Трехслойная гетероструктура. В среднем слое приведено
начальное (до отжига) распределение примеси.
Методика анализа
Перераспределение примеси в рассматриваемой гетероструктуре определим путем решения второго закона Фика [1-3]
с граничными и начальными условиями
В соотношениях (1) и (2) введены следующие обозначения: C(x,t) – пространственно-временное распределение концентрации примеси, DС – коэффициент диффузии примеси. Величина коэффициента диффузии определяется свойствами материалов в слоях Г, скорости прогрева и охлаждения Г (в соответствии с законов Аррениуса), а также пространственно-временными распределениями концентраций примесей и радиационных дефектов. Последние две зависимости коэффициента диффузии могут быть аппроксимированы следующим соотношением [2,11]
В данном соотношении DL (x,T) – пространственная (за счет многослойности Г) и температурная (по закону Аррениуса) зависимости коэффициент диффузии; T – температура отжига; P (x, T) – предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [2]; V (x,t) - пространственно-временное распределение концентрации радиационных вакансий; V* - равновесное распределение вакансий. Концентрационная зависимость коэффициентов диффузии подробно обсуждается в [2]. Пространственно-временное распределение радиационных дефектов определялось с помощью следующей системы уравнений [13]
с граничными и начальными условиями
В системе уравнений (4) I(x,t) – пространственно-временное распределение концентрации междоузельных атомов; r =I,V; Dr(x,T) – коэффициенты диффузии междоузельных атомов и вакансий; kI,V(x,T) – параметр рекомбинации дефектов.
Температурное поле описывалось с помощью второго закона Фурье [14]
с граничными и начальным условиями
JT(0,t)=0, JT(L,t)=0, T(x,0)=fT(x). (7)
где T(x,t) – пространственно-временное распределение температуры; n (T)=nass[1 -h exp(-T(x,t)/Td)] – теплоемкость материала (в представляющем наибольший интерес случае, когда температура сопоставима по величине с температурой Дебая или превышает ее, можно считать, что n (T)»nass); Td – температура Дебая [14]; l – коэффициент теплопроводности, величина которого определяется свойствами материалов Г и температурой; температурная зависимость коэффициента теплопроводности в представляющей наибольший интерес области температур может быть аппроксимирована следующим образом: l(x,T)=lass(x)[1+m (Td/T(x,t))j] (см., например, [14]); p(x,t) – выделяющаяся в Г объемная плотность мощности; a(x,T)=l(x,T)/ n (T) – коэффициент температуропроводности.
На первом этапе определим пространственно-временное распределение температурного поля. Для этого следуя [15,16] представим независимый от температуры множитель коэффициента температуропроводности в виде суммы постоянной и переменной составляющих: a ass (x)=a0ass[1+eT gT(x)]. Далее будем искать решение уравнения (6) в виде следующего степенного ряда
Подстановка данного ряда в уравнение (6) позволяет получить систему уравнений для исходного приближения температуры T00(x,t), а также поправочных функций к нему Tij(x,t) (i³1, j ³1) в следующей форме
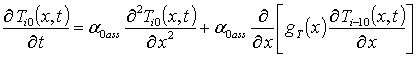 , i ³1
, i ³1
 (9)
(9)
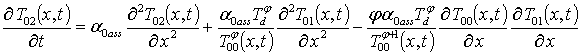
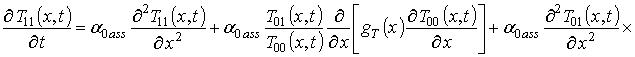

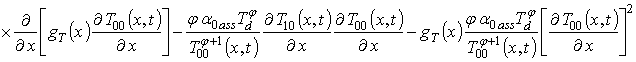 .
.
Подстановка ряда (8) в граничные и начальное условия (7) преобразует их к граничным и начальным условиям для функций Tij(x,t)
T00(x,0)=fT(x), Tij(x,0)=0; 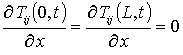 , i ³1, j ³1. (10)
, i ³1, j ³1. (10)
Решение уравнений (9) с условиями (10) приводит к следующему результату
![]()
 ,
,
где cn(x) = cos (p n x/L), enT(t) = exp(-p2n2a0asst/L2);
 , i ³1;
, i ³1;
где ![]() , sn(x) = sin (p n x/L);
, sn(x) = sin (p n x/L);
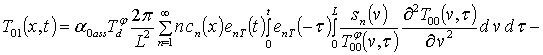
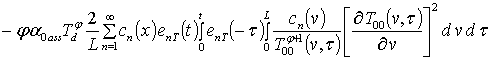 ;
;
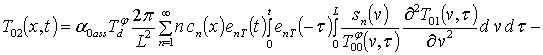
 ;
;

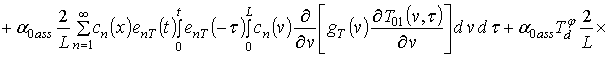

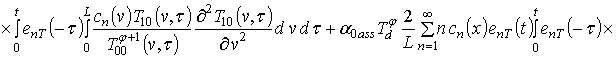
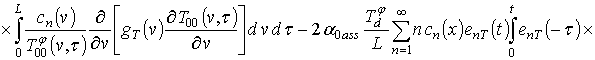
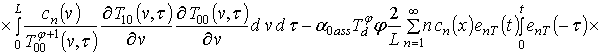
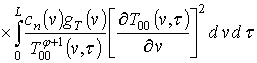 .
.
Для
качественного анализа пространственно-временного распределения температурного
поля, а также для некоторых количественных оценок обычно достаточно его второго
приближения по параметрам, используемым в разложении (см., например, [15,16]).
Аналитические результаты позволили выявить и наглядно проиллюстрировать
основные зависимости. Для уточнения полученных результатов использовались
численные методы. Для определения пространственно-временного распределения
радиационных дефектов, следуя [15,16], преобразуем коэффициенты диффузии и
параметр рекомбинации к следующему виду: Dr(x,T)=D0r[1+ er gr(x,T)]
и kI,V (x,T)=k0I,V[1+z h(x,T)], где D0r и k0I,V – средние значения соответствующих
величин, 0£er <1, 0£z<1, | gr(x,T)|£1, |h(x,T)|£1. Перейдем к следующим безразмерным переменным: c = x/L, ![]() ,
, ![]() . В новых переменных уравнения (4)
принимают вид
. В новых переменных уравнения (4)
принимают вид
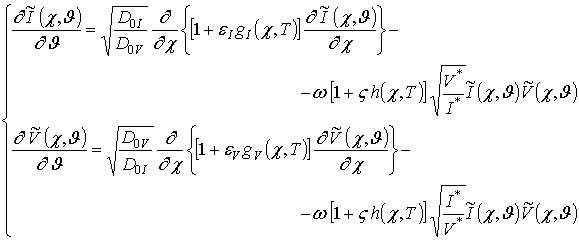 (11)
(11)
Решение уравнений (11) будем искать в виде степенных рядов
Подстановка
данного ряда в уравнения (11) позволяет получить систему уравнений для исходных
приближений концентраций дефектов ![]() , а также поправочных функций к ним
, а также поправочных функций к ним ![]() (i³1, j³1, k³1) в следующем виде
(i³1, j³1, k³1) в следующем виде
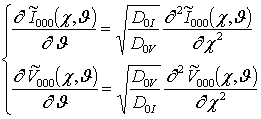 ;
;
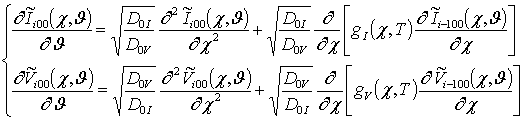 , i ³1;
, i ³1;
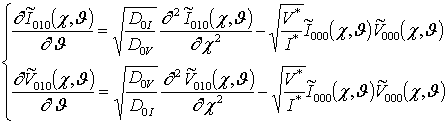 ;
;
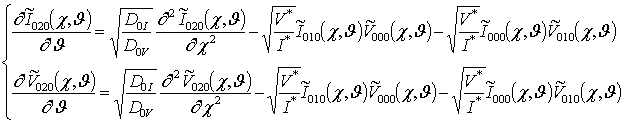 ;
;
 ;
;
 ;
;
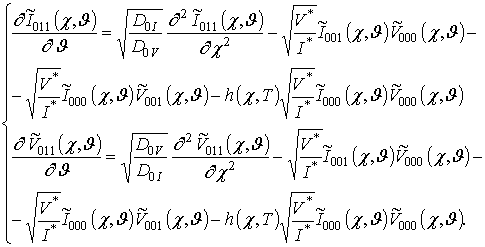
Подстановка
рядов (12) в соответствующие граничные и начальные условия позволяет получить
граничные и начальные условия для искомых функций ![]()
 ;
;  ;
; ![]() , i ³1, j ³1, k ³1.
, i ³1, j ³1, k ³1.
Решениями уравнений (13) являются следующие функции
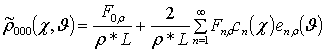 ,
,
где ![]() , cn(c) = cos (p nc),
, cn(c) = cos (p nc), ![]() ,
, ![]() ;
;
 , i ³1;
, i ³1;
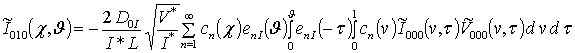 ;
;
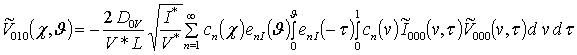 ;
;
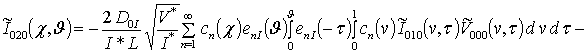
 ;
;
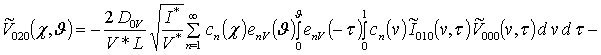
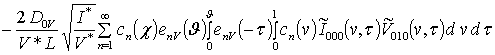 ;
;
![]() ; (14)
; (14)


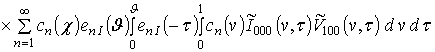 ,
,
где sn(c) = sin (p nc);

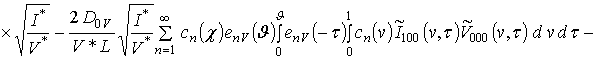
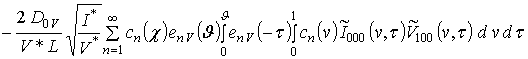 ;
;
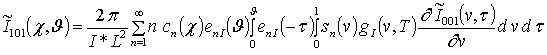 ;
;
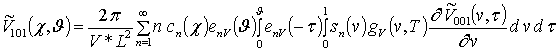 ;
;
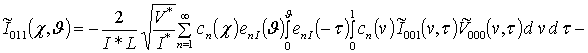
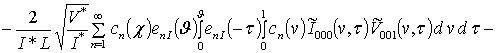
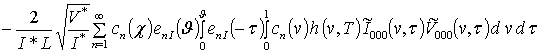 ;
;
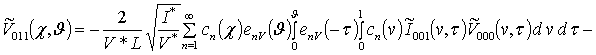
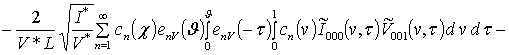
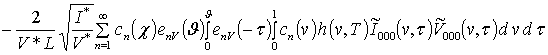 .
.
Анализ пространственно-временного распределения концентраций радиационных дефектов проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно. Далее определим решение уравнения (1). Для этого, следуя [15,16],представим коэффициент диффузии DL (x,T) в виде суммы DL(x,T) =D0L[1+e L gL(x,T)]. Решение уравнения (1) определим в виде следующего степенного ряда
Подстановка данного ряда в уравнение (1) позволяет получить следующую систему уравнений для исходного приближения концентрации примеси C00(x,t), а также поправочных функций к ней Cij(x,t) (i³1, j³1) в следующем виде
 ;
;
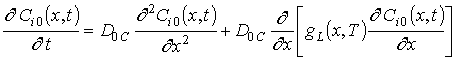 , i ³1;
, i ³1;
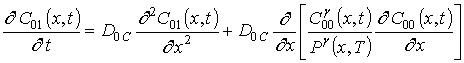 ;
;

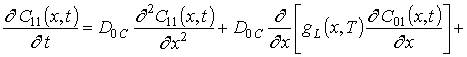

 .
.
Подстановка ряда (15) в соответствующие граничные и начальные условия позволяет получить для искомых функций Cij(x,t)
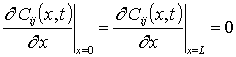 ; C00(x,0)=fC (x); Cij(x,0)=fC (x).
; C00(x,0)=fC (x); Cij(x,0)=fC (x).
Решениями уравнений (16) являются следующие функции
![]() ,
,
где ![]() , enC(t) = exp(-p2n2D0Lt/L2);
, enC(t) = exp(-p2n2D0Lt/L2);
 , i ³1;
, i ³1;
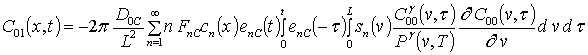 ;
;
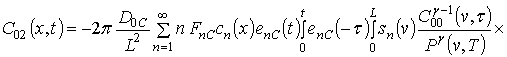
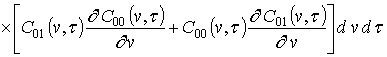 ;
;
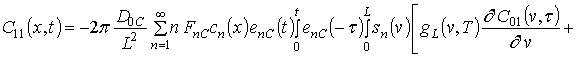
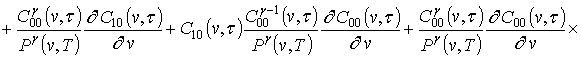
![]() .
.
Анализ пространственно-временного распределения концентрации примеси проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно.
Результаты анализа
В данном разделе проведем анализ перераспределения примеси в рассмотренной Г (рис. 1). Будем считать, что перед введением примеси эпитаксиальные слои прошли радиационную обработку. Далее в ЭС1 была имплантирована примесь. После имплантации проведен микроволновый отжиг радиационных дефектов в ЭС2 для того, чтобы уменьшить их количество. Известно (см., например, [10]), что радиационная обработка материала приводит к ускорению диффузии примеси. По этой причине уменьшение количества радиационных дефектов в ЭС2 приводит к уменьшению коэффициента диффузии примеси в нем. После микроволнового отжига дефектов в ЭС2 с целью уменьшения количества радиационных дефектов в ЭС2 проведем микроволновый отжиг радиационных дефектов в обоих эпитаксиальных слоях. В результате этого отжига уменьшается количество радиационных дефектов в них, а также происходит уширение распределения примеси. В процессе формирования Г и введения примеси необходимо учитывать, что толщину ЭС1 и энергию ионов целесообразно подбирать таким образом, чтобы после окончания отжига примесь достигла бы границ раздела между слоями Г. Если данного достижения не произошло, представляет интерес дополнительный отжиг примеси для данного достижения. Данное достижение после соответствующего подбора материалов слоев Г приводит к увеличению резкости p-n-перехода при одновременном увеличении равномерности распределения примеси в обогащенной ею области [15,16]. Проведение радиационной обработки легируемой области приводит к увеличению разницы между коэффициентами диффузии примеси слоях Г и, как следствие, к увеличению обоих эффектов (и увеличение резкости p-n-перехода, и увеличение равномерности примеси). Наличие неоднородного температурного поля в процессе микроволнового отжига также позволяет увеличить разницу между коэффициентами диффузии примеси. Однако дополнительное увеличение возникает только для p-n-перехода, сформированного между ЭС1 и П, т.к. ЭС2 также подвергается микроволновому отжигу вместе с ЭС1 (в течении отжига радиационных дефектов в ЭС1). По этой причине дополнительной разницы между коэффициентами диффузии примеси в ЭС1 и ЭС2 за счет микроволнового отжига не возникает. Распределение примеси в рассматриваемой Г (рис. 1) после предварительной радиационной обработки эпитаксиальных слоев и их постимпланционного микроволнового отжига приведены на рис. 2.
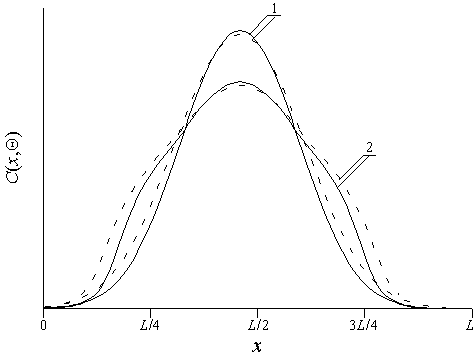
Рис.2. Распределения примеси в трехслойной гетероструктуре. Кривые 1 – распределения при-меси в однородном материале. Кривые 2 - распределения примеси в трехслойной структуре.
Далее проведем оптимизацию длительности дополнительного отжига примеси в случае, когда примеси не достигает границ раздела Г. Если длительность отжига мала, получаем слишком неоднородное распределение примеси. Если длительность отжига велика, распределение примеси становится слишком равномерным (см. рис. 3). Искомая длительность определялась, следуя [8,9,14,16], из условия минимума среднеквадратической ошибки между реальным распределением концентрации примеси C(x,t) и ее скачкообразной аппроксимацией y (x) (см. рис. 3)
![]() .
(17)
.
(17)
Результат минимизации приведен на рис. 4 в зависимости от нескольких параметров.
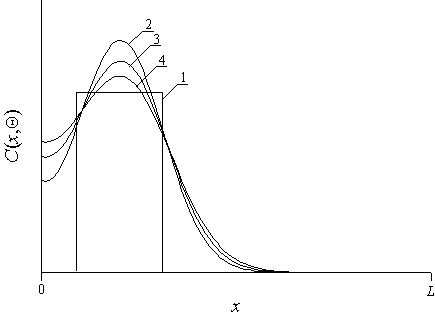
Рис. 3. Кривая 1 – идеализированное распределение примеси; кривые 2-4 – реальные распределения примеси в различные моменты времени, растущие с номером кривых.
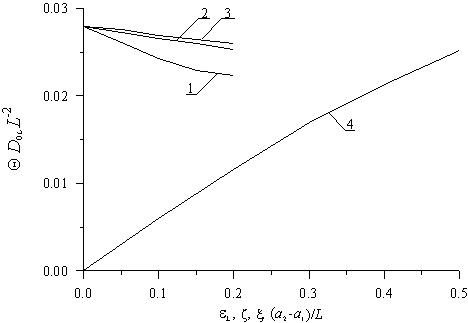
Рис. 4. Зависимость безразмерного компромиссного времени отжига J = QD0/L2, полученного из условия минимума функционала (17), от различных параметров ТС. Кривые 1-3 – зависимости J соответственно от eL, z и x при нулевых значениях остальных двух параметров и (a2-a1)/L=1/2. Кривая 4 – зависимость J от a/L при e =z=x=0.
Заключение
В данной работе рассмотрен способ увеличения компактности распределения примеси в имплантационном биполярном транзисторе, а также ее равномерности в легированной области путем использования предимплантационной радиационной обработки легируемой области и постимплантационного микроволнового отжига радиационных дефектов.
Данная работа поддержана грантом президента России (проект № МК-548.2010.2).
Литература
[1] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons,1983,894p.
[2] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.
[3] В.И. Лачин, Н.С. Савелов. Электроника. Ростов-на-Дону: Феникс, 2001. 446 с.
[4] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян. ФТП. 2002. Т.36 (5). С. 611-617.
[5] Ю.М. Покотило, А.Н. Петух, В.В. Литвинов, Письма в ЖТФ Т. 29 (19), С. 26-30 (2003).
[6]
T. Ahlgren, J. Likonen, J. Slotte, J. R![]() is
is![]() nen, M. Rajatore, J. Keinonen. Phys. Rev. B.
1997. V.56, (8). P. 4597-4603.
nen, M. Rajatore, J. Keinonen. Phys. Rev. B.
1997. V.56, (8). P. 4597-4603.
[7] Н.И. Волокобинская, И.Н. Комаров, Т.В. Матюхина, В.И. Решетников, А.А. Руш, И.В. Фалина, А.С. Ястребов. ФТП. 2001. Т.35 (8). С. 1013-1017.
[8] E.L. Pankratov. J. Appl. Phys. 2008. Vol. 103 (6). P. 064320-064330.
[9] E.L. Pankratov. Phys. Lett. A. 2008. Vol. 372 (11). P. 1897-1903.
[10] В.В. Козловский. Модифицирование полупроводников пучками протонов. Санкт-Петербург: “Наука”, 2003. 268 с.
[11] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. М.: Энергия. 1975. 130 с.
[12] Ryssel H., Ruge I. Ion implantation. B.G. Teubner, Stuttgart, 1978. 360 с.
[13] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.
[14] К.В. Шалимова. Физика полупроводников. М.: Энергоатомиздат, 1985. 391 с.
[15] E.L. Pankratov. Phys. Rev. B. 2005. V.72 (7). P. 075201-075208.
[16] E.L. Pankratov, B. Spagnolo. The Eur. Phys. J. B. 2005. V. 46 (1). P. 15-19.