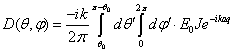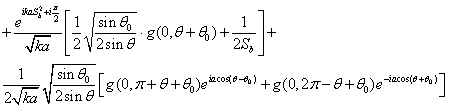Асимптотическая теория биконической антенны
В. А. Калошин, Е. С. Мартынов
Институт радиотехники и электроники им. В.А.Котельникова РАН
Получена 9 сентября 2011 г.
Аннотация. Получены две асимптотические формулы для диаграммы направленности биконической антенны. Одна из формул справедлива вблизи оси, другая вдали от оси антенны. Проведено сравнение результатов расчета по этим формулам диаграммы направленности биконической антенны с соответствующими результатами, полученными методом интегральных уравнений. Показано, что развитая асимптотическая теория позволяет вычислять диаграмму направленности практически во всем диапазоне углов наблюдения.
Ключевые слова: коротковолновая асимптотика, свехширокополсные антенны, биконические антенны.
Abstract. The two asymptotic formulas for a biconical antenna radiation pattern have been obtained. One of the formulas is valid near the axis, the other - away from the axis of the antenna. The calculation results with using these formulas for biconical antenna radiation pattern are compared with the corresponding results obtained by the method of integral equations. It is shown that the developed asymptotic theory allows to calculate the radiation pattern practically in the entire range of observation angles.
Keywords: wave-short asymptotics, ultrawideband antennas, biconical antennas.
Биконические вибраторы широко используются в качестве сверхширокополосных антенн УКВ и СВЧ диапазонов электромагнитных волн. Исследованию этих антенн посвящено большое количество научных работ. Для анализа биконических антенн используются различные численные и численно-аналитические методы: метод собственных функций [1], конечных элементов [2] и конечных разностей во временной области [3]. При этом возникают трудности при анализе антенны в высокочастотной части ее диапазона из-за большого порядка соответствующих матриц. Для вычислений в этой области в работе [2] развит асимптотический метод анализа диаграммы направленности и коэффициента отражения биконической антенны. Формулы, приведенные в [2], позволяют рассчитывать диаграмму направленности антенны только вдали от ее оси. Изложенная ниже теория позволяет проводить такой расчет практически для всех углов наблюдения.
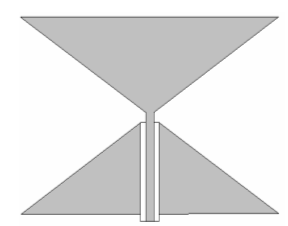
Рис.1. Биконическая антенна.
Сечение биконической антенны показано
на рис.1. Приближение Кирхгофа для электрического поля, излученного
биконической антенной, в сферической системе координат r, 
, 
выражается
через интеграл
,
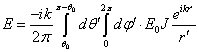(1)
где 
- амплитуда электрического
поля основной моды биконуса, 2
угол при вершине конуса, a – длина образующей конуса,
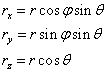
Выражение
для 
можно преобразовать к виду
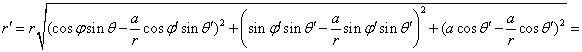
, (2)
где
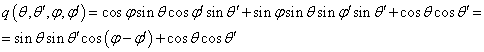
Подставив выражение (2) для r` в интеграл (1), получим
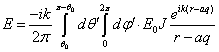
В
дальней зоне 
, где 
- диаграмма антенны.
Учитывая, что в дальней зоне 
, получаем для диаграммы выражение
Интеграл (3) будем вычислять
методом стационарной фазы. Начнем с вычисления внутреннего интеграла (по 
)
Нетрудно показать, что 
Отсюда получаем уравнение для точек стационарной
фазы 
, которое имеет два решения 
и 
.
Вычислим вклад в интеграл первой точки .
Учитывая, что вторая производная в стационарной
точке
, получаем
Аналогично
для второй точки, получаем
Перейдем
к интегрированию по 
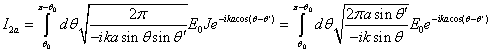
Сократим
на 
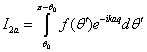
Вычислим
вклад в стационарной точке 
,
где 
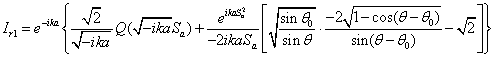
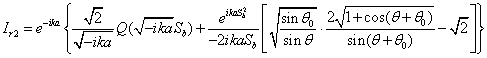
В
итоге 
,
где 
Сократим
в 
и 
на 
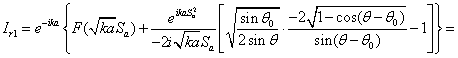
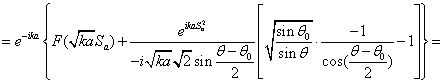
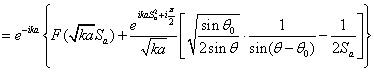
Аналогично
для
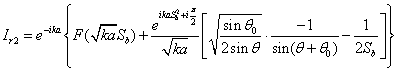
Поделим
на 
и для получим
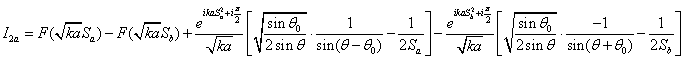
Для уточнения приближения Кирхгофа заменим
дифракционные коэффициенты, полученные из приближения Кирхгофа 
, на дифракционные коэффициенты для краевой
волны из решения Зоммерфельда на клине
,
где
, 
,
- дополнительный угол клина
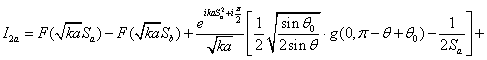
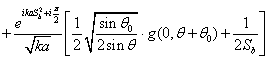
Коэффициент 
появляется
из-за совпадения границ света-тени проходящего и отражённого луча. В итоге
получим:
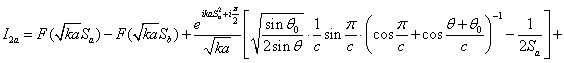(4)
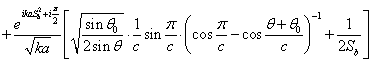
Вычислим
теперь интеграл во второй стационарной точке
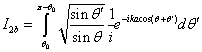(6)
В силу осевой симметрии антенны ограничимся
рассмотрением углов 
. При этом стационарная точка
лежит вне пределов интегрирования и вклад в интеграл (6) дают только края
интегрирования. В результате, получаем
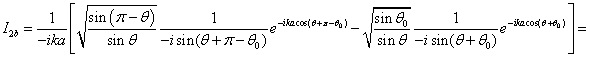(7)
Вспомним теперь, что в мы сокращали на и подставив дифракционные коэффициенты,
получим
=
(8)
Суммируя (4) и (8), получаем
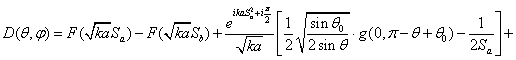
Полученная формула (9) несправедлива вблизи оси антенны. Для получения формулы, справедливой в этой области поменяем порядок интегрирования в интеграле (3)
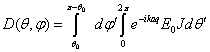
Далее проинтегрируем по методом
стационарной фазы, полагая, что для точек наблюдения вблизи оси стационарные
точки не находятся внутри пределов интегрирования. В результате, получаем
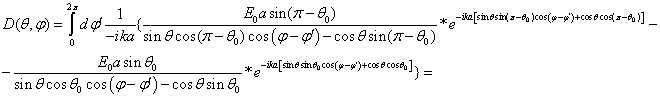
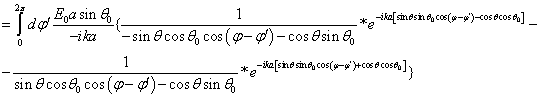
Далее представим
,
где
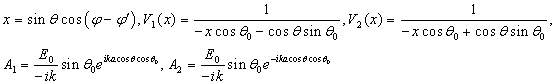
Разложим 
в
ряд Тейлора вблизи точки
. В результате, получим
, где 
- l
производная функции Бесселя.
Выразим через 
и 
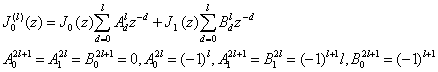(10)
где
Подставляя
(10) в 
, получим
Для первого члена асимптотики
,
(11)
где
В
нашем случае 
и 
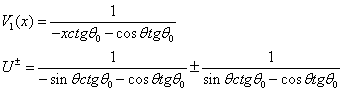
На рис. 2 приведены
результаты расчета диаграммы направленности биконической антенны по полученным
формулам. Синим пунктиром показаны результаты расчета по формуле (9) , зеленым
– по формуле (11) . Красной сплошной линией показана диаграмма направленности,
рассчитанная методом интегральных уравнений [4] . Как видно из рисунка,
асимптотика (11) хорошо совпадает с численным решением в области 160° < < 20°, а асимптотика (9) – в области
145° > > 35°. Таким образом, совокупность
полученных формул дает возможность вычисления диаграммы направленности
практически во всей области изменения угла .
D()
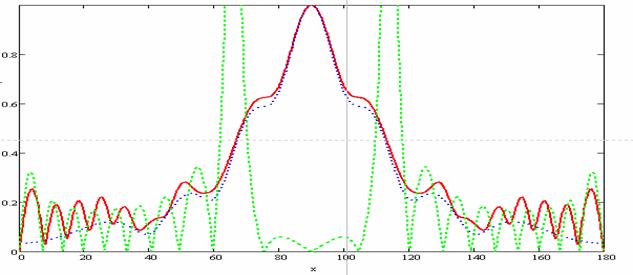
Рис.2. Диаграмма направленности.
Работа выполнена при поддержке РФФИ, проект № 10-07-00705-а.
Литература
1. М.Н. Макурин, Н.П. Чубинский, Расчет характеристик биконической антенны методом частичных областей, Радиотехника и электроника, 2007, т. 52, №10, с. 1199–1208.
2. В.А. Калошин, Е.С. Мартынов, Е.А. Скородумова, Моделирование биконической антенны в широкой полосе частот, Труды III Всероссийской конференции "Радиолокация и радиосвязь", М.,2009 г., т.1, с. 97-101.
3. В.И. Кошелев, А.А. Петкун, М.П. Дейчули, Ш. Лю, Частотные и временные характеристики конических ТЕМ антенн, Труды IV Всероссийской конференции "Радиолокация и радиосвязь", М., 2010 г., с. 336-340.
4. А.Г. Давыдов, Ю.В. Пименов, О возможностях новой версии программного комплекса EDEM, Тезисы докладов и сообщений I Международной научно-технической конференции «Физика и технические приложения волновых процессов», Самара, 10–16 сентября 2001 г., т.1.