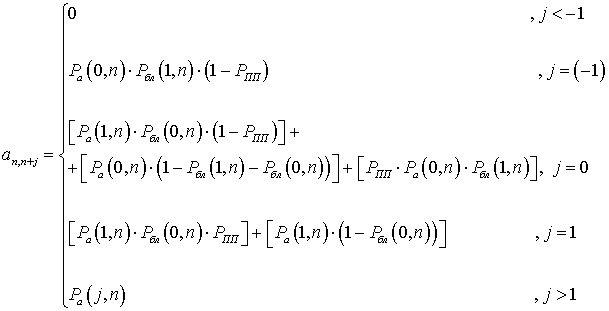УДК 623.624
Подавление пакетных радиосетей со случайным множественным доступом за счет дестабилизации их состояния
С. И. Макаренко
Военно-космическая академия имени А. Ф. Можайского
Получена 2 сентября 2011 г.
Аннотация. Рассмотрен способ подавления радиосетей основанный на внутренних особенностях их функционирования, за счет перевода сети в нестабильное состояние работы путем воздействия преднамеренных помех. Рассмотрены возможности подавления радиосетей случайного множественного доступа на основе протоколов S-ALOHA и CSMA/CD.
Ключевые слова: радиоэлектронное подавление, радиоэлектронная борьба, радиосеть, случайный множественный доступ, протокол ALOHA, протокол CSMA/CD.
Abstarct. The article contains the method of radio countermeasures for radionet based on internal specificity their work. The radio countermeasures is maken by changing the radionet state to non-stable by means of radio noise using. It is reviewed radio possibilities of radio networks with S-ALOHA and CSMA/CD access algorithms.
Keywords: the radio electronic countermeasures, the electronic warfare, the radio networks, the random multiple access, the ALOHA algorithm, the CSMA/CD algorithm.
Обоснование возможностей подавления радиосетей за счет дестабилизации их состояния
В настоящее время в составе сетей связи (СС) специального назначения [1] активно ведется переход на пакетные радиосети (ПРС), которые являются основой для системы информационного обеспечения боевых действий в сетецентрических войнах нового поколения [2-4]. В связи с тем, что ПРС являются основой системы управления боевыми действиями, ее подавление приведет к снижению оперативности и надежности управления и как конечный результат – невозможности достижения целей проводимой операции.
Известно большое количество работ (в частности монографии Владимирова В. И., Борисова В. И. [5, 6]) рассматривающих подавление радиосетей за счет энергетического превосходства средств радиоэлектронного подавления (РЭП) над используемой линией радиосвязи, либо за счет использования специальных алгоритмов работы РЭП при постановке преднамеренных помех (ПП). Вместе с тем, еще в начальных работах по проектированию первых пакетных СС Л. Клейнрока, Д. Берстсекаса и Р. Галлагера [7, 8] указывается, что пакетным СС использующие для передачи пакетов общий канал по методу случайного доступа свойственна нестабильность функционирования и такие СС требуют коррекции при большом времени непрерывной работы. Таким образом, возможно подавление сети являющейся радиоканалом множественного доступа путем периодического воздействия ПП за счет использования специфических свойств метода доступа. Данный подход при подавлении ПРС был впервые указан Бабусенко С. И. в работах [9, 10] и рассмотрен далее.
Полносвязная ПРС представляет собой пространственно-распределенную структуру. Каждый из ее абонентов, представляющий собой узел связи, имеет возможность передачи пакетов без промежуточных ретрансляций. В ПРС используется общий радиоканал который разделяется между абонентами по времени, причем доступ к каналу осуществляется случайно. Введем понятие блокированного абонента (узла) – абонент, ожидающий передачи вновь сформированного или ранее неправильно переданного пакета.
Как показано работах [7, 11] число блокированных абонентов, однозначно определяет устойчивое состояние сети. Устойчивое состояние характеризуется работой с малым временем задержки и наибольшей производительностью. Для неустойчивого состояния характерны необратимый рост времени задержки и снижение производительности сети. Это обусловлено тем, что при случайном характере поступления покетов для передачи даже без воздействия ПП возможна ситуация, когда число вновь сформированных пакетов превышает возможности канала по успешной передаче.
Введем обозначения и сокращения:
М – количество абонентов сети;
L - показатель среднего сноса сети который интерпретируется как разность между интенсивностью возникновения новых пакетов за цикл передачи и интенсивностью ухода из сети успешно переданных пакетов;
n – количество блокированных абонентов, то есть абонентов ожидающих передачи вновь сформированного или ранее неправильно переданного пакета;
Р1 – вероятность передачи пакета абонентом с первой попытки;
Рповт – вероятность передачи пакета абонентом при повторной попытке;
РПП – вероятность воздействия преднамеренной помехи на канал связи;
Рa(j, n) – вероятность успешной передачи в очередном такте j-ым количеством активных абонентов при n блокированных абонентах
Рбл(j, n) – вероятность успешной передачи в очередном такте j-ым количеством блокированных абонентов при n числе блокированных абонентах;
Рa(j) – вероятность передачи в текущем такте j активных пользователей;
Рn - вероятность того, что после свободного такта начнет передачу хотя бы один из абонентов, при условии что имеется n блокированных абонентов;
Pj – вероятность нахождения канала связи в состоянии Zj без учета длительности нахождения в каждом состоянии;
PZ j - конечные вероятности перехода канала связи в состояние Zj;
λn – интенсивность «нарастания» количества блокированных абонентов из-за коллизий и воздействия помех;
µn – интенсивность «рассасывания» блокированных абонентов в результате успешных передач;
tПП – длительность воздействия преднамеренной помехи на канал связи;
λ1 – интенсивность пакетов поступающих в канал связи впервые;
G - суммарная интенсивность пакетов поступающих в сеть;
S – относительная пропускная способность канала связи (нормированная к единице);
Сjn - сочетания j из n;
SПП - относительная пропускная способность канала связи при воздействии помехи;
Tзад – задержка при передаче пакета по каналу связи;
ТZ j – мат. ожидание времени нахождения канала в Zj-ом состоянии выраженное в количестве тактов;
τ – длительность такта с сети с синхронным МДПН;
td – длительность захвата канала абонентом в сети с синхронным МДПН;
dmax – расстояние между максимально удаленными абонентами сети с синхронным МДПН;
с – скорость распространения радиоволн.
Для качественного рассмотрения эффекта воздействия на подобную ПРС примем следующие общие для рассматриваемых базовых моделей допущения [8]:
- система имеет в своем составе ПРС, состоящую из М однотипных узлов-абонентов и средство РЭП являющееся источником ПП;
- все элементы системы синхронизированы и могут начать работу лишь в тактовые моменты времени tq;
- если более одного абонента одновременно начинают передачу, то коллизия (столкновение передач в общем радиоканале от разных абонентов) и абонент-приемник не получает никакой информации, аналогично - в случае действия ПП;
- неуспешно переданный пакет передается абонентом повторно в один из последующих моментов до его успешной передачи;
- пакет, передаваемый абонентом впервые, передается с вероятностью Р1 повторная передача осуществляется с вероятностью Рповт > Р1, а ПП воздействует на канал с вероятностью РПП;
- в конце каждого цикла передачи абонент, осуществляющий ее, по каналу обратной связи, не поверженному влиянию помех, оповещается об успешной передаче или искажении пакета;
- все абоненты и узлы имеют единственное место (буфер) для хранения пакета.
Принятые допущения идеализируют модель многостанционного доступа к общему радиоканалу, однако как показано в [12], принятая модель достаточно адекватно отражает реальные процессы в канале множественного доступа.
Процесс передачи информации в канале радиосвязи со случайным доступом можно представить как процесс обслуживания пакетов поступающих в систему впервые и повторно. В зависимости от взаимного расположения абонентов ПРС с относительной пропускной способностью S, вероятности успешной передачи Р1 и интенсивности поступления пакетов, поступивших впервые λ1, можно выделить несколько ситуаций определяющих поведение вышеуказанной системы (см. рис. 1).
Поведение системы изменяется в пределах точек nS, nk, nnS являющихся точками равновесия [7], так как интенсивность успешного обслуживания пакетов в них равна вновь образованной нагрузке. Первая точка nS является стабильной (устойчивой) по отношение к стохастическим флуктуациям числа блокированных абонентов n в пределах от 0 до nk, и система всегда смещается к nS. Точка nnS является финальной при изменениях n в области от nk до nnS. Рассмотренные точки соответствуют: nS – стабильному (рабочему) состоянию ПРС с малой задержкой и высокой производительностью, nnS – нестабильному (устойчивому нерабочему) состоянию, которое характеризуется малой производительностью и большой задержкой. При различных параметрах Р1, M, Рповт и РПП можно выделить стабильные ПРС и нестабильные, в противном случае [13].
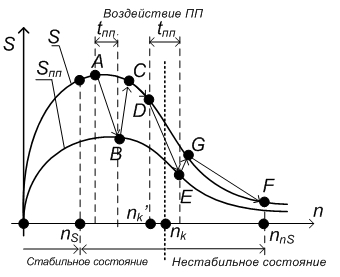
Рис. 1. Изменение состояния ПРС под воздействием ПП
Практически стабилизация канала достигается за счет уменьшения вероятности повторной передачи Рповт, что всегда влечет возрастание времени задержки Tзад [13]. В силу данной причины параметры передачи Р1 и Рповт выбирают такими, чтобы обеспечить наименьшую задержку, а также уменьшить возможность перехода сети в неблагоприятное (нестабильное) состояние. Как показали исследования [7] в правильно настроенной сети, без влияния ПП время перехода в нестабильное состояние превышает десятки часов, что удовлетворяет в большинстве случаев практического применения. Необходимо отметить, что переход ПРС в нестабильное состояние может быть обусловлен дополнительным влиянием ПП (РПП ≠ 0). При их воздействии производительность сети понижается, то есть сужается область возможных статистических флуктуаций числа блокированных абонентов n вокруг рабочей точки nS и расширяется пространство в районе точки насыщения nnS, что увеличивает шансы перехода сети в нестабильное состояние.
Предположим, что в ПРС при РПП = 0 число блокированных абонентов находится около точки стабильного состояния nS (точка А на рис. 1). В результате воздействия ПП с вероятностью РПП производительность сети снижается до SПП (точка В). После прекращения действия ПП производительность ПРС уменьшается за счет увеличения количества временно блокированных абонентов (траектория B-С-D). При повторном воздействии ПП, производительность сети снова снизится и состояние сети сместится в точку E которая лежит правее точки неустойчивого равновесия nk. В результате после каждого цикла передачи количество абонентов, имеющих пакеты для повторной передачи в сети возрастает, и состояние сети смещается в направлении точки nnS. Воздействуя на сеть ПП в течение требуемого времени tПП, можно достичь состояния, когда число абонентов, требующих повторной передачи, превысит границы устойчивости n > nk. В этом случае, даже после прекращения излучения ПП, изменение состояния системы будет осуществляться по траектории Е-G-F к устойчивой точке F за счет коллизий в ПРС.
С учетом приведенной модели эффект нестабильного функционирования канала заключается в том, что благодаря наличию коллизий при определенном числе абонентов, ожидающих канал для повторной передачи, среднее количество успешных передач за цикл меньше среднего числа неуспешных передач за это же время. Данное обстоятельство приводит к тому, что после каждого такта работы происходит нарастание абонентов, требующих повторной передачи. Таким образом, данный способ подавления может быть осуществлен низкоэнергоемкими средствами РЭП за счет внутренних особенностей функционирования сети и применим ко всем ПРС использующим случайный множественный доступ абонентов в режиме разделения времени. Таким образом, указанный способ может быть применен к ПРС на основе протоколов IEEE 802.3, IEEE 802.11, а так же ко всем разновидностям доступа к каналу на основе протоколов ALOHA и CSMA/CD.
Количественно оценить стабильность функционирования сети можно по показателю среднего сноса L (n, PПП), n = 0..M. [14, 15]. Он интерпретируется как разность между интенсивностью возникновения новых пакетов за цикл передачи и интенсивностью ухода из сети успешно переданных пакетов при условии, что в данный момент имеется n ожидающих повторной передачи узлов. Сеть работает нестабильно, если снос примет положительное значение [13]:
где an,k определяется вероятностью перехода количества абонентов, ждущих повторной передачи из n состояния в k и вычисляется согласно рассмотренной ниже системы (3).
Подавление пакетных радиосетей с методом доступа S-ALOHA
В сетях с S-АLOHА передача пакетов узлами происходит в любой тактовый момент, то есть действия всех абонентов полностью независимы [7, 13].
Для описания процесса изменения числа абонентов ожидающих повторной передачи (блокированных абонентов) в полносвязной ПРС с доступом типа S-АLOHА воспользуемся марковской моделями [7, 13, 16], модифицированными с учетом влияния ПП.
Предполагается, что каждый абонент находится в одном из двух состояний «готовность» и «блокирован». В состоянии «готовность» абонент генерирует пакеты с интенсивностью λ1. Если первая передача пакета, с вероятностью Р1 прошла успешно, абонент остается в режиме готовности, после чего возможна генерация нового пакета. Если передача пакета в вероятностью (1- Р1), в результате коллизии или воздействия ПП прошла неудачно, то абонент переходит в режим «блокирован» и планирует повторную передачу с вероятностью Рповт (рис. 2). Находясь в режиме «блокирован», абонент не генерирует новых пакетов.
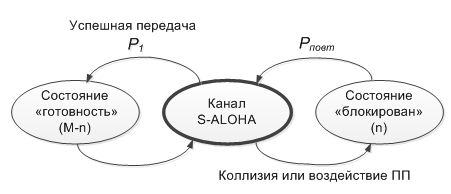
Рис. 2. Модель переходов состояний абонента в сети S-ALOHA
Учитывая, что длительность сегмента передачи составляет длительность пакета – τп = ti – ti-1, последовательность состояний ПРС с определенным количеством заблокированных абонентов в тактовые моменты времени изменяются согласно вероятностям переходов по цепи Маркова (рис. 3) с матрицей переходов (2). Переходы в состояние с меньшим номерам возможны лишь в соседние состояние, так как за такт может быть передан один пакет. Переход из состояния 0 в состояние 1 отсутствует, так как если бы все абоненты находились в состоянии готовности и один абонент сгенерировал пакет, он не может своими действиями вызвать конфликт. Так как число блокированных абонентов n не может превышать количество абонентов М, то Марковская цепь конечна, а так как все состояния связаны, то цепь имеет стационарное устойчивое состояние.
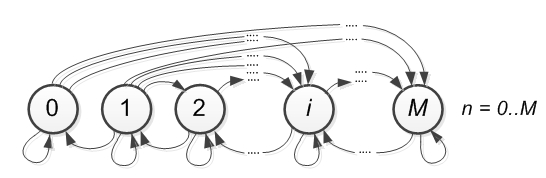
Рис. 3. Марковская цепь изменения количества n блокированных абонентов в сети с алгоритмом S-ALOHA
Число изменения блокированных узлов за цикл передачи j определяется следующим образом (см. рис. 2):
- уменьшатся на 1, если не произойдет искажения пакета помехой, либо коллизий при передаче пакета;
- не изменится, в случае успевшной передачи пакета неблокированным абонентом или в случае неуспешной попытки передачи блокированным абонентом;
- увеличиться на 1, если неудачно закончится передача активного абонента;
- увеличится на j в случае одновременной попытки передачи j абонентов.
В этом случае, матрицу переходов указанного Марковского процесса
можно представить в виде условных вероятностей того, что на очередном цикле количество блокированных абонентов станет n+j при условии, что на предыдущем цикле их было n :
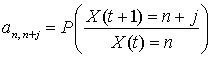 ,
,
где
В системе (3) приведенные вероятности имеют следующий смысл:
Рa(j, n) – вероятность успешной передачи в очередном такте j-ым количеством активных абонентов при n блокированных абонентах:
Рa(j, n) = СjM-n (1- Р1)M-n-j (Р1) j ; (4)
Рбл(j, n) – вероятность успешной передачи в очередном такте j-ым количеством блокированных абонентов при n числе блокированных абонентах:
Рбл(j, n) = Сjn (1-Рповт)n-j (1-Рповт) j . (5)
В выражениях (4) и (5) запись Сjn означает сочетания j из n.
Подставив в выражение (1) значение an,k, после ряда преобразований получим:
L(n, PПП) = λn - µn (6)
где: λn – интенсивность «нарастания» количества блокированных абонентов n из-за коллизий и действия помех, определяемая как:
![]()
![]() ;
;
µn – интенсивность «рассасывания» блокированных абонентов в результате успешных передач, определяемая как:
µn = Ра(0,n) Рбл(1,n) (1-РПП).
Качественная зависимость коэффициента сноса L(n, PПП) от числа блокированных абонентов n и вероятности воздействия помех PПП приведена на рис. 4.
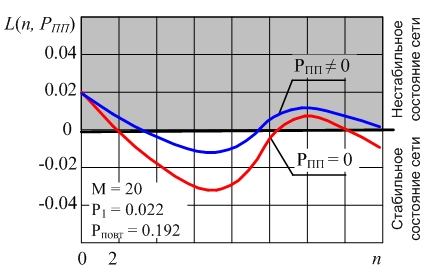
Рис. 4. Качественная зависимость коэффициента сноса L(n, PПП) от числа блокированных пользователей n и вероятности воздействия помех PПП
Как видно при наличии помех зона положительных значений коэффициента сноса L (n, PПП) увеличивается, что соответствует увеличению области нестабильного функционирования СРС.
Решая уравнения для конечного стабильного состояния сети, найдем конечные вероятности Pn* для каждого количества блокированных абонентов n [17]:
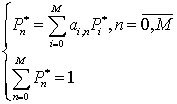 (7)
(7)
Откуда можно получить математическое ожидание числа успешных передач, этот показатель будет определять S - относительную пропускную способность канала функционирующего по алгоритму S-АLOHА
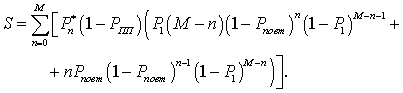 (8)
(8)
Среднее время задержки Tзад передачи пакета, выраженное в количестве попыток передачи, рассчитаем по формуле Литтла [18]:
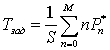 . (9)
. (9)
Математическое ожидание mn и дисперсия Dn количества блокированных абонентов в стационарном режиме будет определяться как:
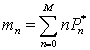 , (10)
, (10)
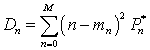 . (11)
. (11)
Подавление пакетных радиосетей с методом доступа CSMA/CD
Метод доступа Carrier sense multiple access with collision detection (CSMA/CD) – случайный множественный доступ с проверкой несущей (МДПН), описываемый стандартом IEEE 802.3, получил широкое распространение в радиосетях типа Wi-Fi, а так же с незначительными доработками в качестве стандарта МАС-подуровня (media access control – управление доступом к устройствам) канального уровня OSI сетей специального назначения.
В синхронной версии МДПН длительность такта τ определяется временем распространения радиосигнала по сети с радиусом dmax:
![]() ,
,
где: dmax – расстояние между максимально удаленными абонентами СС; с – скорость распространения радиоволн.
Алгоритм работы абонента представляет собой следующую последовательность действий:
1. Если канал свободен, то абонент передает пакет в течение необходимого количества тактов, длительностью mτ.
2. Если канал занят, то абонент откладывает свою передачу на более позднее время, в соответствии со случайным распределением задержки td повторной передачи. Когда наступает это время, абонент вновь проверяет канал и повторяет описанный алгоритм.
Процесс генерации пакетов абонентами представляет собой стационарный пуассоновский процесс с суммарной интенсивностью λ1. В процессе функционирования в составе сети абонент может перейти в блокированное состояние в результате коллизии (при наложении одновременных передач различных абонентов), занятости канала связи, а так же в случае искажения текущей передачи в результате воздействия ПП. Длительность цикла передачи случайна (см. рис. 5) и определяется задержкой передачи для «захвата» канала td , временем передачи τm, и наличием «защитного такта» перед следующей передачей длительностью τ.
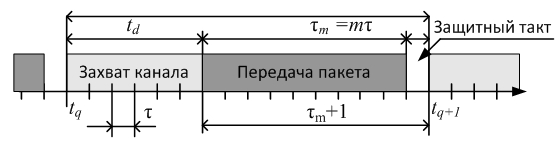
Рис. 5. Цикл передачи в сети с методом доступа МДПН
Изменение числа блокированных абонентов не является Марковским процессом и для его описания используем метод Кендала [18]. Введем допущение, что на длительности захвата (прослушивания) канала td число блокированных абонентов n не изменилось, если в следующий такт хотя бы один абонент начнет прослушивать канал, для осуществления передачи, состояние занятости абонентов измениться аналогично каналу с алгоритмом ALOHA:
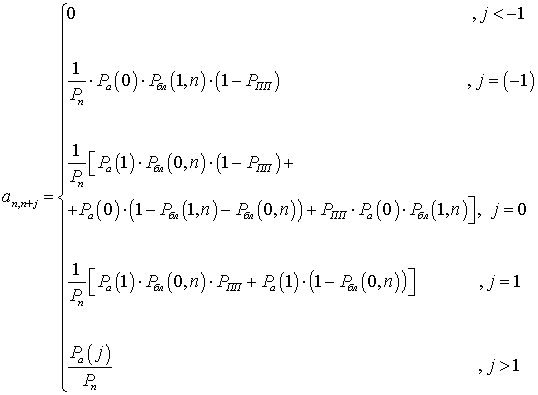 (12)
(12)
где: Ра(j) – вероятность передачи в текущем такте j активных пользователей:
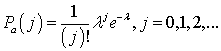 ;
;
Рn – вероятность того, что после свободного такта начнет передачу хотя бы один из абонентов, при условии что имеется n блокированных абонентов:
![]() .
.
За время передачи любой из абонентов может попытаться получить доступ к каналу и обнаружить, что он занят. В таком случае такие активные абоненты перейдут в состояние «блокирован», а матрица переходов состояния таких абонентов определяется числом требований поступивших за время обслуживания текущей передачи длительностью τm+1:
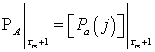 , (13)
, (13)
где
 .
.
В этом случае матрица вероятностей переходов числа блокированных абонентов P = [ Pn,j*] за цикл передачи (td +τm+1) будет иметь вид:
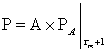 (14)
(14)
Элементы матрицы A = [an, n+j] определяются в соответствии с системой (12).
Найдем значение сноса L(n, PПП) для сети с МДПН из выражения (1) с учетом выражений (13) и (14):
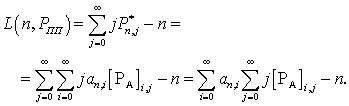 (15)
(15)
После упрощения выражения получим:
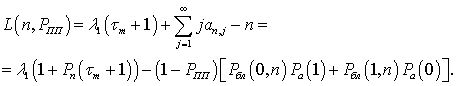 (16)
(16)
При допущении о большом количестве равномерно «слабых» абонентов в сети n→∞, крайнее выражение возможно упростить с учетом преобразований:
![]() ,
,
![]() . (17)
. (17)
Тогда выражение (16) примет вид:
![]() , (18)
, (18)
где G = λ1+nPповт - интенсивность трафика поступающего в канал связи.
На рис. 6 приведены качественные зависимости, построенные для сноса L(G, PПП) в соответствии с (18) для различных значений PПП и интенсивности трафика в канале G.
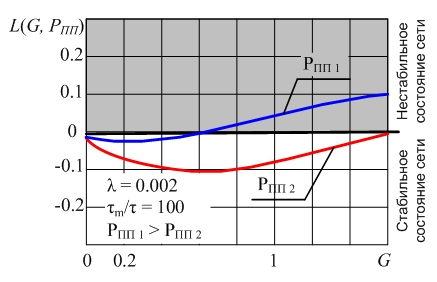
Рис. 6. Зависимость интенсивности сноса от интенсивности трафика в сети с МДПН
Для получения относительной пропускной способности сети и времени задержки используем теорию Марковских процессов. Средняя пропускная способность сети с МДПН есть относительное время пребывания сети в состоянии успешной передачи, то есть данный показатель может быть найден при анализе состояний такой сети [15]. Из-за произвольного распределения длительности циклов передачи процесс смены состояний на является Марковским, в связи с чем для его описания используем теорию вложенных полумарковских процессов [17-19].
Пространство состояний канала связи приведен на рис. 7. Переход из одного состояние в другое определяется интенсивностью потока пакетов на передачу, из-за чего происходит скачкообразное изменение состояний Z0 → Z1 → Z2 → Z0 → Z1 → Z3 →… в произвольные моменты времени.
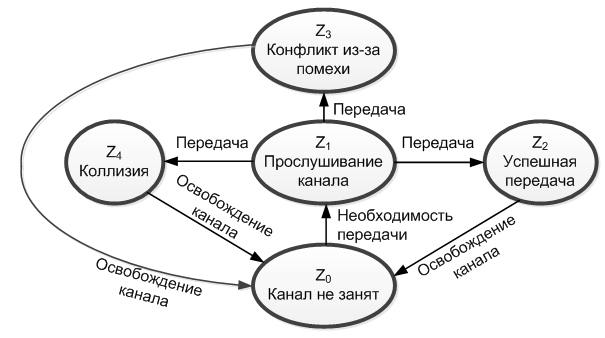
Рис. 7. Пространство состояний канала связи в сети с методом доступа МДПН
Определим вероятности перехода между состояниями:
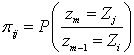 ,
,
а так же условные функции распределения вероятностей переходов Zi → Zj на длительности цикла передачи:
![]() .
.
Марковский процесс полностью определяется вероятностью начального состояния (Z1) матрицей вероятностей перехода [πij] для i, j = 0..4 и матрицей функций распределения [ Fij(t) ]. Для стационарного режима функционирования сети, существует стационарное решение для Марковской цепи. могут быть определенны как [17]:
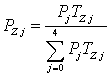 , (18)
, (18)
где: ТZ j – мат. ожидание времени нахождения абонента в Zj-ом состоянии выраженное в количестве тактов; Pj –вероятность нахождения абонента в состоянии Zj без учета длительности нахождения в каждом состоянии.
Предельные вероятности для системы на рис. 7 могут быть получены путем решения системы [19]:
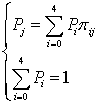 . (19)
. (19)
Для синхронной версии МДПН время пребывания канала в незанятом состоянии, выраженное в количестве тактов, имеет геометрическое распределение с математическим ожиданием:
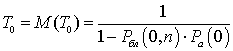 ,
,
при этом прослушивание канала абонентом занимает один тактовый интервал τ:
T1 = τ =1.
Длительность пакетов в процессе функционирования системы связи не изменяется, соответственно время пребывания в состояниях Z2, Z3, Z4 равно длительности передачи пакета, выраженное в количестве тактов:
T2 = T3 = T4 = τm.
Определим переходные вероятности для цепи на рис. 7:
- для Z0 → Z1. Так как после освобождения канала абонент всегда прослушивает канал то:
π01 = 1;
- для Z1 → Z2. Передача абонента завершится успешно, если нет передач от других абонентов, и помеха не исказит пакет:
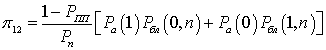 ;
;
- для Z1 → Z3. Данный переход определяется вероятностью искажения пакета помехой:
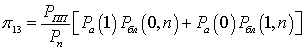 ;
;
- для Z1 → Z4. Будет определяться вероятностью коллизии, в случае если попытку передачи осуществляют более одного абонента:
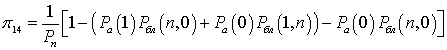 ;
;
- для Zj → Z0. Так как переход в незанятое состояние по завершение цикла передачи осуществляется всегда, то:
π20 = π30 = π40 = 1.
Решая систему (19) и подставляя результаты в (18), получим вероятность нахождения канала в режиме успешной передачи PZ 2, которая будет определять относительную пропускную способность сети с методом доступа МДПН нормированную к единице:
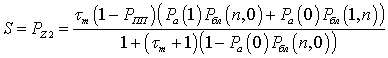 .
.
Данное выражение возможно упростить, при допущении о большом количестве равномерно «слабых» абонентов в сети n→∞:
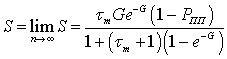 ,
,
где G = λ1+nPповт - интенсивность трафика поступающего в канал связи.
Таким образом, возможно подавление сетей случайного множественного доступа на основе протоколов ALOHA и CSMA/CD которое может быть осуществлено низкоэнергоемкими средствами РЭП за счет использования внутренних особенностей их функционирования. Указанный способ может быть применен к ПРС на основе протоколов IEEE 802.3, IEEE 802.11, а так же ко всем разновидностям доступа к каналу.
Литература
1. Захаренко Г. И., Сапожников В. В., Сапожников В. И., Федосеев В. Е., Савченко К. Ю. Системы связи: уч. пособие. - Ставрополь, изд. СВВАИУ, 2007. – 228 с.
2. Хант Г. Реализация систем для ведения «сетецентрических» (net-centric) войн // МКА: мир ВКТ. 2007. № 7. - с. 64-70.
3. Макаренко С. И., Демчук Д. В. Перспективы использования сетецентрических технологий управления боевыми действиями // Мат. НТК: Перспективы развития средств и комплексов связи. Ч. 3. изд. ВАС (фил. г. Новочеркасск) – Новочеркасск, 2011. – с. 137-142.
4. Макаренко С. И. Проблемы внедрения сетецентрических технологий в Вооруженных силах РФ // Мат. НТК: Перспективы развития средств и комплексов связи. Ч. 2. изд. ВАС (фил. г. Новочеркасск) – Новочеркасск, 2011. – с. 6-14.
5. Владимиров В. И. Информационные основы радиоподавления линий радиосвязи в динамике радиоэлектронного конфликта. Воронеж: ВИРЭ. 2003. – 276 с.
6. Пространственные и вероятностно-временные характеристики эффективности станций ответных помех при подавлении систем радиосвязи. Под ред. В. И. Борисова – Воронеж, ОАО «Концерн «Созвездие», 2007. – 354 с.
7. Клейнрок Л. Вычислительные системы с очередями. – М.: Мир, 1979. – 600 с.
8. Бертсекас Д., Галлагер Р. Сети передачи данных. – М.: Мир, 1989. – 544 с.
9. Бабусенко С. И., Исаев В. В. Статистическое моделирование многопролетных сетей пакетной радиосвязи. – Мат. 18 НТК Техника средств связи – Воронеж, НИИС, 1992.
10. Бабусенко С. И., Исаев В. В. Аналитическая модель маршрутизации в пакетной радиосети. – Мат. 18 НТК Техника средств связи – Воронеж, НИИС, 1992.
11. Courtois P. J., Scheys G., Semal P. Channel-access protocols and routing strategies for mobile packet radio networks. – Philips Journal of Reseach, 1988, vol. 43, № 3/4.
12. Зайдлер Е. Системы передачи дискретной информации. – М.: Связь, 1977. – 512 с.
13. Carlear A. B., Helman. Bistable behavior of ALOHA type systems. - IEEE Trans. Commun. 1975, vol. 23.
14. Yoshikuni Onozato, Scoichi Noguchi. On the thrashing cusp in slotted ALOHA systems. – IEEE Trans. Commun. 1985, vol. 33.
15. Хомячков И. И. Анализ характеристик CSMA/CD сети с конечным числом станций. – Автоматика и выч. техника, 1990. № 1.
16. Присяжнюк С. П., Комашинский В. И. Пакетная радиосвязь // Информация и космос: спец. выпуск. 2009, № 5.
17. Тихонов В. И., Миронов М. А. Марковские процессы. – М.: Сов. радио, 1977. – 485 с.
18. Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1975. – 432 с.
19. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. – М.: Наука, 1987. – 336 с.
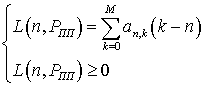 , (1)
, (1)