УДК 3621.385
Исследование
различных способов настройки многоканальных однозазорных резонаторов на
кратные резонансные частоты
В. А. Сенчуров, В. А. Царев
Саратовский государственный технический университет, кафедра «Электронные приборы и устройства»
Получена 8 сентября 2011 г.
Аннотация. Приведены результаты расчета по двухмерным и трехмерной программам клистронных многоканальных однозазорных резонаторов разной формы, настроенных на кратные частоты, соответствующие основному и первому высшему видам колебаний. Найдена оптимальная форма резонаторов, соответствующая максимуму отношения эффективного характеристического сопротивления на единицу длины резонатора.
Ключевые слова: многоканальные однозазорные резонаторы, клистронные однозазорные резонаторы, многолучевой клистрон.
Abstract. Calculation results are conducted on two-dimensional and three-dimensional programs for the klystron multi-channel one-gap resonators of different forms, each with multiple frequencies, corresponding to the main and first higher types of oscillations. An optimal form of resonators is found, corresponding to the maximum of the relationship of effective characteristic resistance per unit length of the resonator.
Keywords: multi-channel one-gap resonators, klystron one-gap resonators, multibeam klystron.
В настоящее время в радиоэлектронике ведется активная разработка электровакуумных СВЧ-приборов клистронного типа [1], предназначенных для получения СВЧ-мощности на двух кратных частотах. Данный тип приборов может быть использован в радиолокации, радиопротиводействии и в других областях техники. Одним из основных требований, предъявляемым к мощным усилительным клистронам является получение высокого КПД~70-80%. Высокий КПД таких приборов достигается за счет несинусоидальной скоростной модуляции, которая реализуется при введении в конструкцию многорезонаторной системы двух дополнительных однозазорных резонаторов, имеющих собственные частоты, равные удвоенной частоте основного сигнала. Это увеличивает габариты и массу такого устройства. Устранить этот недостаток можно за счет применения вместо двух резонаторов одного однозазорного резонатора, настроенного на две кратные резонансные частоты.
Однако для многолучевых конструкций приборов СВЧ такие резонаторы пока не исследовались и не применялись. Поэтому основной задачей настоящей работы является поиск оптимальной формы и размеров однозазорных резонаторов при работе на основном и первом высшем виде колебаний с кратными резонансными частотами, а также оценка эффективности применения этих систем в многолучевых приборах.
В работе [2] описана методика синтеза ступенчато-неоднородного коаксиального однозазорного резонатора, настраиваемого на основную частоту и ее вторую гармонику. Конструкция такого резонатора показана на рис. 1. Эта методика положена в основу программы синтеза многолучевых резонаторов с кратными резонансными частотами [3].
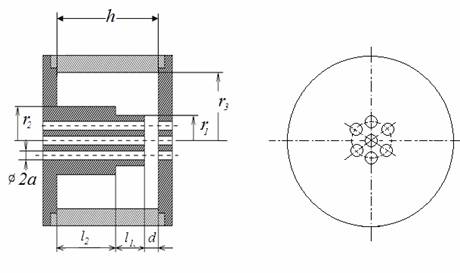
Рис. 1. Конструкция многоканального резонатора клистрона.
С помощью этой программы можно найти оптимальные
соотношения основных геометрических размеров, определяющих резонанс
одновременно на двух частотах 
и 
, соответствующих основной и первой высшей
моде электромагнитных колебаний. Для решения задачи синтеза использовался
метод эквивалентной схемы с полураспределенными параметрами [4], согласно которому резонатор можно было представить
в виде эквивалентной ступенчато-неоднородной длинной линии, образованной
отрезками 
и 
с
волновыми сопротивлениями 
и 
. Эта линия замкнута на одном конце, а на
другом конце она нагружена на емкость зазора С0 (рис.2). Емкость
скачка волнового сопротивления представлена на схеме емкостью 
.
Рис.2 Эквивалентная схема резонатора.
Входная проводимость короткозамкнутого отрезка линии в сечении 2-2
,
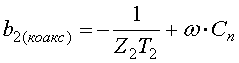(1)
где 
В
сечении 1-1 входную проводимость отрезка линии, нагруженной на реактивную
проводимость 
, можно рассчитать с помощью уравнения:
, (2)
где 
.
Условие резонанса для такой линии может быть записано как сумма реактивных проводимостей в сечении 1-1.
= 
=0.
(3)
Суммарная нормированная проводимость в сечении 1-1 может быть записана в виде
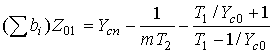=0.
(4)
Используя метод подобия, с помощью уравнения (4) можно перейти от коаксиальной формы конструкции резонатора к другим геометрическим формам, отличающихся уменьшенными продольными размерами.
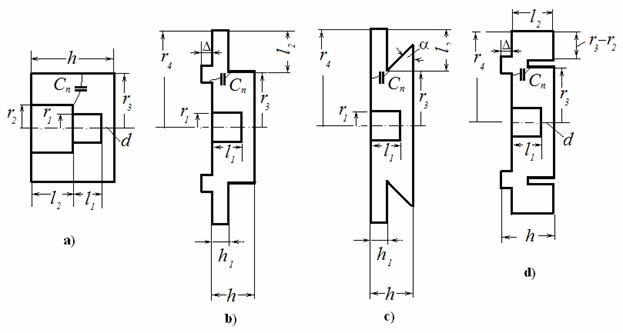
Рис. 3. Четыре типа конструкции многолучевых однозазорных резонаторов.
В
резонаторе на рис. 3b участок l1, такой же,
как и в коаксиальном резонаторе- прототипе на рис. 3а. Коаксиальный участок l2
заменен на короткозамкнутый отрезок радиальной линии, имеющей такую же
проводимость 
, как и в коаксиальной линии.
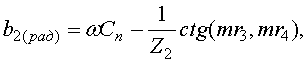(5)
где 
-
волновое число, 
- емкостная проводимость скачка
волнового сопротивления,
-
входное волновое сопротивление радиальной линии, имеющей внутренний радиус 
, внешний радиус 
и
высоту h,
-
малый радиальный котангенс, определяемый из уравнения:
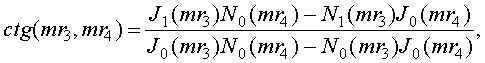(6)
где 
- соответствующие функции Бесселя и
Неймана нулевого и первого порядка.
Условия подобия резонаторов можно записать в следующем виде:
=
, 
=
.
(7)
При
выполнении этих условий резонаторы будут иметь одинаковые резонансные частоты. Для
того чтобы обеспечить равенство емкостей =
в конструкции резонатора, показанного на
рис. 3b, предусмотрены пазы в стенке
резонатора. Изменяя глубину паза, можно изменять емкость . В конструкции, показанной на рис. 3с,
подбор величины емкости может быть осуществлен путем изменения угла 
. Конструкция резонатора, показанная на
рис. 3 d, имеет вид свернутой
коаксиальной линии. Место стыка линий с разными волновыми сопротивлениями
представляет собой кольцевой выступ, емкость которого также можно регулировать изменением
глубины паза, расположенного на другой стенке резонатора.
Для подтверждения возможности создания резонаторов, показанных на рис. 3, были проведены численные расчеты с помощью программ «BEZONE» [3], «AZIMUTH»[5], «HFSS»[6].
Ниже приведены результаты, полученные с помощью программы «AZIMUTH» для резонаторов 3а, 3с, 3d, настроенных на 2 кратные частоты: 2450 МГц и 4900 МГц. На рис. 4 показано распределение электрического поля для основного и первого высшего вида колебаний резонатора 3а. Так как программа двухмерная, то отверстия в пролетной трубе не моделировались, то есть рассматривался плоский зазор.
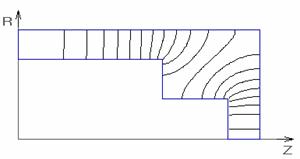
Рис.4. Картина распределения полей для основного и первого высшего видов колебаний резонатора 3а.
Характеристическое
сопротивление для резонатора, показанного на рис. 3а, при R=0 на
основном виде колебаний 
=51.2 Ом, на первом
высшем виде колебаний =21.9 Ом. Геометрические размеры
резонатора: 
=6.95 мм, 
=13.78
мм, 
=18.89 мм, 
=8.66
мм, 
=19.14 мм, d=4.23
мм, а=1.73 мм.
Рис.5. Картина распределения полей для основного и первого высшего видов колебаний резонатора 3с.
Характеристическое
сопротивление для резонатора, показанного на рисунке 3с при R=0 на
основном виде колебаний =51.9 Ом, на первом
высшем виде колебаний =5.8 Ом. Геометрические размеры
резонатора с углом следующие: =8.83 мм, =23.61 мм, 
=39.3
мм, =9.24 мм, h=13.14
мм, d=3.9 мм, а=2.05 мм.
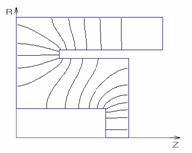
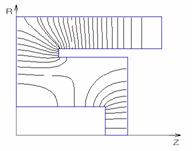
Рис.6. Картина распределения полей для основного и первого высшего видов колебаний резонатора типа 3d).
Характеристическое сопротивление
для резонатора, показанного на рисунке 3d,
при
R=0 на основном виде колебаний =60.47 Ом, на первом высшем виде колебаний
=19.9 Ом. Геометрические размеры
резонатора: =5.22 мм, =14.2
мм, =21.52 мм, h=20.4
мм, =12.51 мм, d=3.18
мм, a=1.15 мм.
Был проведен сравнительный анализ эффективности взаимодействия 3-х типов резонаторов с электронным пучком для основного (f1=2450 МГц) и первого высшего вида колебаний (f2=4900 МГц) по критерию [7]:
,
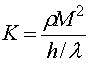(8)
где -
характеристическое сопротивление,
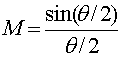– коэффициент
эффективности взаимодействия,
где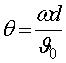 
- невозмущенный
угол пролета электронов через зазор резонатора d со
скоростью 
h – продольная длина резонаторов,
-
длина волны.
Скорость электронов 
рассчитывалась
из закона сохранения энергии при ускоряющем напряжении 
=10кВ,
соответствующем невозмущенному углу пролета 
1.
Результаты расчета критерия эффективности 3-х исследованных типов резонаторов приведены в таблице 1.
Таблица 1.
|
№ резонатора |
|
|
|
3а |
177.1 |
55.1 |
|
3c |
445 |
38 |
|
3d |
347.7 |
94.7 |
и 
-
критерии эффективности для основного и первого высшего видов колебаний
соответственно. Видно, что наибольшее характеристическое сопротивление на
единицу длины резонатора при взаимодействии электронного пучка с
электромагнитным полем в резонаторе на основном виде колебаний достигается в резонаторе
3с, но при этом у него худшее взаимодействие на первом высшем виде колебаний.
Наиболее оптимальным для использования на двух кратных частотах является резонатор
3d, поскольку у него больший критерий эффективности взаимодействия на первом
высшем виде колебаний, чем у остальных типов резонаторов.
Исследована
возможность подстройки резонатора 3с на кратные частоты за счет изменения
подстроечного угла
(см. рис. 3с). Для оценки
погрешности, связанной с не учетом провисания поля в пролетных каналах при
расчетах по программе «AZIMUTH», проводился
также расчет по трехмерной программе «HFSS».
Результаты расчетов приведены в таблица 2.
Таблица 2. Сравнение результатов расчета резонатора 3с в программе «HFSS» и программе «AZIMUTH».
|
|
|
|
|
|
|
|
|
0 |
2426 |
2529 |
4883 |
5014 |
4.24 |
2.68 |
|
7.11 |
2461 |
2516 |
4907 |
5013 |
2.23 |
2.16 |
|
14.01 |
2454 |
2503 |
4901 |
5006 |
1.99 |
2.14 |
|
20.53 |
2443 |
2491 |
4886 |
5002 |
1.96 |
2.37 |
|
26.54 |
2431 |
2479 |
4877 |
4998 |
1.94 |
2.42 |
|
31.97 |
2434 |
2466 |
4882 |
4994 |
0.9 |
2.36 |
, ° - подстроечный
угол,
, 
- основной и первый высший тип колебаний,
рассчитанный в программе «HFSS»,
, 
- основной и первый высший тип колебаний,
рассчитанный в программе «AZIMUTH».
, 
- погрешность между результатами расчета двух
программ для основного и первого высшего типа колебаний, соответственно.
Из
таблицы 2 следует, что наибольшая погрешность расчетов частоты основного вида
колебаний (около 4%) наблюдается при малых углах . При
углах пролета больше 30° погрешность пренебрежимо мала. На первом высшем виде
колебаний погрешность составляет примерно 2%.
Установлено,
что за счет оптимального выбора подстроечного угла можно
настроить резонатор на кратные частоты.
На рис.
7 показан график зависимости и /2 от подстроечного угла . Точки, где две кривые пересекаются,
соответствуют достижению кратности частот в резонаторе.
График зависимости основного и первого высшего видов колебаний от изменения угла в резонаторе.
Рис. 7. График зависимости и /2 от подстроечного угла .
В
резонаторе 3d подстройка кратности частот была проведена за счет изменения
подстроечного паза 
. Результаты расчета приведены в
таблице 3.
Таблица 3.
|
|
|
|
|
3 |
2393 |
4856 |
|
2 |
2421 |
4874 |
|
1 |
2442 |
4897 |
|
0 |
2451.7 |
4896 |
На
рис. 8 показан график зависимости 
, 
/2 от длины подстроечного паза . Точка, где две кривые пересекаются,
соответствуют достижению кратности частот в резонаторе.
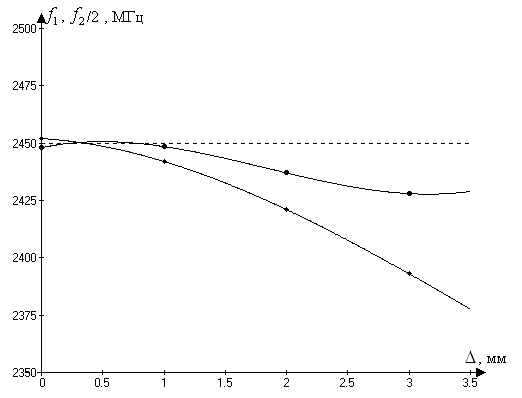
Рис. 8.
График зависимости , /2 от
длины подстроечного паза .
Заключение
Найдена оптимальная форма резонаторов, соответствующая максимуму отношения эффективного характеристического сопротивления на единицу длины резонатора.
Дана оценка погрешности расчета резонансной частоты основного и первого высшего видов колебаний по двухмерным и трехмерной программам.
Исследованы различные формы подстройки резонаторов на кратные частоты.
Применение таких резонаторов позволит существенно уменьшить массогабаритные параметры высокоэффективных многолучевых клистронов.
Литература
[1] Королев А. Н., Лямзин В. М., Мамонтов А. В., Симонов К. Г. СВЧ-прибор клистронного типа (варианты). Патент на полезную модель № 2390870, г. Фрязино, 2010.
[2] Синтез однозазорных резонаторов с кратными резонансными частотами для многолучевых СВЧ приборов клистронного типа/ Царев В.А., Сенчуров В.А. // Материалы Всероссийской науч.-практ. конф., Саратов, 2009, с. 247.-249.
[3] Царев В.А., Сенчуров В.А. «BEZONE» // Свидетельство об официальной регистрации программы для ЭВМ №2011613602 от 10.05.2011.
[4] Орлов С.И. Расчет и конструирование коаксиальных резонаторов, Изд-во "Советское Радио", 1970, 256 с
[5] Гpигоpьев А.Д., Силаев С.А. Расчет электpомагнитного поля азимутально неодноpодных типов колебаний аксиально-симметpичных pезонатоpов с пpоизвольной
фоpмой обpазующей. Электpонная техника. Сеp.1, Электpоника СВЧ, 1981, вып. 2, стp. 62 -65.
[6] Ansoft HFSS. Corpo., Pittsburgh, PA, USA, 1999.
[7] Царев В.А., Мирошниченко А.Ю., Смирнов С.В. Нелинейный критерий подобия тороидальных резонаторов // СВЧ-техника и телекоммуникационные технологии: материалы XIX междунар. Крымской конф., 14-18 сент. 2009 г., Севастополь, Крым, Украина. - Севастополь, 2009. - С. 139-140.