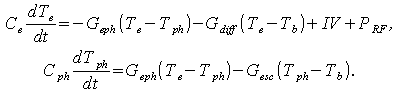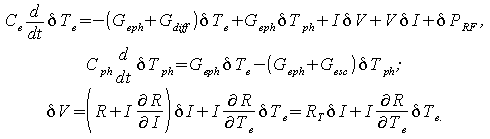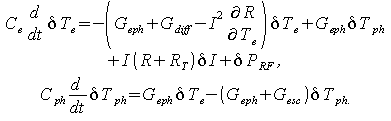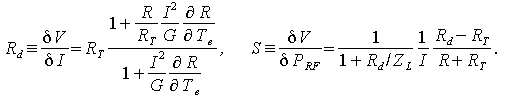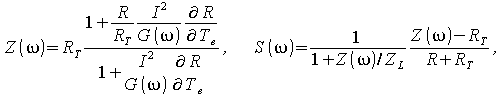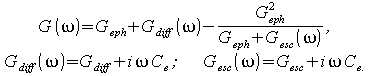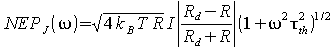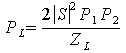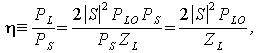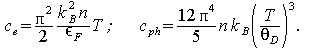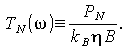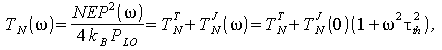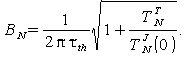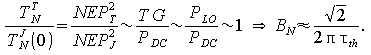вольт-ваттная чувствительность и шумовая температура детектора на эффекте электронного разогрева в ультратонких сверхпроводниковых пленках

 

C. А. Рябчун, И. В. Третьяков, И. В. Пентин,  М. И. Финкель,
П. А. Ларионов, А. В. Масленникова

Московский педагогический государственный университет

 

Получена 5 сентября 2012 г.

 

Аннотация.  В статье приведены основные аспекты явления электронного разогрева в сверхпроводниковых пленках применительно к детекторам электромагнитного излучения на основе этого явления. В рамках линеаризованных уравнений теплового баланса для электрон-фононной системы пленки получены аналитические выражения для вольт-ваттной чувствительности и шумовой температуры детектора.

Ключевые слова: эффект электронного разогрева в сверхпроводниках, детекторы электромагнитного излучения.

Abstract: The paper presents the main aspects of the hot-electron effect in superconducting films, focusing on the applications of this effect in detectors of electromagnetic radiation. Within the framework of linearised heat balance equations analytic expressions have been obtained for the voltage responsivity and  noise temperature of such hot-electron detectors.

Keywords: hot-electron effect in superconductors, detectors of electromagnetic radiation.

 

Введение

Ряд процессов, происходящих в межзвездном пространстве, в Млечном Пути и других галактиках, имеют характерные линии испускания и поглощения, лежащие в  области частот примерно 0.3 – 3 ТГц (0.1 – 1 мм), называемой терагерцовым диапазоном [1-2].  Такие соединения, как CO, CS, SO, SO₂, HCO⁺, HCN, C, N⁺ и C⁺, могут наблюдаться в этой части спектра электромагнитного излучения. Рождение звезды происходит в результате гравитационного коллапса межзвездных пылевых туманностей. В процессе коллапса основная часть энергии туманности переходит в электромагнитное излучение терагерцового диапазона. Регистрация этого излучения с помощью приемников терагерцового диапазона и анализ полученных данных дают богатую информацию о плотности, температуре и других характеристиках  этих туманностей, что необходимо для дальнейшего изучения эволюции звезд и планетных формирований. Таким образом, наблюдения, проведенные в терагерцовой области, могут способствовать лучшему пониманию явлений, протекающих в гигантских межзвездных молекулярных облаках и областях формирования звезд, а также дать информацию о различных процессах, протекающих в Млечном Пути и других галактиках.

2. Супергетеродинные приемники

Проведение наблюдений в терагерцовой области спектра осложнятеся сильным поглощением электромагнитного излучения этого диапазона в земной атмосфере, главным образом, молекулами O₂, CO₂ и H₂O. Это приводит к необходимости располагать телескопы в высокогорных областях на высоте порядка 5000 м над уровнем моря, где прозрачность атмосферы выше (RLT [1], SMA [3], ALMA [4]) или базировать на самолетах (SOFIA [5]), или же запускать в космос (Herschel [6]).

Приемники электромагнитного излучения можно разделить на два класса: супергетеродинные и прямого детектирования. При супергетеродинном  приеме сохраняется фаза принимаемого сигнала, при прямом детектировании вся информация о фазе принимаемого сигнала теряется. К приемникам прямого детектирования приемникам относятся болометры и счетчики фотонов.

Основными параметрами супергетеродинных приемников являются шумовая температура и полоса преобразования. В настоящее время на частотах ниже 1 ТГц безусловными лидерами являются смесители на туннельном переходе свехпроводник-изолятор-сверхпроводник (СИС смесители)  из-за их низкой шумовой температуры (несколько hν/k_B) и стабильности по отношению к флуктуациям мощности гетеродина в время работы. Поэтому они широко используются в радиотелескопах таких как SMA и ALMA, работающих в этом диапазоне. К сожалению, шумовая температура СИС смесителя резко возрастает, когда частота излучения приближается или превышает величину энергетической щели сверхпроводящего материала, из которого он изготовлен [7]. На частотах выше 1 ТГц предпочтение отдается смесителям на эффекте разогрева электронов в сверхпроводниках (hot-electron bolometer (HEB) mixer) [8]. Эти смесители были выбраны для терагерцовой астрономии из-за того, что они не имеют частотных ограничений по механизму смешения [9], обладают низкой шумовой температурой (менее 1K/ГГц), и широкой полосой преобразования [10], и также, поскольку они требуют меньше мощности гереродина, чем смесители на диодах Шоттки. Поэтому в супергетеродинном приемнике для дальней ИК области (Heterodyne Instrument for the Far-Infrared - HIFI), который был запущен в 2009 г. на борту космической обсерватории Herschel HEB смеситель используется для полосы частот 1410-1910 ГГц. Два супергетеродинных приемника, CASIMIR и GREAT, на основе HEB смесителей, работающих в частотных диапазонах 1.2-2.1 ТГц  и 1.5-5 ТГц, будут запущены на борту самолетной обсерватории SOFIA. HEB смеситель будет использован для наблюдений на частоте 1.8 ТГц в проекте воздушного базирования TELIS [11]. Наземный телескоп APEX, расположенный в Северном Чили (Llano de Chajnantor) на высоте 5105 м над уровнем моря использует HEB смеситель для покрытия частотного диапазона 1250-1384 ГГц [12]. Receiver Lab Telescope, построенный в Гарвард-Смитсониевском астрофизическом центре в настоящее время один из немногих наземных телескопов, работающих на частотах 0.8-1.5 ТГц. [13]. Проект Миллиметрон [14], разрабатываемый Астрокосмическим Центром ФИАН им. П. Н. Лебедева, будет использовать HEB приемники для проведения наблюдений на частотах выше 1 ТГц.

3. Смесители на эффекте электронного разогрева в сверхпроводниках

Эффект электронного разогрева реализуется в тонких пленках нормальных и сверхпроводящих материалов при условии малости времени ухода фононов из пленки в подложку по сравнению со временем релаксации фононов за счет рассеяния на электронах и куперовских парах (в случае сверхпроводника). В этом случае поглощение пленкой электромагнитного излучения не приводит к её нагреву как целого, а лишь к нагреву электронной подсистемы, которая при этом описывается функцией распределения Ферми с температурой, отличной от температуры фононов [15-17]. Если время электрон-фононного взаимодействия велико по сравнению с временем диффузии электронов из пленки, то релаксация электронной подсистемы будет осуществляться за счет диффузии. В этом случае говорят о диффузионном охлаждении электронной подсистемы [18]. Если же неравновесные электроны не успевают диффундировать из пленки, а рассеиваются на фононах, то реализуется фононный механизм охлаждения электронов [19]. Поскольку время диффузии пропорционально квадрату линейных размеров пленки, то какой тип охлаждения будет доминировать, определяется геометрией пленки. Однако диффузия электронов возможна лишь в том случае, если материал контактов нормальный, иначе электроны будут андреевски отражены [20].

Сверхпроводниковый болометр на эффекте электронного разогрева представляет собой полоску сверхпроводника толщиной в несколько нанометров, включенную между терминалами планарной антенны. Необходимость антенны связана с тем, что в терагерцовом диапазоне длина волны порядка 0.1 мм, в то время как характерные размеры болометра порядка 1 мкм. В зависимости от приложений антенна может быть логоспиральной, двухщелевой или дипольной. Электромагнитная волна, падая на антенну, наводит в ней высокочастотные токи, которые при протекании через болометр приводят к повышению его температуры. Особенностью сверхпроводящих болометров является то, что зависимость их сопротивления от температуры в близи сверхпроводящего перехода очень резкая, вследствие чего достаточно незначительного повышения температуры болометра, чтобы его сопротивление существенно выросло. При протекании тока через болометр это повышение сопротивления приводит к возникновению напряжения на нем, которое можно зарегестрировать.Существует две основные модели, описывающие динамику сверхпроводящей полоски, поглощающую электромагнитное излучение: модель однородного разогрева и модель горячего пятна [21]. В модели однородного разогрева предполагается что вся пленка под действием излучения и транспортного тока переведена в резистивное состояние. Формально такая ситуация описывается системой нелинейных уравнений теплового баланса, допускающих лишь численное решение при заданных граничных и начальных условиях [22]. Упрощения можно достичь, если провести линеаризацию уравнений, считая, что состояние пленки близко к равновесному [23, 24]. В модели горячего пятна предполагается, что есть некоторая область пленки (домен), в которой сверхпроводимость разрушена [25, 26]. Размер нормального домена определяется транспортным током и поглощенной мощностью. Уравнения теплового баланса записываются отдельно для нормальной и сверхпроводящей областей. Соответствующие решения «сшиваются» на границе номральной и сверхпроводящей фаз на основании требования непрерывности решения.

Важными параметрами любого болометра являются его вольт-ваттная (или ампер-ватная) чувствительность и эквивалентная мощность шума (по-английски –  noise equivalent power, NEP). Эквивалентная мощность шума определяется как мощность излучения, падающего на болометра, при которой отношение сигнал-шум равно единице [13]. Основными источниками шума в болометре являются термодинамические флуктуации температуры, шум Джонсона и фотонный щум (в области Релея-Джинса) [28, 29]. Фундаментальным ограничением являются термодинамические флуктуации температуры, которые напрямую зависят от температуры рассматриваемой системы и ее связи с термостатом, поэтому для уменьшения соответствующей эквивалентной мощности шума необходимо понижать температуру и уменьшать коэффициент теплоотвода между системой и термостатом.

В модели однородного электронного разогрева предполагается, что температуры электронной и фононной подсистем сверхпроводящей пленки не зависят от координат. Данное предположение может быть справедливо лишь приближенно вследствие того, что электронная температура на границе между пленкой и массивными контактами  равна температуре контактов. Поэтому физически более правильной,  является модель неоднородного разогрева, учитывающая пространственное изменение температуры.

Линеаризованные уравнения теплового баланса для электронной и фононной подсистем сверхпроводящей пленки, находящейся в контакте с тепловым резервуаром (подложкой) при температуре T_b, могут быть записаны следующим образом:

	(1)

Здесь c_e и c_ph – удельные теплоемкости электронной и фононной подсистем соответственно; T_e и T_ph – температуры электронной и фононной подсистем соответственно; G_eph, G_diff и G_esc – феноменологические коэффициенты теплоотвода, связанные сответственно с электрон-фононным взаимодействием, диффузией электронов в контакты и уходом неравновесных фононов в подложку; I и V – ток в пленке и напряжение на ней; P_RF – мощность падающего излучения.

Система уравнений (1) должна быть еще дополнена уравнением, связывающем ток и напряжение:

	(2)

где подчеркнуто, что в общем случае сопротивление определяется не только электронной температурой, но и транспортным током. Зависимость сопротивления от тока проявляется в возникновении вихрей и центров проскальзывания фазы.

         Варьирование уравнений (1) и (2) дает

	(3)

Величина называется термическим сопротивлением болометра и, как будет показано ниже, равна его импедансу на частотах высоких по сравнению с постоянной времени болометра. Исключение из уравнений (3) дает

	(4)

 В стационарном режиме, когда внешние параметры остаются постоянными, а, значит, производные по времени в уравнениях теплового баланса обращаются в нуль,  из уравнений (4) получаем выражения для дифференциального сопротивления болометра и его вольт-ваттной чувствительности:

	(5)

 При этом введены следующие параметры: 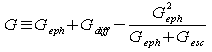 – эффективный коэффициент теплоотвода; Z_L – сопротивление нагрузочного сопротивления, с которого производится непосредственный съем сигнального напряжения с болометра.

Наиболее интересным с практической точки зрения представляется случай, когда ток и напряжение, а также мощность падающего излучения меняются по гармоническому закону , поскольку остальные нестационарные случаи сводятся к нему посредством преобразования Фурье вследствие линейности уравнений теплового баланса. Формальная замена производных по времени приводит дифференциальные уравнения (4) к алгебраическим, что позволяет сразу написать выражения для импеданса болометра и частотной зависимости его вольт-ваттной чувствительности:

	(6)

где введены обозначения:

	(7)

         Как было сказано выше, параметром, характеризующим шумы болометра, является эквивалентная мощность шума (NEP). Можно показать, что эквивалентные мощности шума термодинамических флуктуаций и шума Джонсона равны, соответственно [28, 29]

	(8)
	(9)

где I – транспотрный ток, τ_th – время релаксации электронной температуры. Полная эквалентная мощность шума равна

	(10)

 Болометр может работать как смеситель благодаря тому факту, что изменение его температуры пропорционально поглощенной мощности, поэтому, если на болометр падают две электромагнитные волны, то мгновенная мощность усредненная по его постоянной времени равна

	(11)

Здесь A_b – площадь болометра, E₁ и E₂ – напряженности электрических полей волн 1 и 2, P₁ и P₂ – соответствующие усредненные мощности. При этом предполагается, что частоты ω₁ и  ω₂ велики по сравнению с обратным временем релаксации температуры болометра, а модуль их разности ω_IF = |ω₁ – ω₂|, именуемый промежуточной частотой, мал по сравнению с обратным временем релаксации.

Переменное напряжение, возникающее на смесителе при поглощении излучения

	(12)

где в последнем равенстве учтено соотношение между сопротивлением на смесителе и нагрузочном сопротивлении. Тогда средняя мощность, выделившееся на этом сопротивлении равна

	(13)

Когда болометр является частью приемника, например, радиотелескопа, источники 1 и 2 суть гетеродин (local oscillator, LO) и принимаемый сигнал (S). В этом случае можно ввести понятие коэффициента преобразования смесителя, определяемого как отношение мощности, выделившейся в нагрузке к мощности принимаемого сигнала:

	(14)

где P_LO – мощность гетеродина,  P_S – мощность принимаемого сигнала.

Феноменологические коэффициенты теплоотвода можно выразить через соответствующие времена релаксации и теплоемкости (приводимые ниже выражения, по существу, являются определениями коэффициентов теплоотвода):

	(15)

Характерные времена можно определить из экспериментральной зависимости коэффициента преобразования смесителя от промежуточной частоты, куда эти времена войдут как подгоночные параметры. Время ухода неравновесных фононов в подложку пропорционально толщине пленки:

	(16)

где d – толщина пленки, u – скорость звука, и α – акустическая прозрачность границы пленка-подложка. Зависимости электронной и фононной удельных теплоемкостей от температуры даются в рамках моделей Зоммерфельда и Дебая соответственно [30]:

	(17)

Здесь n – концентрация электронов, ε_F – энергия Ферми, Θ_D – температура Дебая.

         Для характеристики шумов когерентного приемника вводится понятие шумовой температуры, приведенной ко входу. Если P_N – мощность шумов на выходе приемника с коэффициентом преобразования η, измеренная в полосе B, то шумовая температура определяется как

	(18)

С другой стороны, мощность шумов на выходе приемника можно записать как

	(19)

Собирая вместе выражения (8)-(10), (18), (19), получаем для шумовой температуры

	(20)

откуда видно, что присутствие шума Джонсона приводит к монотонному возрастанию шумовой температуры с частотой. Это позволяет ввести понятие верхней границы шумовой полосы, как частоты, при которой значение шумовой температуры увеличивается в два раза по сравнению со значением на частотах, удовлетворяющих неравентству ωτ_th << 1:

	(21)

Оценим величину квадратного корня в (21):

	(22)

Таким образом, присутствие шума, обусловленного термодинамическими флуктуациями температуры, приводит к тому, что шумовая полоса примерно в полтора раза превышает полосу преобразования (величину 1/2πτ_th).

4. Выводы

Рассмотрены практические аспекты эффекта электронного разогрева в сверхпроводниковых пленках. В рамках линеаризованных уравнений модели однородного электронного разогрева получены аналитические выражения для вольт-ваттной чувствительности и шумовой температуры сверхпроводникового болометра, которые  могут быть использованы для анализа экспериментальных результатов.

Работа выполнена в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг., государственный контракт № 16.740.11.0580 от 30 мая 2011 г., а также при поддержке гранта Президента Российской Федерации, договор № 16.120.11.4005-МК от 01.02.2012.

 

Литература

1.     Prospects for terahertz radio astronomy from northern Chile / R. Blundell, J. W. Barrett, H. Gibson, C. Gottleib, T. R. Hunter, R. Kimberk, S. Leiker, D. Marrone, D. Meledin, S. Paine, D. C. Papa, R. G. Plante, P. Riddle, M. J. Smith, T. K. Sridharan, C.-Y. E. Tong, R. W. Wilson, M. Diaz, L. Bronfman, J. May, A. Otarola, S. J. E. Radford // Proceedings of the 13th International Symposium on Space Terahertz Technology / Harvard University – Cambridge, MA, USA: 2002. – p. 159.

2.     Ground-based terahertz CO spectroscopy towards Orion / J. Kawamura, T.R. Hunter, C.Y.E. Tong, R. Blundell, D.C. Papa, F. Patt, W. Peters, T.L. Wilson, C. Henkel, G. Gol'tsman, and E. Gershenzon // Astron. Astrophys. – 2002. – vol. 394. – pp. 271-274.

3.     SMA - Submillimeter Array. // [Электронный ресурс]. URL: http://www.cfa.harvard.edu/sma/

4.     ALMA - Atacama  Large Millimeter Array. // [Электронный ресурс]. URL: http://www.almaobservatory.org/

5.     SOFIA - Stratospheric Observatory for Infrared Astronomy. // [Электронный ресурс]. URL: http://www.sofia.usra.edu/.

6.     Hot-electron bolometer terahertz mixers for the Herschel Space Observatory / S. Cherednichenko, V. Drakinskiy, T. Berg, P. Khosropanah, and E. Kollberg // Review of Scientific Instruments. – 2008. – 79. – 034501.

7.     John R. Tucker, Marc J. Feldman. Quantum detection at millimeter wavelengths // Rev. Mod. Phys. – 1985. – vol. 57. – p. 1055.

8.     Смеситель миллиметрового и субмиллиметрового диапазонов волн на основе разогрева электронов в резистивном состоянии сверхпроводниковых пленок / М. Гершензон, Г. Н. Гольцман, И. Г. Гогидзе, Ю. П. Гусев, А. И. Елантьев, Б. С. Карасик, А. М. Люлькин, А. Д. Семенов // СФХТ. – 1990. – том 3, часть I. – стр. 2143-2160.

9.     Intense Electromagnetic Radiation Heating of Electrons of a Superconductor in the Resistive State / E. M. Gershenzon, G. N. Gol’tsman, A. I. Elant’ev, B. S. Karasik, and S. E. Potoskuev // Sov. J. Temp. Phys. – 1988. – vol. 14, no. 7. – pp. 414-420.

10.                                                           Low noise and wide bandwidth of NbN hot-electron bolometer mixers / I.  Tretyakov, S. Ryabchun, M. Finkel, A. Maslennikova, N. Kaurova, A. Lobastova, B. Voronov, and G. Gol’tsman // Applied Physics Letters. – 2011. – 98. – 033507.

11. TELLIS - Terahertz and submillimeter Limb Sounder. – Internet page. – 2012. http://www.sron.nl/index.php?option=com_content&view=article&id=99&Itemid=238.

12.  APEX - Atacama Pathfinder Experiment. // [Электронный ресурс]. URL: http://www.apex-telescope.org/.

13.   Observations in the 1.3 and 1.5 THz Atmospheric Windows with the Receiver Lab Telescope / D. P. Marrone, R. Blundell, E. Tong, S. N. Paine, D. Loudkov, J. H. Kawamura, D. Luhr, C. Barrientos // Proceedings of the 16th International Symposium on Space Terahertz Technology / Goteborg, Sweden: 2005. – p. 64.

14.  W. Wild, N. Kardashev. Millimetron—a large Russian-European submillimeter space observatory // Experimental Astronomy. – 2009. – 23. – pp. 221-244.

15. Разогрев квазичастиц в сверхпроводящей пленке, находящейся в резистивном состоянии / Е. М. Гершензон, М. Е. Гершензон, Г. Н. Гольцман, А. Д. Семенов, А. В. Сергеев // Письма в ЖЭТФ. – 1981. –  том 34, вып. 5. — стр. 281-285.

16. Разогрев электронов в резистивном состоянии сверхпроводника под действием электромагнитного излучения / Е. М. Гершензон, М. Е. Гершензон, Г. Н. Гольцман, А. Д. Семенов, А. В. Сергеев // ЖЭТФ. — 1984. — том. 86, вып. 2. — стр. 758-774.

17.   Неселективное воздействие электромагнитного излучения на сверхпроводящую пленку в резистивном состоянии / Е. М. Гершензон, М. Е. Гершензон, Г. Н. Гольцман, А. Д. Семенов, А. В. Сергеев // Письма в ЖЭТФ. — 1982. – том. 36, вып. 7. — стр. 241-244.

18.   D. Prober. Superconducting terahertz mixer using a transition-edge microbolometer // Appl.Phys.Lett. – 1993. – vol. 62, issue 17. – p. 2119.

19. E. M. Gershenzon et al., Supercond., Phys. Chem. Technol. 3,. 1582 (1990).

20.  M. Tinkham. Introduction to Superconductivity // Dover Publications Inc. –  New York, NY, USA: 2004.

21. Hot-electron effect in superconductors and its applications for radiation sensors / Alexei D Semenov, Gregory N Gol’tsman, and Roman Sobolewski // Supercond. Sci. Technol. – 2002. – vol. 15. – pp. R1–R16.

22. Relaxation between electrons and the crystalline lattice / M. L. Kaganov, I. M. Lifshitz, and L. V. Tanatarov // Sov. Phys. JETP – 1957. – vol. 4. – pp. 173-178.

23.  N. Perrin, C. Vanneste. Response of superconducting films to a perodic optical irradiation // Phys. Rev. B – 1983. – vol. 28. – pp. 5150-5160.

24.   Rigorous analysis of a superconducting hot-electron bolometer mixer: theory and comparison with experiment / R. S. Nebosis, A. D. Semenov, Yu. P. Gousev, and K. F. Renk // Proceedings of the 7th International Symposium on Space Terahertz Technology / University of Virginia. - Charlottesville, VA, USA: 1996. – p. 601-613.

25.  Self-heating hotspots in superconducting thin-film microbridges / W. J. Skocpol, M. R. Beasley, and M. Tinkham // Journal of Applied Physics – 1974. – vol. 45. – pp. 4054-4066.

26. Hotspot mixing: A framework for heterodyne mixing in superconducting hot-electron bolometers / D. Wilms Floet, E. Miedema, T. M. Klapwijk, and J. R. Gao // Applied Physics Letters – 1999. – vol. 74. – pp. 433-435.

27. G. Reike. Detection of light from the unltraviolet to the submillimeter, 2^nd edition // Cambridge University Press. – Cambridge, UK: 2003.

28.    K. Rohlfs, T. L. Wilson, Tools of Radio Astronomy, 4th edition // Springer. – New York, USA: 2000.

29.  R. L. Richards, Bolometers for infrared and millimeter waves // Journal of Applied Physics – 1994. – vol. 76 – pp. 1-24.

30.  N. W. Ashcroft, and N. D. Mermin, Solid State Physics // Saunders. – Philadelphia, USA: 1976.