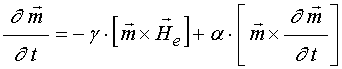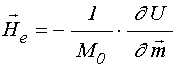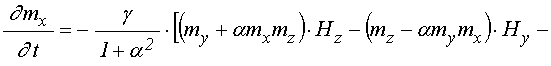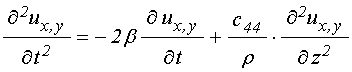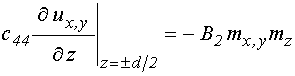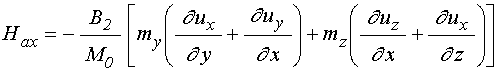"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2015

оглавление

УДК 537.874; 537.624

НЕЛИНЕЙНЫЕ ГИПЕРЗВУКОВЫЕ КОЛЕБАНИЯ МАГНИТОСТРИКЦИОННОГО ПРЕОБРАЗОВАТЕЛЯ НА ЧАСТОТАХ,
КРАТНЫХ ЧАСТОТЕ ВОЗБУЖДЕНИЯ

ЧАСТЬ 1. ДЕЛЕНИЕ ЧАСТОТЫ ВОЗБУЖДЕНИЯ

 

В. С. Власов1, В. Г. Шавров2, В. И. Щеглов2

1Сыктывкарский государственный университет

2Институт радиотехники и электроники им. В.А.Котельникова РАН

Статья получена 6 сентября 2015 г.

 

Аннотация. Рассмотрены вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. В случае, когда резонансная частота упругой подсистемы составляет кратную часть резонансной частоты магнитной, в сильно нелинейном режиме возбуждения возможно деление исходной частоты как в целочисленном, так и в дробном отношении. Рассмотрены случаи круговой и линейной поляризации возбуждающего поля. Выявлены различные режимы деления и предложены гипотезы для их интерпретации.

Ключевые слова: магнитострикционный преобразователь, нелинейные колебания, деление частоты.

Abstract. The forced vibrations of magnetization and elastic displacement in normal magnetized ferrite plate having magnetoelastic properties are investigated. In the case when resonance frequency of elastic system is equal to the multiple part of resonance frequency of magnetic system, in strong nonlinear regime of excitation it is possible the division of initial frequency in whole-number and also in fractional-number relation. It is investigated the cases of circular and linear polarization of excitation field. It is found the different regimes of division and supposed some hypotheses of its interpretation.

Key words: magnetostriction transducer, nonlinear vibrations, division of frequency.

 

Введение

Возбуждение ультразвуковых колебаний с помощью магнитострикционных преобразователей [1-4], кроме традиционных областей, таких как дефектоскопия, гидроакустика и медицина, весьма перспективно в акустоэлектронике, где высокая механическая добротность ферритовых резонаторов (до при использовании железоиттриевого граната (ЖИГ) ) позволяет создать высокоэффективные устройства обработки информации в диапазоне СВЧ ().

Первые экспериментальные работы по возбуждению гиперзвука с помощью магнитоакустических преобразователей на ЖИГ [5,6] выявили высокую эффективность возбуждения в сочетании с весьма малым затуханием. Однако вскоре было обнаружено [4,7], что высокие результаты достижимы лишь при мощности подводимого сигнала не более , из-за ограничения, налагаемого параметрическим возбуждением обменных спиновых волн [8-11]. Столь малая мощность препятствовала многим применениям, в первую очередь связанным с механическим воздействием гиперзвука на различные тела. Задача повышения мощности породила ряд работ [12-17], где было показано, что параметрический распад отсутствует в геометрии преобразователя в виде нормально намагниченного тонкого диска (пластины), низшая частота ферромагнитного резонанса (ФМР) которого совпадает с "дном" спектра обменных  волн.

Теоретически задача возбуждения гиперзвука с помощью магнитоакустического преобразователя на нормально намагниченной ферритовой пластине впервые была рассмотрена в линейном приближении в работах [3,4]. Некоторые особенности нелинейного приближения затронуты в работах [18,19], однако проведенное там рассмотрение, направленное в первую очередь на описание качественной картины, не позволило выявить предельные возможности возбуждения гиперзвука. Более подробное исследование, проведенное в работах [20,21], показало, что амплитуда гиперзвуковых колебаний, возбуждаемых на частоте ФМР, в нелинейном режиме может превышать амплитуду линейных колебаний почти на два порядка.

Такое возбуждение однако требовало совпадения частоты упругой резонансной системы с частотой ФМР, что для практических применений не всегда удобно. Некоторое расширение полосы возбуждения возможно путем использования двухслойной магнитной структуры [22], что обусловлено определенным разнесением частот ФМР отдельных слоев. Однако существенного выхода за пределы одной или двух рядом расположенных линий ФМР достичь не удается.

Тем не менее хорошо известно [23-25], что в сильно нелинейной колебательной системе возможно возбуждение эффективных колебаний большой амплитуды на частотах, находящихся вне основного резонанса, но ей кратных в целочисленном отношении. При этом кратное изменение частоты может происходить как вниз (деление), так и вверх (умножение).

Заметим, что тогда как умножение частоты достигается сравнительно простыми средствами, например путем выделения кратных гармоник нелинейного генератора, деление частоты представляет задачу значительно более сложную и требует применения специальных схем, содержащих умножитель частоты с последующим вычитающим устройством [24]. Несколько особняком стоит использование резонанса второго рода, также требующее особого вида нелинейности [23,26].   

Тем более интересным было бы рассмотреть вопрос о возможности использования нелинейного магнитострикционного преобразователя не только для умножения, но и особенно для деления частоты. Некоторые варианты такого исследования выполнены в работах [27-31], однако проведенное там рассмотрение является неполным. Так все внимание уделено только преобразованию частоты в промежуток времени между процессами релаксации магнитных и упругих колебаний, тогда как возможность преобразования за счет собственно нелинейности магнитных колебаний не рассмотрена. Не выявлена также роль поляризации возбуждающего прецессию намагниченности переменного поля.   

Настоящая работа является дальнейшим развитием, расширением  и углублением результатов, полученных в работах [27-31], и посвящена исследованию возможности кратного изменения частоты в обе стороны (вверх и вниз) гиперзвуковых колебаний, возбуждаемых магнитострикционным преобразователем, при подаче на него сигнала, соответствующего частоте ФМР. Учитывается как собственная нелинейность прецессии намагниченности, так и роль поляризации возбуждающего поля. Частоты возбуждаемых гиперзвуковых колебаний при этом делятся или умножаются как в целочисленном, так и в дробном отношении.  

Работа, ввиду значительного объема, состоит из двух частей.

В первой части (данная статья) рассматривается общая геометрия возбуждающей структуры магнитострикционного преобразователя и основной математический аппарат, а также деление частоты возбуждаемого гиперзвука по отношению к частоте ФМР. 

Во второй части (следующая статья) будет рассмотрено умножение частоты возбуждаемого гиперзвука по отношению к частоте ФМР.  

 

1. Геометрия задачи и основные уравнения

Геометрия задачи, совпадающая с принятой в [20,21], а также в [27,28], показана на рис.1. В ее основе лежит плоскопараллельная пластина толщины , обладающая магнитными, упругими и магнитоупругими свойствами. Материал пластины имеет кубическую кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью пластины.

 

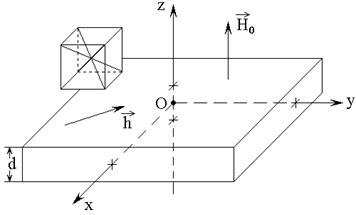
Рис.1. Геометрия задачи. Слева – схема кристаллографической ячейки.

 

Внешнее постоянное магнитное поле  приложено перпендикулярно плоскости пластины, переменное магнитное поле  действует в плоскости пластины. Задача решается в декартовой системе координат , плоскость  которой совпадает с плоскостью пластины, а оси ,  и  параллельны ребрам куба кристаллографической ячейки. Центр системы координат  находится в центре пластины, так что ее плоскости соответствуют координатам .

Уравнение движения для намагниченности (уравнение Ландау-Лифшица с диссипативным членом в форме Гильберта) [32-34] имеет вид: 

,                                           (1)

где   – нормированный вектор намагниченности,  – намагниченность насыщения,  – гиромагнитная постоянная (),   –  параметр затухания,  – эффективное поле, равное: 

,                                                                             (2)

где   – полная плотность энергии пластины, равная сумме плотностей магнитной, упругой и магнитоупругой энергий [32,33] (здесь оставлены только члены, важные для дальнейшего рассмотрения):

,   (3)

где:  – тензор деформаций, – константа (модуль) упругости,  – константа магнитоупругого взаимодействия.

Аналогично [20,21,27,28] получаем полную систему уравнений и граничных условий:

уравнения для компонент намагниченности :

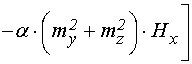                                            ;                             (4)

 

где уравнения для  и  получаются циклической перестановкой ,,;

уравнения для компонент упругих смещений :

,                                         (5)

где  – плотность материала пластины;   

граничные условия:

.                                                     (6)

Входящие в уравнение (4) эффективные поля  имеют вид:

;                                                                                      (7)

;                                                                                     (8)

,                                                               (9)

где  – внешнее постоянное поле,  – компоненты внешнего переменного поля, а выражения для компонент полей  аналогичны приведенным в работе [20,21,27,28] (магнитная анизотропия отсутствует, оставлены только слагаемые, важные для дальнейшего рассмотрения):

,            (10)

 

при этом  и  получаются из (10) циклической перестановкой ,,.

В дальнейшем будут рассмотрены два варианта поляризации переменного поля – круговая и линейная. При круговой поляризации правого направления вращения компоненты переменного поля имеют вид:

,         ,                       (11)

причем при точной круговой поляризации полагается .

При линейной поляризации компоненты переменного поля имеют вид:

,         ,                                                     (12)

что получается из формул (11) при .

Таким образом, в общей постановке задачи здесь имеются три уравнения первого порядка для намагниченности без граничных условий и два уравнения второго порядка с четырьмя граничными условиями по два на каждой границе. В соответствии с процедурой, описанной в работах [20,21], система уравнений (4)-(6) была приведена к эквивалентной системе из семи уравнений первого порядка без граничных условий, которая далее решалась численно методом Рунге-Кутта четвертого порядка [35]. Результаты такого решения приведены далее.

 

2. Основные параметры задачи 

При расчете использовались основные параметры материала, типичные для монокристалла ЖИГ: ; , однако для более наглядного выявления излагаемых далее результатов значение константы магнитоупругого взаимодействия было взято в несколько раз большим:, где  – целое число от 2 до 40, а . Для того, чтобы развитие колебаний до стационарной амплитуды происходило не более чем за 20-30 периодов (в пределах разрешения кривых на рисунке), параметры затухания магнитной и упругой подсистем были выбраны равными ,   (что также несколько больше типичных для монокристалла ЖИГ значений  и ). При таких параметрах время релаксации магнитных колебаний составляло около , а время релаксации упругих – . Остальные параметры задачи были выбраны такими, чтобы в отсутствие магнитоупругой связи при линейных колебаниях резонансные частоты однородной прецессии и первой моды упругих колебаний совпадали и равнялись . При этом постоянное поле составило , а резонансная толщина магнитной пластины . Переменное поле прикладывалось в плоскости пластины и имело круговую или линейную поляризацию. Другие параметры, используемые для построения кривых, указаны в подписях к рисункам и в тексте. Развитие колебаний рассматривалось во временном интервале  с шагом .

Для осуществления деления частоты система настраивалась таким образом, чтобы частота упругого резонанса пластины, определяемая ее толщиной, была в желаемом кратном отношении меньше частоты магнитного резонанса (ФМР), на которой производилось возбуждение,. С этой целью толщина магнитной пластины выбиралась в кратное число раз большей резонансной, то есть , где  – требуемая кратность. 

 

3. Два варианта процесса деления частоты

Предварительное рассмотрение показало, что деление и умножение частоты происходят принципиально различным образом, в зависимости от того, является ли поляризация возбуждающего поля круговой или линейной.

В случае круговой поляризации решающую роль играют процессы релаксации магнитных и упругих колебаний, а также соотношение их взаимного вклада в общие релаксационные процессы и баланс между их характерными временами. Поэтому для успешной реализации деления частоты в этом случае важно соотношение между моментом включения возбуждения и временем наблюдения явления.  

В случае линейной поляризации подобная зависимость отсутствует, так что устойчивое деление частоты наблюдается в любой момент времени, достаточно удаленный от момента включения возбуждения, в том числе при временах, значительно превышающих времена релаксации магнитной и упругой систем, когда амплитуды возбуждаемых колебаний устанавливаются на постоянном уровне.   

Ввиду принципиального различия участвующих в этих процессах механизмов, рассмотрим их по отдельности, то есть сначала обратимся к случаю круговой поляризации типа (11), а затем – к линейной типа (12).

 

4. Круговая поляризация поля возбуждения

Случай круговой поляризации наиболее прост с точки зрения прецессии намагниченности, так как здесь возбуждение является симметричным относительно направления постоянного поля и в отсутствие магнитоупругого взаимодействия прецессия намагниченности также является чисто круговой.

Столь высокая симметрия приводит к тому, что поле магнитострикции, возбуждающее упругие колебания, также имеет чисто круговую поляризацию, которая остается таковой при сколь угодно высоком уровне возбуждения.

В силу чистой линейности упругой системы, в установившемся режиме какие-либо условия для возбуждения ее на частоте более низкой, чем частота приложенного поля, полностью отсутствуют.  

Колебания на частоте собственного упругого резонанса, являющейся значительно ниже возбуждающей,  возможны только в переходном режиме, когда упругая система из состояния покоя начинает раскачиваться действующей на нее магнитной системой. Такая раскачка сопровождается биениями между частотами собственной и возбуждающей [23-25]. В этом случае в каком-то промежутке времени в упругой системе могут возникнуть колебания на ее собственной резонансной частоте. Это промежуток начинается тогда, когда магнитная система передает упругой настолько много энергии, сколько способна, то есть где-то незадолго до окончания времени релаксации магнитной системы. Заканчивается такой промежуток времени тогда, когда заканчиваются упомянутые биения, то есть после окончания времени релаксации упругой системы.  

То есть интервал времени, когда при круговой поляризации может реализоваться процесс деления частоты, заключен где-то между временами релаксации магнитной и упругой систем, при условии, конечно, что время релаксации упругой системы больше такового для магнитной системы.  

При принятых величинах параметров магнитного и упругого затухания (,  , раздел №2) время релаксации магнитных колебаний составляет около , а упругих – , поэтому интервал времени наблюдения будет заключен между этими значениями.

 

5. Деление частоты на два

В качестве примера рассмотрим наиболее простой случай деления частоты на два, для чего выберем толщину магнитной пластины вдвое больше той, которая соответствует резонансу на частоте возбуждения. При этом собственной резонансной частотой упругих колебаний будет половина от частоты переменного поля. Так, частоте возбуждения  соответствует упругий резонанс пластины толщиной . Получаемой в результате деления частоте  соответствует упругий резонанс пластины, толщиной вдвое большей: .

Будем рассматривать два режима возбуждения: линейный при  и сильно нелинейный – при  (напомним, что, согласно [20,21], переход от линейного к нелинейному режиму соответствует ). Поляризацию поля зададим круговой (11). Для большей наглядности рассмотрения константу магнитоупругого взаимодействия положим несколько большей, чем для ЖИГ, а именно: .

 

6. Роль нелинейности  

Рассмотрим сначала роль нелинейности колебательной системы, проявляющейся здесь при достаточно большой амплитуде возбуждения.

Предварительное исследование показало, что характер процесса деления частоты проявляется по разному, в зависимости от начального момента возбуждения. Обусловлено это тем, что процесс деления сопровождается двумя переходными режимами, связанными с релаксацией магнитных и упругих колебаний. Более подробно роль процессов релаксации рассмотрена в разделе №7, сейчас же отметим, что оптимальные условия деления наблюдаются по времени между характерными временами релаксации обоих видов, колебаний. По этой причине в настоящем разделе пределы развертки во времени были выбраны между этими временами в интервале от  до , то есть  когда релаксация магнитных колебаний уже закончилась, а релаксация упругих в достаточной степени еще не проявилась.

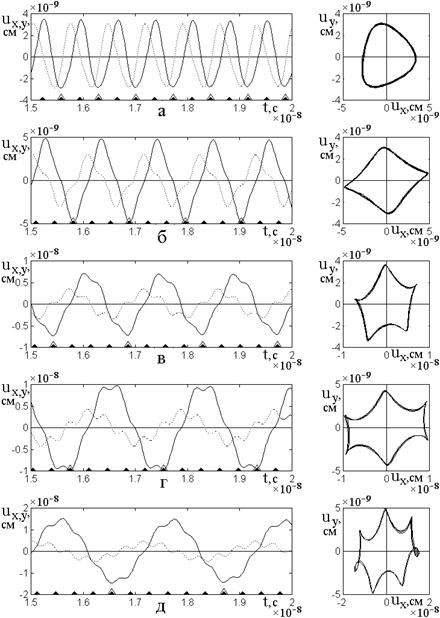
Соответствующее развитие колебаний во времени иллюстрируется рис.2.

 

Рис.2. Развертки во времени магнитных и упругих колебаний в пластине при различной толщине и уровне возбуждения. Сплошные линии – -компоненты, пунктирные линии – -компоненты.

а – ,  ;

б – ,  ;

в – ,  ;

г – ,  .

 

Из рис.2 видно, что в случае линейного возбуждения (а,б) как при одинарной (а), так и при двойной (б) толщине пластины частота как магнитных, так и упругих колебаний совпадает с частотой возбуждения, так что удвоение толщины пластины к делению частоты не приводит. То есть в этом случае наблюдается классический режим вынужденных колебаний на исходной частоте.

В случае нелинейного возбуждения (в,г) при одинарной толщине пластины (в) частота как магнитных, так и упругих колебаний остается равной частоте возбуждения. Однако при удвоенной толщине пластины (г), хотя частота магнитных колебаний (верхняя эпюра) по-прежнему совпадает с частотой возбуждения, но частота упругих колебаний (нижняя эпюра) уменьшается в два раза относительно частоты возбуждения.  

Таким образом, можно видеть, что для реализации эффекта деления частоты необходимыми условиями являются: соответствие толщины пластины резонансу на частоте, получаемой в результате деления, а также достаточно высокий уровень возбуждения обеспечивающий сильное проявление нелинейности системы.

Следует внести некоторую ясность в используемое здесь понятие «сильной» нелинейности. Дополнительное исследование показало, что при принятых в настоящем рассмотрении параметрах задачи (раздел №2) для эффективного деления частоты, без заметной (менее единиц процентов) примеси колебаний на основной частоте, необходим уровень возбуждения  более или порядка . По отношению к намагниченности насыщения ЖИГ () это составляет около  раз, а относительно подмагничивающего поля () – несколько меньше или примерно того же порядка. Такой уровень возбуждения резкого порога не имеет, однако переход от режима, подобного показанному на рис.2б, к режиму, представленному на рис.2г, происходит, хотя и достаточно плавно, но начинается и заканчивается в интервале не более  от указанного критического значения.

Возвращаясь к данным, представленным на рис.2, отметим, что дополнительным условием успешной реализации деления частоты является довольно критичный выбор интервала времени наблюдения относительно начала возбуждения, более подробно рассмотренный в следующем разделе.

 

7. Роль интервала времени

Поскольку, как отмечено в разделе №4, характер процесса деления частоты проявляется по разному в зависимости от начального момента возбуждения, выделим несколько характерных интервалов времени одинаковой протяженности, приходящихся на разные моменты относительно начала возбуждения.

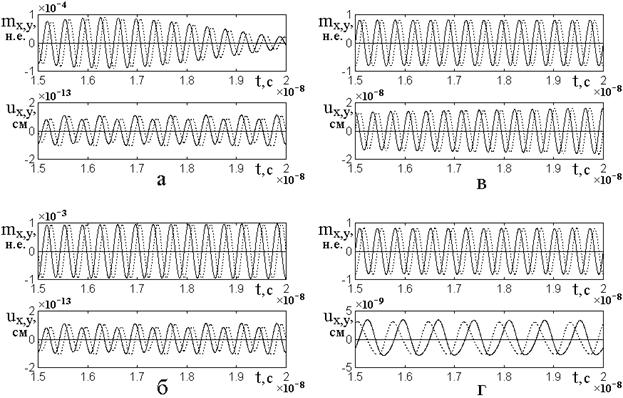
Соответствующее развитие колебаний во времени и отвечающие ему параметрические портреты иллюстрируются рис.3.

 

Рис.3. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты в различные промежутки времени от начала возбуждения. Деление частоты на два. Сплошные линии – -компоненты, пунктирные линии – -компоненты. Параметры: ,  .

а – ;

б – ;

в – ;

г – .

 

Из рис.3а видно, что сразу после включения возбуждения в интервале времени  магнитные колебания, имея выделенной частоту, близкую к частоте возбуждения, все же носят довольно беспорядочный характер. Это происходит из-за того, что сильное возбуждающее поле сразу приводит к ударному возбуждению системы, в результате чего происходят биения между свободными колебаниями магнитной и упругой систем в сочетании с частотой возбуждения. При времени около , близкого к времени релаксации магнитной системы, ее собственные колебания затухают, в результате чего вынужденные колебания заметно упорядочиваются.

Параметрический портрет имеет вид довольно широкого круглого кольца со слегка замазанной серединой. Завитки центральной замазки соответствуют постепенно релаксирующим биениям магнитных колебаний, размазка основного кольца – недостаточной упорядоченности вынужденных колебаний, не успевших еще полностью очиститься от биений.                 

Упругие колебания сразу после включения возбуждения имеют хорошо выраженный характер половинной частоты, то есть период их в два раза превышает период переменного поля. Некоторая нестабильность амплитуды, имеющая место до времени , обусловлена релаксационными биениями магнитных колебаний. Небольшая размазка параметрического портрета также соответствует этим биениям.    

Интервал времени , рассмотренный на рис.3б, выбран таким образом, что он находится примерно посередине между временами релаксации магнитных и упругих колебаний. То есть при этом магнитные колебания и связанные с ними биения уже затухли, а упругие, возбужденные ударным включением переменного поля, еще сохранили достаточно большую величину.  

Видно, что магнитные колебания носят чисто синусоидальный характер, синхронный с полем возбуждения. Соответствующий параметрический портрет имеет вид правильного узкого кругового кольца с отсутствием каких-либо следов биений.

Упругие колебания также имеют вид, довольно близкий к правильной синусоиде, их амплитуда во времени носит стабильный характер, однако параметрический портрет, имея узкую кольцевую форму, все же напоминает равносторонний треугольник с сильно скругленными углами. Такой вид параметрического портрета отражает примесь второй гармоники, на развертках во времени на глаз не заметной. То есть собственные упругие колебания все же еще недостаточно релаксировали, чтобы полностью повторять возбуждение, а сохраняют еще легкие следы биений.

Интервал времени , рассмотренный на рис.3в характерен тем, что свободные магнитные колебания уже достаточно давно затухли, тогда как упругие еще сохраняют некоторую амплитуду, однако меньшую, чем в интервале времени, показанном на рис.3б.

Видно, что здесь магнитные колебания имеют чисто вынужденный характер, а параметрический портрет имеет форму узкого правильного кругового кольца. То есть здесь повторяется та же картина, что и на рис.3б.

Однако упругие колебания сильно отличны. Собственные колебания уже почти затухли, так что на их место водворяются вынужденные колебания с частотой, равной частоте возбуждения. Периодичность пока еще сохраняется равной половинной частоте, но между основными максимумами дополнительные возвышения уже весьма заметны. Параметрический портрет имеет вид симметричного трехлепесткового «цветка», что соответствует сложению основной и половинной частот переменного поля. 

В интервале времени , рассматриваемом на рис.3г, все собственные колебания как магнитной, так и упругой систем полностью затухли, поэтому те и другие колебания имеют вид правильных синусоид с отсутствием каких-либо следов биений. Тот и другой параметрические портреты имеют вид правильных узких колец чисто круговой формы, что свидетельствует об установлении стационарного режима чисто вынужденных колебаний. 

Таким образом, с точки зрения осуществления правильного деления частоты при круговой поляризации возбуждения наиболее благоприятным является интервал времени, промежуточный между временами релаксации магнитных и упругих колебаний, иллюстрируемый рис.3б.  

Следующим этапом рассмотрения будет исследование деления частоты возбуждения в большем двух целочисленном и дробном отношении, предварительно рассмотренное в работах [27-31], к чему и перейдем далее.   

 

8. Деление в целочисленном отношении

Рассмотрим теперь другие возможности деления частоты, для чего обратимся к рис.4. Здесь показаны варианты деления частоты в целочисленном отношении к частоте возбуждения. Для осуществления деления толщина магнитной пластины выбиралась в целое число раз большей резонансной, соответствующей частоте ФМР, то есть то есть , где  – требуемая кратность. Рис.4а соответствует кратности равной двум, 4б – трем, 4в – четырем, 4г – пяти и 4д – шести. На нижнем крае эпюр треугольные точки соответствуют периодичности возбуждающего сигнала. Точки в треугольниках отмечают периодичность возбуждаемых упругих колебаний.

Из рисунка видно, что во всех случаях период упругих колебаний превышает период возбуждения в то самое число раз, во сколько толщина пластины превышает резонансную. При этом форма колебаний при делении на два и в какой-то степени на три довольно хорошо соответствует синусоидальной, а при дальнейшем увеличении кратности деления появляются искажения, связанные с возбуждением побочных колебаний, частота которых равна частоте возбуждения, а амплитуда составляет порядка  от максимальной. 

Амплитуда основных возбуждаемых колебаний с повышением кратности деления растет, так при  она составляет , при  – , при  – ,  при  –  , а при  – достигает . По-видимому, такой рост амплитуды обусловлен накоплением энергии возбуждаемых магнитных колебаний за время периода обусловленных ими упругих колебаний тем большим, чем отношение периодов больше. То есть энергия накапливается за несколько периодов магнитных колебаний, после чего разражается за один период упругих.

 

Рис.4. Развертки во времени для компонент упругого смещения и соответствующие им параметрические портреты при различной кратности деления частоты. Сплошные линии – компоненты , пунктирные линии – компоненты . Толщина пластины: а – ;  б – ;  в – ;  г – ;  д – .Переменное поле: .

 

Фазовый портрет упругих колебаний имеет вид криволинейного многоугольника с вершинами тем более острыми, чем кратность деления выше. Число вершин на единицу превышает кратность деления, что обусловлено девяностоградусным сдвигом фаз  и  компонент возбуждаемых колебаний, в сочетании с наложением на основные колебания небольшой добавки от составляющей частоты возбуждения. При этом основной «овал» цикла образуется за счет основной составляющей, а «острые вершины» – за счет добавки. Действительно, при  (4а) основные колебания почти синусоидальны, роль добавки ничтожна и вершины треугольника закруглены. При  (4б) добавка уже слегка заметна и вершины начинают обостряться. При дальнейшем увеличении кратности обострение вершин выражается сильнее, а при  (рис.4д) некоторые из них уже приобретают петлеобразную форму.

Заметим, что амплитуда  компоненты всегда несколько меньше амплитуды  компоненты, причем это различие с увеличением кратности увеличивается. Так при  амплитуда компоненты  составляет  от амплитуды , как при  не превышает . Заметим, что видимое сохранение высоты параметрического портрета при переходе от рис.4а к рис.4д является кажущимся и обусловлено различием масштабов по горизонтальной и вертикальной  осям. 

По-видимому, такое различие амплитуд  и  компонент упругого смещения вызвано кубической симметрией системы и отражает по мере увеличения кратности деления переход поляризации возбуждаемых упругих колебаний от круговой к эллиптической.

 

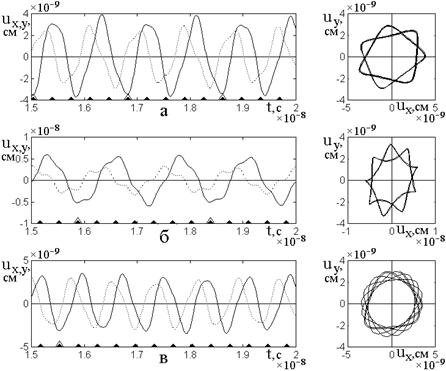
9. Деление в дробном отношении

Рассмотрим теперь деление частоты в дробном отношении, иллюстрируемое рис.5. Здесь рис.5а соответствует кратности промежуточной посередине между  и  равной , рис.5б – промежуточной посередине между  и  равной  , рис.5в – промежуточной с произвольным расположением между  и  равной .

 

Рис.5. Развертки во времени для компонент упругого смещения и соответствующие им параметрические портреты при различной кратности деления частоты. Сплошные линии – компоненты , пунктирные линии – компоненты . Толщина пластины: а – ;  б – ;  в – .

Переменное поле: .

 

Из рисунка видно, что деление частоты возможно и в этом случае, однако примесь составляющей частоты возбуждения сказывается сильнее, приводя к более заметному отклонению формы возбуждаемых упругих колебаний от синусоидальной.

Амплитуда возбуждаемых колебаний сохраняется близкой к амплитуде в случае целочисленного деления, причем соотношение амплитуд  и  компонент также меняется мало. Однако сильные изменения претерпевает параметрический портрет. Так в случае, когда кратность деления приходится на середину соседних целочисленных кратностей (рис.5а, 5б), параметрический портрет принимает вид многовершинного криволинейного многоугольника, образуемого двукратным прохождением одного периодического цикла. В результате такого двукратного прохождения количество острых вершин многоугольника получается равным сумме от количеств вершин многоугольников, образуемых соседними целочисленными значениями кратности. Так для портрета на рис.5а, построенного при , где соседние кратности равны  и , которым соответствуют числа вершин  и  соответственно, суммарное число вершин получается равным . Аналогичный подсчет для  (рис.5б) дает  вершин, что и наблюдается на рисунке.

При кратности, выражаемой произвольным дробным числом, количество вершин увеличивается тем сильнее, чем больше число кратности отличается от соседних целых чисел, в результате чего фазовый портрет приобретает вид «замазанного» траекториями широкого кольца почти правильной формы. Такой случай иллюстрируется рис.5в, где кратность выбрана равной . Видно, что некоторые траектории образуют цикл, близкий к случаю  (утолщенная линия), тогда как остальные распределяются по кольцу более или менее равномерно.

Таким образом, можно сделать вывод, что деление частоты упругих колебаний возможно при любой кратности деления, определяемой отношением действительной толщины пластины к резонансной, однако правильность формы получаемых колебаний с увеличением кратности деления и отклонением ее от целочисленных значений ухудшается.

 

10. Оптимальное соотношение времен релаксации

Описанные выше случаи деления частоты предполагают, что колебания упругой системы происходят таким образом, что заметное изменение их амплитуды, обусловленное релаксацией, происходит за время, во много раз превышающее период самих колебаний. При этом магнитные колебания релаксируют еще до начала установившегося деления, когда переходный процесс вызывает резкие искажения формы колебаний. После стабилизации формы колебаний, то есть по завершению релаксации магнитной подсистемы, более или менее правильные колебания, соответствующие разделенной частоте, продолжаются почти до окончания времени релаксации упругой подсистемы. При этом амплитуда разделенных колебаний постепенно снижается в соответствии с экспоненциальным законом с показателем, соответствующим времени релаксации упругих колебаний.   

На рис.4 и 5 такое уменьшение амплитуды не заметно из-за того, что время регистрации колебаний выбрано значительно меньшим времени релаксации упругой подсистемы. Так в рассмотренных случаях время релаксации магнитных колебаний составляет около , а время релаксации упругих – около , то есть на порядок больше. Время развертки на рисунках выбрано в  раз меньшим времени релаксации упругих колебаний, что и приводит к незначительности изменения амплитуды за этот период.

Оптимальные реализованные в настоящей работе условия наблюдения эффекта деления частоты в материале, подобном ЖИГ, сводятся к следующим: ;    ;    ;    ;    ;    .

 

11. Гипотеза ударного возбуждения упругой системы

Дополнительные исследования показывают, что в рассматриваемом случае круговой поляризации возбуждения  устойчивое деление частоты с сохранением постоянства амплитуды на протяжении неопределенно долгого промежутка времени возможно только при бесконечно малом параметре затухания упругой подсистемы. Когда же параметр упругого затухания конечен, устойчивые колебания разделенной частоты происходят только в течение времени релаксации упругой подсистемы, после чего форма колебаний постепенно искажается, приближаясь к форме колебаний возбуждения, то есть, можно сказать, что деление вырождается, переходя в простые вынужденные колебания с частотой возбуждения.  

Такое поведение колебаний разделенной частоты, по-видимому, обусловлено тем, что в начальный момент времени происходит как бы ударное возбуждение упругой подсистемы за счет связи с магнитной, продолжающееся в течение времени релаксации магнитной подсистемы. При этом упругая система начинает колебаться с частотой собственного резонанса, что и наблюдается как деление частоты исходных колебаний. Такие собственные колебания постепенно затухают в течение промежутка времени, соответствующего релаксации упругой системы, после чего эффект деления пропадает и остаются только вынужденные колебания с частотой вынуждающей силы.    

Такое ударное возбуждение упругой системы происходит только в сильно нелинейном режиме, когда амплитуда магнитных колебаний резко возрастает за незначительный промежуток времени, определяемый не столько временем релаксации магнитной системы, сколько крайне высокой амплитудой возбуждающего сигнала. В линейном режиме нарастание магнитных колебаний происходит за время, определяемое именно временем магнитной релаксации, поэтому эффективность ударного возбуждения упругой системы значительно снижается и эффект деления частоты пропадает, как это и наблюдается на рис.2а,б.  

 

12. Линейная поляризация поля возбуждения

Случай линейной поляризации наиболее интересен тем, что здесь  деление частоты с процессами релаксации никак не связано и происходит в установившемся стационарном режиме при любом времени, прошедшем после включения возбуждения.

Поэтому далее будет рассмотрен интервал времени наблюдения, достаточно удаленный от начала колебаний, то есть такой, расположение которого значительно превышает времена релаксации как магнитных, так и упругих колебаний.

При принятых величинах параметров магнитного и упругого затухания (,  , раздел №2) время релаксации магнитных колебаний составляет около , а упругих – , поэтому положим интервал времени наблюдения следующим: , где, согласно рис.3г, деление частоты при круговой поляризации возбуждения уже отсутствует.

 

13. Деление частоты на два

Как отмечено в предыдущем разделе, линейная поляризация переменного поля обеспечивает принципиально другое поведение магнитоупругой системы, отличающееся от случая круговой поляризации. Здесь принципиальную роль приобретает абсолютная величина константы , обеспечивающей связь между магнитной и упругой подсистемами. Как и ранее, сначала рассмотрим наиболее простой случай деления частоты на два. Развертки во времени магнитных и упругих колебаний для этого случая иллюстрируется рис.6. Рассмотрены линейное (а,б) и нелинейное (в,г) возбуждение, причем в каждом из этих случаев выбраны два значения константы магнитоупругости: малое (а,в) и большое (б,г).  

 

Рис.6. Развертки во времени магнитных и упругих колебаний в пластине при различной величине константы  и уровне возбуждения.

Толщина пластины , частота возбуждения .

Сплошные линии – -компоненты, пунктирные линии – -компоненты.

а – ,  , ;

б – ,  , ;

в – ,  , ;

г – ,  , .

 

Из рис.6а видно, что при малом возбуждающем поле и малой константе взаимодействия как магнитные (верхняя эпюра), так и упругие (нижняя эпюра) колебания имеют чисто синусоидальный характер. Компоненты  и , а также  и  в точности повторяют друг друга, отличаясь лишь сдвигом по фазе на , то есть здесь картина колебаний является чисто линейной и полностью классической. В упругих колебаниях составляющая половинной частоты полностью отсутствует. 

На рис.6б, в отличие от рис.6а, константа магнитоупругого взаимодействия увеличена в пять раз (до , однако как форма колебаний, так и взаимное соотношение их компонент по сравнению с предыдущим рисунком не изменились. Компоненты по-прежнему повторяют друг друга и сдвиг фазы между ними составляет те же . Единственным отличием является увеличение амплитуды упругих колебаний примерно в пять раз, то есть в том же соотношении, что и увеличение константы . Здесь также, как и в предыдущем случае, возбуждение упругих колебаний на частоте вдвое ниже возбуждающей полностью отсутствует. 

То есть можно сделать вывод, что при линейном возбуждении деление частоты места не имеет, причем характер как магнитных, так и упругих  колебаний от величины константы магнитоупругости не зависит.

Замечание. Предварительное исследование однако показывает, что упомянутое отсутствие зависимости имеет место лишь до значений константы порядка , выше которого наступает переориентация вектора намагниченности от нормали к плоскости пластины, подобная описанной в работе [36]. Заметим, что процессы переориентации могут составить тему для отдельного исследования и их изучение в рамки настоящей работы не входит.    

Рис.6в относится к случаю значительного возбуждающего поля, но довольно малой константы . Здесь наблюдается сильное искажение формы как магнитных (верхняя эпюра), так и упругих (нижняя эпюра) колебаний, сдвиг по фазе на  хотя и сохраняется, но амплитуда и огибающая колебаний отдельных компонент существенно различаются. Особенно заметное различие приобретают компоненты упругих колебаний (нижняя эпюра). Здесь не только взаимная амплитуда меняется более чем в три раза, но и центр колебаний -компоненты смещается от нуля по рисунку вверх, достигая величины , сравнимой с полной амплитудой колебаний этой компоненты. Заметим, что подобное различие между  и  компонентами обусловлено тем, что линейная поляризация возбуждающего поля имеет место вдоль оси  (подобно (12)). Проверка показывает, что при замене поляризации возбуждающего поля с оси  на ось  взаимное соотношение компонент как намагниченности, так и упругого смещения меняется местами на противоположное.

Важно отметить, что и в этом случае, как и в двух разобранных предыдущих, какие-либо следы возбуждения упругих колебаний половинной частоты полностью отсутствуют. То есть даже и в сильно нелинейном режиме такое значение константы взаимодействия, как , для реализации процесса деления частоты является недостаточным.

На рис.6г показано развитие колебаний в случае сильного возбуждения в сочетании со значительной величиной константы , в пять раз большей, чем на предыдущем рисунке (то есть ). Можно видеть, что здесь характер магнитных колебаний, хотя и изменился, но в довольно небольшой степени: амплитуда сохранилась приблизительно той же, несколько (раза в три) увеличились лишь промежуточные максимумы между основными пиками, соответствующие возбуждению второй гармоники за счет сильной нелинейности процесса. Однако характер упругих колебаний изменился совершенно радикальным образом. Так амплитуда их возросла почти на два порядка (точнее – в  раз), а период увеличился как раз вдвое, то есть произошел весьма сильно выраженный процесс деления частоты на два. Сдвиг компонент  и   между собой по фазе остался на те же , а соотношение амплитуд уменьшилось с трех до приблизительно  раза. Проверка показывает, что такое взаимное неравенство амплитуд, как и в предыдущем случае, обусловлено поляризацией возбуждающего поля вдоль оси  и при замене поляризации на ось  меняется на обратное.

Важнейшим характерным отличием данного случая от трех предыдущих является ярко выраженная реализация процесса деления частоты, в остальных случаях отсутствующая. То есть можно сделать вывод, что для реализации такого процесса является необходимым сочетание двух условий: сильного нелинейного возбуждения и значительной величины константы магнитоупругого  взаимодействия.

Замечание. Важно отметить, что в общем случае достижение этих двух условий не является резко пороговым. Во всяком случае, на данном этапе исследования контрольная проверка резкого порогового характера описанного здесь процесса деления частоты не выявила. Можно отметить лишь, что при принятых параметрах задачи (раздел №2) уровень возбуждения должен превышать  (что подобно уровню возбуждения при круговой поляризации, рассмотренному в разделе №6), а величина константы магнитоупругого взаимодействия должна превышать таковую для ЖИГ не менее чем в  раз. Таким образом, при плавном увеличении амплитуды возбуждения и константы взаимодействия выше указанных значений, переход от рис.6а к рис.6г происходит путем последовательных накоплений изменения формы тех и других колебаний, проходя через ряд промежуточных состояний, в некоторых случаях даже в какой-то степени напоминающих хаотический характер. Весьма разнообразные трансформации претерпевает параметрический портрет, на данном этапе не изучавшийся. Подробное рассмотрение таких промежуточных состояний, возможно, представляющих заметный интерес, требует отдельного исследования и в рамки настоящей работы не входит. 

 

14. Деление в целочисленном отношении

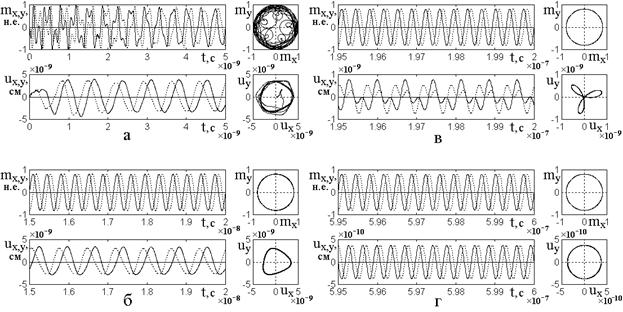
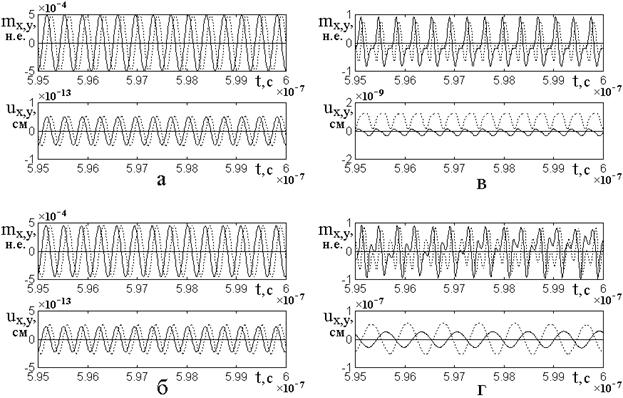
Рассмотрим теперь деление частоты возбуждения в более общих случаях. Сначала обратимся к более простому делению в целочисленном отношении. Соответствующие развертки во времени колебаний намагниченности и упругого смещения, а также их параметрические портреты, показаны на рис.7. 

 

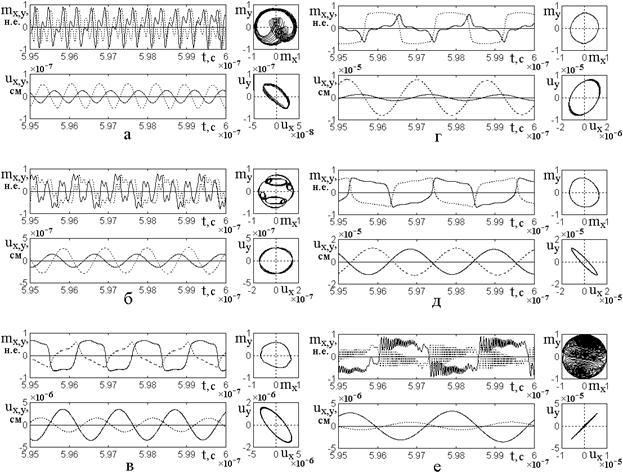
Рис.7. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты при различной кратности деления  в целочисленном отношении. Толщина: , где . Поляризация возбуждения линейная: , . Сплошные линии – -компоненты, пунктирные линии – -компоненты.

Кратность деления:  а – ;   б – ;   в – ;   г – ;

д – ;   е – .

Константа магнитоупругости:   а,б, … , д – ,

е  – .

 

 15. Различные режимы колебаний

Из рассмотрения рис.7 можно видеть, что по мере увеличения кратности деления имеют место три характерных режима колебаний. Рассмотрим их по очереди.

Режим №1. Этому режиму соответствуют рис.7а,б, кратность деления для которых равна  (а) и  (б). Такую кратность условно будем называть малой. В этом режиме характер поведения магнитной системы определяется главным образом полем возбуждения, поэтому условно его назовем «определяемым возбуждением». Колебания намагниченности происходят с частотой возбуждения, однако наблюдается некоторая примесь второй (а) и даже третьей (б) гармоник, увеличивающаяся по мере увеличения кратности деления. Параметрический портрет представляет собой круг с одним (а) или несколькими (б) слегка размазанными «завихрениями» к центру, отражающим примесь упомянутых гармоник. Колебания упругого смещения происходят с частотой, получаемой от деления частоты возбуждения на коэффициент кратности. Так на рис.7а она составляет половину частоты возбуждения, на рис.7б – одну треть. Колебания имеют чисто синусоидальный характер без какой-либо наблюдаемой примеси высокочастотных гармоник. Параметрический портрет представляет собой почти правильный эллипс, вытянутость осей которого определяется соотношением амплитуд компонент  и , а наклон относительно осей координат отражает относительный сдвиг фазы этих компонент приблизительно на . 

Режим №2. Этому режиму соответствуют рис.7в,г,д, кратность деления для которых равна  (в),  (г) и (д). Такую кратность условно будем называть средней. В этом режиме характер поведения магнитной системы определяется навязываемыми через посредство магнитоупругости колебаниями упругого смещения, частота которых получается как частное от деления частоты возбуждения на коэффициент кратности. То есть как магнитные, так и упругие колебания имеют одну и ту же частоту, равную задаваемой толщиной пластины частоте ее упругого резонанса на первой моде. Таким образом, этот режим можно условно назвать «определяемым упругостью». Форма колебаний намагниченности приближается к прямоугольной или в некоторых случаях пилообразно-треугольной с плавно закругленными углами. Такое поведение говорит о присутствии значительного числа (порядка  или более) высокочастотных гармоник, амплитуда которых однако является столь малой, что основные колебания остаются достаточно плавными. Сдвиг фазы колебаний компонент намагниченности друг относительно друга всегда составляет . Параметрический портрет представляет собой почти правильный круг, с некоторыми искажениями, определяемыми примесью высших гармоник. Упругие колебания по-прежнему имеют правильную синусоидальную форму, а параметрический портрет – такой же эллипс, раскрыв и наклон которого определяются соотношением амплитуд и фаз компонент  и . Отметим, что для случая кратности деления (г), то есть нечетной, сдвиг фаз этих компонент близок к , тогда как для кратности (в) и (д), то есть четной,  составляет почти .

Режим №3. Этому режиму соответствует рис.7е, кратность деления для которого равна . Такую кратность условно будем называть большой. В этом режиме основная  составляющая колебаний магнитной системы также определяется навязываемыми через посредство магнитоупругости колебаниями упругого смещения, частота которых получается как частное от деления частоты возбуждения на коэффициент кратности. Форма колебаний основной составляющей близка к прямоугольной, а относительный сдвиг фазы компонент  и  равен . Однако здесь, в отличие от режима №2, такие основные колебания не являются плавными, а сопровождаются большим количеством значительно более высокочастотных колебаний, что говорит о присутствии множества высокочастотных гармоник, частота которых превышает основную на порядок и более. Магнитные колебания ведут себя так, как будто бы в начальный момент перемагничивания, соответствующий началу прямоугольного импульса основной составляющей, ударным образом возбуждаются колебания, частота которых превышает частоту возбуждения во много (не менее семи-девяти) раз. Амплитуда таких высокочастотных колебаний в первый момент их возбуждения близка к перепаду намагниченности на фронте импульса, после чего плавно спадает, на протяжении прямоугольного импульса основной составляющей приближаясь к нулю. На спад амплитуды таких высокочастотных колебаний накладывается небольшая (около ) примесь частоты возбуждения. То есть колебания намагниченности здесь происходят с наличием большого числа высокочастотных гармоник, вследствие чего такой режим можно условно назвать «мультигармоническим» . Параметрический портрет для намагниченности здесь представляет собой почти правильный круг, практически полностью замазанный до самой середины за счет примеси высокочастотных гармоник. Однако и в этом случае упругие колебания по-прежнему имеют правильную синусоидальную форму, а параметрический портрет – такой же эллипс, раскрыв которого довольно мал (соотношение осей – около пяти) из-за сильного различия амплитуд компонент смещения  и . Сдвиг фазы между этими компонентами составляет около , что не подчиняется отмеченному для режима №2 соотношению четности.

Заметим однако, что из сопоставления параметрических портретов для упругости, представленных на рис.7а,в,д с рис.7б,г,е можно видеть что в первых трех случаях, когда кратность деления является четной (, , ), большая ось эллипса расположена во второй и четвертой четвертях координатной плоскости, а в других  трех случаях, где кратность нечетная (, , ) – в первой и третьей четвертях координатной плоскости. Такое расположение оси эллипса отражает соотношение фаз компонент упругого смещения, явно здесь связанное с четностью и нечетностью коэффициента деления.   

Итак, из проведенного рассмотрения можно видеть, что различие режимов в первую очередь состоит в изменении формы колебаний намагниченности. Колебания упругого смещения во всех этих случаях имеют правильную синусоидальную форму с частотой, определяемой толщиной пластины, то есть равной частному от деления частоты возбуждения на коэффициент кратности.

 

16. Роль величины константы магнитоупругости

Подробное исследование показывает, что проявление того или другого из описанных режимов напрямую с коэффициентом кратности деления не связано. Все три режима могут иметь место при любом из исследованных коэффициентов (от одного до семи). Реализация того или иного режима определяется соотношением между амплитудой возбуждения и величиной константы магнитоупругого взаимодействия . 

Так, как отмечено ранее в разделе №13, для реализации деления вообще, требуется наличие достаточно большой амплитуды возбуждения, составляющей не менее трех-пяти раз от намагниченности материала пластины, а также близкой по величине к значению подмагничивающего поля. То есть вектор намагниченности в процессе своего прецессионного движения должен отклоняться от нормали к плоскости пластины на углы не менее  градусов.

При принятой в настоящей работе амплитуде переменного поля  такой угол составляет порядка . При этом дополнительным условием является достаточно большая величина константы магнитоупругого взаимодействия. Так для деления частоты на два величина  еще не достаточна. В интервале  деление реализуется, причем при плавном увеличении константы наступает сначала режим №1, затем сменяющий его режим №2, после чего – режим №3. При  устойчивые колебания хаотизируются, амплитуда их в отдельные моменты времени достигает единицы, так что реализация деления частоты срывается.

С физической стороны такой срыв представляет собой экспоненциальное нарастание амплитуды магнитных колебаний, заканчивающееся укладыванием вектора намагниченности в плоскость пластины, после чего колебания прекращаются.

Переход между режимами №1-3 при увеличении  резкого порога не имеет, то есть происходит достаточно плавным образом. Также и срыв деления происходит в интервале  от среднего значения . Само значение константы срыва  определяется кратностью деления и с возрастанием кратности уменьшается. Так при делении на два оно составляет , при делении на три –  , при делении на пять – уменьшается до , а при делении на семь – падает до .

Таким образом, режим №1 реализуется при значении константы , достаточно далеком от срыва (примерно в два раза меньшем), режим №2 – при значении константы около полутора раз меньшем значения срыва и режим №3 – в непосредственной близости к срыву.    

 

17. Деление в дробном отношении

Рассмотрим теперь случай деления частоты возбуждения в дробном отношении, иллюстрируемый рис.8. Здесь левый столбец рисунков построен при целых значениях коэффициента деления, а правый – при дробных, увеличенных на  по сравнению со значениями левого столбца. Такое соотношение коэффициентов деления позволяет более наглядно выявить особенности, вносимые дробным характером этих коэффициентов по сравнению с близкими целыми значениями.  

Из рис.8 можно видеть, что при дробных коэффициентах имеют место те же режимы колебаний, что и при целых. Из сравнения рис.8г с рис.8а видно, что в обоих случаях реализуется режим №1. При этом колебания компоненты  (сплошные линии) становятся более близкими к чистой синусоиде, однако колебания компоненты  (пунктир) содержат в несколько большей степени примесь второй гармоники, в результате чего параметрический портрет приобретает несколько больше внутренних завитков (вместо одного – два или три). Однако в любом случае намагниченность колеблется с частотой возбуждения, то есть реализуется режим №1. 

 

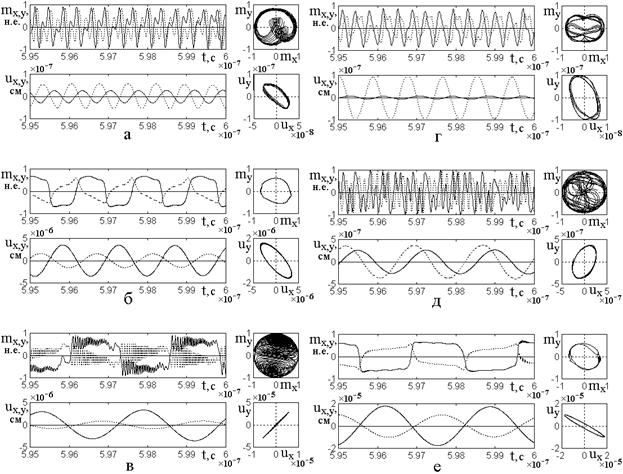
Рис.8. Развертки во времени магнитных и упругих колебаний, а также их параметрические портреты при различной кратности деления  в дробном отношении.  Толщина: , где .  Поляризация возбуждения линейная: , .  Сплошные линии – -компоненты, пунктирные линии – -компоненты.

Коэффициент кратности деления: а – ;  б – ;  в – ;  г – ;  д – ;  е – .

Константа магнитоупругости: а, б, г, д – ,
в, е – .

 

Из сравнения рис.8д с рис.8б видно, что в случае целочисленного деления (б) реализуется в чистом виде режим №2, тогда как в случае дробного (д) колебания намагниченности не испытывают навязывающего влияния колебаний упругости, так что, хотя и имеют место довольно сильные составляющие второй и третьей гармоник, но основная составляющая с частотой возбуждения сохраняется, то есть наблюдаемый характер колебаний следует отнести к режиму №1. Таким образом, здесь при переходе от кратности деления  (б) к кратности  (д) наблюдается понижение номера режима на единицу. Дополнительное исследование показывает, что здесь критическое значение константы магнитоупругости, соответствующее срыву, составляет около , что несколько больше значения при целом коэффициенте .

Из сравнения рис.8е с рис.8в видно, что в случае целочисленного деления (в) реализуется режим №3, тогда как в случае дробного (е) – совершенно четко выраженный режим №2. То есть и здесь при переходе от целой кратности (в) к дробной   (е) происходит понижение номера режима на единицу. В этом случае, аналогично предыдущему, критическое значение константы срыва также несколько повышается: с , соответствующего  до , соответствующего .

Упругие колебания во всех рассматриваемых случаях, как и при делении в целочисленном отношении, сохраняют чистый синусоидальный характер, однако соотношение амплитуд и фаз заметно меняется, что проявляется в изменении раскрыва и наклона эллипса параметрического портрета в правых столбцах рисунка по сравнению с левыми.

Таким образом, можно сделать вывод, что при делении частоты возбуждения в дробном отношении для колебаний намагниченности реализуются все те же режимы колебаний с той же последовательностью относительно значения кратности, что и при делении в целом отношении, с тем однако отличием, что значение константы срыва несколько повышается (на ) тем сильнее, чем кратность деления выше. 

При этом характер упругих колебаний всегда остается синусоидальным с некоторым изменением соотношения амплитуд и фаз компонент смещения. 

 

18. Множественный характер смены режимов

Рассмотренные выше случаи деления частоты возбуждения в целочисленном и дробном отношениях относятся к тому интервалу изменения константы магнитоупругого взаимодействия , в котором характер магнитных колебаний при изменении этой константы меняется достаточно плавно. Во всех случаях по мере увеличения константы режимы колебаний сменяют друг друга в возрастающем порядке. То есть при малом значении константы имеет место режим №1, при среднем – режим №2, при несколько большем – режим №3, при еще большем колебания претерпевают срыв.

Подробное исследование однако показывает, что таким первичным срывом дело не заканчивается, так что при дальнейшем увеличении константы снова могут реализоваться режимы №2 и №3, после чего может опять наступить новый срыв, по окончании которого снова реализуются режимы №2 и №3 и так далее. То есть чередование срыва, перемежающегося режимами №2 и №3, носит множественный характер.

 

Таблица №1.

 

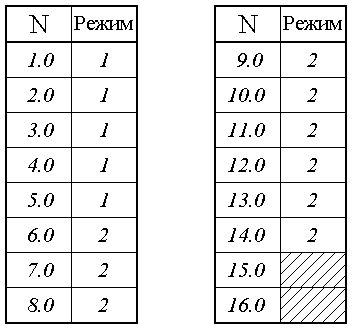
Общее представление о смене режимов при увеличении константы  дают таблицы №2 и №3, построенные при кратности деления равной четырем. В левых столбцах таблиц представлены коэффициенты , показывающие, во сколько раз принятое значение константы  превышает значение константы . В правых столбцах представлены соответствующие номера режимов. Режим срыва показан наклонной штриховкой, означающей, что при этом регулярные колебания намагниченности отсутствуют. Для удобства представления в формате страницы текста обе таблицы разбиты на части, непрерывно продолжающие друг друга.

Из таблицы №1 видно, что при  изменении от  до  имеет место режим №1, после чего вплоть до  он сменяется режимом №2. При  наступает первичный срыв. Подробная проверка показывает, что везде до первичного срыва характер режима колебаний меняется плавно, то есть при любых значениях  меньших  имеет место режим №1, а при любых  между  и  – режим №2. 

 

Таблица №2.

 

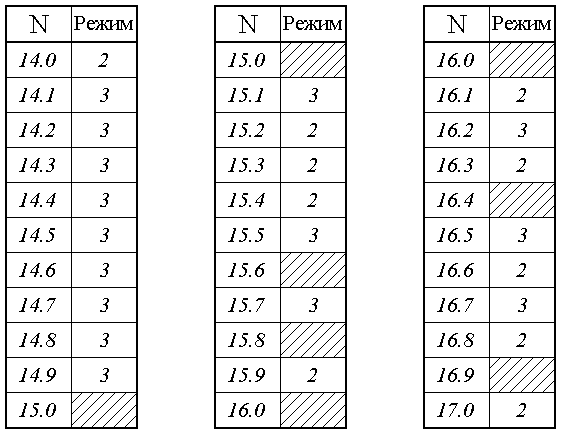
После первичного срыва, соответствующего , при  срыв также имеет место, однако между этими значениями срыв перемежается стационарными режимами. Более подробно изменение режимов при увеличении  более , иллюстрируется таблицей №2.

Из этой таблицы можно видеть, что при  имеет место еще режим №2, однако уже при  он сменяется режимом №3, который продолжается до , после чего при  наступает первичный срыв. Однако уже при  этот срыв сменяется режимом №3, который при  переходит в режим №2, продолжающийся до . При  на смену этому режиму приходит режим №3, после чего  при  снова происходит срыв. Этот срыв при  сменяется режимом №3, а затем новым срывом при , который при  переходит в режим №2 и так далее.

Таким образом, только до первичного срыва смена режимов происходит достаточно плавно, а при дальнейшем увеличении константы  срывы и режимы №2 и №3 чередуются, сменяя друг друга. Смена эта происходит довольно беспорядочным образом, так что после пары далеко расположенных друг от друга срывов при  равном  и  следуют несколько срывов, идущих друг за другом почти рядом – при ,  и , после чего промежуток снова увеличивается до , а затем становится еще больше и так далее. Подробная проверка показывает, что такой множественный квазихаотический порядок следования срывов, разделяемых режимами №2 и №3, имеет место вплоть до , когда вектор намагниченности уже приближается к плоскости структуры настолько, что наступает переориентация, подобная описанной в работе [36].

Упругие колебания во всех этих случаях, кроме достаточно узких участков срыва, сохраняют практически чистый синусоидальный характер с частотой в четыре раза ниже частоты возбуждения, однако их амплитуда и особенно фаза внутри интервалов между соседствующими срывами может сильно меняться. Так например, режим срыва, соответствующий  заканчивается при  и сменяется режимом №2. При этом сдвиг фазы между компонентами упругого смещения  и  при  составляет , а при  возрастает до . В этом случае соотношение амплитуд также меняется с  при  до  при .  

Заметим, что столь сильные изменения фазы и амплитуды упругих колебаний при относительно небольшом изменении константы  не сопровождаются столь же сильным изменением параметров колебаний намагниченности, то есть при  и при  реализуется один и тот же режим №2 с изменениями весьма незначительными.

 

19. Гипотеза двухрезонаторного характера системы

В качестве модели наблюдаемых явлений можно полагать, что здесь мы имеем дело с двухрезонаторной системой, один из резонаторов которой – магнитный, является сильно нелинейным, тогда как другой – упругий, всегда остается чисто линейным. Колебания намагниченности при достаточной амплитуде возбуждения, благодаря нелинейности своего резонатора, обогащаются гармониками, что проявляется в смене режимов. В это же время, колебания упругого смещения, благодаря линейности своего резонатора, гармоник  не приобретают, а остаются чисто синусоидальными. Можно сказать, что упругий резонатор здесь работает как узкополосный фильтр, настроенный на единственную частоту (свою первую упругую моду), в результате чего синусоидальный характер колебаний выдерживается весьма точно, а обилие гармоник, поступающих через магнитоупругую связь из магнитного резонатора, приводит к чувствительному изменению амплитуды и сдвигу фазы колебаний.

За разнообразие режимов и срыв магнитных колебаний опять-таки отвечает его нелинейность, однако теперь в общих колебаниях приобретает участие также и упругая система. Дополнительная проверка показывает, что при принятой амплитуде возбуждения  (при ), даже в отсутствие магнитоупругой связи, то есть при  колебания намагниченности все же не приобретают полностью устойчивый синусоидальный характер, а их амплитуда частично флуктуирует с величиной, достигающей  от максимума. Период следования флуктуаций составляет незначительную часть (не более ) от времени релаксации магнитной системы. Флуктуации прекращаются при уменьшении амплитуды возбуждения ниже , что близко к величине, необходимой для реализации процесса деления частоты. Важно  отметить, что флуктуирующий характер колебаний намагниченности свойственен только линейной поляризации возбуждающего поля, а при круговой, то есть при магнитные колебания полностью стабильны.

Можно полагать, что именно такой слегка флуктуирующий характер колебаний намагниченности при линейной поляризации возбуждения ответственен за возможность осуществления деления частоты в непрерывном режиме времени. То есть здесь за счет быстрого флуктуирующего изменения амплитуды колебаний намагниченности все время происходит некоторая небольшая «подзарядка» ударного возбуждения упругих колебаний, сливающаяся в один непрерывный синусоидальный режим на частоте упругого резонанса, определяемого толщиной пластины, что и представляет собой реализацию деления частоты возбуждения.  

Отличие от случая круговой поляризации (раздел №7) состоит здесь в том, что флуктуации намагниченности обеспечивают непрерывное повторяющееся во времени ударное подвозбуждение упругих колебаний, тогда как при круговой поляризации флуктуации намагниченности отсутствуют, так что там ударное возбуждение происходит только один раз в начале включения возбуждающего поля.  

Замечание. Заметим, что наблюдаемое в настоящей работе свойственное линейной поляризации переменного поля флуктуирующее изменение амплитуды намагниченности имеет место только при очень большой амплитуде возбуждения (как указано выше – при ). Такое поведение намагниченности при умеренной амплитуде возбуждения, типичной для исследования сильно нелинейного ФМР (не более ), в известной авторам литературе ранее не отмечалось. Можно полагать, что такого рода флуктуации не укладываются в классическую картину ФМР [33,34], так что природа их, по-видимому, требует более подробного исследования, на данный момент выходящего за рамки настоящей работы.

 

Заключение

Применительно к геометрии магнитострикционного преобразователя рассмотрены связанные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами, возбуждаемые переменным магнитным полем, частота которого совпадает с частотой ферромагнитного резонанса магнитной подсистемы. 

Показано, что в случае, когда резонансная частота упругой подсистемы составляет кратную часть от резонансной частоты магнитной подсистемы, возможно возбуждение упругих колебаний на частоте, соответствующей частоте упругого резонанса, что представляет собой процесс деления исходной частоты в кратном отношении.

Рассмотрены два варианта реализации деления частоты: первый – при возбуждении переменным полем круговой и второй – линейной поляризации.

Для случая круговой поляризации на примере деления частоты на два выявлена роль нелинейности магнитной системы и отмечен интервал времени, где процесс деления происходит наиболее эффективно. Показано, что наиболее благоприятным является интервал времени, промежуточный между временами релаксации магнитных и упругих колебаний. Отмечено, что необходимыми условиями для реализации эффекта деления частоты являются: соответствие толщины пластины резонансу на частоте, получаемой в результате деления, а также достаточно высокий уровень возбуждения обеспечивающий сильное проявление нелинейности магнитной системы.

Рассмотрено деление частоты в целочисленном и дробном отношении вплоть до коэффициентов деления от 1 до 6. Показано, что эффективное деление возможно при любой кратности в исследованном диапазоне, однако правильность формы получаемых колебаний с увеличением кратности деления и отклонением ее от целочисленных значений ухудшается.

Для интерпретации наблюдаемых явлений предложена гипотеза ударного возбуждения упругой подсистемы за счет связи с магнитной, происходящего за время релаксации магнитной подсистемы, при котором упругая система начинает колебаться с частотой собственного резонанса, что и наблюдается как деление частоты исходных колебаний. Отмечено, что такое ударное возбуждение упругой системы возможно только в сильно нелинейном режиме, когда амплитуда магнитных колебаний резко возрастает за незначительный промежуток времени, определяемый не столько временем релаксации магнитной системы, сколько крайне высокой амплитудой возбуждающего сигнала.

Для случая линейной поляризации возбуждающего поля на примере деления частоты на два выявлена роль нелинейности магнитной системы и отмечено, что процесс деления возможен в любой момент времени после начала возбуждения, в том числе по окончании релаксации обеих подсистем, то есть с процессами релаксации никак не связан. Рассмотрено деление исходной частоты в целочисленном и дробном отношении с коэффициентом кратности деления от 1 до 7. Показано, что для реализации такого непрерывного во времени процесса является необходимым сочетание двух условий: сильного нелинейного возбуждения и значительной величины константы магнитоупругого  взаимодействия, причем в зависимости от сочетания двух упомянутых условий характер магнитных колебаний значительно меняется.

Выявлены три основных режима магнитных колебаний.  

Режим №1 (определяемый возбуждением): основная частота магнитных колебаний равна частоте возбуждения, имеет место слабая примесь второй и третьей гармоник, параметрический портрет – правильный круг с одним или несколькими внутренними завитками.

Режим №2 (определяемый упругостью): основная частота магнитных колебаний равна частному от деления частоты возбуждения на коэффициент кратности деления и совпадает с частотой упругих колебаний, форма колебаний – прямоугольная или пилообразная с закругленными углами, параметрический портрет – круг с небольшими искажениями, обусловленными примесью высокочастотных гармоник.

Режим №3 (мультигармонический): частота основной составляющей магнитных колебаний совпадает с частотой упругих, форма основной составляющей колебаний близка к прямоугольным импульсам, на горизонтальных участках которых присутствуют колебания с частотой, почти на порядок превышающей частоту возбуждения. 

Выявлено, что колебания упругого смещения во всех этих режимах имеют правильную синусоидальную форму с частотой, определяемой толщиной пластины, то есть равной частному от деления частоты возбуждения на коэффициент кратности.

Показано, что решающим фактором в реализации того или иного режима, кроме достаточного уровня возбуждения, является величина константы магнитоупругого взаимодействия. Так при ее увеличении от минимума сначала возбуждается режим №1, затем режим №2, после чего режим №3. При дальнейшем увеличении этой константы наступает срыв колебаний системы в целом, представляющий собой экспоненциальное нарастание амплитуды магнитных колебаний, заканчивающееся укладыванием вектора намагниченности в плоскость пластины с соответствующим прекращением колебаний.

На основе исследования изменения константы магнитоупругости в широком диапазоне вплоть до значения, соответствующего переориентации, выявлен множественный перемежающийся характер чередования режимов, разделяемого чередующимися срывами, наступающий после первичного срыва, соответствующего минимальному необходимому для срыва значению константы магнитоупругости. Отмечено, что в этих условиях характер чередования режимов и срыва является нерегулярным. 

Для интерпретации явлений, наблюдаемых при линейной поляризации поля возбуждения, предложена гипотеза о двухрезонаторном характере системы, один из резонаторов которой – магнитный, является сильно нелинейным, тогда как другой – упругий, всегда остается чисто линейным. При сильно нелинейном возбуждении колебания магнитного резонатора обогащаются гармониками, тогда как упругий резонатор играет роль фильтра, выделяющего единственную частоту, соответствующую собственному резонансу. Высказано предположение, что наблюдаемый при высоком уровне линейно поляризованного возбуждения слегка флуктуирующий характер колебаний намагниченности, является основной причиной, ответственной за возможность реализации деления частоты в непрерывном режиме времени.

 

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

1. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.

2. Голямина И.П. Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М.: Наука. 1967.

3. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.

4. Ле-Кроу Р., Комсток Р. В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156. 

5. Bommel H.E., Dransfeld K. // Phys. Rev. Lett. 1959. V.3. № 2. P.83.

6. Spencer E.G., Denton R.T., Chambers R.P. // Phys. Rev. 1962. V.125. № 6. P.1950.

7. Eggers F.G., Strauss W. // J. Appl. Phys. 1963. V.34. № 4. Pt.2. P.1180.

8. Ферриты в нелинейных сверхвысокочастотных устройствах: Сб. статей: Пер. с англ. под ред. А.Г. Гуревича. М.: ИЛ. 1961. 

9. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209. (Перевод в [8].С.163.).

10. Моносов Я.А. Нелинейный ферромагнитный резонанс. М.: Наука. 1971.

11. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.

12. Шутый А.М., Семенцов Д.И. // ФТТ. 2000. Т.42. № 7. С.1268.

13. Шутый А.М., Семенцов Д.И. // ФТТ. 2001. Т.43. № 8. С.1439.

14. Шутый А.М., Семенцов Д.И. // ФТТ. 2002. Т.44. № 4. С.734.

15. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.

16. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. № 8. С.831. 

17. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000. Т.42. № 6. С.1062.

18. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Дисс. на соискание уч. степ. к.ф.-м.н. Москва. МГУ. 2007.

19. Карпачев С.Н., Власов В.С., Котов Л.Н. // Вестник МГУ. Сер.3. 2006. № 6. С.60.

20. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XVI Международной конференции "Радиолокация и радиосвязь". Москва-Фирсановка. Изд. МЭИ. 2008. С.197.

21. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

22. Власов В.С., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №5. С.482.

23. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М., Наука, 1978.

24. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Советское радио. 1964.

25. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь. 1986.

26. Харламов А.А. (ред.). Специальный физический практикум. Часть 1. М.: Изд.МГУ. 1977.  

27. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.139.

28. Власов В.С., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.153.

29. Власов В.С., Шавров В.Г., Щеглов В.И. // Материалы школы-конференции «XVI Международная зимняя школа-семинар по радиофизике и электронике сверхвысоких частот». Саратов: ООО «Издательский центр «Наука». 2015. С.32. 

30. Власов В.С., Шавров В.Г., Щеглов В.И. // Материалы школы-конференции «XVI Международная зимняя школа-семинар по радиофизике и электронике сверхвысоких частот». Саратов: ООО «Издательский центр «Наука». 2015. С.33. 

31. VlasovV.S., Kotov L.N., Shavrov V.G., Shcheglov V.I. // Book of Abstracts “20th International conference on magnetism”. Barcelona. 5-10 july 2015. P.872.  

32. Gilbert T.L. // IEEE Trans. on Magn. 2004. V.40. №6. P.3443.

33. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973..

34. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

35. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

36. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.