Методика оценивания вероятностных характеристик сигнально-кодовых конструкций с использованием турбо-подобных кодов и дискретных частотных сигналов в КВ канале.

Методика оценивания вероятностных характеристик сигнально-кодовых конструкций с использованием турбо-подобных кодов и дискретных частотных сигналов в КВ канале

И. В. Головкин

ФГОБУ ВПО МТУСИ

Статья получена 8 сентября 2015 г.

Аннотация. В работе предложена методика оценивания вероятностно-энергетических характеристик сигнально-кодовых конструкций (СКК) с использованием турбо-подобных кодов и дискретных частотных сигналов в упрощенной модели коротковолнового (КВ) канала.

Ключевые слова: дискретные частотные сигналы, КВ канал, турбо-подобные коды, аддитивная граница.

Abstract. The method for estimation bit error probabilities for serial concatenation of discrete frequency signals and turbo-like codes in simplified HF channel model is suggested in the paper. Results of computer simulation of discrete frequency signals with turbo-like code and theoretical estimation are presented.

Key words: discrete frequency signals, HF channel, turbo-like codes, additive bound.

Введение

Дискретные частотные сигналы (ДЧ) представляют собой последовательность радиоимпульсов, несущие частоты которых изменяются по определенному правилу [1]. Основным достоинством дискретных частотных сигналов как класса широкополосных сигналов является возможность получения достаточно высокой относительной скорости при ансамблях большого объема.

Радиоканалы КВ диапазона характеризуются многолучевым распространением радиоволн, высокой интенсивностью помех от других радиоэлектронных средств. В работе [2] приведены результаты проработки требований, предъявляемых к сигнально-кодовым конструкциям для КВ диапазона. Сигнально-кодовые конструкции с использованием дискретных частотных сигналов и соответствующих схем помехоустойчивого кодирования удовлетворяют требованиям, предъявляемым к сигналам первой группы (сигнально-кодовые конструкции, используемые для установления и ведения соединения со скоростями 50-250 бит/с).

В работе [3] рассмотрена СКК с использованием последовательного соединения турбо-подобных кодов и ДЧ сигналов. Целью данной работы является разработка методики оценивания вероятностно-энергетических характеристик конструкции, предложенной в работе [3].

1. Постановка задачи

Положим, так же как и в [1], что ДЧ сигнал состоит из элементов, а все элементы имеют одинаковую форму . Пусть номера элементов изменяются от 0 до , -комплексная амплитуда -го элемента -го ДЧ сигнала, а положение -го элемента по частоте определяется сдвигом, равным , где шаг разноса по частоте, - символ частотной кодовой последовательности, причем при изменении меняется в таких же пределах от 0 до M-1, но в определенном порядке. Длительность импульса равна , а его ширина спектра [1].

На рисунке Рис. 1а над каждым импульсом указана его несущая частота. На частотно-временной плоскости (см. рисунок Рис. 1б) штриховкой выделены квадраты, в которых распределена энергия импульсов ДЧ. Как видно из рисунка Рис. 1б, энергия ДЧ распределена неравномерно на частотно-временной плоскости.

Комплексная огибающая ДЧ сигнала [1]:

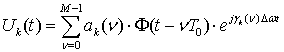
У рассматриваемых далее ДЧ сигналов первого порядка и форма имеет вид:

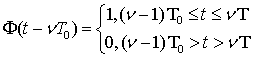
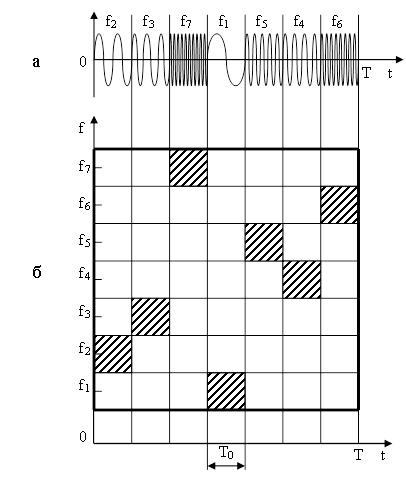
Рис. 1 а) Расположение импульсов на временной оси и
б) Расположение импульсов на частотно-временной плоскости

В качестве ансамбля дискретно частотных сигналов далее использована усеченная композиционная система ДЧ сигналов [4], сформированная по следующему правилу:

(1)

где обозначает -й элемент -й кодовой последовательности; и ; - номер элемента в сигнале. Объем системы при выбранном равен M-1 [4], варьируя , можно сформировать ансамбль объемом до .

На рис.2 приведена блок схема формирования исследуемой сигнально-кодовой конструкции.

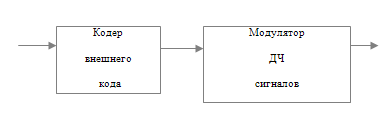
Рис. 2 Блок схема формирования исследуемой конструкции.

В качестве внешнего кода используется турбо-подобный код [5]. Ниже даны пояснения по блок-схеме кодера данного турбо-подобного кода, приведенной на рис.3.

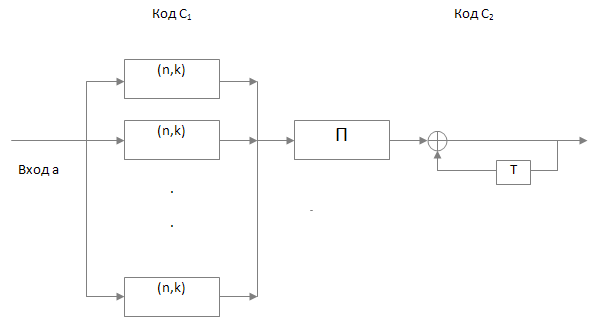
Рис. 3 Блок-схема формирования турбо-подобного кода

Внешний код включает идентичных блоковых кодов с порождающей матрицей . Здесь - длительность кодовых слов, - объем информационного блока.

В качестве внутреннего кода используется блоковый код , эквивалентный усеченному рекурсивному сверточному коду с кодовой скоростью 1 и длиной кодового ограничения 1 (число состояний кодовой решетки равно 2).

Длительность формируемых кодовых слов турбо-подобного кода равна , информационный объем равен , кодовая скорость равна .

Кодирование осуществляется следующим образом: последовательность информационных символов длительностью разбивается на групп одинаковой длительности , каждая из которых поступает на вход кодеров внешнего кода . Символы с выходов кодеров кода поступают на устройство перемежения П и далее на вход кодера внутреннего кода . В качестве кода будут рассматриваться совокупность биортогональных кодов, полученных на основе функций Уолша.

Закон перемежения кодовых символов внешнего кода , выполняемый перемежителем , определяет вероятностные характеристики турбо-кодов. Проблема выбора перемежителей рассматривалась в работе [6].

Последовательность символов кодовых слов турбо-подобного кода разбивается на последовательностей длительностью , поступающих на вход устройства формирования ДЧ сигналов, в качестве которых используется квазиоптимальная система ДЧ сигналов объемом .

Интервал корреляции замираний по спектру в КВ диапазоне волн обычно составляет 0,5 ÷ 2 кГц [7]. При разносе частот дискретных частотных сигналов на величину более интервала корреляций можно считать замирания по каждой из частот независимыми и имеющими рэлеевское распределение.

Особенностью рассматриваемых ДЧ сигналов является отсутствие повторений частот в сигнале. Упрощенная модель, с независимыми рэлеевскими замираниями по частотам, будет справедлива для рассматриваемых квазиоптимальных систем ДЧ сигналов при условии превышения величиной времени изменения параметров канала, обусловленной доплеровским расширением спектра.

Оценка вероятностных характеристик описанной конструкции при использовании указанной модели канала составляет суть рассматриваемой задачи.

2. Методика оценки вероятностных характеристик с использованием равновероятного перемежителя

Вследствие сложности вычисления точных значений вероятностных характеристик используют приближенные методы их оценивания, применяя верхние границы, например, аддитивную или мультипликативную границы [8-10].

Обозначим PEP (pairwise error event) вероятность того, что декодер выберет кодовое слово при условии, что передавалось в случае, когда возможны только два варианта решений: у декодера выбрать или выбрать . Предполагается, что при этом используется метод приема “в целом”. В общем случае вероятность зависит от способа отображения бит турбо-подобного кода в дискретные частотные сигналы, расстояния Хэмминга между кодовыми векторами турбо-подобного кода , корреляционных свойств ансамбля ДЧ сигналов :

В работе [11] предложено считать, что существует некоторый усредненный способ отображения бит турбо-подобного кода на дискретные частотные сигналы, при котором вероятность зависит от расстояния Хэмминга между векторами , а не от выбранной пары кодовых векторов.

Верхняя аддитивная граница имеет вид [11]

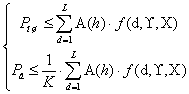
где - спектр расстояний Хэмминга турбо-подобного кода, -вероятность ошибки на кодовый блок, -вероятность битовой ошибки.

При использовании упрощенной модели КВ канала с независимыми рэлеевскими замираниями по частотам, сигнал воздействующий на вход приемника при передаче сигнала можно записать как:

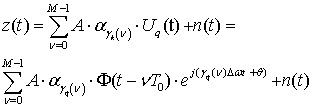
где комплексный коэффициент замирания на частоте , - амплитуда радиосигнала на входе приемного устройства, - начальная фаза радиосигнала, - комплексный шум с квадратурными компонентами имеющими нормальную плотность распределения и дисперсиями , - односторонняя спектральная плотность мощности.

При неизвестных коэффициентах замираний, неизвестных относительных задержках и неизвестных фазах лучей в каналах с многолучевым распространением используется правило некогерентного приема [12,13] c некогерентным накоплением. Элементы ДЧ сигнала обрабатываются некогерентно

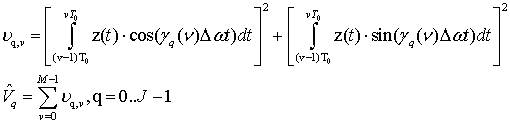(2)

где -объем ансамбля ДЧ сигналов.

Комплексные коэффициенты замираний на частотах имеют независимые квадратурные составляющие с нормальным распределением и с нулевым средним, компоненты шума также имеют нулевое среднее.

Поэтому величина

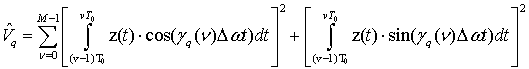
имеет центральное хи-квадрат распределение с степенями свободы [14,15]:

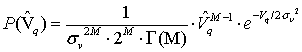
где -гамма функция, -дисперсия гауссовских величин, образующих .

Дисперсия квадратурных компонент, в случае если передавался сигнал ,

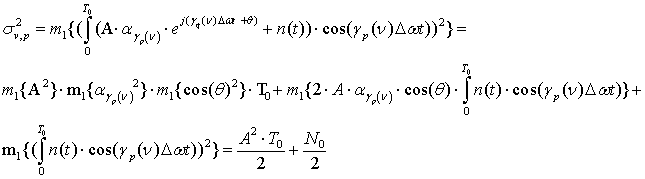
где -операция математического усреднения.

В случае отсутствия сигнала, дисперсия квадратурных составляющих

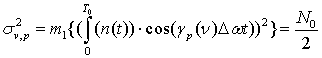
Вероятность правильного приема есть вероятность при условии что передавался сигнал .

Тогда вероятность ошибки может быть записана как [17]

(3)

Предположим, что построена такая система ДЧ сигналов, где все сигналы ортогональны. Тогда выражение (3) может быть записано:

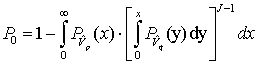
Рассмотрим интеграл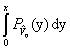

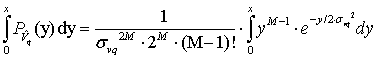
Значение определенного интеграла 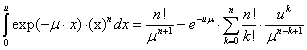приведено в [16] , таким образом

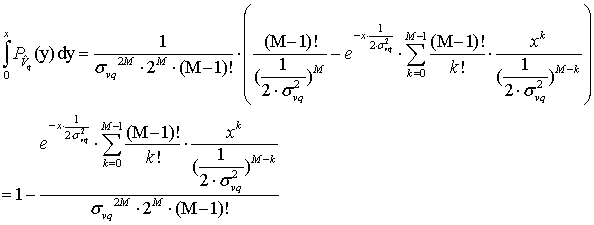
Вероятность ошибки может быть записана как

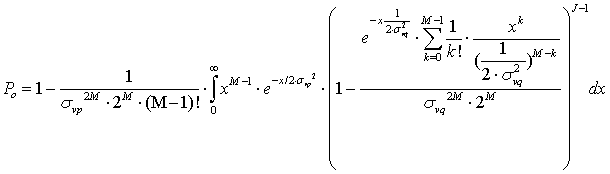(4)

Интеграл в формуле (4) может быть вычислен численными методами.

У каждого из ДЧ сигналов, получаемых по формуле (1) имеется ровно одна частотная позиция общая с любым другим ДЧ сигналом из данного ансамбля. Воспользуемся методикой, предложенной в книге [17]. Предположим, что синтезирован ансамбль ДЧ сигналов, у которого временных позиций различны по частоте для всех сигналов, а последняя позиция одинакова. Тогда вероятность ошибки в точности равна вероятности ошибки при передаче ортогональной совокупности содержащей первые временных позиций. Таким образом формула (4) может быть использована для оценки вероятности ошибки равноудаленных ДЧ сигналов при подстановке при вычислениях вместо величины , величины .

Спектр расстояний Хэмминга турбо-подобного кода может быть получен с использованием равновероятного перемежителя [8,10].

Введем в рассмотрение многочлен (IOWEF) [10] от переменных для блокового кода с параметрами (), здесь - количество кодовых слов с весом Хэмминга анализируемого кода с весом информационной последовательности . Равновероятный перемежитель осуществляет отображение последовательности кодовых символов внешнего кода длительностью и весом во все возможные последовательности на входе внутреннего кода турбо-кода с равными вероятностями .

Для последовательного соединения турбо-кодов на основе составляющих блоковых кодов () и () справедливо соотношение относительно [10]

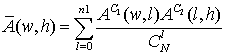
Усредненный спектр расстояний Хэмминга кода полученного на основе последовательного соединения кодов равен

В качестве кода в рассматриваемой схеме выступают биортогональных кодов, полученных на основе функций Уолша . Так как объем информационной части используемых биортогональных кодов невелик 4..10 бит , многочлен для них может быть получен компьютерным перебором.

Многочлен объединения кодов определяется по формуле [8]

Многочлен для усеченного рекурсивного сверточного кода с кодовой скоростью 1 и длиной кодового ограничения 1 определяется формулой [18]:

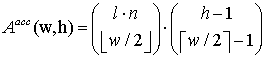
Усредненный спектр для турбо-подобного кода, полученного на основе биортогональных сигналов с параметрами приведен на рис. 4.

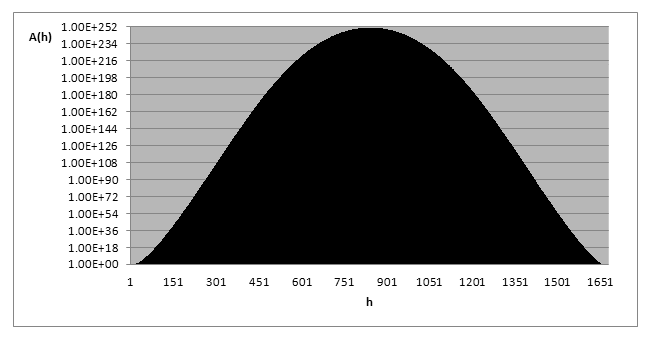
Рис.4. Усредненный спектр весов Хэмминга для турбо-подобного кода n=1680, k=840 полученного на основе биортогональных сигналов n=8, k=4.

Вероятность зависит от распределения ошибочных бит при отображении на дискретные частотные сигналы. В работе [19] предложено выполнять усреднение по всем возможным способам отображения ненулевых бит в символы используемой модуляции c использованием равновероятного перемежителя расположенного перед устройством отображения бит в дискретные частотные сигналы. При этом аддитивная граница может быть записана как

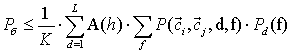(5)

Где вероятность появления именно этой комбинации отображения ненулевых бит на символы. Вероятность определяется формулой [19]:

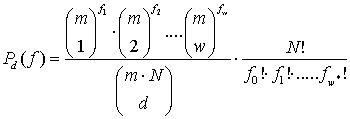
где число бит переносимых одним ДЧ сигналом, общее число ДЧ сигналов в кодовом блоке, , вес Хэмминга бит переносимых ДЧ сигналом в данной комбинации отображения ненулевых бит .

Аддитивная граница имеет хорошую точность при больших отношениях сигнал шум, при этом основной вклад вносят члены с минимальными весами Хэмминга в формуле (5).

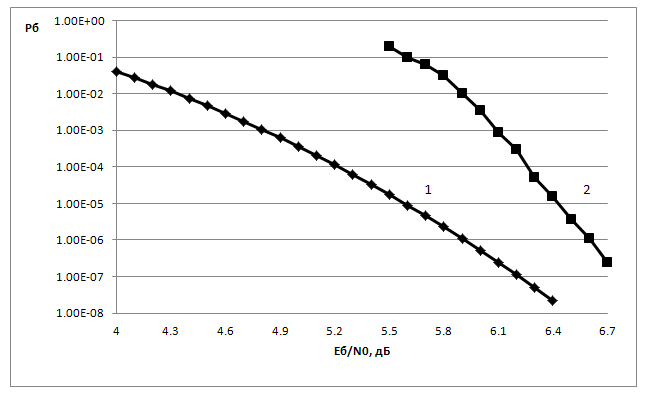
Рис.5 Вероятностные характеристики для турбо-подобного кода n=1680, k=840 полученного на основе биортогональных сигналов n=8, k=4, ансамбль ДЧ сигналов с , : 1 - использование усредненного множества и аддитивной границы; 2 – экспериментальная кривая.

Из рис.5 видно, что при использовании усредненного множества и аддитивной границы теоретическая кривая (кривая 1) для рассматриваемого турбо-подобного кода близка к экспериментальной кривой (кривая 2). При расчете теоретической кривой использовались члены с весами Хэмминга не более 30. Экспериментальная кривая получена при использовании алгоритма итеративной демодуляции декодирования описанного в [3,20], количество итераций 50. Можно заключить, что для анализируемых значений сигнал/помеха энергетические потери при использовании алгоритма итеративного приема рассматриваемых турбо-подобных кодов достигают значений до 0.6 дБ по отношению к оптимальному приему, реализующему правило максимального правдоподобия.

Заключение

1. Разработана методика теоретического оценивания вероятностных характеристик при приеме сигнально-кодовых конструкций с использованием турбо-подобных кодов и ДЧ сигналов для упрощенной модели КВ канала. В качестве вероятностной характеристики принята вероятность ошибки на бит при использовании метода приема “в целом”.

2. Основу разработанной методики оценки составляет аддитивная граница. При этом используется усредненный спектр весов Хэмминга для турбо-подобного кода.

3. Выполнена апробация приведенной методики при исследовании вероятностных характеристик для турбо-подобного кода. Показано соответствие теоретических и экспериментальных вероятностных кривых.

4. Разработанная методика может быть применена для теоретического оценивания вероятностных характеристик общего класса сигнально-кодовых конструкций с использованием последовательного соединения ДЧ сигналов и схем помехоустойчивого кодирования.

Литература

1. Варакин Л.Е. Системы связи с шумоподобными сигналами, – М.: Радио и связь, 1985,384с.

2. Маковий В.А. Построение современных систем радиосвязи КВ диапазона. // Теория и техника радиосвязи. – 2009. – № 3. – С. 76–86.

3. Головкин И.В. Сравнительный анализ помехоустойчивых кодов для систем с использованием дискретных частотных сигналов и итеративной обработкой в каналах с замираниями. // Труды 69-й Научной сессии, посвященной Дню Радио. 21-23 мая 2014.

4. Варакин Л. Е. Теория систем сигналов. — М.: Сов. радио, 1978. 304 с.

5. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема.// Радиотехника и электроника. - 2010. - Т. 55, N 10. - С. 1193-1199.

6. Giulietti A., Perre L., Strum M. Parallel turbo coding interleavers: avoiding collisions in accesses to storage elements.// Electronics Letters. 2002. V.38. N5. P. 232-234.

7. Васильев К.К., Глушков В.А., Дормидонтов В.А., Нестеренко А.Г.;под общ. ред. К.К. Васильева. Теория электрической связи: учебное пособие . – Ульяновск: УлГТУ, 2008. – 452 с.

8. Benedetto S., Montorsi G. Unveiling turbo-codes: some results on parallel concatenated coding schemes.// IEEE Trans. Inform. Theory. 1996. V.42. №2. P.409-429.

9. Смольянинов В.М., Назаров Л.Е. Мультипликативная граница вероятности правильного распознавания при когерентном приеме.// Радиотехника и электроника. 1987. Том 32. №2. Стр. 446-449.

10. Benedetto S., Divsalar D., Montorsi G., Pollara F. Serial concatenation of interleaved codes: performance analysis, design, and iterative decoding.// IEEE Trans. on Inform. Theory. 1998. V.44. N3. P.909-926.

11. G. Caire, G. Taricco, and E. Biglieri, Bit-interleaved coded modulation, IEEE Trans. Inf. Theory, vol. 44, no. 3, pp. 927-946, 2 1998.

12. Мазурков М. И. Системы широкополосной радиосвязи: учебное пособие для студентов высших учебных заведений / М. И. Мазурков. — Одесса : Наука и техника, 2010. — 340 с.

13. Финк Л.М. Теория передачи дискретных сообщений. – М.: Советское радио, 1970. – 728с.

14. Прокис Дж. Цифровая связь: Пер. с англ. - М.: Радио и связь, 2000. - 800 с.

15. Marvin K. Simon, Probability Distributions Involving Gaussian Random Variables: A Handbook for Engineers, Scientists and Mathematicians, Springer-Verlag New York, Inc., Secaucus, NJ, 2006

16. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М: Гос. изд-во физ.-мат. литературы. 1963. 1100 с.

17. Витерби Э.Д. Принципы когерентной связи. Перевод с англ. ‑ М.: Сов. Радио.‑ 1970.‑ 392 с.

18. D. Divsalar, H. Jin and R. J. McEliece, “Coding theorems for ‘turbo-like’ codes,” in Proc.36th Allerton Conf. on Communications, Control and Computing, Allerton, IL, pp. 201–210,1998.

19. P. Yeh, S. Zummo, and W. Stark, “Error probability of bit-interleaved coded modulation in wireless environments,” IEEE Transactions on Vehicular Technology, vol. 55, no. 2, pp. 722–728, 2006.

20. Головкин И.В., Маныкин Д.Н., Елсуков Б.А., Клоков С.С. Сигнально кодовая конструкция с использованием ортогональных сигналов и турбо-подобных кодов для некогерентного приема. // T-comm – Телекоммуникации и транспорт. – 2014. – №10. – С. 15-20.