УДК 621.385.632
О ТРАНСПОРТИРОВКЕ ЛЕНТОЧНОГО ЭЛЕКТРОННОГО ПУЧКА
В АКСИАЛЬНО-СИММЕТРИЧНОМ МАГНИТНОМ ПОЛЕ
В.
Л.
Саввин1, А. В. Коннов2, Д.
А. Михеев1, Г. М.
Казарян1, И. И. Шуваев1
1Физический факультет МГУ имени М.В. Ломоносова,
2ФГУП «НПО ТОРИЙ»
Статья получена 10 сентября 2015 г.
Аннотация. С помощью компьютерного моделирования с использованием 3D-модели ленточного электронного пучка проведен траекторный анализ при транспортировке пучка в стационарном магнитном поле при наличии циклотронного вращения пучка, определены области стабильности пучка и выявлены условия возбуждения диокотронной неустойчивости.
Ключевые слова: ленточный электронный пучок, циклотронное вращение, диокотронная неустойчивость.
Abstract. Trajectory analysis of sheet electron beam transportation was conducted in stationary magnetic field at presence of cyclotron rotation, the areas of stability of the beam were defined and the terms of excitation of diocotron instability were educed by means of computer design using 3d-model of sheet electron beam.
Keywords: sheet electron beam, cyclotron rotation, diocotron instability.
Введение
Микроволновые устройства с ленточными электронными потоками могут обладать очевидными преимуществами по сравнению с СВЧ-устройствами с цилиндрическими электронными пучками. Ленточные пучки с широким прямоугольным (или эллипсоидальным) сечением дают возможность реализовать одновременно большой ток пучка и низкую плотность пространственного заряда [1], снизить уровень фокусирующего магнитного поля и обеспечить высокую эффективность СВЧ устройств с широкой полосой частот, высокими значениями импульсной и средней мощности. Исследования последних лет наглядно продемонстрировали перспективы микроволновых устройств с ленточными электронными потоками в миллиметровом и терагерцовом диапазонах [2-8]. Ленточные пучки с циклотронным вращением электронов перспективны и для поперечно-волновых СВЧ устройств [9-10].
Изучение динамики ленточного электронного пучка в области формирования потока и в рабочем канале электродинамических систем является первоочередной задачей для создания отечественных мощных микроволновых устройств миллиметрового диапазона. Влияние пространственного заряда и проводящих поверхностей рабочего канала, периодический характер магнитных фокусирующих систем, деформация формы поперечного сечения и пульсации электронного потока, приводящие к спонтанному экспоненциальному росту флуктуаций плотности пространственного заряда, возбуждение диокотронной неустойчивости ленточного пучка – одни из факторов, требующих детальных исследований с применением трехмерного компьютерного моделирования.
Транспортировка ленточного электронного пучка в аксиально симметричном магнитном поле в канале дрейфа имеет ряд отличительных особенностей. Действие компоненты Ey поля пространственного заряда в ленточном электронном пучке, распространяющемся параллельно осевому однородному магнитному полю B, вызывает сдвиг между верхней и нижней половинами сечения пучка (Рис. 1).
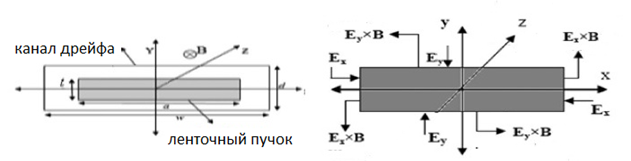
Рис.1 Ленточный
пучок в канале дрейфа (слева) и сечение пучка (справа),
Еx
и Ey – компоненты
электрического поля пространственного заряда пучка, B
– внешнее магнитное поле
Сдвиг и пульсации сечения потока может также привести к спонтанному экспоненциальному росту флуктуаций плотности пространственного заряда и возмущений в потоке, т.е. к возбуждению диокотронной неустойчивости. Заметная деформация формы поперечного сечения может возникнуть под влиянием Ex–компоненты поля пространственного заряда, резко нарастающей к краям поперечного сечения пучка:
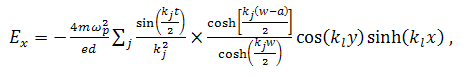 (1)
(1)
где ![]() – плазменная частота, размеры
пучка и канала дрейфа указаны на рис.1.
– плазменная частота, размеры
пучка и канала дрейфа указаны на рис.1.
Рост Ex–компоненты поля пространственного заряда при приближении к краям поперечного сечения ленточного пучка иллюстрирует рис.2.
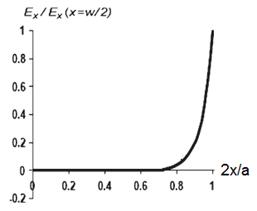
Рис.2 Изменение Ex–компоненты поля пространственного заряда при приближении к краям поперечного сечения ленточного пучка
Численная 3D – модель ленточного пучка
Для анализа устойчивости ленточного пучка разработана численная 3D - модель, содержащая фрагмент протяженного в продольном направлении электронного потока с периодическими по оси z граничными условиями. Модель пучка включает нечетное количество периодов инжекции пучка Ni, т.е. Ni =1, 3 , 5, ... В этом случае параметры взаимодействия определяются по “cредней” группе инжектированных электронов, принадлежащих (Ni + 1)/2 периоду. Все остальные частицы являются буферными. В процессе расчетов устойчивости ленточного пучка использовалось 1 – 5 периодов. На рис.3 слева показано поперечное сечение модели ленточного пучка (частицы в сечении «расчетного» периода в текущий момент времени), справа - конфигурация буферных и расчетного (синий) периодов модели в текущий момент времени (видно четыре периода инжекции, вверху – вид сбоку, внизу – вид сверху).

Рис.3 Численная 3D - модель ленточного пучка
Движение частиц модели описывается уравнениями
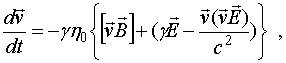 (2)
(2)
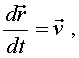 (3)
(3)
здесь
![]() и
и ![]() –
радиус-вектор и скорость отдельной частицы, t – текущее время,
–
радиус-вектор и скорость отдельной частицы, t – текущее время, 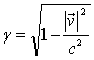 , c–
скорость света,
, c–
скорость света, 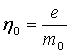 – удельный заряд электрона,
– удельный заряд электрона, ![]() = {Bx(x,y,z),
By(x,y,z), Bz(z)} – магнитное поле в
области, электрическое поле
= {Bx(x,y,z),
By(x,y,z), Bz(z)} – магнитное поле в
области, электрическое поле ![]() , где
, где ![]() – внешнее электрическое поле,
– внешнее электрическое поле, ![]() = {Eqx(x,y,z),
Eqy(x,y,z) ,Eqz(x,y,z)} –
поле пространственного заряда.
= {Eqx(x,y,z),
Eqy(x,y,z) ,Eqz(x,y,z)} –
поле пространственного заряда.
Поперечное сечение ленточного пучка разбивается на Nx·Ny крупных частиц с дискретностью по фазам влета Nz. Таким образом, в области взаимодействия может находиться одновременно Ni·Nx·Ny·Nz крупных частиц.
Крупная частица в трехмерной модели пучка представляет собой бесконечную последовательность частиц (субчастиц) шарообразной формы с равномерно распределенной плотностью пространственного заряда, имеющих всегда одинаковые поперечные координаты (x,y) и расположенных на одной прямой, параллельной оси z, на расстоянии Ni·Li, где Li – длина цуга инжектированных за период частиц. В частности, Li = lc. Cубчастица, принадлежащая “среднему” периоду инжекции, является базовой по отношению к остальным субчастицам. Все субчастицы, входящие в одну крупную частицу, двигаются синхронно. Поле пространственного заряда, создаваемое одной i-ой крупной частицей, записывается в виде суперпозиции полей составляющих ее субчастиц.
Результаты численного моделирования
Целью проводимых исследований являлся анализ устойчивости ленточного пучка во внешнем магнитном поле. Численные параметры модели ленточного пучка - потенциал пучка U0– в пределах 2-10 кВ, сечение пучка – до 1х20 мм, значения микропервеанса – 1-20 мкАВ-3/2 , величина внешнего фокусирующего магнитного поля - 0,0875 Тл, что обеспечивает циклотронный резонанс на частоте 2,45 ГГц. Отметим, что для выбранных параметров модели отношение микропервеанса пучка к площади его поперечного сечения достигало значений 1 мкАВ-3/2 /мм2.
На первом этапе рассчитывалась транспортировка пучка в отсутствие циклотронного вращения частиц. В случае однородного внешнего фокусирующего магнитного поля и сечения пучка 1х10мм электронный пучок практически сохраняет форму своего поперечного сечения при токе пучка, соответствующем значениям микропервеанса 1 мкАВ-3/2 (рис.4).
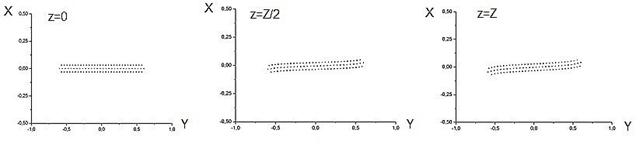
Рис.4 Поперечные сечения ленточного
пучка с микропервеансом 1 мкАВ-3/2
в начале (z=0),
в середине (z=Z/2)
и в конце области (z=Z)
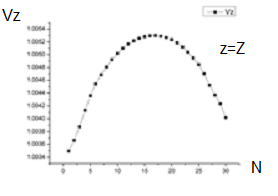
Рис.5 Изменение
продольной скорости ![]() частиц вдоль
ширины пучка
частиц вдоль
ширины пучка
Изменение продольной скорости частиц при этом значении микропервеанса – незначительно (рис.5). Увеличение микропервеанса до значения 4 мкАВ-3/2 незначительно изменяет форму поперечного сечения пучка (рис.6).
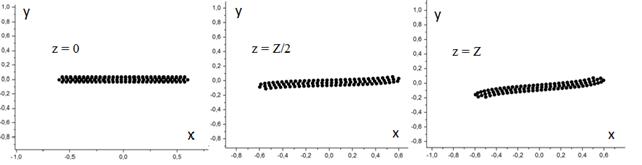
Рис.6
Поперечные сечения ленточного пучка с микропервеансом 4 мкАВ-3/2
в
начале (z=0), в середине (z=Z/2) и в конце области
(z=Z)
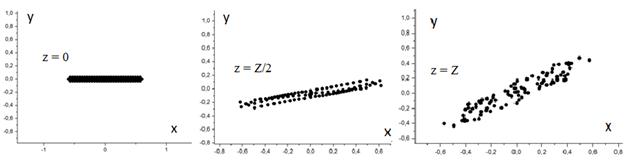
Рис.7
Поперечные сечения ленточного пучка с микропервеансом 20 мкАВ-3/2
в
начале (z=0), в середине (z=Z/2) и в конце области
(z=Z)
Дальнейшее увеличение тока пучка I0 (до значения микропервеанса 10-20) может приводить к заметным искажениям формы поперечного сечения, пульсациям внешних размеров сечения и возбуждению диокотронной неустойчивости (рис.7)
Этого удается избежать при задании равновесной толщины пучка и увеличении ширины пучка вдвое – для конкретного варианта поперечного сечения 1х20 мм (рис.8).
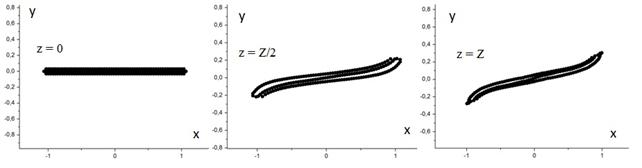
Рис.8 Сечения ленточного пучка 1x20мм с микропервеансом 20
В случае пучка с циклотронным вращением частиц (мощность циклотронного вращения пучка вдвое превышает мощность его продольного движения P0= I0∙U0) устойчивость ленточного пучка может быть более стабильной в случае расширяющегося магнитного поля (см. рис.9), хотя при этом площадь поперечного сечения пучка увеличивается.
Для приведенного примера размер сечения пучка в начале области с расширяющимся магнитным полем - 1х10мм, ток I0= 1,79А, U0 =2000В, циклотронный радиус Rc=2,44мм, первеанс – 10∙10-6 А/В3/2. В конце области индукция магнитного поля уменьшается в 10 раз.
Это достигается благодаря уменьшению фактора E×B, ответственного за деформацию поперечного сечения ленточного пучка. Во-первых, за счет увеличения площади сечения пучка в расширяющемся магнитном поле уменьшается поле пространственного заряда E.
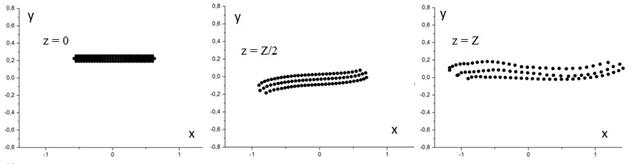
Рис.9 Поперечные сечения ленточного пучка с циклотронным вращением в области в расширяющемся магнитном полем
Во-вторых, за счет уменьшения фокусирующего магнитного поля B (в 5-10 раз на длине области). Отмеченный эффект может быть полезен при разработке практических конструкций СВЧ-устройств с циклотронными волнами.
Выводы
В случае однородного внешнего фокусирующего магнитного поля электронный пучок практически сохраняет форму своего поперечного сечения при токе пучка, соответствующем значениям микропервеанса pμ=1 - 5.
Дальнейшее увеличение тока пучка (pμ=10 - 20) может приводить к заметным искажениям формы поперечного сечения, пульсациям внешних размеров сечения и возбуждению диокотронной неустойчивости.
В случае циклотронного вращения частиц в расширяющемся магнитном поле устойчивость ленточного пучка может быть более стабильной.
Отмеченный эффект может быть полезен при разработке практических конструкций СВЧ-устройств с циклотронными волнами.
Литература
1. И.В. Алямовский. Электронные пучки и электронные пушки. М. Сов.Радио. 1966.
2. J. Pasour et al. Solenoidal Transport of Low-Voltage Sheet Beams for Millimeter Wave Amplifier // Proc. IVEC, Monterey. P.179-180. 2009.
3. K.T. Nguyen et al. Intense Sheet Electron Beam Transport in a Uniform Solenoidal Magnetic Field // IEEE Trans. Electron Devices. V.56. No.5. P. 744-751. 2009.
4. J. Pasour et al. Demonstration of a 100-kW Solenoidally Focused Sheet Electron Beam for Millimeter-Wave Amplifiers // IEEE Trans. Electron Devices. V.58. No.6. P.1792-1797. 2011.
5. P. Ch. Panda, V. Srivastava, A. Vohra. Analysis of Sheet Electron Beam Transport Under Uniform Magnetic Field // IEEE Trans. Plasma Science. V.41. No.3. P. 461-468. 2013.
6. J. Pasour et al. Demonstration of a Multikilowatt, Solenoidally Focused Sheet Beam Amplifier at 94 GHz // IEEE Trans. Electron Devices. V.61. No.6. P. 1630-1636. 2014.
7. D. Pershing et al. Demonstration of a Wideband 10-kW Ka-Band Sheet Beam TWT Amplifier // IEEE Trans. Electron Devices. V.61. No.6. P. 1637-1642. 2014.
8. C. Ruan et al. Theoretical and Experimental Investigation on Intense Sheet Electron Beam Transport With Its Diocotron Instability in a Uniform Magnetic Field // IEEE Trans. Electron Devices. V.61. No.6. P. 1643-1650. 2014.
9. В.Л. Саввин и др. О динамике ленточного электронного пучка в плоско-симметричном реверсе магнитного поля // // Известия РАН. Серия физическая, том 77, №12, С.1785-1788, 2013.
10. D. Mikheev, V. Savvin, G. Kazaryan, et al. Dynamics of sheet electron beam in cyclotron-wave converter // Proc.Vacuum Electron Sources Conference (IVESC), Saint-Petersburg, p.1, 2014.