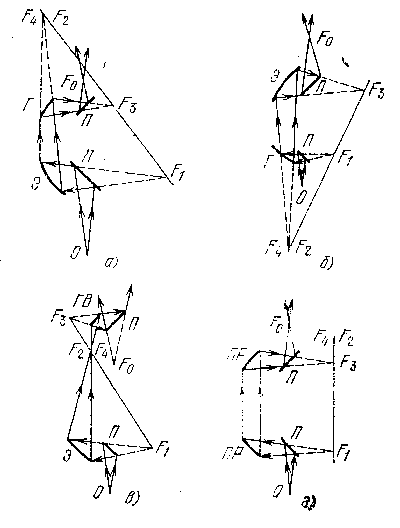Влияние различия диаграмм направленности осесимметричной
антенны в двух ортогональных плоскостях по амплитуде и фазе на
уровень кроссполяризации.
иллюстрирует влияние амплитудных и фазовых
соотношений диаграмм направленности осесимметричной антенны в Е-
и Н- плоскостях, определяемое формулой (7), на
уровень кроссполяризации.
Разложение векторной диаграммы направленности произвольной
антенны на компоненты правой и левой (1), или двух
линейных (3) поляризаций имеет смысл в
фиксированной сферической системе координат, заданной положением
своей полярной оси. Естесственно желание получить ответы на
следующие вопросы: как меняются поляризационные соотношения при
преобразованиях системы координат, при каких преобразованиях
антенна остаётся идеально поляризованной?
Рассмотрим случай поворота оси сферической
системы координат (наклона антенны). Этот случай
важен при расчете кроссполяризации несимметричных зеркальных
антенн. Получим формулы преобразования компонент разложения
(1), (3) при повороте оси сферической
системы координат на угол q0. Сначала обратимся к
частному случаю, когда поворот происходит вокруг совпадающих осей
OY и OYў.
На рис.
4
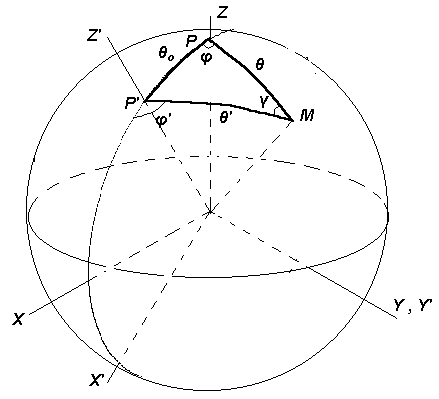 Рис4
.
Рис4
. Сферический треугольник.
изображён
сферический треугольник PўMP, образованный дугой
q0, соединяющей полюсы систем координат, и
меридиональными дугами q и qў -
соответствующими сферическим координатам {q, f} и
{qў, fў} некоторой точки M на сфере
в двух рассматриваемых системах координат. Вместе с разложением
(1) можно выписать аналогичное разложение в
штрихованной системе координат:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
|
ж
з
з
з
з
и
|
|
| |
ц
ч
ч
ч
ч
ш
|
|
| (8) |
Компоненты [^F]r, [^F]l описывают диаграммы
направленности антенны по круговым поляризациям правого и левого
вращения в новой (штрихованной) системе координат.
Если обозначить g угол между дугами q и
qў в точке M, сферические компоненты вектора
E будут связаны преобразованием:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
|
| (9) |
Применяя последовательно преобразования (2),
(9) и (8), найдем требуемую связь:
|
Fr(q,f) = ei d |
^
F
|
r
|
(qў,fў), Fl(q,f) = e-i d |
^
F
|
l
|
(qў,fў) |
| (10) |
Фазовое искажение d диаграмм направленности
круговой поляризации совпадает с точностью до знака с угловым
избытком e сферического треугольника PўMP,
определяемым по формуле:
Знак фазы положительный для той составляющей,
направление вращения которой совпадает с направлением обхода
тройки лучей: текущего и лучей, направленных вдоль старой и
новой полярных осей.
Связь между поляризационной характеристикой зеркальной антенны
и понятием углового избытка сферического треугольника
была замечена Вудом [3] при анализе эффектов
кроссполяризации параболической зеркальной антенны с вынесенным
фокусом. Из геометрии известно [11] что, сумма
внутренних углов сферического треугольника превышает
180°, если длины его сторон не больше 180°,
превышение численно равно площади треугольника для сферы
единичного радиуса. Угловой избыток сферического треугольника
PўMP можно вычислить по двум сторонам треугольника и
углу между ними по формуле [11]:
|
|
ctg
| (e/2) = |
ctg
| (q0/2) |
ctg
| (q/2) |
cosec
| f+ |
ctg
| f. |
| (11) |
Поскольку в
плоскости поворота системы координат сферический треугольник
PўMP на рис.
4
вырождается в отрезок прямой линии и
имеет нулевую площадь, угловой избыток обращается в нуль, и
кроссполяризация отсутствует. При переходе через плоскость
поворота фазовая ошибка d меняет знак из-за изменения
направления отсчёта углов в треугольнике.
Произвольный поворот оси сферической системы координат на угол
q0 задаётся тремя углами Эйлера { f0, q0,fў0 }, причём f0 и fў0 - это азимутальные
координаты оси поворота полярной оси в плоскостях XOY и
X'OY', соответственно.
Фазовые искажения составляющих
круговой поляризации по формуле (10) в общем случае
определяются выражением:
Итак, при повороте оси сферической системы координат компоненты
круговой поляризации векторной диаграммы направленности
искажаются, согласно (10), но только по фазе. Антенна
идеальной круговой поляризации остается при этом идеально
поляризованной. Из-за того что фазовые искажения круговых
поляризаций правого и левого вращений имеют различные знаки, в
базисе линейных поляризаций при повороте оси системы
координат возникает кроссполяризация. Используя преобразования
(5) и (10) можно получить связь компонент
линейной поляризации диаграммы направленности в двух сферических
системах координат со взаимно повернутыми осями:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
|
ж
з
з
з
з
и
|
|
| |
ц
ч
ч
ч
ч
ш
|
|
| (13) |
Данное соотношение показывает, что компоненты линейной
поляризации при повороте полярной оси сферической системы
координат поворачиваются на угол d, связанный с угловым
избытком сферического треугольника, образованного дугой поворота
полярной оси и дугами, соединяющими точку наблюдения с полюсами
(старым и новым) системы координат.
4 Источники кроссполяризованного
излучения
4.1 Разделение источников излучения в базисе круговых
поляризаций
В данном разделе исследуется вопрос о возможности
выделения источников кроссполяризованного излучения. Наиболее
полный анализ поляризационной структуры излучения антенн может
быть произведён в базисе круговых поляризаций, причём анализ не
зависит от выбора системы координат. Следуя [12],
сделаем следующее преобразование векторов поля в уравнениях
Максвелла:
|
F+ = 0.5(E - i[m0/e0]1/2 H), F- = 0.5(E + i[m0/e0]1/2 H) |
| (14) |
Уравнения Максвелла
при этом,
диагонализируются:
Если ввести обозначения:
|
| |
|
|
|
w[m0 e0]1/2, z0 = [m0/e0] 1/2, |
| |
|
| |
|
| (17) |
| |
|
преобразованные уравнения Максвелла примут
следующий вид:
|
rot F+ - k F+ = + |
1
k
|
j+, rot F- + k F- = - |
1
k
|
j- |
| (18) |
то есть, система уравнений
относительно векторов поля E,H сводится к двум
независимым уравнениям относительно векторов
F+, F-,
причём, источники поля в правой части уравнений также независимы,
преобразованные векторы поля
F+, F- возбуждаются и
распространяются независимо друг от друга. Каждый вектор поля
F+, F- удовлетворяет векторному
дифференциальному уравнению первого порядка.
Покажем, что источники j+ возбуждают в дальней зоне волну
идеальной правой круговой поляризации по всем
направлениям, а источники j- - волну идеальной левой
круговой поляризации. Направим ось Z по направлению
электрического и магнитного диполей с плотностями электрического
и магнитного тока je и jm, а оси X
и Y так, чтобы ортогональная система координат {X,Y,Z}
образовывала бы правую тройку.
В сферической системе координат, связанной с тройкой X,Y,Z
поле дальней зоны электрического и магнитного диполей описывается
выражениями [13] :
|
| |
|
|
|
|
|
(i k z0 e-i k r/2 r) sinqjze ; |
| |
|
|
|
| - (i k e-ik r/2 r) sinqjzm |
|
| |
| (19) |
Если jm = i z0je то j- = 0; в этом случае
F- = 0 и F+ = E . Из формул (19) следует,
что если временная
зависимость описывается множителем ei wt , то вектор
E вращается по часовой стрелке вдоль направления
распространения радиоволн, а это означает, что поле в дальней
зоне имеет идеальную правую круговую поляризацию.
Аналогично, в случае jm = - iz0 je , j+ = F+ = 0, F- = E, вектор вращается против
часовой стрелки при движении вдоль направления распространения
волны, и поле имеет идеальную левую круговую поляризацию.
Сумма двух полей, имеющих в дальней зоне идеальную круговую
поляризацию одного направления вращения, в
дальней зоне также поляризована по кругу и имеет то же направление
вращения. То же относится к сумме полей, возбуждённых
произвольной совокупностью источников поля круговой поляризации
одного направления вращения.
Задачи возбуждения электромагнитного поля, выраженного через
векторы поля F+, F-,
с учётом условий излучения при
r ® Ґ принимают следующий вид:
|
| |
|
| |
| (F- ,rort) = O(|r-2 |), r ® Ґ |
|
| |
| (20) |
rort - единичный
радиальный вектор , (*,*) - скалярное произведение.
Вопросы корректной постановки краевых задач для уравнений вида
|
rot F + k F = 0, rot F - k F = 0 |
|
рассмотрены в работе [14].
В этой работе показано, что для корректной постановки краевой
задачи в качестве граничных условий на поверхности можно задавать
какую-нибудь одну поверхностную компоненту вектора F.
В терминах
векторов F+, F-
могут быть выражены все физические
соотношения электромагнитного поля, в частности, выражение для
вектора Умова-Пойнтинга примет следующий вид:
|
P = |
1
2 z0
|
Jm([F+,F+*] -[F-,F-*]) |
| (21) |
(верхний индекс в виде * обозначает комплексное сопряжение)
Итак, в свободном пространстве общее
электромагнитное поле может быть однозначно разложено на
компоненты правой и левой круговых поляризаций. Если источники
одной из круговых поляризаций отсутствуют, антенна излучает поле
идеальной круговой поляризации одного направления вращения.
Кроссполяризационная составляющая антенны круговой
поляризации определяется только источниками ортогональной
поляризации. Удобство описанного представления электромагнитного
поля обусловлено независимостью возбуждения и распространения
компонент круговой поляризации в однородном пространстве, которая
позволяет разделить источники кроссполяризации. Из этого следует,
что кроссполяризация может возникнуть из-за неидеальности самих
источников возбуждения поля, при нарушении материальной
однородности пространства, но не может возникать при
распространении радиоволн в свободном пространстве, например,
из-за лучевых особенностей поля (фокусов, каустик, границ света и
тени).
С помощью теоремы
эквивалентности поле излучения зеркальной антенны
может быть представлено в виде интеграла от распределения
электрических и магнитных токов по плоскости апертуры. Такое
представление для диаграммы направленности апертурных
антенн используется чаще всего, хотя апертурное распределение
электрических и магнитных токов не может быть задано произвольным
образом, а определяется как условиями облучения зеркала, так и
условиями краевой дифракции и затекания токов на обратную сторону
зеркал. Преобразуем поле излучения апертурной антенны в дальней
зоне к виду, удобному для поляризационного анализа в базисе
круговых поляризаций. Пусть ось сферической системы координат
{q, f} направлена в сторону внешней нормали к
апертуре. Сферические компоненты полного электрического поля в
дальней зоне могут быть представлены в следующем виде:
|
|
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
|
(1 + cosq)
4
|
e- i f(Ney-Nmx - i Nex- iNmy) + |
| |
|
ж
з
и
|
|
| |
ц
ч
ш
|
|
(1 - cosq)
4
|
ei f( Ney + Nmx +i Nex - i Nmy) + |
| |
|
ж
з
и
|
|
| |
ц
ч
ш
|
|
(1 + cosq)
4
|
e i f(Ney - Nmx +i Nex + i Nmy) + |
| |
ж
з
и
|
|
| |
ц
ч
ш
|
|
(1 - cosq)
4
|
e-i f( Ney + Nmx -i Nex + i Nmy) |
| (22) |
| |
|
Здесь введено обозначение
{Nex, Ney, Nmx, Nmy} для диаграмм направленности от
отдельных декартовых составляющих электрических и магнитных
плотностей токов в плоскости апертуры.
|
|
| = - |
i k
4 p
|
|
e-i k R
R
|
|
у
х
|
|
у
х
|
A
|
|
| ei k sinq(x cosf+ y sinf)dx dy, |
| (23) |
В выражении (22) поле каждой круговой поляризации
представлено в виде суммы двух слагаемых, одно из которых
соответствует сумме элементов Гюйгенса, излучающих кардиоидную
диаграмму направленности с максимумом в главном направлении, а
другое - сумме элементов Гюйгенса с кардиоидой противоположного
направления. Заметим, что излучение каждого из названных типов
элементов Гюйгенса, независимо от направления максимального
излучения, идеально поляризовано по кругу соотвествующего
направления вращения.
В теории зеркальных антенн распределение
поля по апертуре часто рассчитывается в геометрооптическом
приближении по известной диаграмме направленности облучателя.
Если плоскость апертуры совпадает с геометрооптическим волновым
фронтом, то в этом случае составляющие, соответствующие
элементам Гюйгенса с нулевым излучением в главном направлении, в
апертурном распределении отсутствуют. Эти составляющие имеют
дифракционное происхождение.
4.2 Источники излучения антенны в базисе
линейной поляризации
Приведем разложение поля излучения антенны в дальней зоне в
апертурном приближении, аналогичное разложению (22) и
удобное для анализа поляризационной структуры в базисе линейных
поляризаций. Будем считать, что базисные линейные поляризации
параллельны осям X и Y декартовой системы координат в
плоскости апертуры (плоскостям f = 0 и f = p/2,
соответственно), причём, поляризацию электрического вектора вдоль
оси Y будем считать согласованной, а вдоль оси X -
кроссполяризованной. Сферические компоненты полного
электрического поля в дальней зоне могут быть представлены в
следующем виде:
|
|
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
(1+cosq)
2
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
(Ney - Nmx) + |
| |
|
(1-cosq)
2
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
(Ney + Nmx) + |
| |
|
(1+cosq)
2
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
(Nex + Nmy) + |
| |
(1-cosq)
2
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
(Nex - Nmy) |
| (24) |
| |
|
Обозначения те же, что и в формуле (22).
Первые два слагаемых в формуле (24)
определяют поле, возбуждённое
составляющими источников согласованной поляризации {Jey,Jmx}, последующие два слагаемых - поле, возбуждённое
составляющими кроссполяризованных источников {Jex, Jmy}.
Первое и третье слагаемые соответствуют совокупности элементов
Гюйгенса с максимумом излучения в сторону внешней нормали к
апертуре (множитель (1+cosq)), второе и четвертое
слагаемые соответствуют элементам Гюйгенса,
направленным в противоположную сторону (множитель
(1-cosq)). Излучение элементов Гюйгенса с множителем
направленности (1+cosq), в соответствии с разложением
(3), имеет постоянную поляризацию в пространстве
относительно рассматриваемой системы координат, тогда как
элементы Гюйгенса с нулем кардиоиды в главном направлении, в
отличие от аналогично направленных элементов Гюйгенса,
поляризованных по кругу, имеют переменную линейную поляризацию.
Эта ситуация иллюстрируется
изображённой на рис.
1
сферой
с нанесенными на ней линиями постоянных направлений поляризации
линейно поляризованного источника Гюйгенса.
Необходимыми и достаточными условиями
идеальной линейной поляризованности апертурной антенны является
обращение в нуль излучения элементов Гюйгенса, направленных в
сторону внешней нормали, возбужденных кроссполяризованными токами
(z0 Jex + Jmy), и кроме того, следующее алгебраическое
соотношение между диаграммами направленности элементов Гюйгенса,
направленных внутрь апертуры:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
F(q, f), |
| (25) |
где F(q, f) -
произвольная скалярная диаграмма направленности.
Из выражени
(25) следует, что излучение антенны идеальной
линейной поляризации может создаваться не только
кополяризованными токами в апертуре, но и кроссполяризованными.
Если же плоскость апертуры совпадает с геометрооптическим
волновым фронтом, то в апертурном распределении, рассчитаном в
геометрооптическом приближении, отсутствуют составляющие,
соответствующие элементам Гюйгенса, направленным внутрь апертуры.
Источники такой идеально поляризованной антенны могут
быть только кополяризованными.
5 Кроссполяризация, обусловленная отражением
5.1 Кроссполяризация при отражении от криволинейной
идеально проводящей поверхности
Кроссполяризация из-за наклона оси
облучателя к оси зеркала.
Если облучатель идеально поляризован в сферической системе
координат, полярная ось которой является осью симметрии
зеркальной антенной системы, диаграмма направленности зеркальной
системы, рассчитанная по геометрооптическому апертурному
распределению, также будет свободна от кроссполяризации в
рассматриваемой системе координат. Отсутствие кроссполяризации
связано только с соосностью зеркальной системы и
(идеально поляризованного) облучателя, и будет иметь место даже
в случае соосного облучения несимметричной вырезки из
параболоида. Однако такое облучение несимметричной вырезки
обычно не применяется из-за больших потерь на переоблучение
зеркальной системы. Для уменьшения потерь, ось облучателя,
нарушая симметрию, смещают к центру вырезки. Рассмотрим
возникающие при этом эффекты.
Будем предполагать, что сфокусированная вырезка из
осесимметричной зеркальной системы облучается идеально
линейно поляризованным облучателем,
повернутым в плоскости симметрии зеркал(а) на
угол q0, как показано на рис.
5.
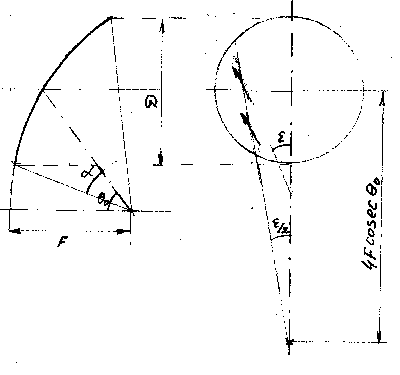 Рис5.
Рис5.
Поляризация поля в апертуре параболического зеркала
при несимметричном облучении поляризационно-чистым
облучателем.
Геометрия вырезки из параболы с точностью до подобия
может быть определена заданием двух углов: угла a
раскрыва конуса облучения вырезки и угла q0 отклонения
оси облучателя от фокальной оси параболоида. Пусть облучатель
поляризован в плоскости симметрии, совпадающей с плоскостью Y0Z.
Его диаграмма направленности в повернутой системе координат
определяется выражением:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
Fy(q, f) |
| (26) |
Перейдём к сферической системе координат, полярная ось которой
совпадает с осью симметрии зеркальной системы. Выражение для
диаграммы направленности в новом базисе линейных поляризаций
примет вид:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= { |
ж
з
и
|
|
| |
ц
ч
ш
|
cose- |
ж
з
и
|
|
| |
ц
ч
ш
|
sine} Fy(q,f) |
| (27) |
Первое слагаемое в фигурных скобках соответствует
кополяризованной части, второе слагаемое -
кроссполяризованной. Все переменные в приведенной формуле должны
быть выражены через штрихованные переменные {qў,fў}
относительно оси симметрии системы. В
плоскости апертуры зеркальной системы, ортогональной оси
симметрии, можно перейти к полярным координатам {r, fў} с
началом на оси симметрии, причём, переменная qў
выражается через r по законам геометрической оптики, например,
для случая параболического зеркала по формуле:
где F -
фокусное расстояние зеркала. В результате излучающие
электрические и магнитные токи в апертуре можно определить по
формулам:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
Fy(q,f) |
| (29) |
В плоскости апертуры направление излучающих токов, возбуждённых
повёрнутым относительно оси зеркала идеально поляризованным
облучателем, поворачивается на угол e и, тем самым,
создаёт эффект кроссполяризации.
На рис.
5
в плоскости апертуры несимметричного параболоида
показаны линии постоянного направления излучающих токов.
Линии являются прямыми и пересекаются в точке, расположенной в
плоскости симметрии на расстоянии 4 F/sinq0 от
центра круговой апертуры. Излучающие токи направлены под углом к
линиям постоянного направления, так что угол отклонения токов
вдвое превышает угол отклонения линий.
Величина кроссполяризационной ошибки пропорциональна среднему
квадрату синуса углового избытка в телесном угле диаграммы
направленности облучателя в направлении на зеркало. Так как
угловой избыток пропорционален площади сферического треугольника,
а площадь увеличивается с увеличением угла облучения рефлектора,
или, что то же самое, с уменьшением фокусного расстояния, то в
этом же случае возрастает кроссполяризационная ошибка.
При облучении зеркала радиоволной круговой поляризации эффект
кроссполяризации при расчете отраженного от зеркала
поля в геометрооптическом приближении исчезает, но вместо него из-за
фазового множителя eie с фазой, меняющей знак при
переходе через плоскость симметрии, возникает смещение максимума
диаграммы направленности антенны в направлении перпендикулярном
плоскости симметрии. Смещение максимума диаграммы направленности
для различных направлений вращения поляризации происходит в
противоположные стороны. Главный член величины смещения можно
оценить по формуле:
|
Dq = |
й
к
л
|
|
1+1.5 D
1+D
|
|
16
15(1+(4 F /D)2)
|
|
щ
ъ
ы
|
|
l
pD
|
|
| (30) |
В этой формуле:
D - диаметр апертуры,
F - фокусное расстояние
параболоида,
D - относительный уровень облучения края
апертуры по полю.
Предполагается, что выполнено
геометрическое соотношение a = q0, а распределение
поля по апертуре осесимметричное, определяется параболическим
законом
|
f(r) = 1-(1-D)r2, 0 < r < 1. |
|
На рис.
6
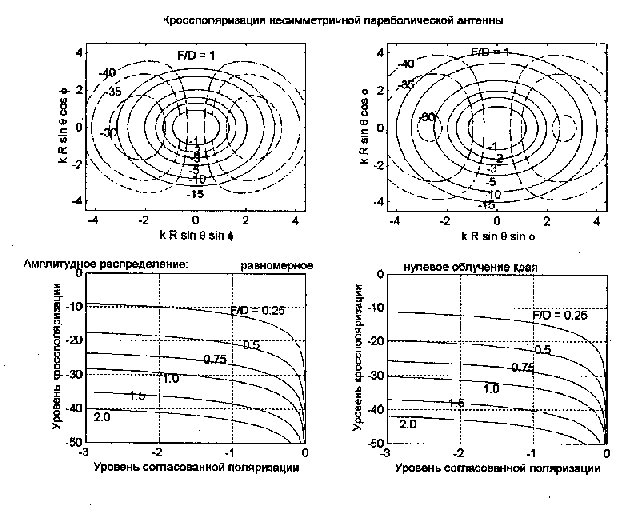
Рис6. Эффекты кроссполяризации для однозеркальной
параболической вырезки.
показаны
зависимости кроссполяризационной ошибки при линейно
поляризованном облучении однозеркальной антенны типа
несимметричной вырезки из параболы от геометрических параметров
антенны. Предположения те же, что и выше.
Результаты,
показанные на рисунках слева, соответствуют равномерному
облучению апертуры, справа - распределению амплитуды, спадающему
по параболическому закону от центра к краям до нуля. На верхних
рисунках показана топография ко- и кроссполяризованных диаграмм
направленности в области главного лепестка для фокального
отношения антенны F/D = 1. На нижних рисунках -
распределение максимального уровня кроссполяризации в областях с
заданным снижением уровня согласованной поляризации при различных
значениях F/D. Кроссполяризованное излучение, хотя и
уменьшается при уменьшении уровня облучения края апертуры, но,
как видно из нижних рисунков, это уменьшение несущественно.
Можно ли скомпенсировать кроссполяризацию, возникшую из-за
несовпадения осей облучателя и зеркала?
В ряде работ предложены конструкции облучателя, создающего
излучение, компенсирующее кроссполяризационные эффекты
однозеркальных несимметричных параболоидов [8],
[6]. В качестве таких облучателей рассматривались
двухмодовые гофрированные рупоры (с волнами HE11 и
HE21), гладкие рупоры с изломами образующей (с волнами
H11, E11, H21) и решетки облучателей.
Для случая двух- или многозеркальных устройств, образованных
поверхностями вращения второго порядка, метод
геометрооптической компенсации кроссполяризации
может быть основан на следующем утверждении:
Пусть такая поверхность облучается из фокуса,
причём, кроссполяризация облучателя отсутствует в сферической
системе координат с полярной осью, отклонённой от оси поверхности
(гиперболоида или эллипсоида) на угол y0. Тогда
кроссполяризация отражённого поля отсутствует в сферической
системе координат с полюсом во втором фокусе и полярной осью,
отклонённой от оси отражающей поверхности второго порядка на угол
a, определяемый формулой:
|
|
ctg
| |
a
2
|
= |
e+1
|e-1|
|
|
ctg
| |
y0
2
|
|
| (31) |
где e - эксцентриситет гиперболы или эллипса, а
положительные направления отсчета углов показаны на
рис.
7.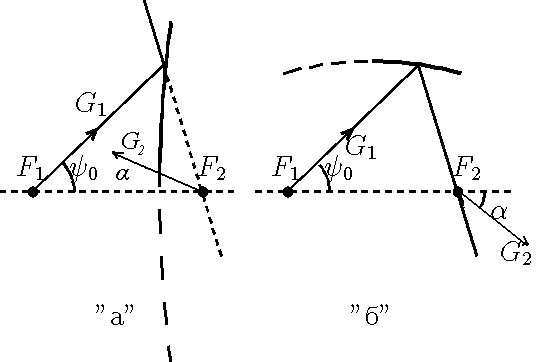
Рис7. Угловое положение осей сферических систем
координат, в которых падающая и отражённая от
поверхности вращения 2-го порядка диаграммы
направленности идеально поляризованы,
"а" - отражение от гиперболоида,
"б" - отражение от эллипсоида.
Соотношения (31)
непосредственно следуют из сопоставления выражения для углового
избытка (11) и формулы, связывающей углы наклона лучей,
соединяющих произвольную точку на гиперболе или эллипсе с
фокусами.
Геометрические соотношения для несимметричной, "дважды смещенной"
антенны Кассегрена или Грегори с компенсированной
кроссполяризацией следуют из данного утверждения, когда
фокус параболоида совмещен с фокусом отражённой волны, а ось
параболоида направлена под углом a к оси гиперболоида или
эллипсоида, как показано на рис.
8.
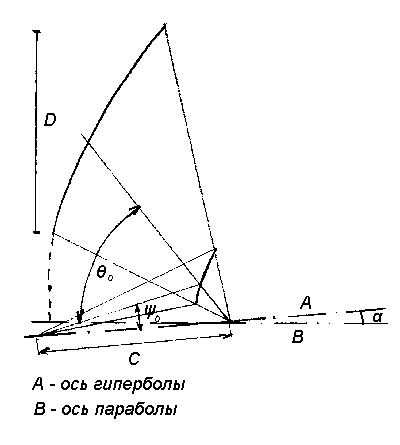 Рис8.
Рис8. Геометрия несимметричной двухзеркальной антенны.
Соотношени
между этими углами, эквивалентные формуле (31), получены
в [15].
Условие геометрооптической компенсации кроссполяризации
при последовательном отражении от двух несимметричных
поверхностей второго порядка получено в работе [16] (см.
также обзор [17]). Отражающие поверхности второго
порядка с фокусами {F1, F2, F3, F4}, два из которых,
относящиеся к различным поверхностям, совпадают (F2 = F3),
облучаются осесимметричным поляризационно чистым облучателем,с
фазовым центром в фокусе F1, и осью, наклонённой к линии
фокусов облучаемого зеркала. Достаточные условия компенсации
кроссполяризации следующие:
- фокусы отражающих зеркал находятся на одной прямой,
- эксцентриситеты зеркал равны или обратно
пропорциональны.
При этих условиях, в отличие от общего случая, определяемого
формулами (31), амплитудная диаграмма направленности
выходного дважды отражённого пучка та же, что и входного.
Системы из нескольких несимметричных зеркал используются в
технике зеркальных антенн в конструкциях лучеводов. Четыре
варианта лучеводов с компенсированной кроссполяризацией,
предложенные в [16] показаны на рис.
9.
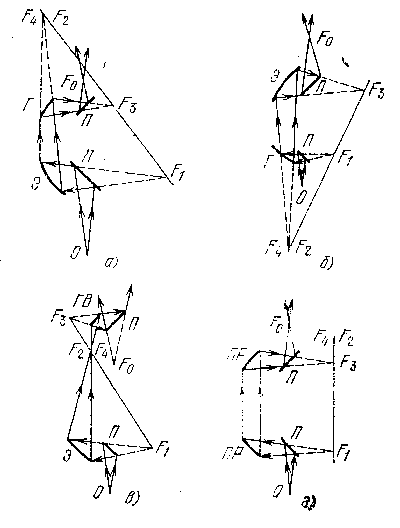
Рис9. Компенсация кроссполяризации при последовательных
отражениях от поверхностей 2-го порядка.
Расчет поляризационных характеристик лучевода более общего вида,
состоящего из произвольного количества несимметричных вырезок
поверхностей второго порядка, в приближениях геометрической
оптики и гауссовых пучков представлен в монографии
[4].
Если зеркальная система не
является вырезкой из осесимметричной, эффекты
кроссполяризации сфокусированных несимметричных зеркальных систем
можно вывести из условия конформности геометрооптической
трансформации сферической области определения диаграммы
направленности облучателя в плоскую область апертуры главного
рефлектора. Пусть диаграмма направленности осесимметричного
облучателя определена в сферической области с координатами
q, f, а распределение поля по апертуре рефлектора
описывается в координатах x, y. Не ограничивая общности будем
предполагать что диаграмма направленности линейно поляризованного
облучателя без кроссполяризации, удовлетворяющего критерию
(6), трансформируется по законам геометрической оптики в
распределение по апертуре, поляризованное преимущественно в
направлении y- оси. Пусть геометрооптическая трансформация
сферической области в апертуру описывается двумя функциями:
а диаграмма
направленности облучателя описывается выражениями:
|
Eq = f(q) sinf, Ef = f(q) cosf. |
|
Линии тока вектора E в области определения диаграммы
направленности облучателя на сфере определяются дифференциальным
уравнением:
|
|
d q
f(q) sinf
|
= |
sinqd f
f(q) cosf
|
, |
|
из которого следует, что
на линиях тока выполняется условие:
.
В апертуре рефлектора линии тока также переходят в линии тока
вектора электрического поля, наклон которых по отношению к оси
y определяется выражением:
Приведенное выражение может быть использовано для оценки
кроссполяризационных эффектов несимметричной зеркальной антенны с
модифицированными рефлекторами. Приравнивание нулю числителя
этого выражения определяет дифференциальное уравнение, которому
должна удовлетворять несимметричная зеркальная система, чтобы в
ней не появлялись кроссполяризационные эффекты. Дифференциальные
уравнения такого типа рассматривались в работах [18],
[19], в которых описаны методы расчета поляризационно
чистых двухзеркальных антенн. Для двухзеркальных антенн (в том
числе, с модифицированными профилями зеркал) обращение в нуль
числителя выражения (32) обеспечивает компенсацию
кроссполяризованных составляющих, возникающих в главном члене
высокочастотной асимптотики при отражении от зеркал.
Кроссполяризация во втором члене
асимптотики
В данном разделе исследован вариант возможности возникновения
кроссполяризации во втором члене высокочастотной асимптотики
в осесимметричном случае при отражении от криволинейного идеально
проводящего зеркала. Пусть поверхность осесимметричного зеркала в
сферической системе координат {r, q, f} описываетс
функцией r(q), а падающее поле правой круговой поляризации
функциями:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
vin0, vin0 = |
e-i k r
r
|
f(q, f), |
| (33) |
где f(q, f) - диаграмма направленности падающего
поля, вектор F+ связан с векторами
электромагнитного поля {E,H} формулой
(14).
Известно, что главный член высокочастотной
асимптотики отражённого поля
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= |
ж
з
и
|
|
| |
ц
ч
ш
|
uout0, uout0 = |
e-i k sout
r[Jout]1/2
|
f(q, f), |
| (34) |
имеет при этом левокруговую поляризацию. В приведенном выражении
q - угол отклонения падающего луча, переходящего в
рассматриваемый отражённый луч, r(q) - радиальная
координата зеркала в точке отражения,
sout, Jout - геометрооптический
эйконал и якобиан отражённой волны, {sout,b,f} образуют ортогональную осесимметричную лучевую систему
координат отражённого поля. Угол отражения b связан с углом
отклонения от оси системы падающей волны q по формуле
b = 2 a- q, где a - угол падения,
тангенс которого определяется выражением:
Нас интересует главный
член кроссполяризованной составляющей (в данном случае
правокруговой) отражённой волны.
Из высокочастотной асимптотики решения поставленной задачи можно
получить, что отношение амплитуд первой кроссполяризованной
составляющей к главному члену отражённой волны определяется
формулой:
|
|
vout1
uout0
|
= |
1
2 k r
|
|
ж
з
и
|
t |
ctg
| q- |
tў + t2
1+t2
|
|
ц
ч
ш
|
, |
| (36) |
в которой
в точке отражения и выражается
формулой (35).
Итак, уровень кроссполяризации определяется профилем поверхности
отражающего зеркала и обратно пропорционален (по полю) расстоянию
от облучателя до зеркала в длинах волн. На рис.
10
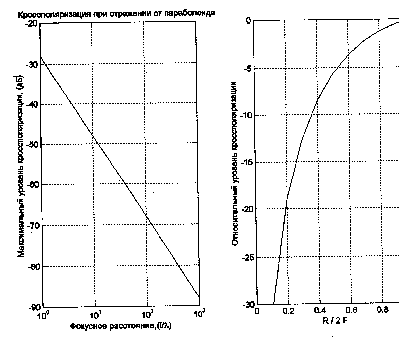
Рис10. Кроссполяризация во втором члене высокочастотной
асимптотики при облучении симметричного параболоида.
приведены результаты расчета уровня
кроссполяризации, возникающей при отражении от осесимметричного
параболоида, облучаемого поляризационно чистым облучателем
круговой поляризации. Распределение уровня кроссполяризованного
излучения по отношению к кополяризованному складывается из двух
составляющих: одного, определяемого фокусным расстоянием
параболоида (заданным в длинах волн), и другого, определяемого
распределением кроссполяризации по апертуре параболоида. На
рис.
11
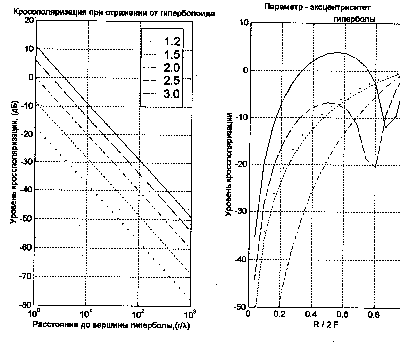
Рис11. Кроссполяризация во втором члене высокочастотной
асимптотики при облучении симметричного гиперболоида.
приведены аналогичные результаты
для поля, отраженного от гиперболоида. В этом случае уровень
кроссполяризации также можно представить в виде суммы двух
слагаемых, одного, зависящего от расстояния от облучателя до
вершины, и другого, распределенного по отражённой диаграмме
направленности и зависящего также от эксцентриситета гиперболы.
Существенный уровень кроссполяризации соответствует низкому
значению эксцентриситета и большому углу отражения, то есть
глубокому главному зеркалу.
Приравнивание нулю выражения (36)
приводит к дифференциальному уравнению, определяющему профиль
рефлектора, отражённая волна от которого не содержит
кроссполяризованной составляющей в нулевом и первом членах
высокочастотной асимптотики. Решение этого дифференциального
уравнения дает двухпараметрическое семейство профилей. В
качестве параметров можно выбрать r0 - расстояние от фазового
центра облучателя до вершины рефлектора и R0 - радиус кривизны
рефлектора в вершине. Профиль такого рефлектора в полярных
координатах относительно фазового центра облучателя дается
следующим разложением:
|
| |
|
|
| (37) | |
|
|
|
p q2
2
|
+ |
pq4
4
|
(- |
1
6
|
- |
p
2
|
+ |
p2
2
|
) + |
pq6
6
|
( |
1
120
|
+ |
p
8
|
- |
5 p3
8
|
+ |
3 p4
8
|
) + |
| |
|
|
pq8
8
|
(- |
1
5040
|
- |
p
80
|
- |
7p2
240
|
+ |
p3
4
|
+ |
11 p4
48
|
- |
35p5
48
|
+ |
5p6
16
|
) + O(q10) , |
|
| |
|
в котором p = 1+[(r0)/( R0)] и
положительный знак радиуса кривизны соответствует рефлектору,
обращённому выпуклостью к облучателю.
5.2 Кроссполяризационные потери в главном члене
высокочастотной асимптотики при отражении от импедансной
поверхности
Анизотропные импедансные поверхности используются в
конструкции облучателей для уменьшения кросссполяризационного
излучения. При электродинамическом анализе импедансные
поверхности рассматриваются как "локально
реагирующие" [20], для нахождения отражённого от них
поля используются импедансные граничные условия
М.А.Леонтовича, которые имеют вид:
|
[n, E] = Z [n, [ n, H] ], |
| (38) |
здесь n - единичная нормаль к
поверхности, направленная внутрь среды, в которой определяется
поле, Z - тензор, вообще говоря анизотропного, импеданса
поверхности.
Главный член высокочастотной асимптотики отражённого поля
определяется решением задачи о падении плоской волны на
анизотропную плоскость. Если рассматривается случай падения
плоской волны круговой поляризации с углом падения a, то
для коэффициентов отражения плоских волн согласованной и
ортогональной круговых поляризаций справедливы следующие
выражения:
|
| |
|
|
|
|
z0 ( z11 cosa- z22 seca+ iz12 +i z21 )
|
z02 + z0 ( z11 cosa+ z22seca) + |
det
| Z |
|
|
| |
|
|
|
z02 + iz0 ( z21 - z12) - |
det
| Z |
|
z02 + z0 ( z11 cosa+ z22 seca) + |
det
| Z |
|
|
| (39) |
| |
|
Здесь z0 - волновой импеданс
свободного пространства.
При Z = 0, то есть при падении на идеально
проводящую плоскость, кополяризованная волна отсутствует, а
амплитуда кроссполяризованной волны равна амплитуде падающей.
Для случая скалярного импеданса отражающей поверхности
(поверхности с конечной проводимостью или границы диэлектрика в
случае, когда могут быть применены условия Леонтовича,) амплитуды
ко- и кроссполяризованной отражённых волн даются выражениями:
|
pco = |
- z0 z sin2 a
(z0+zcosa) ( z0 cosa+ z)
|
, pcr = |
z02-z2
(z0+z cosa) ( z0 cosa+ z)
|
|
| (40) |
Если z № 0, то в отличие от
идеально проводящей поверхности при косом падении в главном
геометрооптическом члене возникает кополяризованная отражённая
волна но, естественно, при нормальном падении она равна нулю. В
этом случае кополяризованная волна создаёт эффект паразитной
поляризации, например, от влияния покрытия зеркал или атмосферных
осадков.
Для случая, когда импедансная поверхность обладает свойством
взаимности z12 = z21, кроссполяризованная
волна полностью отсутствует при выполнении условия:
|
|
det
| Z = z11 z22 -z122 = z02. |
| (41) |
Выполнение этого условия не
зависит ни от угла падения волны, ни от ориентации анизотропной
плоскости. Данное свойство было впервые использовано Кэем при
создании так называемого "скалярного рупора" в 1964г. и
очень широко используется вплоть до настоящего времени.
Чтобы потери энергии при отражении были
равны нулю, импеданс отражающей поверхности должен быть
реактивным. Условие отсутствия кроссполяризованной отражённой
волны для этого случая называется "условием симметрии поля
гибридных волн":
здесь x1 и x2 - реактивные импедансы
анизотропной плоскости в главных направлениях.
Анизотропные импедансные поверхности используются и
для других целей, например, для преобразования поляризации
круговой в линейную и наоборот. Однако в этом случае
поляризационные свойства зависят как от угла падения, так и от
ориентации анизотропной плоскости относительно плоскости падения.
Для описания поляризационных свойств реактивной анизотропной
поверхности необходимо в формулу (39) вместо компонент
zij подставить выражение тензора
импеданса в зависимости от ориентации анизотропной
поверхности относительно плоскости падения волны:
В этом выражении f -
угол наклона плоскости падения волны к главной плоскости сечения
анизотропной поверхности, а z1 и z2 - главные
импедансы поверхности.
С учетом этого ко- и кроссполяризационные компоненты волны,
отражённой от реактивной анизотропной поверхности, полностью
описываются следующими выражениями:
|
| |
|
|
(x2 - x1) sin2 f- |
i
2
|
(x2 -x1) (seca+ cosa) cos2 f- |
| |
|
|
i
2
|
(x2 + x1) (seca- cosa) , |
| |
| |
|
z02 - x1 x2 +z0 ( |
i
2
|
(x2 + x1) (seca+ cosa) - |
| |
|
i
2
|
(x2 - x1) (seca- cosa) cos2 f), |
|
| |
|
|
pco = |
z0 A
C
|
, pcr = |
B
C
|
, |
| (44) |
где x1 и x2 - главные
реактивные импедансы поверхности в точке отражения.
Дополнительное ограничение на импеданс анизотропной плоскости
накладывается условием недопустимости поддержания поверхностной
волны. Как известно [21], поверхностная волна
поддерживается, если в плоскости падения волны
импеданс индуктивный (возникает E-поляризованная поверхностная
волна) , либо в ортогональной плоскости
емкостной (в этом случае возникает H- поляризованная
поверхностная волна). В круглом ребристом рупоре с первой
азимутальной гармоникой плоскость падения волны, определяемая в
соотвествии с концепцией Бриллюэна, практически совпадает с
меридиональной плоскостью, поэтому, чтобы не допустить
возможности распространения поверхностной волны, импеданс,
удовлетворяющий условию (42), в меридиональной
плоскости должен быть емкостным, а в азимутальной плоскости
индуктивным.
В антенной практике нашли широкое применение облучатели в виде
гофрированных рупоров с канавками, прорезанными в
азимутальном направлении, а также в виде открытых концов
круглого волновода с гофрированным фланцем. Глубина
канавок h немного больше четверти длины волны, а период гофра
менее половины длины волны. Импеданс такой поверхности в
меридиональной плоскости емкостной, достаточно большой величины,
а в азимутальной - индуктивный, близкий к нулю. Поверхностная
волна не поддерживается. Кроссполяризационные свойства
гофрированных рупоров и других облучателей зеркальных
антенн описаны в работах [22], [23].
6 Влияние кроссполяризации
облучателя зеркальной антенны
Кроссполяризационное излучение в диаграмме направленности
облучателя зеркальной антенны складывается из составляющих,
вызванных неидеальностью элементов фидерного тракта (поляризатора
или мостового устройства), и неидеальностью конструкции
самого облучателя, приводящей, например, к отличию
диаграмм направленности в Е- и Н- плоскостях. Не останавливаясь
на первой причине, которая легко анализируется, рассмотрим вторую
составляющую для случая соосного облучения осесимметричной
зеркальной системы облучателем, не удовлетворяющим критерию
(6). Кроссполяризационные характеристики облучателя
осесимметричной зеркальной антенны, измеренные в сферической
системе координат, соосной с зеркальной системой,
трансформируются в соответствующие характеристики всей антенны.
Диаграмма направленности облучателя,
возбужденного в режиме правой круговой поляризации, может быть
представлена в следующем виде:
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
= e-if |
ж
з
и
|
|
ж
з
и
|
|
| |
ц
ч
ш
|
fco(q) + |
ж
з
и
|
|
| |
ц
ч
ш
|
e2 i f fcr(q) |
ц
ч
ш
|
, |
| (45) |
fco(q) - диаграмма направленности облучателя по
согласованной поляризации, fcr(q) - по паразитной. В
качестве математической модели облучателя в теории зеркальных
антенн полезно использование "скалярного рупора", который
можно представить в виде круглой апертуры, с амплитудным
распределением поля в виде функции Бесселя нулевого порядка,
спадающей на краю апертуры до нуля. Такой вид имеет
поперечное распределение волны основного типа в гофрированном
волноводе, в котором может распространяться волна без
кроссполяризации.
|
fco(q) = |
у
х
|
1
0
|
J0(c1 t) J0(t k a sinq) t dt = c0 |
J0(k a sinq)
1 - (k a sinq/ c1)2
|
|
| (46) |
Кроссполяризованная диаграмма направленности возбуждается
аналогичным распределением в виде функции Бесселя второго
порядка:
|
| |
|
|
|
|
у
х
|
1
0
|
J2(c1 t) J2(t k a sinq) tdt |
| |
|
| c0 |
ж
з
и
|
|
J0(k a sinq)
1 - (k a sinq/ c1)2
|
- |
2 J1(k a sinq)
k a sinq
|
|
ц
ч
ш
|
|
| (47) |
| |
|
Амплитуда возбуждения кроссполяризованной
волны определяется погрешностями в конструкции или настройке
облучателя. При ненулевой амплитуде кроссполяризованной волны
суммарная диаграмма направленности не осесимметрична, можно найти
две ортогональные плоскости, в одной из которых диаграмма
направленности будет самой узкой, а в другой самой широкой.
Уровень кроссполяризации облучателя, а следовательно и зеркала,
определяется различием этих диаграмм направленности, для
определённости, например, в области, где средняя диаграмма
направленности спадает до уровня минус 3 дБ.
Каждая из поляризационных составляющих трансформируется в
осесимметричной зеркальной системе независимо. Рассмотрим случай
однозеркальной параболической антенны. Полученный результат без
изменения справедлив и для двухзеркальных антенн Кассегрена
или Грегори. Рассчитанные
кроссполяризационные характеристики зеркальной
системы, у которой край параболического
рефлектора (гиперболического или эллиптического контррефлектора)
облучается по уровню минус 10 дБ,
представлены на рис.
12.
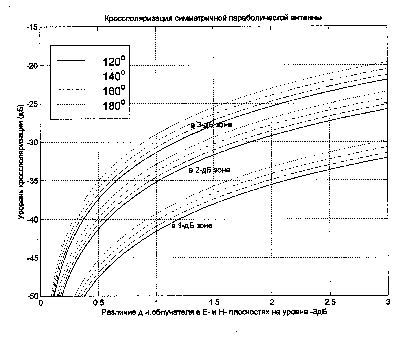
Рис12.
Эффекты кросполяризации осесимметричной
параболической антенны, вызванные кроссполяризацией
облучателя.
По оси абсцисс отложена максимальная несимметрия диаграммы
направленности облучателя в двух ортогональных плоскостях по
уровню минус 3 дБ. (Для случая линейного облучателя - это
различие диаграмм направленности в Е- и Н- плоскостях.) По оси
ординат отложено максимальное значение уровня кроссполяризации
зеркальной системы в областях диаграммы направленности,
ограниченных линиями уровня средней диаграммы направленности
-1, -2 и -3 дБ. Кривые разного вида на рис.
12
- сплошные, пунктирные и т.д., соответствуют различным углам
облучения главного рефлектора (от 120o до 180o ). Из
представленных материалов следует, что результирующий уровень
кроссполяризации в большей мере определяется зоной диаграммы
направленности, чем фокальным отношением рефлектора. Для
осесимметричной диаграммы направленности облучателя,
удовлетворяющей критерию (6), кроссполяризация
зеркальной системы полностью отсутствует, независимо от
фокального отношения рефлектора. При построении кривых
рис.
12
использованы предположения, которые могут не
осуществиться на практике, - это предположение о синфазности ко-
и кроссполяризованных диаграмм направленности fco(q) и
fcr(q) и о синфазности распределения поля в апертуре
рупора. Представление о характере зависимости уровня
кроссполяризации от фазовых соотношений ко- и кроссполяризованных
диаграмм можно получить из рис.
%3
7 Заключение
Кроссполяризация зеркальной антенны линейной поляризации
возникает из-за отклонения вектора поляризации в диаграмме
направленности антенны от вектора поляризации референсного
линейно поляризованного источника Гюйгенса.
В данной статье кроссполяризация представлена как
результат влияния отдельных независимых источников: собственной
кроссполяризации облучателя, отклонения осей облучателя и
параболического зеркала, несимметрии зеркальной системы.
Результаты данной статьи могут быть использованы и для
оценки совместного влияния рассматриваемых источников
кроссполяризации, определяеющегося алгебраической суммой углов
отклонения векторов поляризации в каждом направлении диаграммы
направленности. При этом может произойти смещение максимума
кроссполяризации в диаграмме направленности и изменение
максимального уровня. В том случае, когда в несимметричной
зеркальной системе выполняется геометрооптическое условие
отсутствия кроссполяризации, результирующая кроссполяризация
определяется совместным влиянием собственной кроссполяризации
облучателя и дифракционными эффектами на кромке вспомогательного
зеркала, которые рассмотрены в ряде работ, цитированных в
[24].
В зеркальных антеннах круговой поляризации рассматриваемые
источники не всегда вызывают кроссполяризацию, но их влияние
приводит к нежелательным искажениям формы диаграммы
направленности. В то же время, выполнение
геометрооптических условий отсутствия кроссполяризации в
несимметричной зеркальной антенне приводит одновременно к
устранению (в геометрооптическом приближении) несимметричных
искажений диаграммы направленности, когда эта антенна облучается
облучателем круговой поляризации.
Список литературы
- [1]
- Рекомендации и отчеты МККР, 1986г.,
Отчёт 390-5. Антенны земных станций фиксированной спутниковой
службы.
- [2]
- Г.Т.Марков, Д.М.Сазонов
Антенны: Учебник для вузов. - 2-е изд. - М.: Энергия, 1975г.
- [3]
- П.Вуд Анализ и проектирование зеркальных
антенн, перевод с англ. Г.Б.Звороно, под ред.
О.П.Фролова, М., Радио и связь, 1984
- [4]
-
Advanced Technology in Satellite Communication Antennas.
Electrical and Mechanical Design. Takashi Kitsuregawa,
Editor. 1990.
- [5]
-
Reflector Antennas,
/Ed: A.W.Love/, New-York, IEEE Press, 1978
- [6]
- Antenna Handbook: theory, applications, and
design.
/Ed: Y.T.Lo, S.W.Lee/ New-York, 1988
- [7]
-
В.П.Нарбут, В.Ф.Хмель
Поляризация излучения зеркальных антенн.
Головное издательство издательского объединения "Вища
школа", Киев, 1978
- [8]
-
Alan W. Rudge, Nurdin A. Adatia
Offset-Parabolic-Reflector Antennas: A Review,
Proc.IEEE, v.66, n.12, pp.1592-1612, Dec., 1978
(перевод: ТИИЭР, т.66, №12, декабрь, 1978)
- [9]
- Arthur C. Ludwig The Definition of Cross
Polarization. IEEE Trans. Antennas Propagat.,vol. AP-21, pp.
116-119, Jan.,1973.
- [10]
- Методы измерения характеристик антенн СВЧ.
Под редакцией Н.М.Цейтлина. - М: Радио и связь, 1985г.
- [11]
-
Волынский Б.А.
Сферическая тригонометрия.
Наука, ГРФ-МЛ, М, 1977
- [12]
-
Rumsey V.H. Частотно независимые антенны. -
В кн.: Сверхширокополосные антенны. М., " Мир", 1964, с.11.
- [13]
-
Г.Т.Марков
Антенны. М., Госэнергоиздат, 1960г.
- [14]
-
Сакс Р.С. О краевых задачах для системы
rot u + lu = h
Доклады АН СССР, т.199, 5, 1971г., с.1022 - 1025
- [15]
-
H.Tanaka, M.Mizusawa
Elimination of cross-polarisation in offset dual reflector
antennas,
Elec.Commun. (Japan) v.58, pp.71-78, 1975
- [16]
-
Mizusawa M., Kitsuregawa T.
A Beam Waveguide Feed Having a Symmetric Beam for Cassegrain
Antenna,
Inter. IEEE AP-S Symp. Dig., 1972, pp.319-321,
IEEE Trans., 1973, v.AP-21, № 6.
- [17]
- А.Я.Мирошниченко
Лучеводы для двухзеркальных антенн. Зарубежная
радиоэлектроника, № 7, 1981, с.28 - 62.
- [18]
- Б.Е.Кинбер
Обратные задачи теории зеркальных антенн - приближение
геометорической оптики., ИРЕ, препринт № 38 (410), Москва - 1984
- [19]
- B.S.Westcott, F. Brickell Dual offset
reflectors shaped for zero cross-polarisation and prescribed
illumination, J.Phys.. D:Appl.Phys.12, 169-186, 1979
- [20]
- Л.М.Бреховских Волны в слоистых
средах, НАУКА,М.,1973
- [21]
- Г.Т.Марков, А.Ф.Чаплин
Возбуждение электромагнитных волн Энергия , 1967г.
- [22]
-
A.F.Kay
The scalar feed US. Air Force Cambridge Research
Laboratory Rep. 62-347, March, 1964
- [23]
-
Microwave horns and feeds.
A.D.Olver, P.J.B.Claricoats, A.A.Kishk, L.Shafai,
New-York, IEEE press, 1994
- [24]
-
The handbook of antenna design., vol.1 and 2, ed.:
A.W.Rudge, K.Milne, A.D.Olver, P.Knight, 1988, P.Peregrinus
Lmt. on behalf of the IEE.
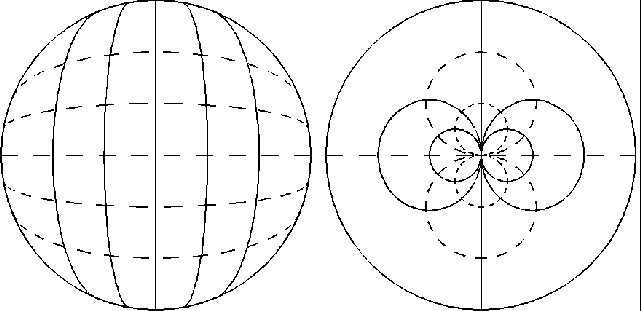 Рис1.
Рис1.
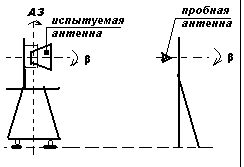 Рис2. Измерительная антенная установка.
Рис2. Измерительная антенная установка.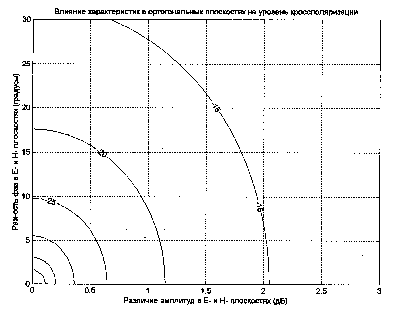 Рис3.
Рис3.
 Рис4
.
Рис4
. Рис5.
Рис5.

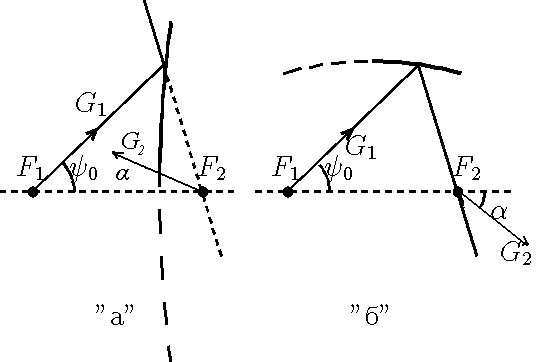
 Рис8.
Рис8.